带着问题，课堂撸“串”——问题串在初中数学课堂的应用探究

江苏省宜兴市西渚中学 羊文辉

所谓“问题串”，即老师紧密结合数学课程的教学内容，始终遵循“由浅入深、由表及里”的原则，合理设计一连串的数学问题，帮助学生在探究的过程中深入理解数学知识。本文将结合实际，就“问题串”教学策略于初中数学教学中的运用予以详细探讨。

一、设计新旧相关问题串，促使学生理解

数学各大知识点之间既存在着明显的区别，又存在着联系。教师在教授新知识的时候，可从旧知识入手，让学生根据所学的旧知识来理解新知识，这样不但有利于帮助学生深入理解数学知识，而且还能够提升学生的数学素养。

例如，针对“相似三角形性质”的相关内容教学，如果老师引入其他知识点来展开教学，则会增加学生对该数学知识点的理解，所以老师可从全等三角形的概念入手，并结合学生所学的知识点来设计“问题串”，降低数学知识点的难度，帮助学生深入理解相似三角形的概念，有效提升学生的数学思考深度。如问题一：全等三角形对应边及对应角之间分别存在怎样的数量关系？问题2：相似三角形的对应边及对应角之间分别存在怎样的数量关系？问题3：全等三角形周长及面积之间分别有着怎样的数量关系？问题4：相似三角形周长及面积之间分别有着怎样的对应关系？通过对以上问题进行深入探究，并利用问题来对比两部分之间的差异与联系，这样学生能够更准确地理解相似三角形的性质，掌握相似三角形对应边长度不相等但存在相同的比值的规律，有效提升初中学生的数学素养。

二、设计生活实际问题串，简化数学知识

数学知识虽然具有较强的抽象性，但其与实际生活之间的关联却尤为密切，在学生的日常生活中，随处可见数学的身影。因此，老师可紧密结合生活的实际情况设计问题串，这样学生便能够根据自身的生活经验理解数学知识点，有效降低学生学习数学的难度。同时，让学生感受到学习数学对实际生活的帮助，充分激发学生对数学学科的学习兴趣，有效提升初中学生的数学水平。当然，除了生活化元素的引进，教师亦立足于实际生活提出生活化的“问题串”，以此来强化学生对数学知识点的理解和掌握，逐步增强初中学生的数学能力。

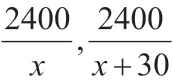
三、设计情境型问题串，激发学生探究欲望

数学概念是数学知识中非常重要的组成部分，但因内容相对枯燥，所以增加了学生对数学概念知识点的理解难度。因此，为深化学生对数学概念的理解，老师便可以创设良好的情景，并利用问题串来深入理解概念本质，促使学生准确理解数学知识点，有效提升学生的数学素养。

如针对“余角与补角”的相关内容教学，教师便可设置如下问题串：问题1：某人面前有两堵墙，墙面OA与OB之间形成了一个角∠AOB，对此，某人想测出两堵墙所形成的角度，但又不能进入墙内，请问其该如何进行测量？问题二：给予任意一个角度，请说出其的余角和补角。问题3：现已知∠AOB=180°，∠AOD=∠COE=90°，具体如图1 所示，问：∠3 的余角与补角分别为多少？问题4：已知图2 为3×3 的方格，试求∠1+∠2+∠3+∠4+∠5+∠6 的度数和。

概念教学是数学教学的重要内容，相对比较枯燥，教师更应该合理使用教材，创设合适情境，激发学生探究欲。通过设计问题串，突出概念的本质，能让学生对概念的理解在有效的问题串中自然达成。以《余角和补角》的教学为例，问题1：有两堵围墙OA、OB，有人想测量地面上所形成的角∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？问题2：任给一个角度，你能说出它的余角和补角吗？

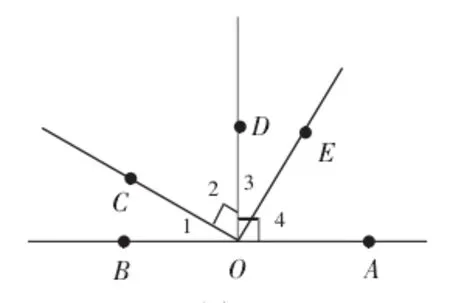
图1

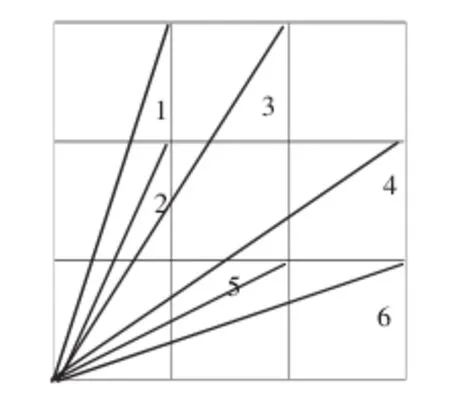
图2

评析：部分学生在思考以上问题时，其思维可能较为跳跃，故想到了坐飞机过墙或翻墙并直接测量的方式，但如此方式显然会让问题失去意义。因此，基于问题本身条件的限制，学生便想到了利用反向延长OA或OB的方式来得出补角与余角，至此，教师自然而然地便可引进补角与余角的概念。而基于问题2 的进一步深入，当学生考虑到此角为锐角时，其将抽象表达出∠x的余角（90°－∠x）及x的范围限制，当学生考虑到此点，其思维显然变得更加缜密。后在问题3、4 的激发下，学生将能明辨该概念，继而逐步产生学习的内在动力。

四、引入操作问题串，开拓学生数学思维

学生在学习过程中亦将不断发展，故在实际教学过程中，教师应务必致力于对学生综合能力的有效培养。对此，教师可在实际课堂教学中巧妙设置一些具有一定操作性的问题串，如此既有助于激发学生的创新及探究思维，又能切实锻炼学生的实际动手能力。

如针对“轴对称与轴对称图形”的教学，教师便可在引导学生研究轴对称与坐标变化的知识内容的同时，让学生通过实际操作来辅助分析，如教师可首先在黑板上画出一个直角坐标系，而后要求学生以此连接点（3，0），（5，1），（0，0）等，看最终将形成一个怎样的图形。如此一来，不仅能让学生的学习过程更具趣味性，且能集中学生的学习注意力，继而逐步深化学生对轴对称、轴对称图形以及坐标等知识的理解。

五、引入探究问题串，培养学生探究能力

若学生对所学内容仅是机械化的记忆，则该记忆必将难以得到长久保持。对此，作为初中数学教师，应务必避免让学生采取机械化的记忆方式，并充分彰显学生在实际学习过程中的主体地位，如此方能有效激发学生的学习积极性与主动性，有效调动起学生的探究欲望，逐步增强学生的探究能力。

例如，在教学《勾股定理的应用》内容时，教师可以根据课文内容设置以下问题：通常直角三角形三条边之间存在怎样的等量关系？国际上的诸多科学家都证实了存在勾股定理一说，你能否用文字形式来进行说明，之后用几何语言来说明，最后用公式来表示？是否所有的直角三角形都适用勾股定理？勾股定理可以通过哪些方法来验证？学生在教师所设置的问题基础上进行探索，这里可以看出教师并没有对勾股定理进行过多的证明和论述，而是通过设置问题，引导学生逐步了解勾股定理，通过感知勾股定理，梳理其特征，再进行理性证实。这样教师通过设计“问题串”，不仅有效激活了学生的探究欲望，同时也为学生的分析与思考过程指明了方向，由此不仅能有效锻炼学生的数学思维，且能促进学生综合能力的有效发展。

总之，在初中数学课程教学过程中，不但需要让学生牢固掌握数学概念，而且还需要学生深入理解数学解题技巧和方法，有效拓展学生的数学思维，有效提升初中数学课程的教学水平，增强初中学生的数学素养。