数理金融学的范式危机与变革

● 高 宏

一、引言

数理金融学是一门运用数学理论和方法研究金融市场数量关系及其变化规律的交叉性学科。金融市场大量的实证研究结果和案例分析表明，数理金融学建立的资产价格数学模型与经验事实不一致，不能正确描述资产价格波动现象并预测其变化趋势，数理金融学价格模型及定价公式在金融领域中的广泛应用是导致多次金融危机的罪魁祸首（Triana，2014）。畅销书《黑天鹅》作者Taleb在《金融时报》上发表专栏文章，将数理金融学斥之为“破坏市场的伪科学”。

本文指出了导致数理金融学陷入严重危机的随机变量假设错误，并采用样本函数范式建立了积分形式的股票价格随机游走时间函数模型，演绎推导出了时间自相关函数和功率谱密度函数，从理论上证明了股票价格的可预测性，发现了隐藏在随机游走中的长期线性趋势。

二、危机现象

（一）价格模型与经验事实不符

早在1900年，数理金融学的奠基人、法国数学家Bachelier在其博士论文《投机理论》中，首先应用概率方法对股票价格随时间的变化规律进行研究，发现股票价格的变化是完全随机的，并用随机变量表示任一时刻的股票价格，建立了股票价格算术布朗运动模型。

1958年，美国海军研究实验室的高能物理学家Osborne发现Bachelier的算数布朗运动模型存在股票价格会变为负数的理论缺陷，将其修改为几何布朗运动模型。

由于Osborne也假设股票价格为随机变量，因此几何布朗运动模型的数学期望为零，无法描述和解释股票价格波动中存在的长期线性趋势。为解决这一问题，Samuelson给几何布朗运动模型增加了线性漂移项，建立了带漂移的几何布朗运动模型。但是，线性漂移项中的漂移率为常数，表明股票价格的短期收益率数学期望不为零，意味着股票市场中存在着确定性的盈利机会，与股票价格变化完全随机的观察现象和数理金融学“股票价格短期收益率均值为零”的实证研究结果不符。

此外，几何布朗运动模型假设股票短期收益率服从正态分布，与实际股票收益率呈现出的尖峰厚尾特征和中期随机跳跃现象不符，为了刻画这种小概率极端变化现象，Merton（2013）又在几何布朗运动模型中增加了泊松跳跃过程，但仍然没有解决增加线性漂移项带来的问题。

（二）定价公式导致金融危机

1973年，Black和Scholes基于Samuelson的几何布朗运动模型，推导出了著名的BS期权定价公式。由于从理论上解决了金融衍生产品的定价问题，BS期权定价公式对各种金融创新工具和金融创新产品的面世起到了重大的推动作用，直接导致了“第二次华尔街数学革命”，使金融市场获得了空前规模的发展。

让人意外的是，BS期权定价公式的广泛应用，给金融市场带来了巨大的灾难。由BS期权定价公式衍生出的计算机股票交易策略，成为直接导致1987、1997和2007年三次重大金融危机的主要原因（Mackenzie，2018），数理金融学因此陷入了严重的困境。一些经济学家多年来一直呼吁，几何布朗运动模型无法正确描述资产价格现象，BS期权定价公式永远不应该使用。

三、危机根源

数理金融学在100多年的发展过程中，始终无法解决资产价格数学模型与事实不符的问题，究其原因，是将金融资产价格与时间之间的数量关系错误地假设为随机变量。

1905年，爱因斯坦使用统计方法建立了布朗运动物理模型。1923年，维纳将爱因斯坦的布朗运动物理模型抽象为一个纯粹的随机过程数学模型，为自然科学、工程技术和社会科学等领域研究随机现象提供了基础数学工具，因此布朗运动数学模型也被称为维纳过程。

随机过程是映射到实数轴上的二元函数，有时间和状态两个自变量。对于固定的时间，随机过程退化为状态变量的函数，称为随机变量；对于固定的状态，随机过程退化为时间变量的函数，通常称为样本函数或样本轨道。

爱因斯坦的布朗运动物理模型描述的是多个悬浮粒子的位移概率分布，维纳将多个悬浮粒子的位移抽象为随机变量，在状态空间建立了布朗运动数学模型。因此，维纳过程是定义在状态空间的布朗运动状态变量模型，不是在时域描述单个布朗粒子运动的样本函数模型。维纳过程为非平稳随机过程，不具备各态历经性，其随机变量的统计平均和样本函数的时间平均在概率意义上不等。若将维纳过程随机变量模型及其正态分布、马尔科夫和鞅特性直接用于样本函数，不仅会发生“张冠李戴”式的数学概念错误，还会产生一系列与事实严重不符的结论。

从随机过程角度看，股票价格随时间演变的过程，就相当于一个布朗粒子的位移随时间变化的过程，可视为随机过程试验中的一次测量结果，可用随机过程的一个样本函数来表示。但是，数理金融学却将其假设为随机变量（Hull，2013），这意味着数理金融学的研究对象发生了根本性的变化，研究对象从单个样本函数变化为样本函数集合，并在状态空间求解时域问题，因此，建立的随机数学模型和推导出的所有结论必然存在根本性的概念错误，无法正确描述资产价格波动现象并预测其变化趋势，这就是数理金融学产生严重危机的范式原因。

四、范式变革

观察股票价格随时间变化的过程，虽然股票价格随时间做无规律的随机性变化，但是对于每一个时间值，都有唯一一个确定的股票价格与它对应，因此，股票价格与时间之间的数量关系为确定性的函数关系，在数学上只能被抽象为随机过程样本函数，而非随机过程随机变量。

要建立能够正确描述股票价格随时间演变的数学模型，数理金融学必须要摒弃基于随机变量假设的错误范式，全面转换到基于样本函数假设和函数分析方法的正确范式。

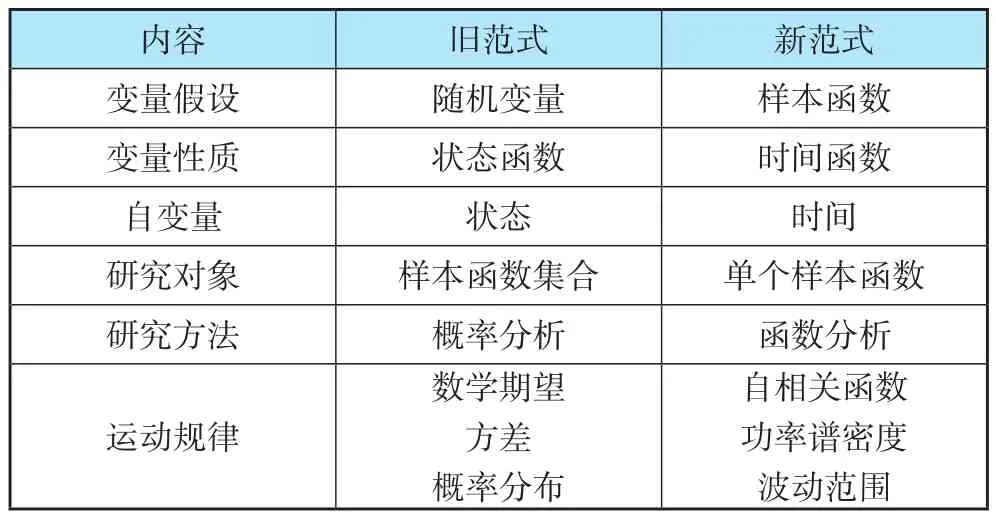
表1 旧范式与新范式对比

从表1的对比可以看出，新范式与旧范式之间没有公约数，只有随机变量和样本函数、状态和时间、集合和元素等质的差别。

五、基本理论

本文使用公理化方法，从基本概念和不加证明的基本定律（公理）出发，演绎推理出可描述股票价格波动现象并揭示其运动规律的一系列基本结论（高宏，2018）。

（一）基本概念

定义：若时间函数x（t）的时间均值为零，时间自相关函数满足

式中为时间间隔，N0为正实常数，δ（t）为单位冲击函数，则称x（t）为白噪声函数，简称白噪声。N0的物理意义代表白噪声信号在单位电阻上产生的平均功率。

式（1）表明，白噪声x（t）仅在时间间隔 =0时才有相关性。因此，白噪声x（t）在时域的波形是一串宽度无限窄、起伏变化极快的随机脉冲（跳跃）。

（二）基本定律

设s（t）为t时刻的股票价格，则股票对数价格（简称股票价格）y（t）=ln s（t）在Δt区间上的一阶差分（对数收益率）为

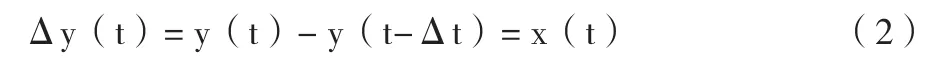
式中x（t）为式（1）定义的白噪声。

式（2）的基本定律表明：股票对数价格的一阶差分为零均值不相关白噪声函数，这是众多学者通过对股票价格波动现象长期观察和实证研究得到的规律性认识。

（三）价格模型

由式（2），有

显然，式（3）为随机游走过程样本函数模型。由于式（1）没有对x（t）的概率分布做任何假设，因此式（3）可以同时描述股票价格的短期随机游走和中期随机跳跃现象。

若假设x（t）服从正态分布，则式（3）就是布朗运动或维纳过程样本函数模型。

将式（2）的差分方程看作离散化微分方程，设y（0）=0，可得积分形式的随机游走模型：

式（4）的模型参数（积分上限）会随时间变化，因此股票价格数学模型为非线性时变模型。

（四）时间自相关函数

股票价格y（t）的时间自相关函数为

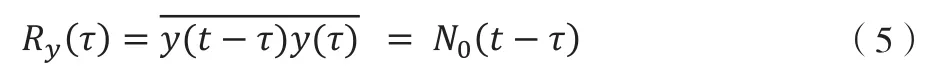
式中，τ为时间间隔。Ry（τ）在很宽的范围内具有非零值，表明股票价格具有可预测性。

（五）功率谱密度函数

股票价格y（t）的平均功率有限，自相关函数Ry（τ）绝对可积，因此根据维纳-辛钦定理，股票价格y（t）的功率谱密度函数Sy（ω）是其时间自相关函数Ry（τ）的傅立叶变换，有

式中，Sinc（ωt）为辛格函数，是正弦函数Sin（ωt）与单调递减函数1/ ωt的乘积。表明股票价格y（t）中的谐波分量波动幅度与频率ω成反比，y（t）为能量集中在低频段的红噪声。

Sy（0）=N0t2，证明y（t）中存在一条与时间t成正比的线性趋势线，y（t）围绕线性趋势线上下波动。

六、结论

本文指出了导致数理金融学陷入严重危机的随机变量假设错误，并根据金融资产价格与时间一一对应的实际现象，将资产价格随时间演变的过程抽象为随机过程样本函数，采用公理化方法建立了积分形式的随机游走时间函数模型，可同时描述股票价格的短期随机游走、中期随机跳跃和长期线性漂移现象，演绎推导出了可揭示金融资产价格运动规律的时间自相关函数和功率谱密度函数，从理论上证明了股票价格的可预测性，发现了隐藏在随机游走过程中的长期线性趋势。可为证券投资活动的量化分析、价格预测、资产定价、最优配置及风险管理提供有效可靠的数学模型和工具。