基于有限元法的贮液瓶跌落响应特性提取方法
李世文,田 雷,田 昱,许曼佳,张 震
(西安机电信息技术研究所,陕西 西安 710065)
0 引言
安全性是引信电源必须具备的技术指标之一,它要求引信电源在贮存、运输、勤务处理过程中不解除保险。常见的安全性试验就是跌落试验,这种方法虽然可靠,但也存在很多不足之处:一是跌落试验历程时间短,只能得到试验结果,很难对试验过程中的特征进行提取,无法观察内部现象;二是试验测试的条件(如碰撞角度等)难以控制,试验重复性差。文献[1]提出了利用MSC. Dytran对引信电源贮液瓶结构进行抗冲击特性及动力响应研究。文献[2]在文献[1]的基础上进一步研究了贮液瓶形状、载荷大小、冲击距离对引信贮液瓶的影响。文献[3]提出了一种考虑扭转力矩的塑料贮液瓶薄弱环节尺寸设计方法。以上文献只研究了贮液瓶在冲击状态下的响应或结构尺寸设计,尚未提取分析贮液瓶在跌落状态下的响应过程。文献[4]提出采用蒙特卡洛方法模拟实现引信安全性跌落检验,将保险弹簧的数据代入惯性元件动力学模型,把虚拟跌落试验结果与弹药事故统计进行对比,该方法是模拟定性分析,跌落过程的微观变化无从谈起。文献[5]针对电子封装的焊接部位进行了有限元模拟,主要研究了跌落的方向对焊点的影响。文献[6]研究了工控设备缓冲包装的跌落数值仿真,从仿真结果中获得跌落加速度曲线和产品的等效应力云图,为本文提供了思路。针对目前无法对引信贮液瓶跌落试验过程响应特性和内部现象进行提取和观察的现状,提出了基于有限元法的引信电源贮液瓶跌落响应特征提取方法。
1 跌落问题描述及有限元法
1.1 问题描述
跌落问题是碰撞问题中的一种,其控制方程和一般碰撞问题没有不同,但在跌落碰撞过程中有应力波传播,局部的塑性变形甚至破坏。在实际的引信跌落试验中,电源装配于跌落试验弹中,不会直接跟障碍物直接碰撞,电池外形可以认为不发生变形。跌落试验对电源要求最严格的结构是装满电解液的贮液瓶,不管是采用重块冲击薄膜激活还是拉断薄弱环节的激活方式,贮液瓶都是引信电源跌落试验中最易出现破坏的薄弱环节。本文研究正是此类最常见的含有薄弱环节的引信电源贮液瓶。由于流体结构相互作用,对此类问题的响应特征提取,采用合理的特征提取方法是重要的前提,任意拉格朗日-欧拉算法可有效分析电解液与塑料瓶之间的复杂关系[7]。
1.2 有限元法
有限元法是一种高效能、常用的数值计算方法。有限元法将连续的求解域离散为一组单元的组合体,用在每个单元内假设的近似函数来分片的表示求解域上待求的未知场函数,近似函数通常由未知场函数,近似函数通常由未知场函数及其导数在单元各节点的数值插值函数来表达,从而使一个连续的无限自由度问题变成离散的有限自由度问题。任意拉格朗日-欧拉算法是常用的一种有限元方法,将计算固体力学中所用的Lagrange方法和计算流体力学所用的Euler方法优点结合了起来,即Arbitrary Lagrange-Euler算法,简称ALE算法。Donea和Belytschko等人分别将ALE算法引入到有限元中,用于解决流体与结构相互作用的问题。Hughes等人建立了ALE描述的运动学理论,并使用有限元法解决了粘性不可压缩流体和自由表面流动问题。自上世纪80年代中期以来,ALE方法已经被广泛用来研究带自由液面的液体晃动问题、固体材料的大变形问题、流固耦合问题等。随着ALE算法的不断完善,一些专业计算软件开始加入ALE功能,ANSYS/LS_DYNA是目前具有较成熟的ALE算法的大型通用有限元程序[8],其内部集成了ALE算法,针对跌落问题有DTM模块可供使用。
1.3 传统跌落判定方法流程
传统的跌落判定方法采用数值计算的方法来判定,以跌落高度来换算跌落过载值,将跌落过载值代入应力计算公式,计算得出应力值与材料屈服应力比较判定,并辅助跌落结果进行对比。流程图如图1所示。
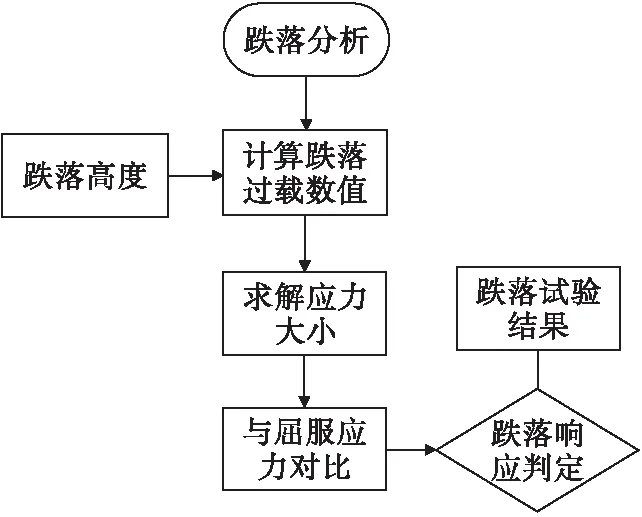
图1 传统判定方法流程图Fig.1 Flowchart of traditional judgment method
2 基于有限元法的跌落响应特性提取方法
由图1可以看出,传统跌落判定方法只能将计算结果与屈服应力比较得出判定结论,无法提取响应特征或观察内部变化。实际跌落结果可以用作辅助比较,但无法量化抗跌落能力余量,无法预估安全跌落高度。
2.1 基于有限元法的跌落特性提取方法流程
基于有限元ALE算法的跌落响应特性提取方法主要依靠ANSYS/LS_DYNA自带的ALE算法来完成,需要进行一些前期工作,包括建模假设、模型参数设置、跌落参数设置,前期工作完成后,进行后处理,观察跌落结果,进行分析。流程图如图2所示。
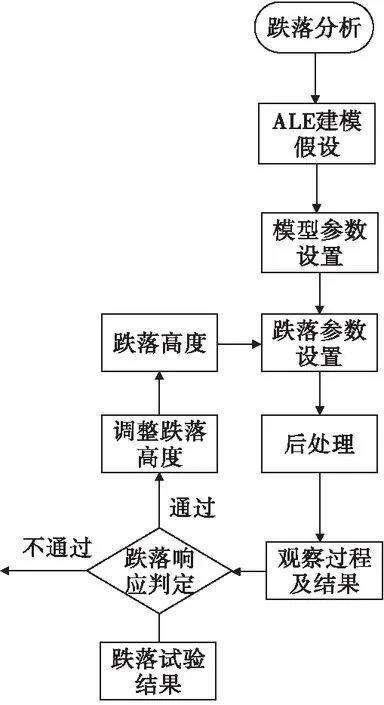
图2 ALE算法的跌落响应特性提取流程图Fig.2 Flowchart of extracting characteristics of drop response based on ALE method
2.2 基于有限元法的跌落响应特性提取
整个响应特征提取过程有建模假设、模型参数设置、跌落参数设置、后处理、内部现象及结果观察等步骤。
跌落测试过程中,引信贮液瓶安装于电源中,电源再装入跌落试验弹中进行跌落。在建模过程中,假设贮液瓶上端与电源、电源与试验弹工装均连接可靠,把电源和跌落试验弹看成是密度均匀的刚体,贮液瓶在试验弹工装中的位置如图3所示。

图3 塑料贮液瓶位置示意图Fig.3 Schematic diagram of theposition of plastic liquid storage bottle
为了简化计算量,同时也加强对引信电源贮液瓶的考核,跌落试验弹、贮液瓶中的加重块都假定为刚体,贮液瓶采用双线性各向同性硬化模型,电解液采用Null材料模型,至此建模的前期假设完成。
模型参数设置工作有定义单元类型、定义材料属性、网格划分、Part定义和接触定义。
定义单元类型及其算法的菜单操作步骤为在ANSYS/LS_DYNA软件操作界面下Main Menu>Preprocessor>Element Type>Add/Edit/Delete命令弹出的Element Types对话框内,单击Add按钮,弹出Library of Element Types对话框。在对话框的下拉列表中选择所需要的单元类型,在Element Type Reference Number区域设置对应的单元类型编号,单击OK或Apply按钮,就完成了对单元的选择操作。
定义材料属性的操作为Main Menu>Preprocessor>Material Props>Material Models,在弹出的Define Material Model Behavior对话框中选择相应的材料模型,输入相关参数,确定材料属性,输入各实体的材料模型参数。
贮液瓶为轴对称结构,为了简化模型建立和仿真过程的工作量,在不影响仿真结构的正确性和真实性的前提下,在此使用贮液瓶模型1/4进行建模。因贮液瓶模型较为复杂,因此先在Inventor中将模型建好,再导入ANSYS中,导入后对贮液瓶模型进行网格划分。划分网格时,需要对网格密度进行控制,选择Main Menu> Preprocessor>Meshing>Mesh Tool命令,使用弹出的网格工具可以控制网格尺寸。选择实体模型完成网格划分得到网格划分后的贮液瓶有限元模型,如图4。

图4 贮液瓶有限元模型Fig.4 Finite element model of liquid storage bottle
选择Main Menu>Preprocessor>LS-DYNA Options>Parts Options命令,在弹出的Parts Data Written for LS-DYNA对话框中选择Create all parts,点击OK完成Part定义操作。
选择Main Menu>Preprocessor>LS-DYNA Options>Contact>Define Contact命令,弹出Contact Parameter Definitions对话框,选择单面接触(Single Surface)和自动(Automatic)完成接触定义。
在ANSYS/LS_DYNA提供的跌落测试模块DTM下快捷地设置跌落测试的基本参数,该DTM模块算法基础就是ALE算法。其具体参数设置包括重力加速度、跌落高度、工装的定位、计算时间、计算输出时间、目标面等材料特性,如图5所示。
程序数据检查无误后,便可进行跌落测试分析
的计算。此时在ANSYS图形界面会显示刚性目标面的位置,被测物体的位置等图示信息,如图6所示。利用ANSYS/LS_DYNA提供的LS_PREPOST后处理器可以直接进行后处理并可提取到跌落响应特征,直观观察到仿真结果。

图6 跌落分析选项设置后的图形显示Fig.6 Flowchart of location information of drop test
3 实例及试验验证分析
3.1 相关参数输入
实例模型选用SOLID164实体单元,无需设置实常数。输入如表1所示的材料属性。

表1 贮液瓶材料属性表
本实例模型采用总体单元来进行尺寸控制,薄弱环节处的网格尺寸将自动变小以增加网格密度。完成单元尺寸控制后,设置划分对象对体(Volume),单元形状为四面体(Tet),以及自由划分(Free),本实例重力加速度为9 810 mm/s2,跌落高度1 500 mm,工装定位垂直向下,计算时间0.06 s,目标面为铸铁板,至此完成各相关参数输入。
3.2 后处理及跌落结果分析
利用ANSYS/LS_DYNA提供的LS_PREPOST后处理器,可以方便地得到1.5 m垂直朝下方向跌落到铸铁板时的应力峰值云图,如图7所示。

图7 1.5 m跌落响应峰值时应力云图Fig.7 Stress cloud of drop test
由图7可知,1.5 m跌落时的最大应力为14.6 MPa,小于贮液瓶的材料屈服应力22 MPa。同时,通过后处理器还方便地看到贮液瓶整个跌落受力响应过程,应力的集中部位从贮液瓶的上端逐渐转移至中部薄弱环节处,如图8所示。同时,处理器也可以给出任一节点的位移、速度、加速度曲线,从而可以观察到各个部位的运动情况。

图8 1.5 m跌落冲击各时段应力云图Fig.8 Various stage stress cloud of drop test
在引信跌落试验中,除了弹底向下,还有弹头朝下、弹底45°朝下、弹头45°朝下、水平跌落等四个方向。通过DTM模块可以方便地模拟出这四个方向的跌落动态过程,如图9所示。1.5 m高度下弹头朝下、弹底45°朝下、弹头45°朝下、水平各个方向跌落结果依次为1.5 MPa,9.5 MPa,9.4 MPa,1.8 MPa,与弹底朝下方向14.6 MPa相比较可以得知,弹底朝下方向是贮液瓶内部应力最大的方向。
同时,我们还可以通过DTM模块考核贮液瓶的最高安全跌落高度。观察不同跌落高度贮液瓶内部应力变化,可以得到贮液瓶的最高跌落高度。图10为不同高度下贮液瓶跌落时的应力云图。1.8 m高度弹底朝下方向跌落最大应力为18.5 MPa,2.0 m弹底朝下方向跌落最大应力为21.7 MPa,非常接近贮液瓶材料本身屈服应力22 MPa,最高安全跌落高度应小于2.0 m。
3.3 跌落试验验证
按照ALE算法所提到的各类参数,装配了一定数量的引信电源进行了各类高度跌落试验,试验结果如表2所示。

图9 贮液瓶不同方向跌落结束的应力云图Fig.9 Various direction stress cloud of drop test

图10 不同高度弹底朝下方向跌落应力云图Fig.10 Various height of bottom direction stress cloud of drop test
试验结果表明,贮液瓶可以满足1.5 m和1.8 m各个方向的跌落考核,2.0 m跌落20%的电源出现不同程度断裂,出现断裂的跌落方向均为弹底朝下。可以看出,除2.0 m高度弹底朝下方向外,其他跌落实际结果与仿真结果完全一致,说明2.0 m高度本身是该贮液瓶安全跌落高度的临界值。2/75的贮液瓶在2.0 m高度跌落后出现不同程度断裂,其误差有可能是贮液瓶机械加工残留应力差异造成。73/75的贮液瓶在安全跌落高度判定结果与实例分析结果一致,安全跌落高度判定准确率达97%。
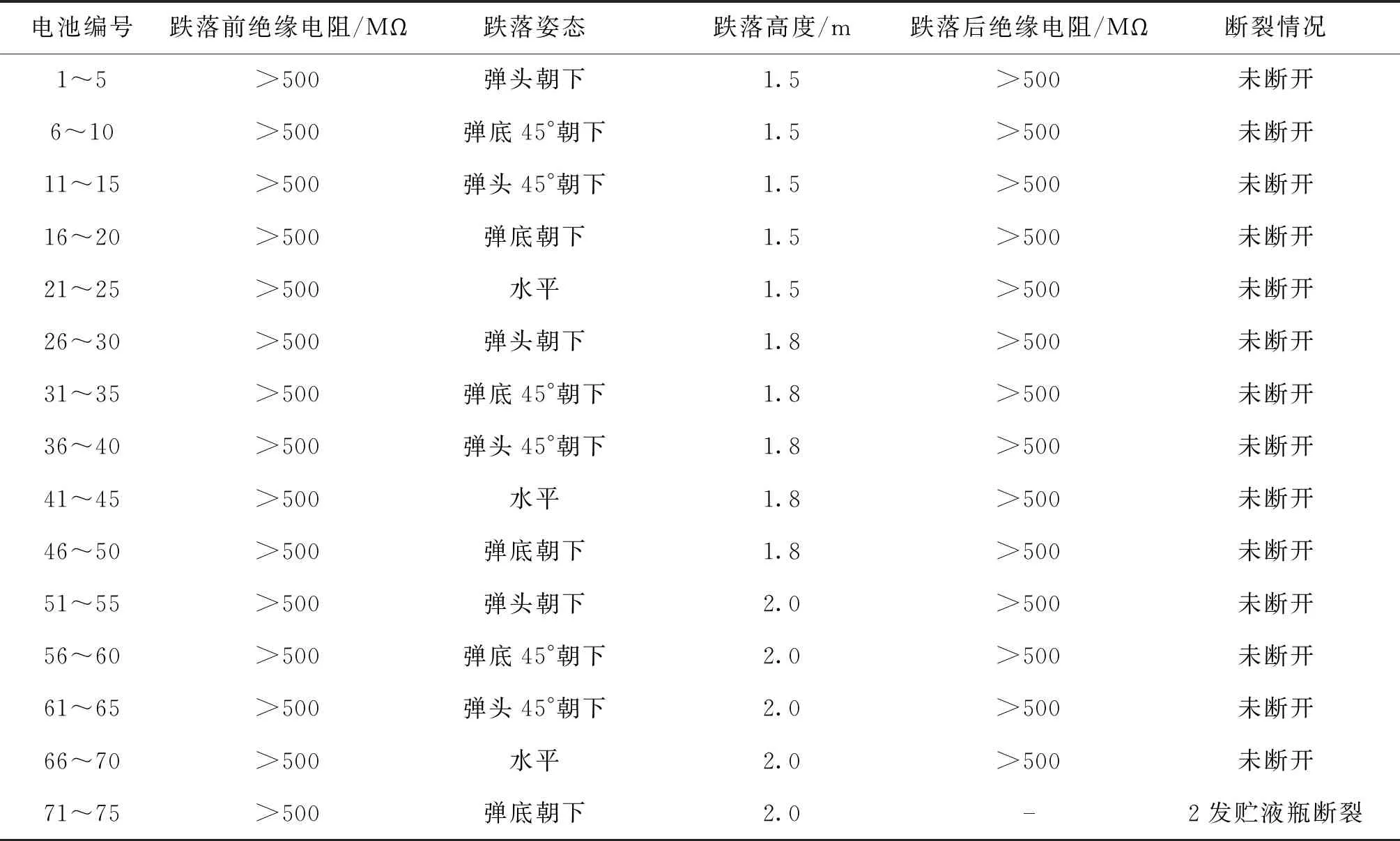
表2 跌落试验结果
4 结论
本文提出了基于有限元法的引信电源贮液瓶跌落响应特征提取方法。该方法利用有限元法中的任意拉格朗日-欧拉算法结合ANSYS/LS_DYNA软件对跌落响应过程进行特征提取,可以清晰地提取贮液瓶整个跌落过程中的应力变化等内部微观变化及特性。实例验证及跌落试验结果表明,该方法可以提取贮液瓶跌落过程响应特征,清晰地观察整个贮液瓶跌落过程中应力变化等微观变化,安全跌落高度判定准确率达97%。后续研究中,可针对贮液瓶发射过程中的响应特征提取等问题进行研究。

