多普勒信号的小波域维纳滤波方法

祁 斐,宁 波,霍鹏飞

(1.西安机电信息技术研究所,陕西 西安 7100652.陆军装备部驻西安地区第四军代室，陕西 西安 710043)

0 引言

为了能够从含噪多普勒信号中准确提取出目标信号,学者们提出了各种去噪方法。经典的时频频法即短时傅里叶变换(STFT),将回波信号分解成若干个窄带子信号,通过频谱变化实现信号检测。由于STFT存在窗函数宽度选择的问题：窗太窄,窗内的信号太短,会导致频率分辨率差；窗太宽,时间分辨率低，其抗噪能力仍有限,因此提出了信号小波域分析方法。该方法利用可变时基,通过尺度参数和平移参数,解决时域窗口的大小和位置问题,从而可以有针对性的对信号的局部区域进行分析。在STFT的基础上结合经验模态分解(EMD)算法,实现对多普勒信号的分离和多普勒信号瞬时频率的估计也是一种有效的时频分析方法[1]。结合经验模态分解和希尔伯特变换将信号高低频分离开再对信号进行处理,得到模态分解信号的瞬时特征进行构造,这种方法对信号的宽带噪声抑制明显[2]。文献[3]在探地雷达的噪声处理上，使用了一维HHT方法，提高了探地雷达信号的解析精度。文献[4]提出了一种基于小波分解的自适应阈值和双边滤波的去噪方法，克服了统一阈值的不足，增强了算法处理的自适应性。这些方法都利用有效信号和噪声在频域内分布特征差异提取有效特征识别信号。

本文针对传统小波变换法阈值去噪方法对低频噪声的抑制不理想的缺点,提出了一种小波分解阈值法和维纳滤波联合的多普勒信号提取方法。

1 多普勒信号时频特征分析

多频谱引信探测系统的回波信号解调后的多普勒信号如图1所示。多普勒信号采用两路回波进行分析来提高系统可靠性。从时域上可见,幅值与目标距离相关；从频域上可见,探测识别信号具有一定的带宽，该带宽为多普勒信号带宽。在不同的距离上,回波信号的幅度不相同,因此可以利用小波变换通过对不同距离上的信号频率特征进行提取,联合幅度特性和速度信息,以检测目标距离,识别多普勒信号并在合适时机可靠判决。

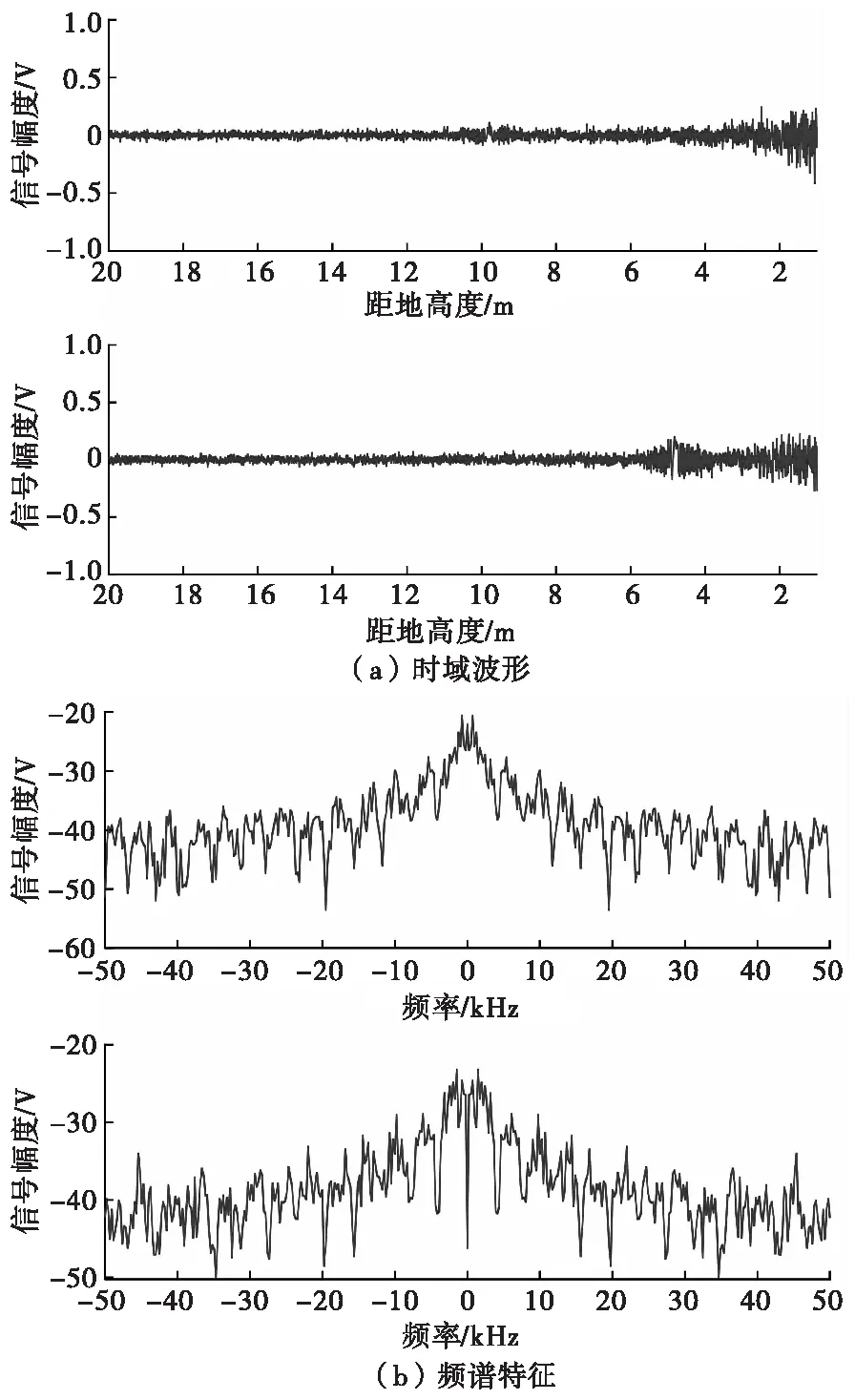
图 1 回波信号解调后时域波形和频谱特性Fig.1 Waveform and spectrum characteristics of demodulated signal

2 小波域去噪方法

小波变换信号分析采用改变时间-频率窗口形状的分析方法,解决了STFT时频分析的时间分辨率和频率分辨率的矛盾,在时间域和频率域都有比较好的局部化性质。对信号低频部分,小波分析采用比较宽的时间窗,得到较高的频率分辨率；在信号的高频部分,采用窄时窗,得到低的频率分辨率。这种小波变换的自适应特性,可以在分析频率变化比较大的平稳信号中有广泛应用[5-6]。

平方可积函数f(t)∈L2(R)的连续小波变换定义如下[7]:

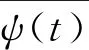
将尺度因子a和位移因子b进行如下离散采样:

则离散小波变换定义为:

Cm,n为离散小波系数。其中，

可由离散小波系数,恢复原始信号f(t)[8]:

小波变换尺度因子a的大小反应了信号频率的大小,当非平稳信号频率随时间变化时,小波变换能够将信号在不同尺度下进行多分辨率的分解,并将交织在一起的各种不同频率组成的混合信号分解成不同频段的子信号,因而对信号具有按频带处理的能力。

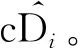
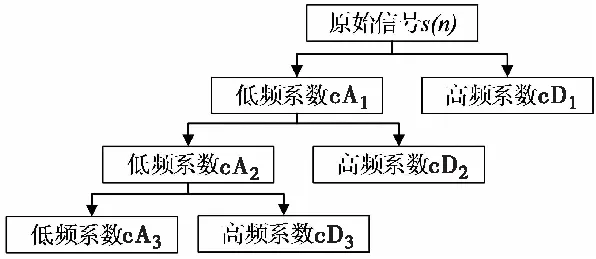
图2 小波分解过程Fig.2 Wavelet decomposition process

阈值法去噪根据白噪声在小波变换域的能量主要集中于幅值较低的小波系数特点, 设计阈值, 使低于该阈值的小波系数变为零, 从而使信号中的噪声得到有效抑制[8]。常用的阈值方法有硬阈值法和软阈值法两种。与硬阈值函数相比,软阈值函数是以连续函数,处理后的小波系数连续性较好。因此,采用软阈值函数进行滤波。

软阈值函数[9]:

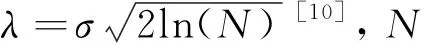
3 低频系数的维纳滤波处理

维纳(Wiener)滤波器是一种经典的线性降噪滤波器,广泛应用于平稳随机信号处理。由图1可看出多普勒回波的原始信号是非平稳信号,因此不能直接进行维纳滤波。而小波变换分解过程,其低频部分相当于对信号进行了去相关,较大程度地降低信号的非平稳随机特性,其低频部分可以近似看作是平稳的。因此,可以将多普勒回波经过小波变换后,对低频部分进行维纳滤波处理。信号处理过程如图3。

对比一组仿真模拟得到的原始多普勒信号与处理后的信号,取原始信号信噪比为0 dB,其处理后输出时域波形如图4所示。

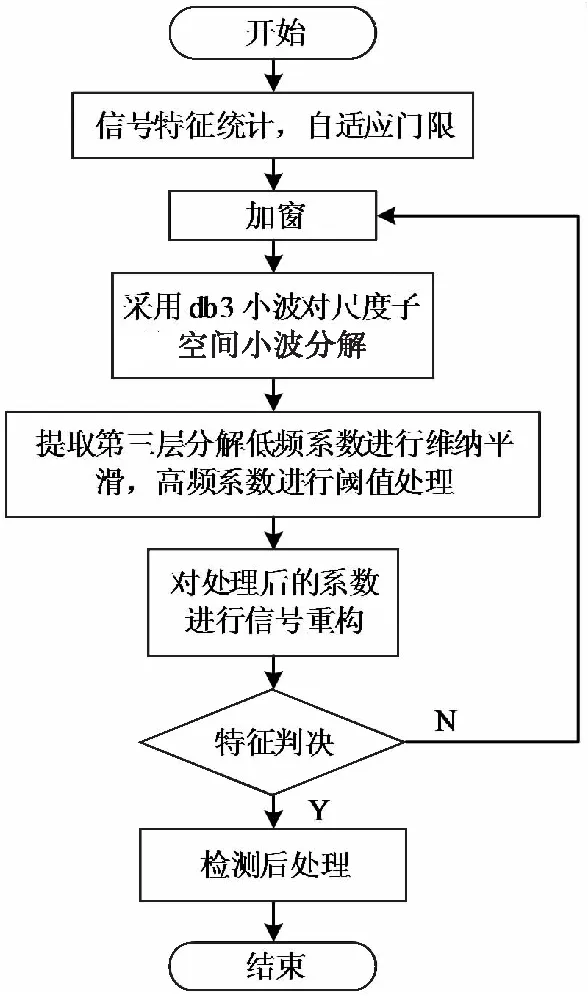
图3 信号处理流程Fig.3 The process of signal processing

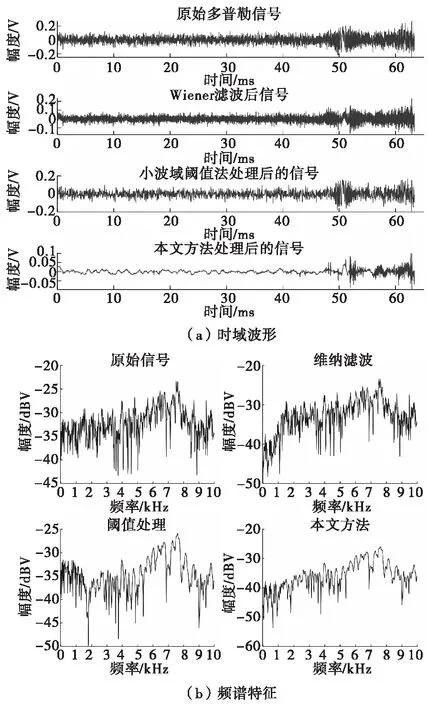
图4 不同方法处理后信号时域波形和目标区域频谱Fig.4 Signal waveforms and target area spectra processed by different methods

从处理后的信号可以看出,在时域上信号波形相对于原始信号有明显改善,在频域上特征多普勒频率的功率损失量也较小。小波阈值处理联合维纳滤波相对于单一小波阈值法去噪或维纳滤波,处理效果明显增强。利用其他几组多普勒信号,在混入不同强度噪声情况下,计算滤波前的信噪比和滤波后的信噪比,本方法的滤波前后信噪比对比结果如表1。

表1 几种不同方法的性能对比

可见,本文方法的噪声抑制性能对比单一维纳滤波和阈值去噪方法,信噪比指标提高明显。为评估此方法对目标检测性能的影响,对STFT方法、小波阈值法和本文方法的检测性能进行了仿真对比。仿真信噪比取-25～20 dB,对原始信号叠加瑞利分布噪声,采用蒙特卡洛方法运行1 000次仿真,对检测结果进行统计,结果如图5、图6、图7所示。

图5 不同处理方法下的检测率Fig.5 Comparison of detection percentage

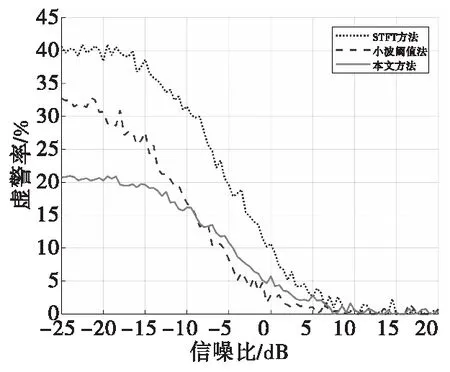
图6 不同处理方法下的虚警率Fig.6 Comparison of false alarm rate

由上图检测率曲线可以看出,在信噪比≤8 dB时,小波域处理的方法检测性能要优于STFT方法。在信噪比≤5 dB时,本文改进的小波域处理方法相对单一的小波阈值处理法有更好的检测性能。在信噪比≤-10 dB时,本文方法相对于STFT法和小波阈值法,虚警率明显降低。在信噪比≥-10 dB时,本方法漏警率小于其他两种方法。综上,在信噪比≤-10 dB时,由于传统小波分解阈值法方法对低频噪声的处理能力不足,其检测能力与经过对低频分量进一步处理的本文的方法比较,需要比较高的信噪比才能有更好的检测能力。本文方法在多普勒小信号的处理上,相对STFT方法或者单一的小波分解阈值处理方法,有更好的目标检测性能。在复杂噪声环境下,本文方法可以提升目标探测能力。

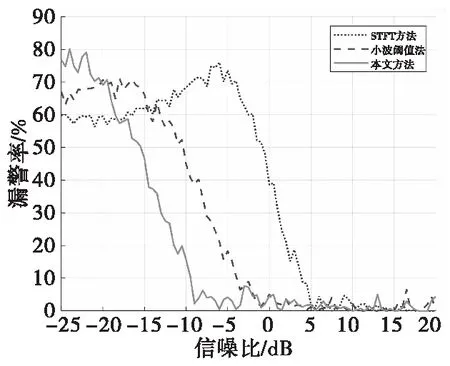
图7 不同处理方法下漏警率Fig.7 Comparison of missing alarm rate

4 结论

本文提出了小波变换阈值处理和维纳滤波联合的多普勒信号去噪方法。该方法在小波阈值法去噪的基础上,对信号的低频小波系数进行维纳平滑处理,然后系数重构得到多普勒信号,仿真验证结果表明,通过小波变换下对小波分解系数进行进一步的维纳滤波,在多普勒回波信号处理过程中得到了比较理想的结果,多普勒信号的提取能力改善,并优于STFT方法和传统的小波域处理方法。尤其在背景噪声比较大的小信噪比情况下,目标检测能力提升显著。