迫击炮弹引信精确制导组件气动外形优化
许立松,闻 泉,王雨时,马国梁,朱远海
(1.南京理工大学机械工程学院,江苏 南京 210094;2.南京理工大学能源与动力工程学院,江苏 南京 210094;3.安徽东风机电科技股份有限公司,安徽 合肥 230000)
0 引言
弹道修正引信是在保留传统引信功能的基础上,增设了感知及辨识弹道环境和弹道修正功能[1],从而使得常规弹丸在装配之后能够获得二维弹道修正能力。
国外对于固定鸭舵式引信制导组件的研究比较成熟,以固定鸭舵式精确制导组件PGK(Precision Guidance Kit)为典型代表的二维弹道修正弹药已经取得良好的效果。该精确制导组件在M934迫击炮弹上的升级应用提供了完善的迫击炮弹制导组件MGK(Mortar Guidance Kit)方案。
固定鸭舵由带有固定斜置角的一对差动舵和一对控制舵组成,通过适当调整鸭舵滚转角来产生控制力和力矩对弹体位置进行修正。这种方法在解耦控制上有一定难度,但是体积小、结构简单,是目前大部分二维弹道修正弹所采用的形式[2-11]。
我国在二维弹道修正技术的研究方面起步较晚,但近年来取得了较多成果[10]。文献[3—4]等对于鸭舵式二维弹道修正原理与机构进行了研究分析。文献[5—8]等采用了风洞实验以及Fluent计算仿真技术对固定舵二维弹道修正弹的鸭舵以及弹丸整体气动特性进行了相关分析。文献[9—11]等对于弹道修正弹的制导与控制系统和落点预测等方面进行了研究,并提出了相应的控制模型和预测算法。
目前的研究主要集中于初速较高的高旋弹丸,针对低速条件下的尾翼稳定弹丸的研究还比较少。为了给迫击炮弹二维弹道修正精确制导组件气动设计提供参考,本文将Fluent流体仿真与编制的外弹道解算程序相结合,对固定鸭舵式迫击炮弹精确制导组件进行气动外形优化设计。
1 数值仿真方法与验证
1.1 流体仿真模型的建立
Fluent软件中给出了大量的计算模型。对于本次的气动分析,选择Spalart-Allmaras (S-A) 模型[12]。S-A模型是为气动领域设计的,计算量小,修正后,涡粘系数在近壁面处容易求解,适用于气动分析。
1.1.1网格划分
采用非结构体网格,将计算模型划分为四面体网格[13],网格单元数量为3 917 698。采用Fluent的Make Polyhedra命令将四面体网格转化为多面体网格以提高仿真结果准确性,转化之后的网格模型如图1所示。
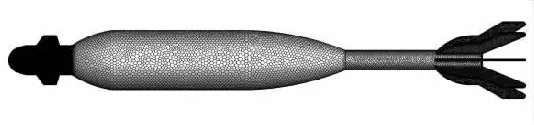
图1 仿真模型多面体网格Fig.1 Polyhedral mesh of simulation model
1.1.2边界条件
求解过程中流场外壁面使用压力远场(Pressure-Far-Field)边界,弹体表面采用wall壁面边界。
1.2 外弹道解算
1.2.1二维弹道修正迫击炮弹简化运动方程
首先建立坐标系,本次分析所建立的地面坐标系O0X0Y0Z0(E)、基准坐标系ONXNYNZN(N)、速度坐标系(弹道坐标系)OXYZ(V)、速度坐标系变换而来的第二弹轴坐标系Oξ2η2ζ2(A2)及相应转换方程同外弹道学描述相同[14],不再赘述。
由于鸭舵修正机构的加入,需要添加鸭舵坐标系OXdYdZd(D)。鸭舵坐标系原点位于质心,由第二弹轴坐标系绕Oξ2轴旋转γ角变换而来,如图3所示。
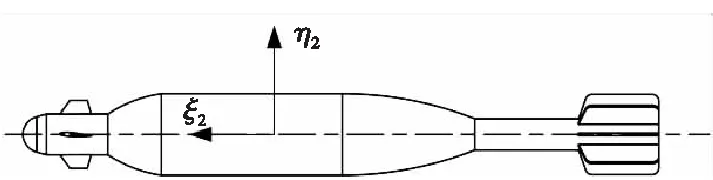
图2 第二弹轴坐标系定义Fig.2 Definition of the second projectile axis coordinate system
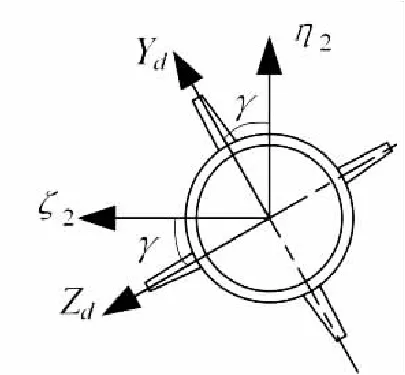
图3 鸭舵坐标系定义Fig.3 Definition of duck rudder coordinate system
迫击炮弹转速较低,故将极阻尼力矩以及马格努斯力和力矩的作用忽略。
对于赤道阻尼力矩Mzz,其表达式为:
(1)
在尾翼弹中,赤道俯仰阻尼力矩主要来源为尾翼,依据弹丸空气动力学[15]中对于尾翼弹赤道阻尼力矩的描述,其产生来源为弹丸自转造成的附加迎角δw,继而产生了附加升力Rzz,从而产生了赤道阻尼力矩。因而可通过Fluent仿真所得的尾翼随攻角的升力系数变化规律求得赤道阻力力矩系数:
(2)
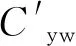
将整个弹道过程分为两个部分,第一部分为无修正过程,第二部分为二维修正过程。无修正过程的弹丸攻角变化对于弹道影响不大,而修正过程中弹丸期望攻角主要由鸭舵控制产生,因而忽略其他扰动,认为修正时弹丸攻角完全由鸭舵控制力矩产生,从而弹丸攻角平面始终在鸭舵坐标系的XdYd平面内。忽略舵滚转角变化的动态过程的影响,认为舵滚转角瞬间到达。舵在γ滚转角下的二维弹道修正弹丸运动方程[11]为:
(3)
式(3)中,Rx,Ry为弹丸阻力以及升力,已经包含舵的表征,ωδ为绕质心在攻角平面的角速度,Jz为赤道转动惯量(0.628 kg/mm2),Cx(δ)为阻力系数,Cy(δ)为升力系数,Mbz为弹丸俯仰力矩,Mzz为赤道阻尼力矩,S为弹丸参考面积,取为最大截面积,l为弹丸参考长度(取为弹长,改进后弹丸长度1.05 m),ρ(y)为与高度相关的空气密度,δ为弹丸攻角,δ1和δ2是弹轴坐标系由速度坐标系旋转而来的角度变换量,θ和ψ为速度坐标系由基准坐标系旋转而来的角度变换量。
采用四阶龙格-库塔法编写外弹道解算程序,解算外弹道诸元。
1.3 仿真计算方法验证
为了验证计算方法的可信性,将原迫击炮弹划分为四面体网格,单元数量2 075 526。采用Fluent的Make Polyhedra命令将四面体网格转化为多面体网格,网格模型如图4所示。

图4 原迫击炮弹仿真模型多面体网格Fig.4 Polyhedral mesh of the original mortar shell simulation model
将导入Fluent仿真得到原迫击炮弹气动参数代入计算程序解算弹道诸元,部分仿真计算结果与已有迫击炮弹射表数据对比以及误差如表 1、表 2所列。从表 2可以看到,射程和落速的最大误差为1.16%,在可接受的精度范围之内。
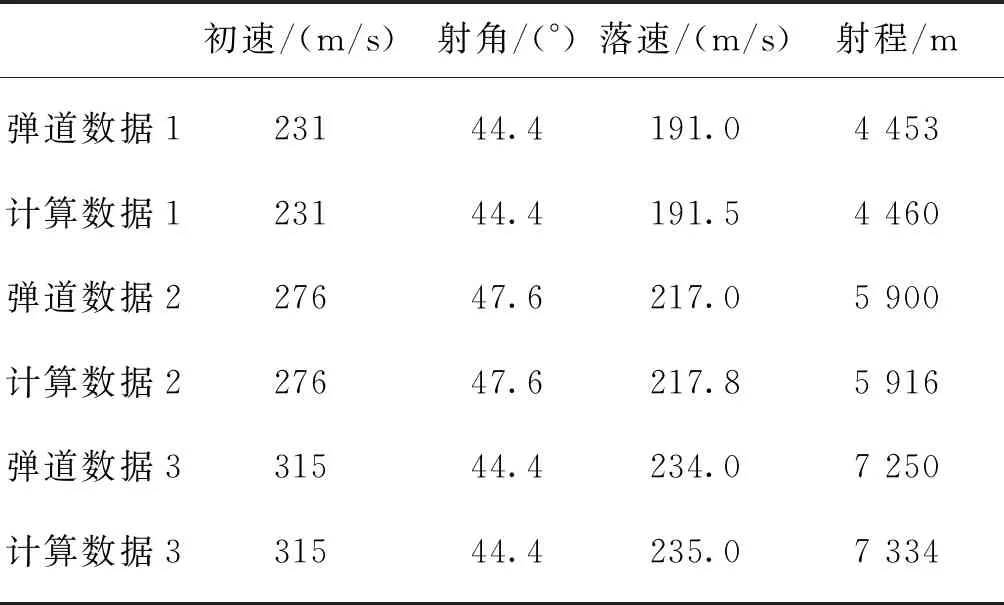
表1 计算仿真与弹道数据对比
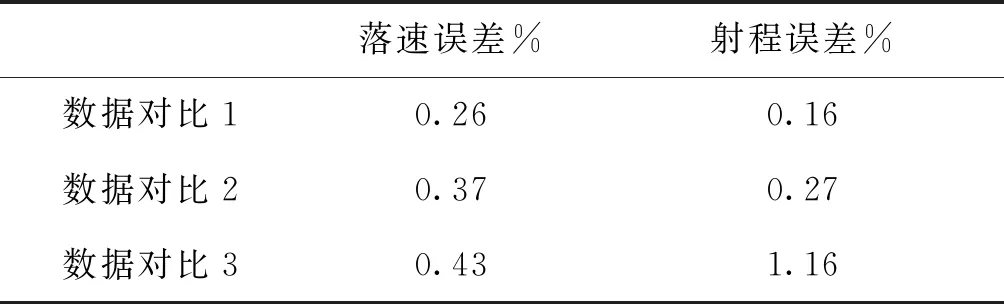
表2 计算仿真与弹道数据误差
2 仿真优化设计
2.1 原迫击炮弹弹道参数仿真计算
通过Fluent仿真确定了原迫击炮弹气动参数,将不同装药号所得初速代入外弹道解算程序,可得原迫击炮弹在45°射角、不同初速下的弹道参数,分别如图5和图6所示。目的是为了得到弹丸在飞行过程的最低速度以及对应修正段的速度分布计算参考值。
根据图6取最小速度为105 m/s,此时气动力最小,修正能力最弱。修正段速度分布是Fluent仿真弹丸气动参数的初值参考。根据图6,仿真时可取速度分布点0.3Ma,0.4Ma,0.5Ma,0.6Ma,0.7Ma。
根据1.2.1节中对于弹丸攻角假设,δ1=δ,在速度坐标系下表现为正,则取验证的攻角值分别取0°,1°,2°,3°,5°。
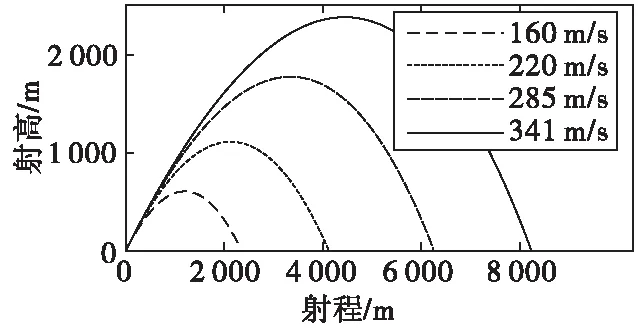
图5 原无控迫击炮弹位置曲线Fig.5 Position curve of original uncontrolled mortar shells

图6 原无控迫击炮弹速度曲线Fig.6 Velocity curve of the original uncontrolled mortar shell
2.2 鸭舵参数设计
常用的翼型系列如图7所示。其在同一雷诺数下的升力系数、阻力系数、升阻比分别如图8—图10所示。
根据技术指标中的设计要求,控制舵在修正时间t(25 s)内滚转角为90°时,即鸭舵升力方向与横向修正方向相同时可达到最大横向修正距离。由于设计之初无法获得弹丸具体气动参数,因而暂将鸭舵升力作为修正力,并将原给定最大横向修正距离Lc(100 m)作为评估标准。在修正能力最弱,即弹丸速度为105 m/s时,根据式(4),可初步估算出单个舵面面积S为723 mm2。结合翼型弦长、展弦比以及弹丸口径,暂初步设计满足舵面面积要求的鸭舵如图11所示,其可行性需要进一步通过仿真进行验证。
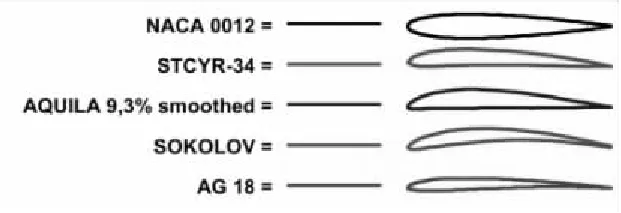
图7 典型翼型Fig.7 Typical airfoil
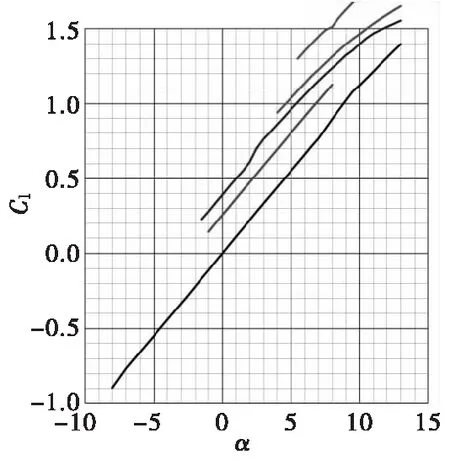
图8 翼型升力系数Fig.8 Airfoil lift coefficient
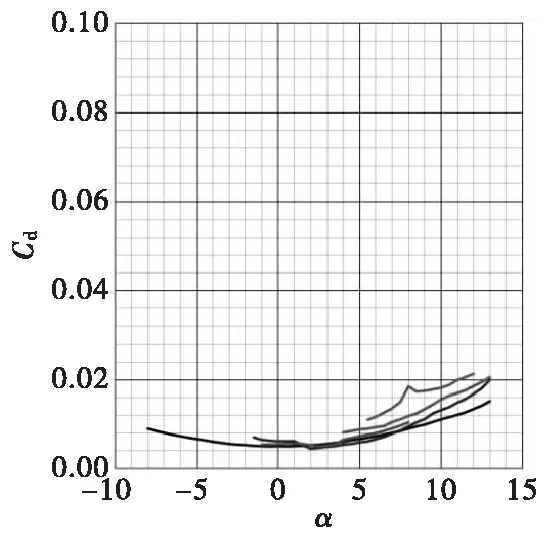
图9 翼型阻力系数Fig.9 Airfoil drag coefficient
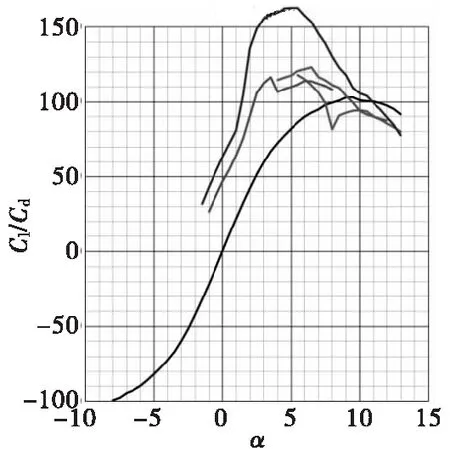
图10 翼型升阻比Fig.10 Lift-drag ratio of airfoil
(4)
式(4)中,FL为鸭舵产生的升力(单位N),即控制力Fd;S为舵面积(单位mm2);ρ为空气密度(kg/m3),C为翼型在相应攻角下的升力系数。
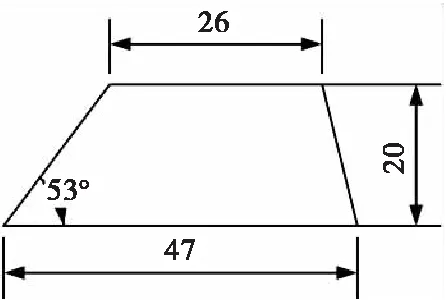
图11 舵面参数Fig.11 Rudder parameters
2.3 鸭舵位置确定
鸭舵会增加弹丸不稳定性,初定三组不同位置鸭舵如图12所示。导入Fluent计算其在1°攻角下的压心位置是否满足条件。
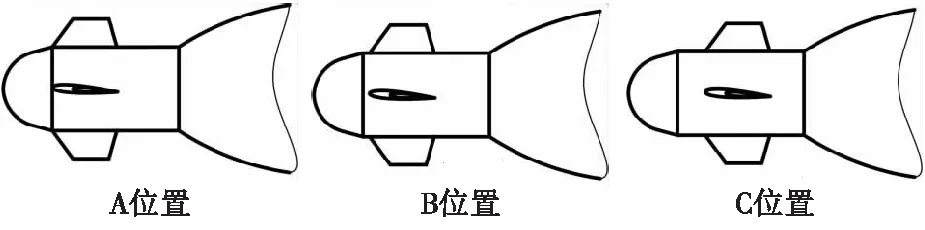
图12 不同舵位置对比图Fig.12 Comparison of different rudder positions
攻角为1°时压心随舵位置变化(距头部顶点)如图13所示。可以看到随着距离的增加,距离对于压心的影响逐渐减少,此时压心位置仍然不满足条件,若继续后移鸭舵,会因距离弹体过近导致气流分离,舵效减小。同时鸭舵的安装还需要与轴承以及电磁控制结构相配合,距离弹体过近可能干扰引信内部电子舱以及传爆序列的布局。
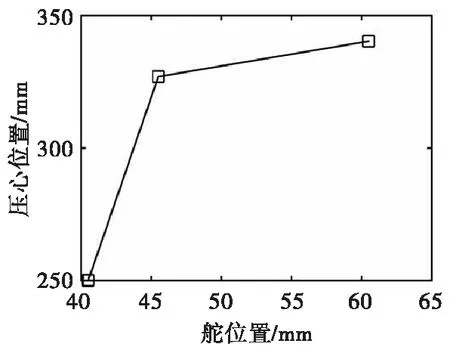
图13 压心随舵位置变化Fig.13 Pressure center changes with rudder position
由上述分析确定鸭舵固定位置为图12中C所示,距离弹丸头部原点距离为X正向60.5 mm。
2.4 尾翼参数确定
为了保证弹丸稳定性,需要对图14所示的原尾翼形式进行改进,参考美军MGK的外形,改进后的尾翼形式如图15所示。将模型导入Fluent进行仿真并进行如图16所示受力分析[16]。
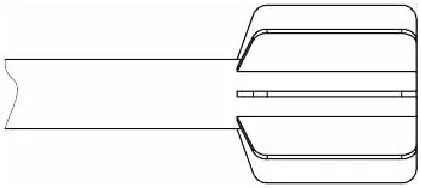
图14 改进前尾翼形式Fig.14 Tail before improved
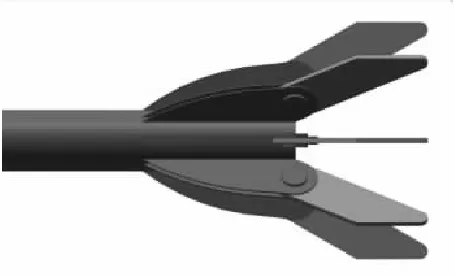
图15 改进后尾翼形式Fig.15 Modified tail
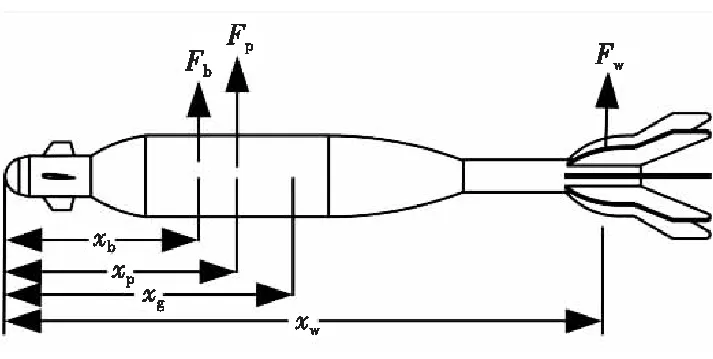
图16 弹丸压心计算分析Fig.16 Calculation and analysis of projectile pressure center
此时将弹体受力分为尾翼受力Fw以及除尾翼以外的弹体受力Fb,它们的作用为分别为xw和xb,对头部原点产生的力矩为Mw和Mb。压力位置为xp,整个弹体所受空气动力为Fp,产生力矩为Mp,弹体质心位置为xg。
求解压心位置,有公式:
(5)
式(5)中尾翼受力可解算为:
(6)
式(6)中,Sw为此时的当量面积,只和单个尾翼的面积Sw0、形状和弹丸攻角有关。
改进时采用折叠尾翼,其基本构造不变,等效于于增加了单片尾翼面积,并且仿真计算时其余条件相同,因而将尾翼受力简化为与系数K和Sw相关的函数:
Fw=KSw
(7)
于是将公式改写为:
(8)
通过式(8)可求取目标静稳定度下,即xp=501 mm时所需尾翼面积Swl为4 505.63 m2。
根据上述结果,对尾翼重新设计后面积为4 567 mm2。导入Fluent仿真得xp为506 mm,与计算值误差为1 %。
由2.1—2.4节的优化设计可得弹丸最终整体结构如图17所示。
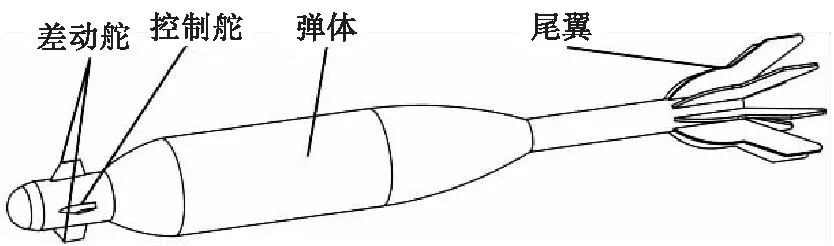
图17 优化后弹丸整体结构Fig.17 Overall structure of optimized projectile
3 仿真结果分析
为了验证设计方案的正确性,将弹丸模型导入Fluent进行仿真分析,可得不同工况下的相关气动参数。
3.1 稳定储备量
不同马赫数下压心位置随攻角变化如图18所示。从图18可以看到弹丸压心位置(距头部顶点)位于506 mm至586.55 mm之间,计算可得稳定储备量保持在7 %到14.7 %之间,满足5 %到15 %的设计要求。
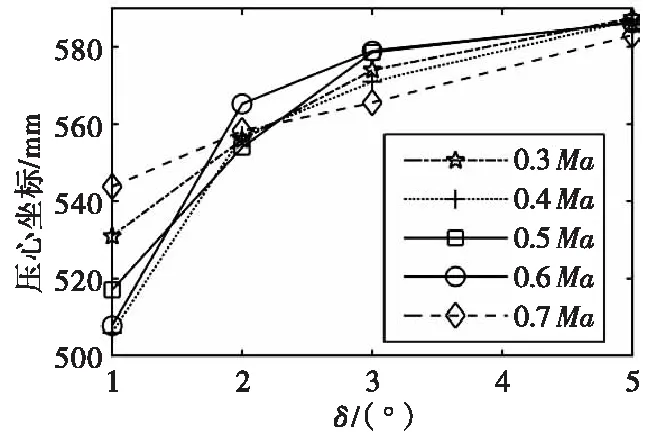
图18 不同马赫数下压心位置随攻角变化Fig.18 Pressure center position changes with attack angle at different Mach
3.2 阻力系数分析
阻力系数不仅仅与攻角相关,同时还受弹丸速度影响,随弹丸速度和攻角变化的阻力系数如图19所示。此时阻力系数可拟合为:
Cx=0.113M2+0.001 664δ2+0.001 718δM-
0.001 403δ-0.128 1M+0.217
(9)
式(9)中,M为马赫数。
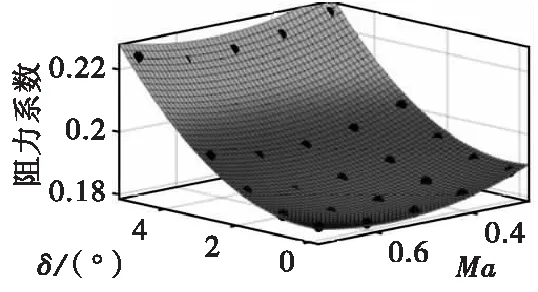
图19 阻力系数随二维变量分布Fig.19 Drag coefficient distribution with two-dimensional variables
3.3 升力系数分析
弹丸在不同马赫数下升力系数随攻角变化曲线如图20所示。由图20可以看出,升力系数随攻角呈线性变化,拟合表达式为:
Cy=Cy0+Cy′δ=0.002 690 3+0.073 977δ
(10)
3.4 全弹俯仰力矩变化分析
不同马赫数下全弹俯仰力矩系数随攻角变化如图21所示。由于鸭舵斜置角的存在,即使忽略其他扰动,在弹丸攻角为0°时,弹丸仍然受翻转力矩作用,从而产生攻角。由图22可知全弹俯仰力矩系数为零时攻角为0.485°,此角度也应为弹丸攻角最终稳定角。
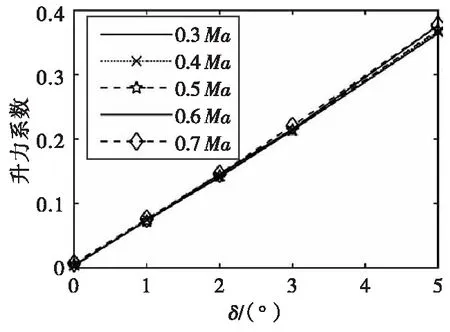
图20 不同马赫数下升力系数随攻角变化Fig.20 Lift coefficient changes with attack angle at different Mach
可以看到其在亚音速区间表现为线性分布,符合理论推导的结果,将其拟合为:
(11)
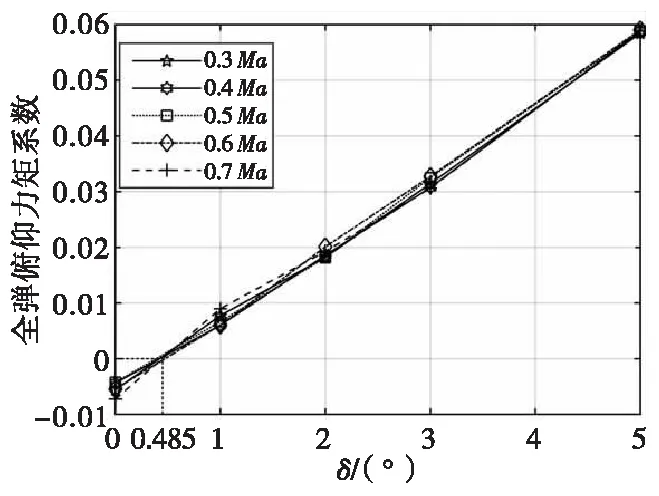
图21 不同马赫数全弹俯仰力矩系数随攻角变化Fig.21 Pitching moment coefficient of projectile changes with attack angle at different Mach
3.5 鸭舵俯仰力矩变化分析
不同马赫数鸭舵俯仰力矩系数随攻角变化如图22所示。从图22可以看到鸭舵造成的俯仰力矩变化较为平缓,接近线性变化,更利于控制功能的实现。
3.6 尾翼俯仰力矩系数分析
尾翼升力系数可通过式(12)由仿真所得俯仰力矩计算得出。
(12)
式(12)中,ρ为空气密度,在Fluent仿真条件中取温度300 K,标准大气压下密度,1.17 kg/m3;(xpw-xg)为0.95 m;Sw为尾翼参考面积,这里取为一对尾翼面积的2倍,0.018 m2。
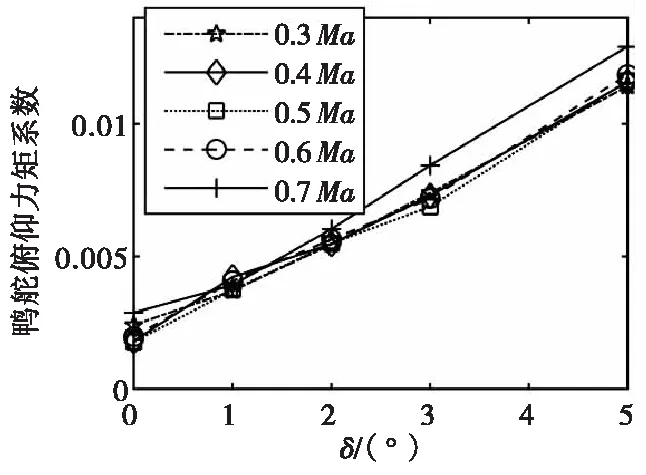
图22 不同马赫数鸭舵俯仰力矩系数随攻角变化Fig.22 Pitching moment coefficients of duck rudder changes with attack angle at different Mach
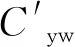
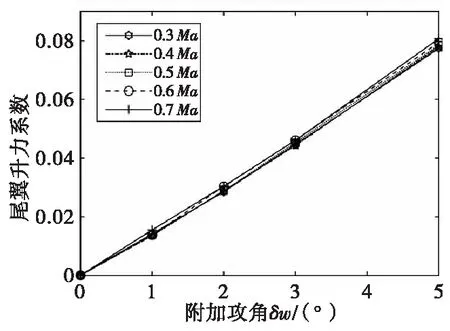
图23 尾翼升力系数随附加攻角变化Fig.23 Lift coefficient of the tail changes with the additional attack angle
3.7 流场分析
0.5Ma时鸭舵处流线随攻角变化和0.5Ma时尾翼处流线随攻角变化分别如图24和图25所示。可以看到底部有明显涡流区,其低压分布是造成弹丸底阻的主要原因。
随着攻角的加大,舵面后方涡流范围加大并且开始后移,气流有分离趋势。尾翼处流线表明随着攻角的变化涡流区产生了偏移,这也会造成弹丸不稳定。
整体来看,弹丸以及鸭舵周围流场均较为稳定,舵效较好。

图24 0.5 Ma时不同攻角下鸭舵处流线Fig.24 Streamline at duck rudder at 0.5 Ma at different angles of attack

图25 0.5 Ma时不同攻角下尾翼处流线Fig.25 Streamline at tail at 0.5 Ma at different angles of attack
4 修正能力仿真验证
极限情况下将舵滚转角γ设为90°代入式(3)即可验证最大横向修正量。
图26给出了发射角为45°、发射初速341 m/s时原迫击炮弹、二维弹道修正迫击炮弹以及二维弹道修正迫击炮弹不进行修正的弹道曲线。可以看到弹丸的修正距离达到了112.61 m,考虑实际过程中的损失,安全裕量完全满足最大射程下横向修正50 m的要求。同时由于舵导致的弹丸阻力系数的增加,二维弹道修正迫击炮弹的射程相比于原迫击炮弹有所降低,射程损失为6.8%。
本文研究的制式弹最大攻角为5°,控制开始前受控弹攻角在正负最大值间随机变化,但攻角最大时最易失稳,从图27横向修正时攻角随时间变化可以看出,控制舵开始作用后,弹丸攻角产生振荡,最终稳定在0.485°。
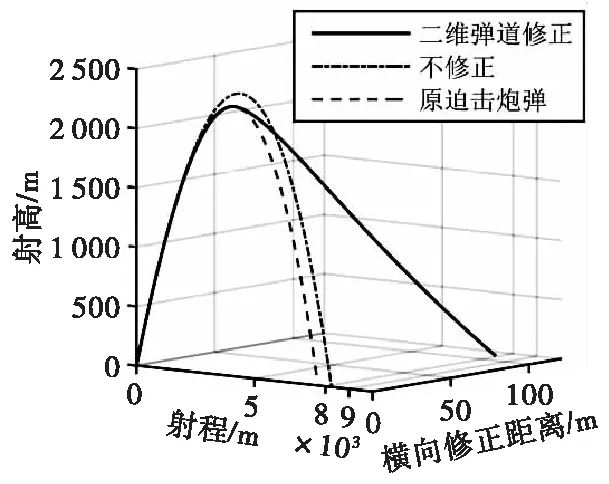
图26 二维弹道修正迫击炮弹修正能力验证Fig.26 Verification of correction capability of two-dimensional ballistic correction mortar shell
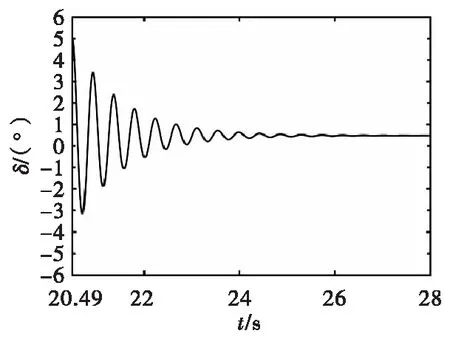
图27 横向修正时攻角随时间变化Fig.27 Attack angle changes with time during lateral correction
5 结论
本文通过将Fluent流体仿真以及外弹道解算相结合,对二维弹道修正精确制导组件的气动外形进行了优化设计。通过仿真计算,得到了鸭舵位置变化、翼型形状对于弹丸气动特性的影响,通过仿真计算方法得到了不同马赫数和攻角下弹丸的升力系数、阻力系数、俯仰力矩系数以及鸭舵和尾翼各项参数。
所得结论如下:
1) 对于固定鸭舵的二维弹道修正引信,鸭舵的添加后明显增大了弹丸阻力系数,并且鸭舵的位置越靠近弹体顶部,越不利于弹丸的稳定。
2) 对于所配用的迫击炮弹,鸭舵截面翼型取低速翼型系列中相对弯度为0,最大弯度为0,相对厚度为12%,单个鸭舵面积取723 mm2、控制舵斜置角为4°、差动舵斜置角为6°、单个尾翼面积为4 567 mm2,在弹丸初速341 m/s,射角45°时的最大横向修正距离可达112.61 m,满足设计要求。

