基于多级决策的云爆弹最佳起爆时机判断方法

张涪森,马 君,张 珂,2

(1.机电动态控制重点实验室,陕西 西安710065；2.复杂系统智能控制与决策国家重点实验室,北京 100081)

0 引言

国内云爆弹药研制从20世纪70年代开始已40多年。对云爆弹而言,由于只有在云爆剂扩散至合适的浓度范围内起爆战斗部才能形成爆轰,产生高温、高压的冲击波,达到摧毁目标的效果。因而,最佳起爆时机研究一直是云爆弹的核心研究内容。

云爆剂起爆的关键是判断云团浓度是否到达爆轰浓度范围。文献[1]通过建立高速摄像机与同步触发器的测试系统,观察云雾的几何尺寸,并运用图像分割处理分析得到浓度变化规律。文献[2]通过对云爆弹建立相关的有限元模型,运用数值模拟与理论计算分析了抛撒方式,壳体材料等因素对浓度的影响。文献[3]简述了延时起爆的作用原理,将二次引信装定精确的延迟时间,达到最佳起爆的目的。建立在实验与理论分析之上的延时起爆方法可靠性高,但存在着缺乏判断能力的问题。文献[4]中提出二次起爆引信对云雾浓度实时检测并判断起爆时机的构想,这一方法可以更好地适应环境,但大型云爆弹燃料抛洒范围巨大,浓度检测装置只能实时测量气雾团中局部浓度,所以要以局部浓度信息对整体气雾团浓度做出估计。当云爆剂由于环境导致浓度分布不均匀时,检测的样本方差相对较大。文献[4]中所运用的算术平均值方法并不能判断云雾整体是否分布均匀,此时存在对最佳起爆时机产生误判的问题。本文针对此问题,提出了基于多级决策的云爆弹最佳起爆时机判断方法。

1 多点浓度检测引信原理

二次型云爆弹为了增加二次起爆的可靠性,均采用多点引信——即多炸点起爆方法。文献[4]中给多点引信配置浓度检测模块,利用激光透射法实时检测云爆剂云团中炸点位置浓度信息。其中某一节点设定为主节点,各节点将检测到的浓度数据上报给主节点,主节点采用算术平均的方法处理浓度数据。该数据均为燃料气体体积占测量总体积的百分比,可以表示为:

(1)

式(1)中，Ci表示第i个浓度检测节点检测到的气体百分比浓度，Vi表示局部燃料体积，Va表示测量总体积。假设多点浓度检测引信系统中有N个浓度检测节点,将t0时刻的浓度信息上报给主节点,主节点做算术平均运算,即有:

(2)

之后将结果与预定门限比较。通常门限取云爆剂所含燃料的爆轰浓度范围。当满足门限要求时,主节点判断云团整体已达到最佳起爆时机,同时向外广播式发送同步起爆信号使各引信作用。

实际云爆弹应用中,由于云爆弹总体指标要求,一枚云爆弹可装载的浓度检测引信数量屈指可数,所以上报的局部浓度信息数量也十分有限。当气雾团内部浓度分布不均匀时,此时采集到的浓度样本可能会出现方差过大的问题,但方差值对算术平均求得的均值并没有影响,所以算术平均值法在浓度还没有分散均匀时,容易误判起爆时机。

2 基于多级决策法判断云爆剂最佳起爆时机

2.1 多级决策算法

多级决策算法又称动态规划算法,是美国数学家贝尔曼(R.Bellman)在上世纪50年代初提出的一种针对动态问题找寻最优决策的算法。他的“最优性原理”及其解法一直是人们解决决策问题的理论依据。只要给出当前阶段的状态参数,就可以进行当前阶段的决策。

多级决策最优原理由第一阶段起,每一级都是针对每一状态选择了由开始至当前之中的最优的,那么到最后阶段做出决策时便形成了整体最优。依据此原理,解题步骤由始点开始,向终点进行。以目标函数累积值最大或最小进行决策,其基本方程为:

(3)

2.2 浓度检测引信起爆时机判断模型

在云爆弹浓度检测引信系统之中,我们定义有n个决策节点。对于每一个n∈{1,2,…,n},第n个决策节点检测到的浓度为xn∈Rm,这里m为正整数。

根据节点1检测得到的浓度x1判断目标函数即云雾爆轰威力的表达式为:

Q(x)=〈a1,x1〉

(4)

式(4)中,Q(x)为线性规划的目标函数；a1为影响目标函数的另一些参数,与检测节点的运动速度v以及炸点位置p有关,根据云爆弹总体设计,在这里假定ai为已知条件。

显然上述情况为最简单的考虑,在实际情况当中,浓度检测节点往往不止一个。根据节点1，节点2，…，节点n检测得到的浓度x1，x2，…，xn判断爆炸威力的表达式为:

Q(x)=〈a1,x1〉⊙〈a2,x2〉⊙…⊙〈an,xn〉

(5)

式(5)中,⊙表示某种运算,当各个检测节点所检测的浓度范围不相互重叠时,该运算可以是加法。判断云爆弹最佳起爆时机可等效为判决云雾爆炸威力最大的过程,即可以表示为:

φ=max{〈a1,x1〉+〈a2,x2〉+…+〈an,xn〉}

(6)

决策节点选择X的值,使得X=(x1,x2,…,xn)满足X={x∈Rn,Bx1≥b}。这里B是n×m的矩阵,b∈R。每一级决策节点依次选择变量{xn∈Rn}的值,使由〈an,xn〉决定的它的目标函数最大。

即当X={x∈Rn,B1x1+B2x2+…+Bnxn≥b}时,X作为φ的最优解。

2.3 算法实现

由以上论述,应用多级决策算法判决云爆弹最佳起爆时机问题的步骤可概括如下:

步骤1 初始化,包括所有浓度检测节点的位置,动态决策范围等相关参数值。开始检测云雾浓度。

步骤2 更新节点运行速度与位置信息,计算此时刻目标函数值。并判断此刻是否满足〈a1,xi〉条件。

步骤3 各个节点向上级汇报判决结果,计算总体目标函数值φ,判断是否达到预期的目标函数值。

步骤4 若算法达到预期的目标函数值,则输出总体目标函数值并发送协同起爆指令,否则,转步骤2继续执行。

3 仿真分析

为了验证多级决策方法对云雾最佳起爆时机的判断性能,基于文献[5]中构造的二次型云爆弹数学模型进行仿真分析。假设该云爆弹战斗部为圆柱体,底面半径r0=0.81 m；高h0=2.18 m。其中装填的液体云爆剂为环氧乙烷(C2H4O),装药质量为700 kg。并且引用文献[5]中,基于量纲分析和π定理与相关试验数据推导得来的云雾扩散半径随时间变化的函数关系为:

(7)

云雾扩散高度随时间变化的函数关系为:

(8)

式(7)、式(8)中，r(t)表示云雾扩散半径,r0为该云爆弹战斗部底面半径；h(t)表示云雾扩散高度,h0该云爆弹战斗部圆柱体高度。e为中心抛撒装药单位质量释放的能量,该云爆弹中心抛撒装药为B炸药,e=3.6×105J；b为中心抛撒装药与云爆剂的装填质量之比b=0.4。

根据云雾的形成过程可知,云雾团的形状是不规则的,不能使用简单的圆柱体积公式来计算,所以计算云雾体积时本文采用文献[6]中的云爆剂体积经验公式:

V(t)=ηπh(t)r2(t)

(9)

式(9)中,V(t)为云雾团不同时刻的体积,单位为m3；η为常数,一般为0.9；h(t)为云雾团不同时刻的高度,单位为m；r(t)为云雾团不同时刻的半径,单位为m。假设云雾中的云爆剂在爆轰前已经全部气化,云爆剂的总体气体百分比浓度为:

(10)

式(10)中,C(t)为云爆剂的体积浓度；M为云爆剂的摩尔质量,单位是kg/mol。则将式(3)、式(4)带入式(5)可得云雾体积随时间变化的曲线图形如图1所示。将式(5)带入式(6)可得浓度随时间变化的曲线如图2所示。

图1 云雾体积随时间变化曲线Fig.1 Curve of cloud volume change with time

图2 云雾气体浓度百分比随时间变化曲线Fig.2 Curve of gas concentration percentage change with time

由以上整体云爆剂特征信息为基础,云雾团扩散形成一个椭球体。各节点通过第一次爆炸,随机分布于云团内进行浓度抽样检测。在引信系统开始工作后,以云雾中轴沿水平方向上的切面可得浓度检测引信节点分布示意图如图3所示。

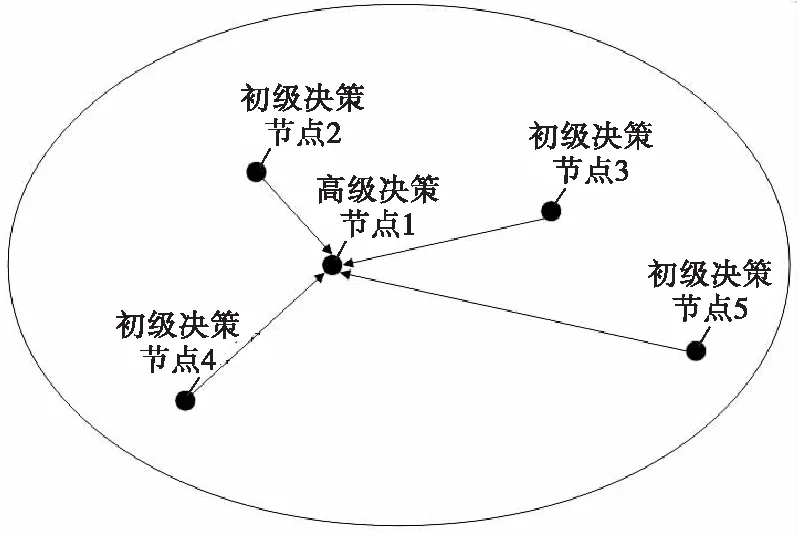
图3 浓度检测节点t0时刻分布示意图Fig.3 Temporal distribution diagram of concentration detection node t0

在抛撒过程结束后,假设检测节点的初始速度为Vi(i=1,2,3,4,5)。

各检测点每100 ms检测一次所在区域云爆剂浓度,浓度值如表1所示。

环氧乙烷的爆轰浓度范围是5%～20%,即当平均气体百分比浓度到达该爆轰浓度范围时,判断此时达到最佳起爆时机。采用式(2)算术平均法计算结果如表2所示。

采用多级决策法对起爆时机判决,云雾爆轰威力分为0，1，2，3，4，5,共六个等级。预期总体目标函数值为等级5,结果如表3所示。

表1 浓度检测统计

表2 算术平均法判决最佳起爆时机结果表

表3 多级决策法判决起爆时机结果表

4 结论

本文提出了基于多级决策的云爆弹最佳起爆时机的判断方法。该方法将浓度检测引信系统分为多个决策层,在一系列递进的决策中逐渐地判断云雾最佳起爆时机。通过仿真分析,对照两种方法判决结果表可以看出:

1) 前300 ms云爆剂浓度分布不均匀,原因在于高浓度燃料气体在此时刻没有向外扩散,仍集中于抛撒范围内部,造成了内高外低的现象。但算术平均值法计算得出云雾团整体浓度均值满足云雾浓度爆轰区间,并判断该时刻为最佳起爆时机,产生误判的现象。而多级决策过程中,由于部分决策节点判断某些区域的局部浓度还不能满足云雾浓度爆轰区间,所以总体决策认为整体云雾团不满足最佳起爆条件。多级决策法判断出了云雾浓度分布不均匀,有效的避免了样本方差过大,而样本均值满足爆轰条件的误判问题。提高了浓度检测引信系统对最佳起爆时机判决的可靠性。

2)当检测时间在800～900 ms之间时,所有决策节点均判断局部浓度满足爆轰威力值时,总体决策判断此时为最佳起爆时机。该判决结果与构造的云爆弹数学模型最佳起爆时机一致,证实了多级决策法对云团最佳起爆时机判决的有效性。

在今后的研究之中,拟建立更详细的云雾扩散过程数学模型,增加决策层级数,对最佳起爆时机做出更加精确的判断。