多样本遗传算法在武器外弹道组网试验中的应用

宫志华， 段鹏伟， 刘洋， 陈春江， 吕海东

(63850部队， 吉林 白城 137001)

0 引言

在武器试验外弹道测试领域，决定和影响外弹道测量精度的因素主要包括：目标飞行弹道特性、外测测量体制、测试设备组成和数量、测试设备布站位置、跟踪几何关系以及弹道参数估计方法等[1]。考虑外弹道测试主要任务是评定和分析武器打击精度，因此测量体制选择和设备布站设计的首要原则是如何可靠跟踪飞行目标并获取目标的高精度弹道参数。通过对测试设备合理布站，可以与被测目标构成良好的空间几何关系，进而使弹道参数测量精度能够达到最优。

为获取最优布站方案，理论上可以在试验区域内，采用剖分网格法对测试设备可能的布站情况进行弹道参数解算精度遍历计算。但是，这种类似穷举遍历寻优计算随着设备数量的增加、试验区域范围的扩大和搜索精度的提高等因素而产生搜索的“组合爆炸”[2]，计算资源不堪重负，效率极低。因此，要更好地应用于工程实际，必须设法降低计算量并能够达到最优的目标。

外弹道组网测试优化布站问题的实质，是对高维度、多峰值非线性目标函数在有限解空间范围搜索极值的问题，是一类典型的非线性约束函数优化问题。传统优化方法对目标函数和约束函数连续及可微性的严格要求使得传统优化方法的应用范围受到极大限制[3]。近年来，通过模拟自然生态机理求解复杂优化问题的仿生人工智能优化算法相继被提出和研究，并在模式识别、机器学习、人工生命等众多领域成功应用，如遗传算法[4-7]、蚁群算法[8-9]、量子遗传算法[10-11]、粒子群算法[12-13]、免疫算法[14-15]、神经网络算法[16-17]以及各种混合算法[18-19]等。从本质上而言，这些智能优化算法的共同点，都是通过模拟或揭示某些自然界的现象和过程来实现对复杂问题的求解，不是一种确定性的数学工具，而是具有自适应调节功能的概率搜索优化算法。

遗传算法是模拟自然界生物进化和遗传规律的一种算法[3]，它采用进化过程中的复制、杂交和变异算子来研究线性和非线性状态空间的所有区域，最终找到或接近最优解，能大大降低计算量，提高计算速度。文献[20]采用遗传算法对导弹航天靶场测控体系众多弹道融合方案寻找最优方案，即对参与融合的冗余测元进行了有效取舍；文献[21]采用遗传算法对多台光电经纬仪交会测量布站方案进行了寻优；文献[22]采用遗传算法对多部测速雷达的布站特点进行了优化研究；文献[23]采用遗传算法实现了对敌雷达网压制时我方多干扰机最优布阵设计。这些应用案例虽然效果明显，但是对遗传算法具有的搜索最优解概率特性并没有突出说明和体现。

本文着重解决的是应用遗传算法思想自适应搜索到测试设备最优布站方案，并聚焦到遗传算法具有的概率搜索特性，通过实施Monte Carlo实验和罚函数检验实现大概率锁定最优解。

1 优化布站遗传算法设计

优化布站所要解决的问题是，在试验场各种实际约束条件下，按照一种或几种目标原则，如测量精度、跟踪能力、作用时间等，进行最优布站，以保证在弹道段落内最大概率地实现所设定的目标。测试设备布站相关的约束条件根据具体要求设定，如试验区域范围、设备基线长度、跟踪角度限制和避开火焰干扰等。因此，优化布站问题可以通过构建一个或多个目标函数及相应约束条件函数(罚函数)来描述，而遗传算法思想就是根据待求解优化问题的目标函数构造一个或多个适应度函数，然后按照一定的规则生成经过基因编码的初始群体，对群体个体(染色体)进行评价、遗传运算(交叉和变异)、选择等操作。经过多代进化，获得适应度最好的一个或几个最优个体作为问题的最优解。因此，本文结合测试设备组网优化布站问题，并聚焦遗传算法概率特性，设计了多样本遗传算法运算过程，如图1所示。

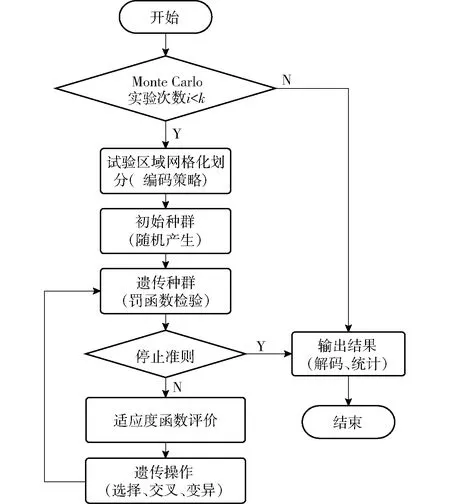
图1 多样本遗传算法计算过程流程Fig.1 Flow chart of multi-sample genetic algorithm

1)编码策略。考虑试验区域范围和搜索精度，将试验区域进行网格化划分，划分原则为

2mx,y,z-1≤(Ux,y,z-Lx,y,z)/kx,y,z≤2mx,y,z，

(1)

式中：mx,y,z为二进制位数；Ux,y,z与Lx,y,z表示试验区域在某三维空间方向(x,y,z)的上限值和下限值；kx,y,z表示网格划分尺度，也体现了搜索精度。基于此原则，测试设备站址坐标是以二进制编码表示，假设n台测试设备组网测量，则位数为n×(mx+my+mz)构成了解空间中的一个染色体。

相反，确定测试设备站址坐标的真实值Px,y,z，即解码的原则为

(2)

式中：gx,y,z为搜索得到的测试设备站址坐标最优染色体。

2)初始种群。在确定初始群体规模数量后，为满足种群的多样性，可随机产生初始种群的个体。在有罚函数的情况下，对于随机产生的初始种群，进行了条件判断，若不满足罚函数的种群个体数大于群体规模的1/3，则重新生成，直到获得合适的遗传种群为止[3]。

3)适应度函数设计。适应度函数是评价群体中个体对环境适应能力的唯一确定性指标，本文将弹道参数测量精度最优设定为测试设备优化布站的目标，则适应度函数设计为可以评价弹道精度的目标函数。

随着武器系统射程增加和测量精度要求的提高，多体制联合测量模式成为必然，弹道解算模型多为联合解算模型，如逐点最小二乘估计(Gauss-Markov估计)、递推最小二乘估计等融合解算方法。特别是，基于动态方程和测量方程联合约束的扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)弹道实时滤波解算技术和基于自由节点样条函数约束(EMBET)的事后弹道融合解算方法等。总之，不论何种弹道模型，都不可能摆脱对设备优化布站的要求。

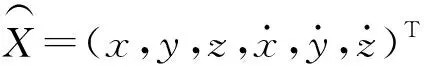
(3)

可写为矩阵形式：

ΔL=A·ΔX，

(4)

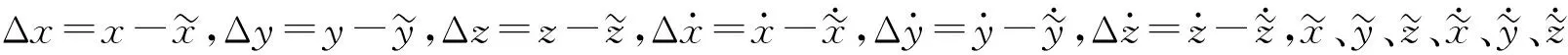
(5)

(6)

式中：0≤α,β≤1，α+β=1，具体确定值依据对弹道坐标参数精度或速度参数精度关注程度而定；M是弹道坐标参数个数；N是弹道速度参数个数。显然，某个染色体的适应度函数最小，说明测试设备按照这样的站址坐标数据进行布站可以确定弹道参数测量精度达到最优。

4)遗传操作。遗传操作是遗传算法的精髓。遗传操作涵盖了选择策略、交叉和变异等操作运算。选择策略采用轮盘赌选择、锦标赛选择和保留精英个体等算法保证了父代种群中适应度高的精英个体能够繁殖到下一代；交叉操作选用单点交叉或两点交叉等算法，得到了新一代结合父代特点的个体；变异选用均匀变异或高斯变异等算法，增强了种群的多样性，使搜索跳出局部最优解。

5)停止准则。遗传算法的停止准则采用设定最大遗传代数或规定的搜索精度等。

6)Monte Carlo实验。遗传算法从初始种群的生成、选择策略、遗传操作等方法，都有概率的因子参与其中，具有全局自适应搜索概率特征，有理论证明[24]，基本遗传算法收敛于最优解的概率小于1. 因此为大概率、可靠地获得全局最优解，在有选择策略的基础上，进行适当Monte Carlo实验，对多个最优解统计分析后可获得全局最优解。

2 实例设计与分析

2.1 实例设计

针对某型武器系统鉴定试验，测试要求是：仅调用1部雷达和2台光学经纬仪测试设备对外弹道进行测试，弹道射程40 km，弹道坐标测量精度≤2 m，试验区域范围≤45 km×8 km. 其中，雷达站固定布设于发射阵地后方，经纬仪机动布设于弹道线下周围。因此，需要解决的问题是：如何对2台光学经纬仪进行布站，并与雷达固定站组合测试获得最高精度的弹道参数。

为接近实际情况，考虑测试设备实际测量水平，在基于理论弹道反算获得各设备原始测元的基础上加入了相应的误差数值，如表1所示。

2.2 计算结果与分析

基于上述多样本遗传算法设计流程，首先对试验区域进行网格化划分，设定设备站址坐标(x1,z1,x2,z2)的实数值用二进制表示，位数均为10，则x轴坐标方向的搜索精度为44.9 m，z轴坐标方向的搜索精度为7.8 m.

确定相关遗传算法参数：随机均匀抽取初始种群大小100个，最大遗传代数50代，采用轮盘赌选择策略，两点交叉和高斯变异操作，交叉概率0.8，

表1 组网测试设备误差值设定

图2 某次实验初始种群分布示意图Fig.2 Initial population distribution in a certain test

变异概率0.1，每代遗传保留2个精英个体。

针对遗传算法概率搜索特性，设定500次Monte Carlo实验，统计所有最优结果，并取大概率解作为最终解。再与传统布站方法比较测量精度，验证解算结果的有效性。

每次实验随机选取100个个体，经过罚函数检验可能会淘汰部分个体。图2是某次实验2台经纬仪布站初始种群示意图，为满足经纬仪基线距离不能小于5 km的要求，实际参与解算的种群数量是86个。从图2中可见，初始种群合理的分布在所有实验场区内，体现了种群的多样性。

只考虑弹道坐标测量精度，即适应度函数(5)式中，α=1，β=0，由遗传算法解算并经过500次Monte Carlo实验后，得到500个经纬仪最优布站解个体，具体分布如图3所示。如果以纵向30 km和横向0 km为分界线，则划分出4个象限，从图3中可见，2台经纬仪都以一定概率分布在这4个象限内，则最优解的象限分布共有16种组合情形，统计最优解象限分布落入次数如表2所示。

图3 500次Monte Carlo实验设备布站最优解分布示意图Fig.3 Optimal equipment disposition solution distribution in 500 times Monte Carlo tests

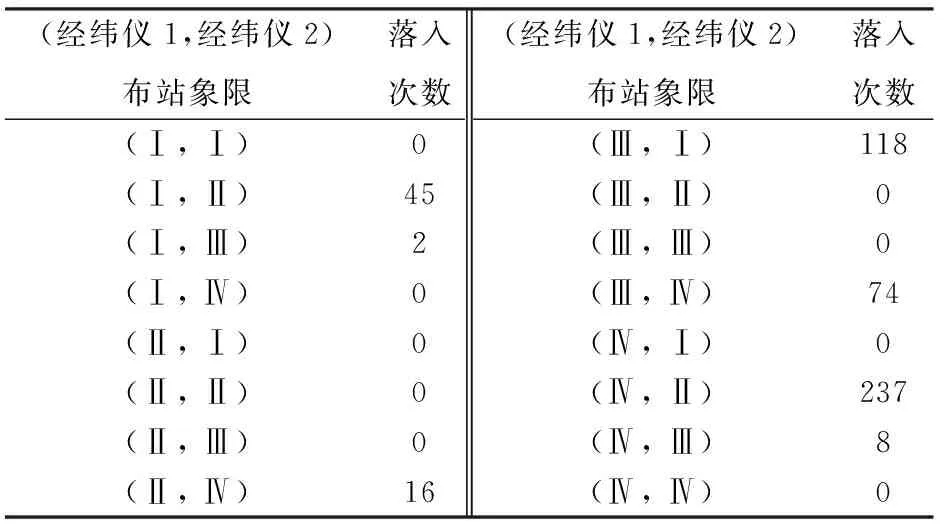
(经纬仪1,经纬仪2)布站象限落入次数(经纬仪1,经纬仪2)布站象限落入次数(Ⅰ, Ⅰ)0(Ⅲ, Ⅰ)118(Ⅰ, Ⅱ)45(Ⅲ, Ⅱ)0(Ⅰ, Ⅲ)2(Ⅲ, Ⅲ)0(Ⅰ, Ⅳ)0(Ⅲ, Ⅳ)74(Ⅱ, Ⅰ)0(Ⅳ, Ⅰ)0(Ⅱ, Ⅱ)0(Ⅳ, Ⅱ)237(Ⅱ, Ⅲ)0(Ⅳ, Ⅲ)8(Ⅱ, Ⅳ)16(Ⅳ, Ⅳ)0

从表2中可以看到，2台经纬仪组合布站最优解落入(Ⅳ，Ⅱ)象限是237次，概率高达47%. 图4是500次Monte Carlo实验最优解适应度函数值分布。其中，最小值出现在第336次实验，2台经纬仪最优布站解所呈现的坐标数值分别是(37 755.5 m，-3 254.9 m)、(12 666.3 m，3 875.6 m)，也确实落入到了(Ⅳ，Ⅱ)象限大概率区域内。

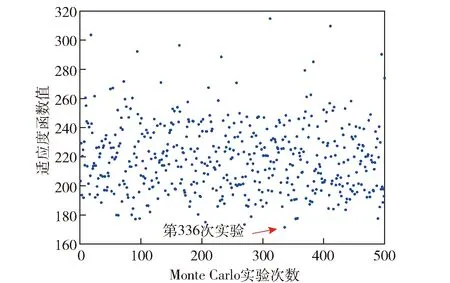
图4 500次Monte Carlo实验适应度函数值Fig.4 Fitness function values of 500 times Monte Carlo tests

为验证所得最优解布站方法的有效性，与场区传统布站方法进行验证计算和比对分析，两种布站方法与弹道的平面几何关系如图5所示。

图5 传统设备布站和弹道平面几何关系Fig.5 Geometric relationship of traditional equipment disposition and ballistic plane

通过计算分析，两种布站方法的三维弹道均方根误差Ex、Ey和Ez如图6所示，其中图6(a)是采用传统布站方法的弹道解算误差，坐标总误差3.400 m，图6(b)是基于最优布站方法的弹道解算误差，坐标总误差2.266 m. 显然，由最优布站方法确定的组网测试方案测量精度高。

图6 两种布站方法测试误差图Fig.6 Test errors of two kinds of disposition method

在工程实际应用中，由于约束条件有限，由计算分析获得的最优布站方案，还需要结合试验场区实际地理环境、数据通讯和后勤保障等条件，在此最优方案基础上适当调整才能有效实施。

3 结论

武器试验外弹道组网测量模式决定了优化部署多部测试设备的重要性，对测试效率和测试成果影响重大。本文提出采用多样本遗传算法思想解决该领域问题，重点关注的是遗传算法本质上具有的搜索特性，为减低遗传算法概率搜索特性影响，有针对性的设计了遗传算法计算流程，其中，重点强调了Monte Carlo实验和种群罚函数检验两种手段。通过列举实例对该方法应用效果进行了仿真分析，得到如下结论：

1)应用本文设计的多样本遗传算法计算流程，能够以近乎遍历的能力得到定量评价优化布站的效果，布站方案效果明显，符合实际需求，避免了定性测试设备布站和简化式理论分析的缺点。在实例分析中可以看到，通过Monte Carlo实验统计结果，测量设备布设在(Ⅳ，Ⅱ)象限，即全局最优解的概率高达47%，但测量设备布设在(Ⅲ，Ⅰ)象限，即局部最优解的概率也接近了24%左右，可见，遗传算法陷入局部最优解的情况并不是小概率事件。

2)对具有多参数、多峰值的优化问题进行求解，由于种群、复制、交叉、变异和进化代数等遗传参数的概率性设计因素，搜索到局部最优解的概率是必然的。为大概率、可靠地获得优化问题的全局最优解，在对遗传算法实际应用中应该适度进行Monte Carlo实验，增大计算样本量。对于解空间维度低、少峰值的目标函数，Monte Carlo实验强度可以降低；对于解空间维度高、多峰值的目标函数，应加强Monte Carlo实验强度。

为提高遗传算法搜索效率，结合其他优化算法，如粒子群算法、蚁群算法等，可以改进和提高搜索全局解效率，这也是今后需要继续研究的方向。