基于磁矩分解的运动舰船磁场模型研究
陈 浩,罗静博,崔桉恺
(海军工程大学 兵器工程学院,湖北 武汉 430000)
0 引言
到目前为止,在水中兵器应用领域,对舰船磁场建模的基本假设是舰船静止停泊在固定方向上,由此导出的舰船磁场是静态磁场,满足拉普拉斯方程[1-2]。采用等效源方法或有限元等方法[3-5],能够精确求解出舰船磁场的数学模型,据此评估舰船的磁性状态,所建模型也能较好地用于测量点附近保持同一航向运动的舰船。舰船的固定磁场在十几天内是不变的,但是其感应磁场却随着航向和航行地点的变化而变化[6],因此,根据单一方向测量数据解出的磁场模型不能用于评估不同纬度、不同航向的舰船磁场。需要掌握舰船的实时磁场状态,便迫切需要建立舰船磁场在实际航行中的数学模型。本文将通过等效源的方法,求出固定磁矩参数和感应磁矩参数。其中固定磁矩是不变的,适应于不同纬度和不同航向,而感应磁矩可以根据不同航向和不同纬度的磁场投影的大小进行调整后精确描述运动舰船磁场的磁性。由此建立舰船磁场能适用于不同航向和不同纬度的数学模型。
1 旋转椭球体与磁偶极子混合阵列模型
舰船磁场建模等效源中最常见的就是偶极子和旋转椭球体[7-8],其中包括:均匀磁化的旋转椭球体模型、旋转椭球体阵列模型、磁偶极子阵列模型、旋转椭球体与磁偶极子混合阵列模型。需根据舰船磁场的产生机理和磁源分布特征来建立数学模型[9]。建模中,采用合理的模型参数描述舰船磁场的分布规律;采用高鲁棒性模型求解方法求解模型参数;同时采用统计检验方法确保所建模型的置信度和模型精度。
如图1所示,舰船磁场可用1个均匀磁化的旋转椭球体和 1列磁偶极子所组成的混合模型所产生的磁场来拟合。旋转椭球体位于舰船吃水面的中心x=0处,长轴2a为舰船长度LS,短轴2b为舰宽WS;1列N-1个磁偶极子均匀布放于舰船吃水面中线上,布放间隔d取为船宽。
布放间隔d为

磁偶极子个数为

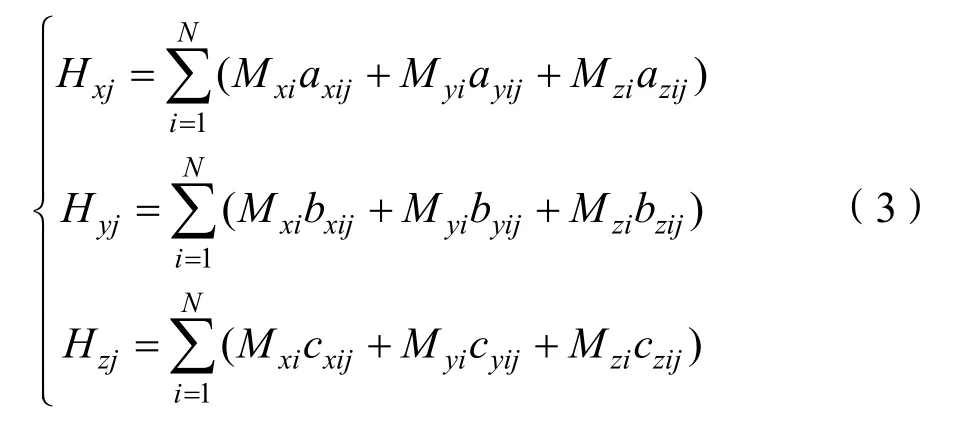
2 考虑航向变换时的模型
2.1 考虑航向变换时舰船磁场建模
在一定的时间内,固定磁性可视为不变,感应磁性,其大小和方向随当地磁场的数值而成比例地变化。所以可以把旋转椭球体或磁偶极子模型的磁矩分解为固定磁矩和感应磁矩进行研究。
根据式(3),利用舰船磁场的测量数据,采用回归方法求解模型参数,得到舰船磁场的单航向模型。
其中每一个旋转椭球体或磁偶极子的解法为

利用式(4)建立关于磁矩的线性方程组如下:

方程(5)有3个变量,3×n×m个方程,属超定方程,一般用最小二乘法求解。为了用最小二乘法求解方程(4),将下标重排,下标重排规则为(11,12,…,1m,21,22,…,2m,…,n1,n2,…,nm,)=(1,2,…,K)其中K=n×m为测量点数目。
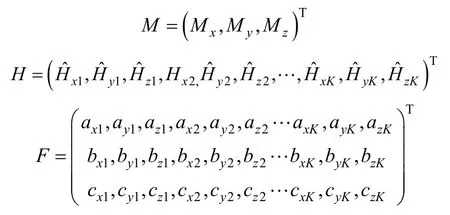
方程(5)的最小二乘问题可用以下方程表示:

由式(7)得到式(8):

式(8)就是方程(4)的最小二乘解,由此计算出磁矩后便可利用式(3)计算出边界面下方任意点的舰船磁场。
如果要求得运动舰船模型,需要把舰船磁场分解成固定分量和感应分量,舰船磁场的模型磁矩也可分解成固定磁矩和感应磁矩,即:

已知,舰船在航行过程中,由于受地磁场感应磁化而形成的感应磁性,其大小和方向随当地磁场的数值而成比例地变化,所以纵轴方向感应磁矩可表示为地磁场纵向方向与比例系数之积。

式中:Kxi为纵轴方向感应磁化系数;BH为地磁场的水平分量;ψ为磁航向角。
将式(10)代入式(9)得到:
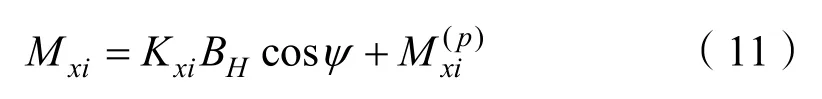
同理可以得到方程:

式中:Kyi、Kzi分别为横向方向和垂直方向的感应磁化系数;分别为横向方向和垂直方向的固定磁矩。这里很显然,BH、ψ均为已知量,只要有2组数据就可以解算出Kxi、Kyi和。由于舰船在横向方向与垂直方向的体积相似,故磁化系数可以近似代替,即:Kzi=Kyi。
于是式(12)可以改写成:
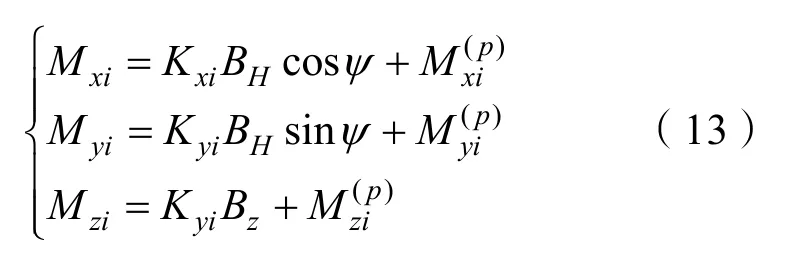
利用 2组模型磁矩参数就可以解算出以上方程的所有参数,利用多组模型磁矩参数平均计算可提高精度。
计算出磁矩后便可利用式(3)计算出边界面下方任意点的舰船磁场。从而得到不同航向上运动舰船的磁场的数学模型。
2.2 运动舰船数学模型计算分析
采用模型舰船的实际磁场数据进行运动舰船数学模型计算分析。舰船磁场分析软件应用线性回归的方法进行旋转椭球体与磁偶极子混合建模,采用14个磁偶极子与1个旋转椭球体来模拟舰船磁场。分别得到4组相互正交的航向上磁矩数据。分别为北(N)、东(E);北(N)、西(W);东(E)、南(S);西(W)、南(S)4组数据。求解,得到4×15 组模型参数Mx、My、Mz。
模型驱逐舰的数据为船长Ls=132 m,船宽Ws=10.8 m,测量深度分别为Z=13 m和Z=22.3 m,其数据点分布见图2。
利用2.1节中描述的方法,求解得到的磁矩方程参数如图3所示。图中仅列出Z=13 m时的情况,Z=22.3 m时结果类似。

图2 舰船磁场测量数据点分布Fig.2 Distribution of measurement data points of ship magnetic field
从4组数据计算出来的参数由15个点组成,从图3-4可以看出其变化趋势相同。要注意的是:图3-4中,参数值最后一组值的参数是旋转椭球体模型参数数据,其x、y轴方向感应磁化系数,x轴方向固定磁矩都明显大于前面14组偶极子模型参数数据。14个磁偶极子数据得到的x轴方向固定和感应磁矩、y轴方向感应磁化系数参数组变化趋势基本相同,有一定的误差,这是由于磁场测量是有一定的误差所引起的。由于初始计算的4组数据是不相关的4个方向数据的正交组合,所以计算结果表明了算法的稳定性。利用多组模型磁矩参数平均计算得到更精确的参数。

图3 X轴与Y轴的固定磁矩与磁化系数(15个模型点;Z=13 m)Fig.3 Fixed magnetic moments and susceptibilitys of X-axis and Y-axis(15 model points;Z=13 m)
将计算得到参数组期望值代入式(13),可得磁矩参数值Mx、My、Mz的解算方程,可计算固定纬度任意航向的舰船磁场,使用模型得到北航向舰船磁场反演数据与测量演算数据进行对比,得到的对比图如图4所示。
从图中可以看出,反演数据与测量演算数据有较好的一致性,可进一步计算相对标准偏差来分析数据精度,采用下式进行计算:

在水深为13 m处测量时计算结果为5.74%,当水深为22.3 m时,相对标准偏差为10.6%,总体精度较高,证明了所建模型的有效性。
3 考虑纬度变换时的模型
在上一节的分析中,得到了考虑航向变化时的舰船磁场数学建模的关键方程为式(13),在方程中引入了磁航向ψ,可以利用方程估算任意航向的舰船磁矩参数,然后利用式(3)解算出舰船的磁场。观察式(12),不难发现BH、BZ已经引入了纬度信息,设θ为舰船航行地区的纬度,可以将式(12)改写成为
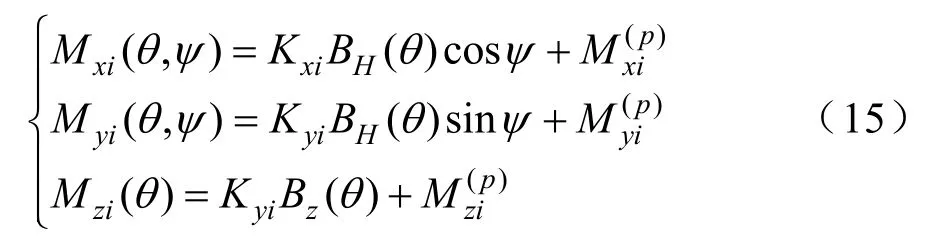
式中θ为舰船航行的纬度。如果知道相同舰船不同纬度磁场测量值是可以计算出Kzi的,故式(13)可以回归到:
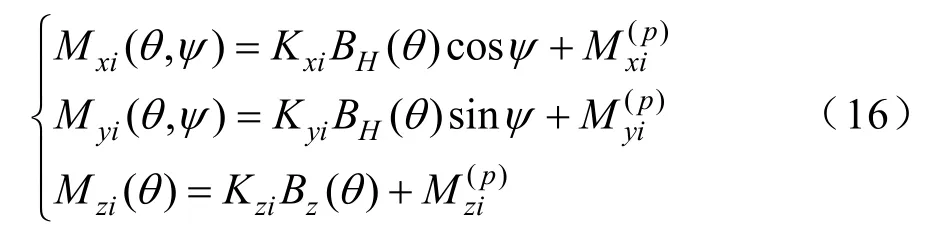
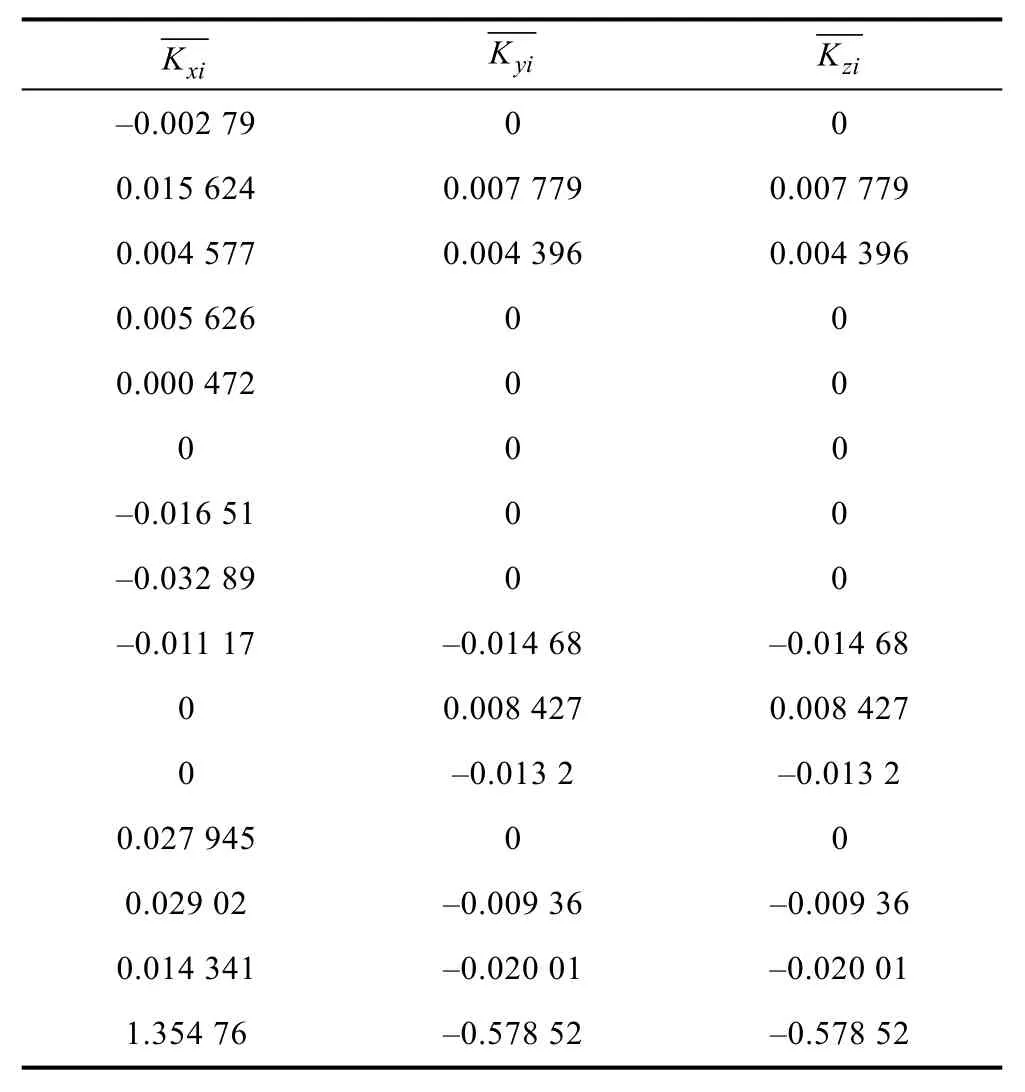
表1 4组数据得到的磁化系数期望值(Z=13 m)Table 1 Expected values of magnetization coefficient from 4 sets of data(Z=13 m)

图4 北航向模型反演数据与测量数据对比(15个模型点;Z=13 m)Fig.4 Comparison of northward direction model's inversion data and measurement data(15 model points;Z=13 m)
4 结束语
本文围绕运动舰船磁场数学建模问题展开研究,分析了舰船磁场的产生来源,将舰船磁场模型参数分为固定磁矩与感磁磁矩,运动舰船磁场数学建模问题主要是针对感磁磁矩进行建模。研究了考虑航向变化和纬度变化时舰船磁场的数学建模问题,采用4个航向的实船数据对建立的数学模型进行了验证,证明了算法的稳定性。分析了现有感应磁场测量方法,并根据磁场测量值得到舰船磁场的计算值,在4个主要磁航向上把舰船磁场感应测量值与舰船磁场计算值进行比较,得出在 4个主要磁航向上进行测量时误差达到最小值的结论,并进一步证明本文提出的运动磁场数学建模的合理性。
与单一航向的舰船磁场建模方法相比,同时建立 4个不同航向的主要困难在于要保证用不同航向测量数据独立解出的4组数据必须相容,由此才能解出感应磁矩和固定磁矩。由于采用等效源方法,最后用最小二乘法来进行计算,所得到的解一般是局部最优解。难以保证独立解出的4组参数相容。为了克服这一困难,在各航向进行舰船磁场建模时采用0.96高置信度水平F统计检验方法对模型参数进行了检验。并对测量数据选取和等效源阵列布设进行了优化,有效保证了不同磁化状态下模型参数求解结果的相容性。

