Lamb波在水下弹性板散射声场仿真实验

赵秀凤，崔海超，董 瑞

（中国人民解放军 91315部队，辽宁 大连 116041）

0 引言

海洋的经济和军事意义非常重要，军事上，控制海洋是打赢现代高技术战争的重要因素之一，水下信息则是反潜战和潜艇战致胜的重要条件之一。目前声波还是唯一能在海洋中远距离传输的能量形式，声呐是利用声波来测量水下目标各种参数的设备。水下目标通常为弹性壳体，入射声波激励产生的散射波中会有弹性散射波，也即弹性壳体中弹性波的漏波。弹性平板中的弹性波以各阶不同振动模态的Lamb波传播，而Lamb波在板端反射会出现模态转换。因此研究Lamb波在板端的模态转换效率是分析水下弹性板的散射声场空间分布的基础，对分置声呐目标识别和探测的研究具有重大的意义[1-2]。

1 Lamb波在水下弹性板散射原理

在水中，某模态Lamb波的临界角为θc，当声波以θc入射到弹性板表面时，会激励出Lamb波在弹性板中前向传播，传播至直角板端E处反射，并且发生模态转换[2]。同时，Lamb波在传播过程中，不断向水中辐射声波，一般称之为Lamb波的漏波。如图1所示。

图1 声波传播示意图Fig.1 Schematic diagram of propagation of sonic wave

某模态 Lamb波的漏波传播方向，由该模态Lamb波的临界角确定，可由公式（1）求得：

式中：θc表示某模态Lamb波的临界角；cw表示水中声速；cp表示该模态Lamb波的相速度。

计算水下弹性板中的Lamb波在直角板端反射后的模态转换效率时，需考虑水下弹性板中Lamb波的衰减系数对其的影响。由于弹性板不吸收声能量，所以当声波在弹性板中传播时，能量会不断地衰减，根据能量守恒定律，弹性板中Lamb波衰减的能量等于其泄漏到水中的能量。

2 弹性板散射声场仿真实验概述

图2 模型示意图Fig.2 Schematic diagram of model

本文利用COMSOL软件[3]，建立了水下弹性板的散射波仿真物理场模型[4]，如图 2所示：中间部分是钢板，长200 mm，厚2.6 mm；钢板四周是水，水域长300 mm，宽100 mm，四周设置有 5 mm的完美匹配层，用来确保声波在自由场内进行传播[5-6]。模型中所选择的材料及其参数见表1。

表1 材料参数Table 1 Material parameters

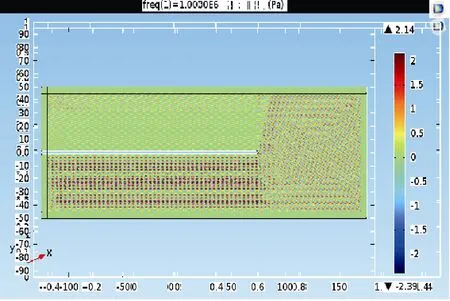
图3 声压伪彩图Fig.3 Pseudo-color image of sound pressure

COMSOL中导出的数据为离散的时域声场，其声压伪彩图如图3所示。从图中体现不出散射声场中波的特征，声场中各阶Lamb波的漏波相互交叠，无法分辨出各阶Lamb波漏波，通过对这些时域信号进行空间傅里叶变换[7]，可以得到 Lamb波的散射波波向量谱图。由于各阶Lamb波的相速度不同[8]，所以通过波数分解可以将不同方向传播的波分离出来，得到不同方向波的强度，得到散射波角度谱图，即可得到漏波的能量。

3 弹性板散射声场构成分析

声波以模态 1临界角入射到水下弹性板表面时，会在弹性板中激励出Lamb波前向传播，传播至直角板端反射并发生模态转换，其散射声场如图4所示，波向量空间如图5所示。

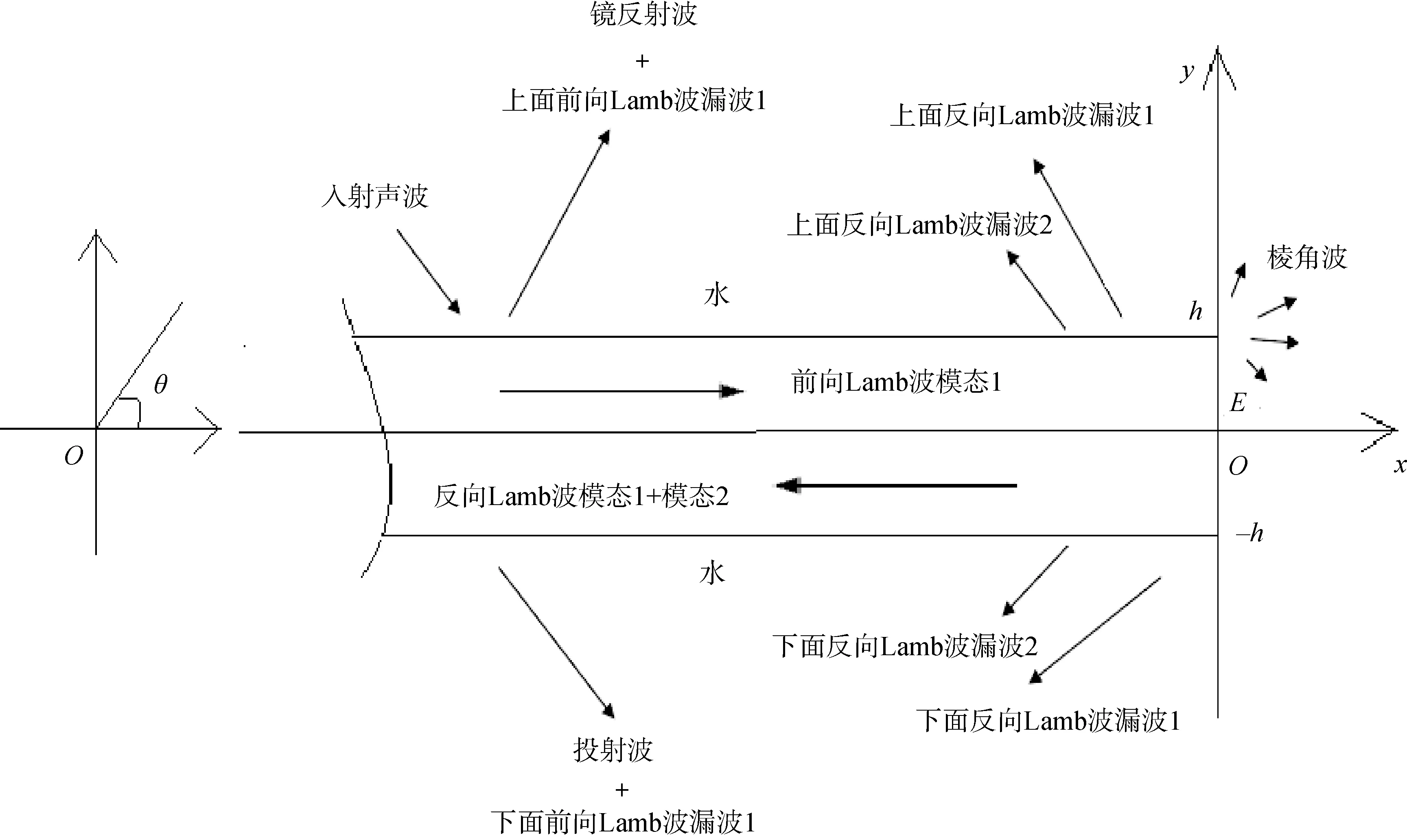
图4 模态1临界角入射、散射声场Fig.4 Modal 1 critical angle incidence，scattering sound field

图5 波向量空间Fig.5 Space of wave vector

4 仿真实验结果及分析

通过公式（1）计算出该模态 Lamb波的临界角[9]，如表2所示。

表2 Lamb波临界角Table 2 Critical angle of Lamb wave

为了更好地研究水下弹性板中Lamb波的模态转换效率，选取以上临界角作为声波的入射角，得到的散射波波向量谱图及散射波角度谱图如图6-7。

图6 A0模态入射，波向量谱和角度谱Fig.6 A0 modal incidence，wave vector spectrum and angle spectrum

图7 A1模态入射，波向量谱和角度谱Fig.7 A1 modal incidence，wave vector spectrum and angle spectrum

已知在频率厚度积为2.6 MHz·mm时，钢板中的 Lamb波存在 3个模态，即A0模态、S0模态及A1模态。当声波以某模态Lamb波的临界角入射到弹性板表面时，声波至少从2个方向出射到水中，我们至少可以观察到2个弹性散射波亮点，由于边界条件对称，因此，在散射波波向量谱图中至少可以观察到4个弹性散射波亮点。本次仿真实验中主要计算A0模态及A1模态的模态转换效率。

从图6-7中可以观察到棱角波亮点、弹性散射波亮点和镜反射波亮点。棱角波在图中为2条清晰的亮线，它们关于横轴对称且相交于横轴，其交点为镜反射波亮点。以临界角入射时Lamb波产生的弹性散射波亮点也能明显的观察到，它出现在棱角波亮线上，这些弹性散射波亮点也关于横轴对称。由于经过板端反射的反向Lamb波形成的弹性散射波和板端形成的棱角波同时到达接收系统，导致弹性散射波亮点出现在棱角波的亮线上。前向Lamb波传播至板端反射后，接收系统会不断地接受到反向Lamb波，由于假设钢板的一端为无穷大，所以接收到的弹性散射波亮点上会出现一条清晰的亮线。声波在钢板的表面不断的反射，接收系统会不断地接受到从表面透射出来的一部分声波，从时间上无法分辨出离散的亮点，所以镜反射波亮点上也会出现一条亮线。

下面我们分析水下弹性板中的前向Lamb波在板端反射后，产生的反向Lamb波各模态能量的转换效率[9]。

设弹性板的表面积为常数s，则有：

根据能量守恒定律：

式中：E兰1为入射波以模态1的临界角入射时激发出的前向 Lamb波在板中的能量；E镜为入射波的镜反射波；E透为入射波的透射波；E上漏1和E下漏1均为前向Lamb波的漏波；V为板端棱角波，在这里我们假设V为小量忽略不计。

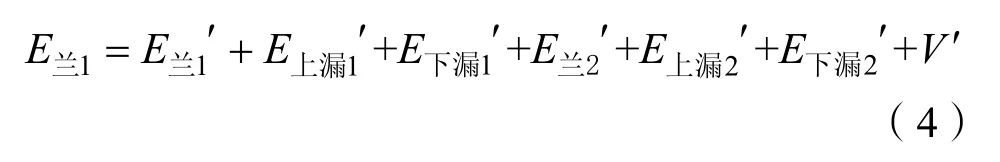
式中：为与前向Lamb波模态1相同模态的反向Lamb波模态1在板中的能量；为前向Lamb波在板端反射后，发生模态转换时，另一模态反向Lamb波模态2在板中的能量；为反向 Lamb波模态 1的漏波；为反向Lamb波模态2的漏波；V′为前向Lamb波在板端的透射波，假设为小量忽略不计。

定义不同模态Lamb波的漏波系数分别为η1和η2，则漏波与Lamb波有如下关系式：

由于入射波能量不变，只是改变了入射角，所以我们假设以相邻非临界角入射时的镜反射波和透射波大小近似等于以临界角入射时的镜反射波和透射波大小，则用临界角入射时的镜发射波、透射波和前向Lamb波漏波之和的能量减去非临界角入射时的镜反射波和透射波的能量就近似等于前向Lamb波的漏波大小，即：

式中：为非临界角入射时的镜反射波；为非临界角入射时的透射波。

由公式（2）-（5）得：

定义前向Lamb波在板端发生模态转换时的模态转换系数分别为φ1和φ2，则有：

基于以上的分析，由空间散射波角度谱可以得到各阶散射波的最大声强幅值，取有效值I则不同角度时的能量为

已知入射波的声强为

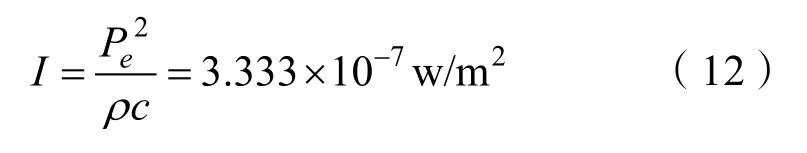
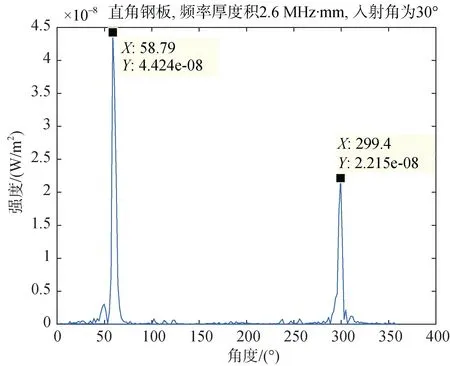
图8 A0模态非临界角入射，角度谱Fig.8 A0 modal non-critical angle incidence，angle spectrum

在水下，当声波以A0模态 Lamb波的临界角入射到弹性板的表面，激励出A0模态前向 Lamb波在弹性板中传播至板端反射后，A0模态和A1模态反向Lamb波的转换效率计算如图8。

表4 前2阶Lamb波漏波系数Table 4 Coefficients of first 2 orders' Lamb wave leakage

表5 前2阶Lamb波在板端的转换效率Table 5 Conversion efficiency of first 2 orders' Lamb wave at end of plate

在水下，当声波以A1模态 Lamb波的临界角入射到弹性板的表面，激励出A1模态前向 Lamb波在弹性板中传播至板端反射后，A0模态和A1模态反向Lamb波的转换效率计算如图9。

从表9中可以看出Lamb波在水下弹性板直角板端发生模态转换时的转换效率仿真实验值与已知论文的理论计算值[10]误差率分别为 9.53%和5.49%。分析误差的来源主要有以下几方面：首先，在仿真实验中划分的网格数量不够精细，导致数据采样点数减少，分辨率降低；其次，空间傅里叶变换时存在频谱泄漏的现象；再次，在分析数据时，不同波之间做的是相干叠加，使得数据的准确度下降。

图9 A1模态非临界角入射，角度谱Fig.9 A1 modal non-critical angle incidence，angle spectrum

表6 波的能量Table 6 Energy of waves

表7 前2阶Lamb波漏波系数Table 7 Coefficients of first 2 orders' Lamb wave leakage

表8 前2阶Lamb波在板端的转换效率Table 8 Conversion efficiency of first 2 orders' Lamb wave at end of plate

表9 Lamb波转换效率对比Table 9 Comparison of conversion efficiency of Lamb waves

5 结束语

本文结合Lamb波在水下弹性板散射原理，以Lamb波的反对称模态为例，通过 COMSOL软件进行了仿真实验，根据能量守恒定律，推导了Lamb波在水下弹性板直角板端反射并发生模态转换时的模态转换效率计算公式，量化了实验结果，并与已知论文的理论计算值进行了比较。