基于遍历噪声修正的测速优化算法
程国胜,李彩菊,李 超
(中国船舶重工集团有限公司第七一〇研究所,湖北 宜昌 443003)
0 引言
多普勒计程仪(Doppler Velocity Log,DVL),也被称为测速声呐。它是迄今为止应用最广,也是最为成功的舰船自主导航设备之一。这种计程仪可测出船相对于地的绝对速度和相对于水层的速度,该类设备测速精度高,在国内外的舰船得到了广泛应用[1]。多普勒计程仪主要工作方式是向海(河)底斜向发射窄带窄波束声波,接收海底反射回波信号,测量出回波信号的多普勒频移。多普勒频移与舰船的绝对速度存在着确定的对应关系,测频精度的高低直接决定了舰船速度测量的精度。对工作深度在数千米的多普勒计程仪来说,能够在较低信噪比下进行频率测量会给设备系统设计带来很大的便利[2]。
多普勒计程仪测速的关键是频率测量。目前已有多种测频方法,例如,过零点检测法、复相关法、快速傅立叶变换法及脉冲对相关估计法等。复相关法在工程上最常被使用,它利用谱矩理论来估计瞬时频率,即估计接收信号功率谱密度的一阶矩和二阶矩[3]。该方法具有运算量小,精度高等优点,但是对信噪比要求比较高[2,4],低信噪比情况下,随着信噪比降低,测频和测速精度快速下降。针对该问题,本文提出了一种基于遍历噪声修正的测速优化算法,性能仿真结果表明,该方法能有效减弱噪声对测速精度影响,尤其在低信噪比的情况下,能有效提高多普勒测速精度。
1 复相关测频算法原理
复相关算法的主要思想是确定两段回波信号之间的幅值和相位关系,从而确定两段回波信号之间的频率。从功率谱的观点出发,多普勒频移测量的问题就转化为确定观测信号功率谱密度的一阶矩[5]。
设一被测信号(不包含噪声)为s(t),其功率谱密度为S(f),它的矩即为平均频率,表示为
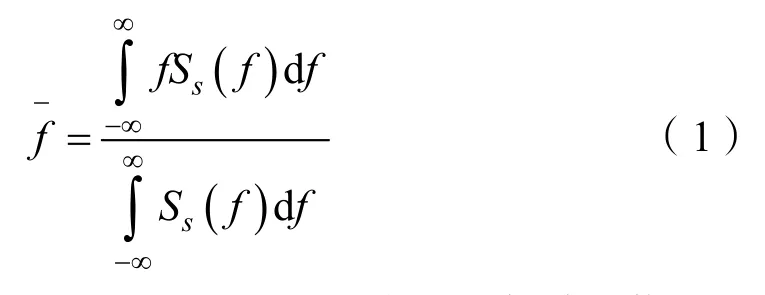
由随机过程的有关知识知道,功率谱与信号的自相关函数R(τ)之间满足一对傅里叶变换的关系:
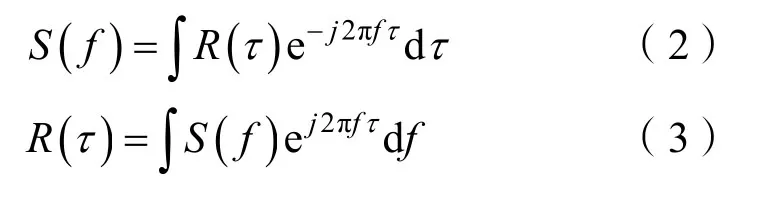
对相关函数求导,并令τ=0,得到:
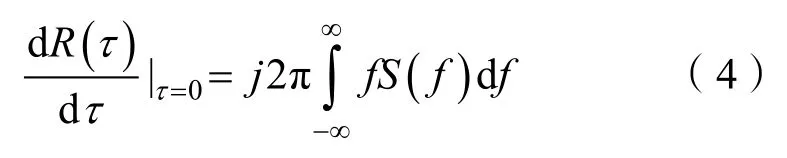
又因为:
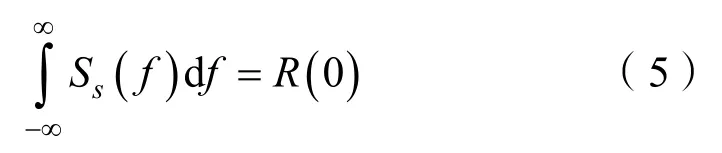
将式(4)和式(5)代入式(1)得到平均频率与相关函数的关系:
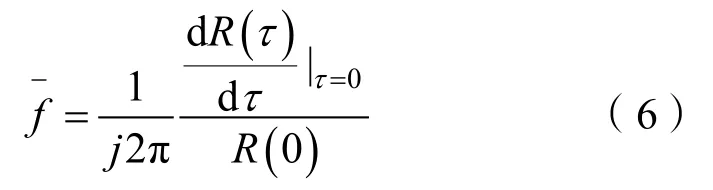
将信号的自相关函数R(τ)表示成极坐标的形式:
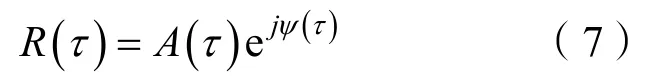
式中:A(τ)为幅度,它是τ的偶函数;ψ(τ)为相位,是τ的奇函数。因此有:
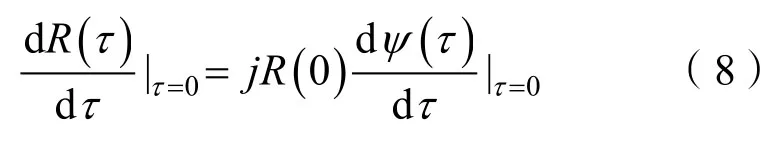
将式(8)代入式(6),得到平均频率:

式(9)说明可通过相关函数的相位在τ=0的导数来求得频率估计。因ψ(0)=0(ψ(τ)为奇函数),所以,该导数值在一个小的τs≠0附近可近似表示为
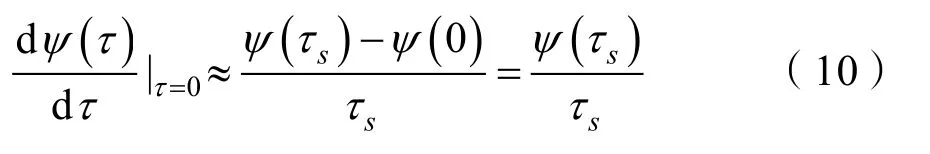
这里τs为采样间隔。将式(10)代入式(9),得到平均频率的估计值:
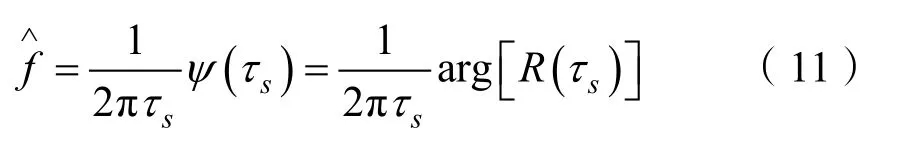
R(τs)为相关函数在τ=τs的值,它可用相邻两样本的共轭乘积之和来表示,即:
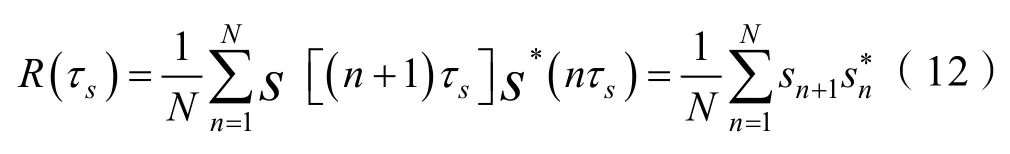
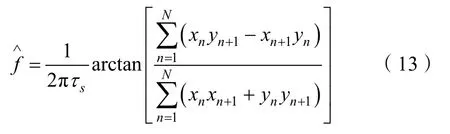
式中,分母上两项分别为复样本的实数分量和虚数分量的自相关,而分子上的两项则为复样本的实数分量和虚数分量的互相关[6-7]。

2 遍历噪声修正
式(13)所表述的复相关测频算法是建立在噪声相关性很低,进而可以忽略的前提下的。然而在低信噪比条件下,噪声的相关性几乎可以与信号相比,如果再忽略噪声,则将带来较大误差。为提高精度,必须对噪声带来的误差进行修正。
当存在噪声时,此时的输入由信号和窄带噪声构成,表示为
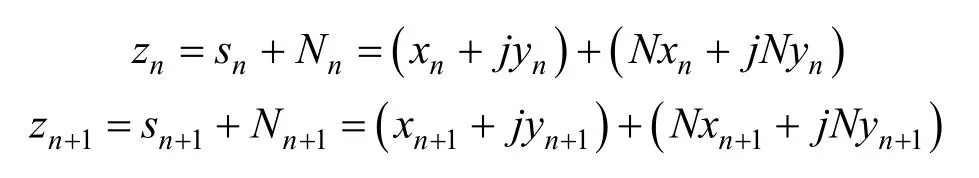
在信号与噪声不相关的情况下,容易得知频率估计值为
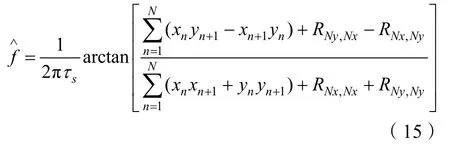
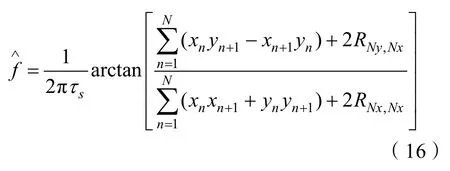
由式(16)容易看出,当存在噪声时,利用复相关测量平均频率将受到Nxn和Nyn的自相关函数和互相关函数的影响,从而带来测频误差。如噪声可测,则可通过测量的噪声计算噪声实部和虚部的自相关和互相关值[8],然后在式(16)中进行修正。在实际中,在具有信号的时间段内,噪声是不可测的。对于高频声呐来讲,海洋环境噪声和舰船自噪声往往要远低于系统的电噪声,因此,系统电噪声将是影响多普勒计程仪性能的主要因素。电噪声通常被认为具有遍历性,所以,噪声的相关性可以用不存在信号的时间段内的噪声计算得到。
将遍历噪声修正后的多普勒频移带入多普勒速度计算公式(14)得修正后的多普勒速度。
3 性能仿真
3.1 基于复相关测频原理的测速性能仿真
仿真条件:设发射信号频率f0=150 kHz,速度V=2 m/s,脉冲宽度为 20 ms,取声速c为 1 500 m/s,带通采样频率Fs=200 kHz,带通采样后的数字带通滤波器中心频率50 kHz,带宽48.5~51.5 kHz。根据分析可知,多普勒频移真实值为 200 Hz,在接收波束形成后的信号中加入高斯白噪声,根据测频公式和测速公式,在不同信噪比下测得的多普勒频移估计值与真实值比较、测频相对误差曲线和速度相对误差曲线分别如图1-3所示。每个信噪比条件下仿真100次取平均。
由图可知,基于复相关测频原理的测速性能受信噪比影响较大,在低信噪比时,测速精度明显降低。
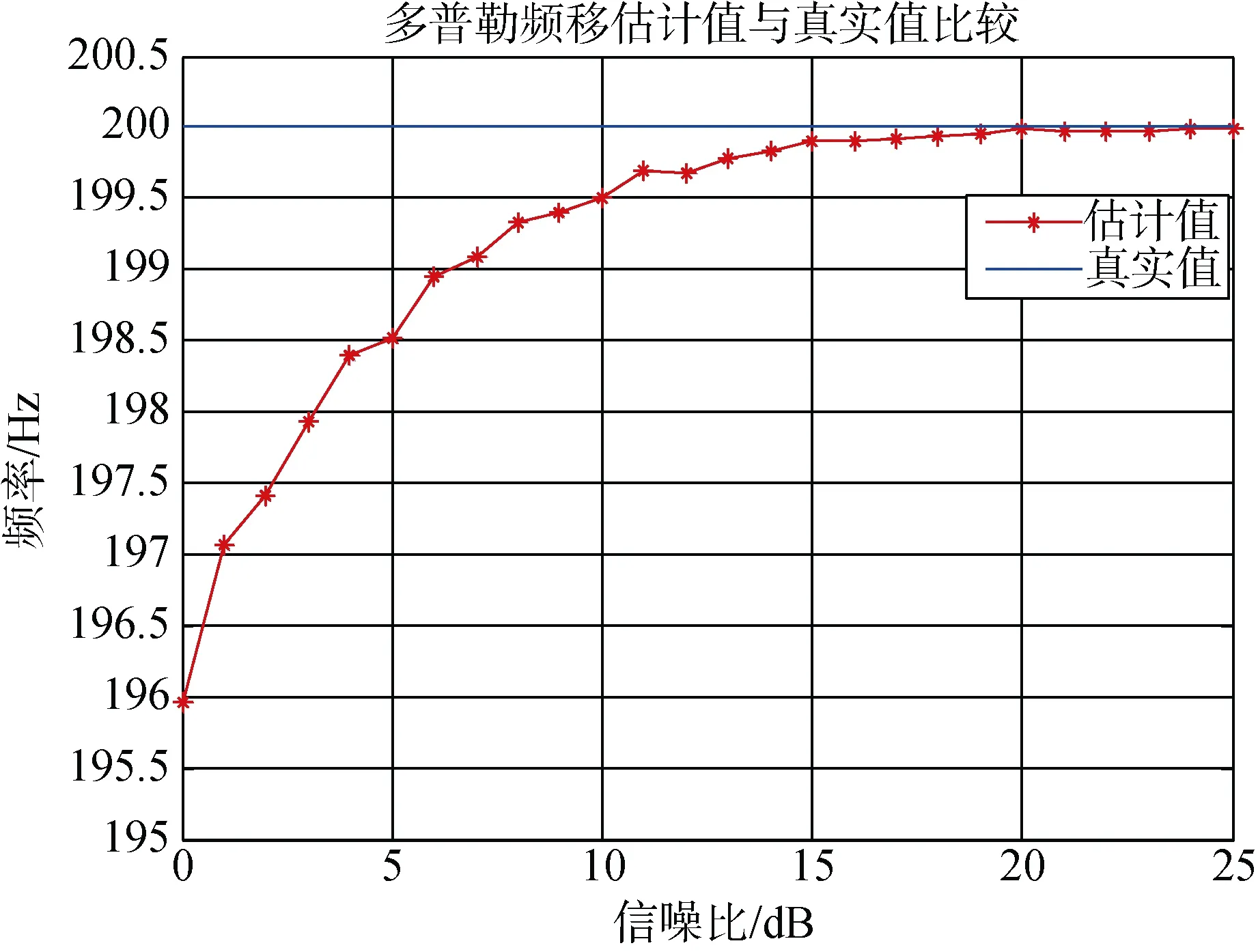
图1 多普勒频移估计值与真实值比较Fig.1 Comparison between estimation and true value of Doppler frequency shift
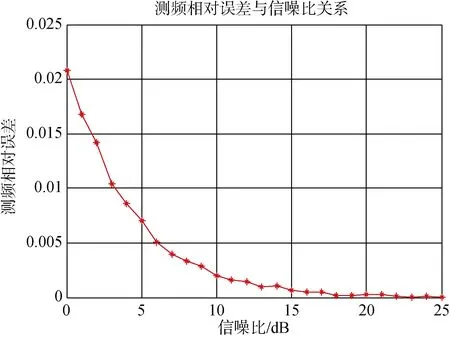
图2 测频相对误差曲线Fig.2 Frequency measurement relative error curve
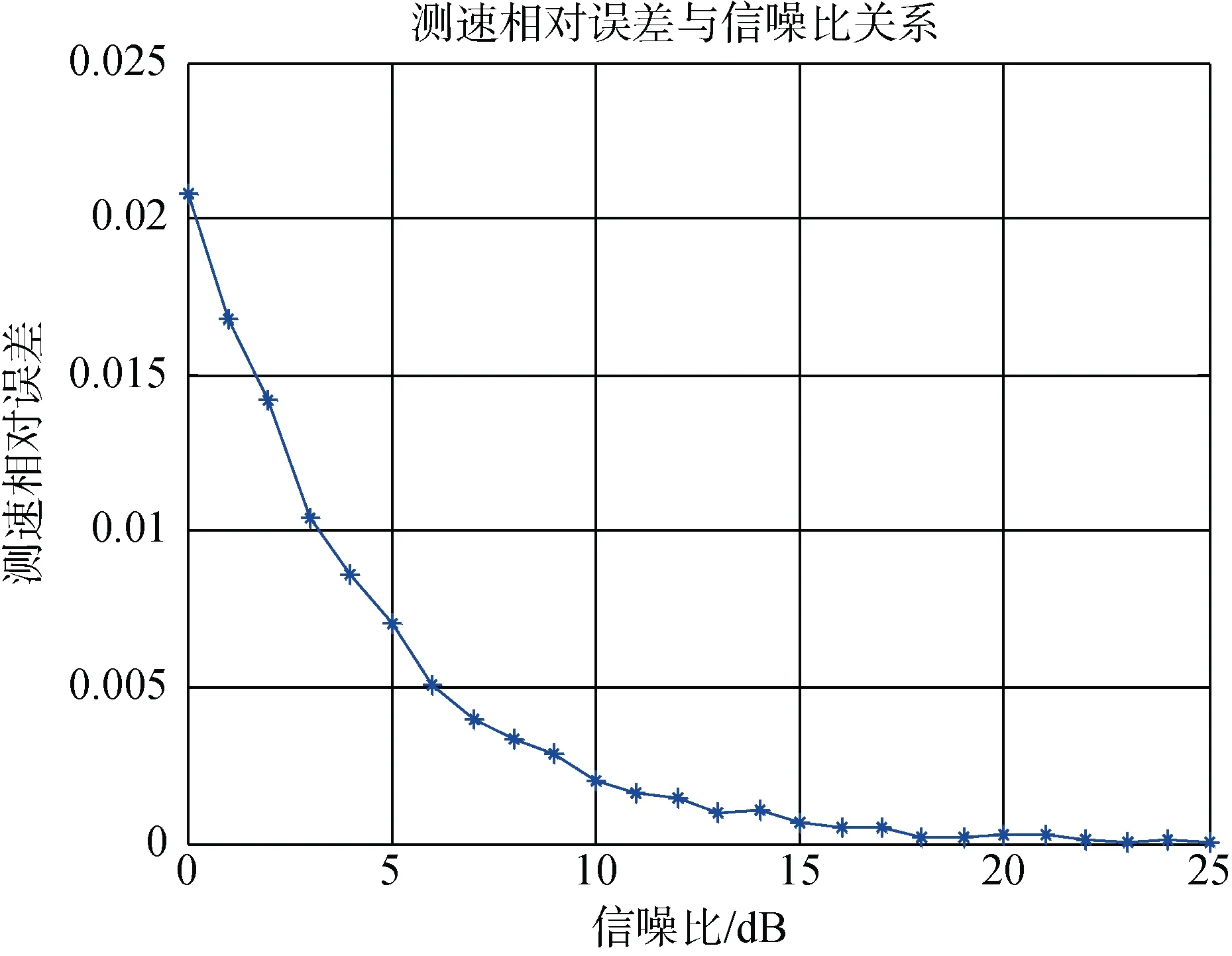
图3 测速相对误差曲线Fig.3 Velocity measurement relative error curve
3.2 基于遍历噪声修正的测速优化算法性能仿真
为了采用噪声修正,我们对噪声进行了分析,认为噪声满足遍历性的条件,可用回波信号时间段之外的纯噪声代替实际的噪声并代入测频公式中进行计算,得到优化后的速度。
仿真条件同3.1节中的条件,分别采用回波信号时间段内噪声和信号时间段外噪声分别进行算法修正计算,计算结果如图4所示。
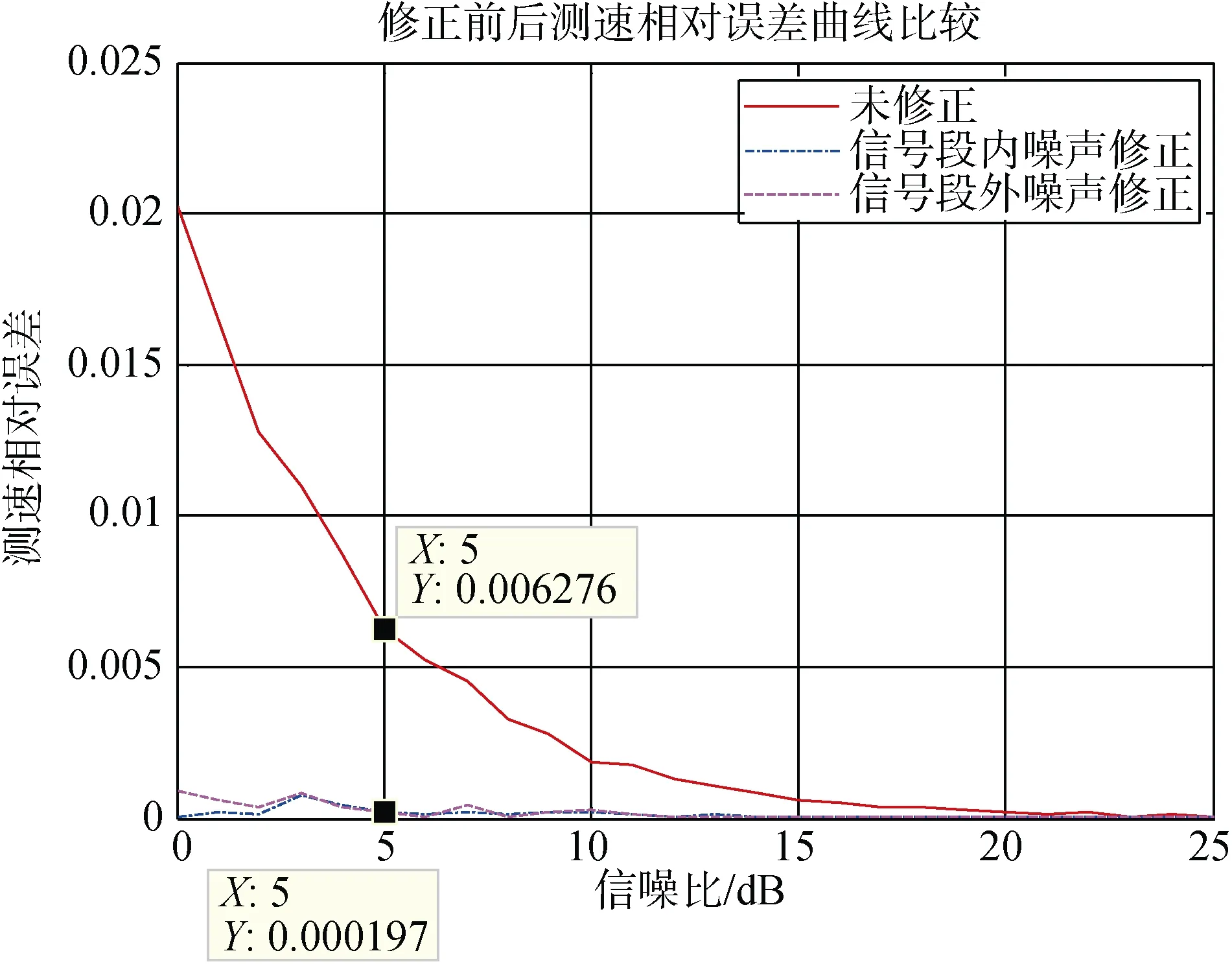
图4 遍历噪声修正前后测速相对误差曲线比较Fig.4 Comparison of relative error curves of velocity measurement before and after ergodic noise correction
从图4中可以看到,在信噪比较低情况下,采用遍历噪声修正后,测速精度明显提高,在信噪比5 dB以内,进行噪声修正后,测速精度提高至少1个数量级。另外,从图中可以看出,采用信号时间段内的噪声和信号时间段外的噪声进行测频修正的效果是基本一致的,这也证明了噪声具有遍历特性的论断。
4 结束语
本文对基于复相关测频原理的多普勒测速算法进行了分析与仿真,并提出了一种基于遍历噪声修正的测速优化算法。仿真结果表明:基于复相关测频原理的测速算法性能受信噪比影响较大,在低信噪比时,测速精度较低。采用遍历噪声修正能有效减弱噪声对测速精度影响,在信噪比5 dB以内,测速精度提高1个数量级以上。由仿真结果可以看出,该算法具有很好的工程应用价值。

