土工试验教学中如何培养学生的不确定性思维
吴兴征 方有亮 余莉 冯震 杜二霞
摘要:土力学试验中测得的土性指标具有较大离散性,导致学生对试验结果缺乏信心。因此,有必要探讨如何在土工试验教学中培养学生的不确定性思维。为提高教学效果,结合统计语言R的绘图和科学计算功能,阐述土性指标统计特性。以颗粒分析、含水量、液塑限、渗透系数、压缩系数和剪切强度指标的多组平行试验结果为例说明不确定性的表述方法。采用概率密度分布曲线、非参数核密度估计、直方图、箱线图等对测试结果进行不确定性展示。该教学实践可以提高学生处理差异数据的综合判断与归纳能力。
关键词:土性参数;不确定性;土工试验;R语言
中图分类号:G642423;TU473 文献标志码:A 文章编号:1005-2909(2019)03-0122-09
土力学试验是土木工程专业本科生的实践课程之一,主要通过测试土的物理性质及在荷载作用下土体的应力变形特性,帮助学生认识和掌握土力学的基本内容。作为实际工程设计的基础数据,土性指标可分为两类:物理特性指标和力学特性指标。前者如土的天然含水量、密度、土粒比重、颗粒组成和液塑限等,后者如土的压缩系数、粘聚力、内摩擦角和渗透系数等。
有别于钢材和混凝土等建筑材料,土体作为一种非人工制造的材料,是长期自然风化与沉积的产物,多为不均匀的三相体。其物理力学性质非常复杂,测试结果的不确定性较大。即使采用同一土料,运用相同的试验方法和仪器,不同的学生也会给出不同的测试结果。这些离散化的结果往往让学生感到困惑,进而质疑土力学试验的科学性和严密性[1]。
结合近年来土力学试验课的教学实践,探讨如何在土工试验教学中培养学生的不确定性思维。在教学中,有意识地向学生强调和说明土工试验的离散性特点,培养其归纳与判断能力。
一、土工试验成果的特点
在室内进行的土力学验证性试验,由于教学时间所限,每个学生仅能完成2~3个平行试验。与同组其他组员的试验结果对比后,会发现大家的试验结果各异。若将全班学生完成的试验结果作为总体样本来分析,可探究土工参数(或土性指标)的不确定性。造成参数离散的主要原因包括[2]:
(1)受到土体应力历史、水力学环境、结构性及化学组成等因素的影响,不同空间位置、不同地质埋深的土性指标有差异,有时甚至相当显著,这是土体的固有变异性。其大小很难通过增加试样个数、提高试验技术和改进设备来降低。
(2)在取样或制样、运输过程中的扰动,以及试验仪器、操作方法和测试习惯的差异,会导致测试结果不同。这是试验不确定性,可通过提高测试技术水平和改进试验仪器来减小。
(3)少量的样本难以真实描述整个场地的土体物理力学性能,测试结果与“真”值或理论值有偏差,可称为统计不确定性。也就是说,较少的室内试验次数难以再现整个建筑场地的实际情况。统计不确定性的数值随着试验数量的增加而减小。
可见,学生在面对具有较大离散性的试验结果时,其传统的绝对确定性观念不同程度地受到冲击。学生在认识不确定性的基础上应形成一种强调差异和统计的思维模式,这里称为“不确定性思维”。
二、土工试验教学中不确定性思维培养
在土工试验教学中,要协助学生分析试验结果的差异,并着力培养学生对规律性的把握能力。可从以下三方面入手培养学生的不确定思维能力。
(1)鼓励学生如实记录试验过程中得到的所有结果,以便确定其可能的最大或最小范围。也就是说,不要轻易放弃自己的试验结果,更没有必要出现沮丧情绪,鼓励学生提出自己的意见来解释试验差异。在明确不确定性的来源后,即便试验结果与理论值(统计均值)有较大偏离,也要尊重试验数据。只要把原因解释透彻,都是满分的答卷。
(2)教师要说明室内试验的量测总是有限的。通常,实验工程师在多年经验积累的基础上,采用适当的统计方法(稍后论述)定量描述参数的不确定性,提供给设计人员合理的统计值区间进行工程安全复核。要引导学生深刻理解这样一个过程,为将来顺利过渡到岩土工程师做好准备[3]。
(3)从减少不确定性的角度出发,要求学生尽量控制量测精度,降低试样的扰动,在时间允许的情况下尽可能对同一样本进行多组平行试验。
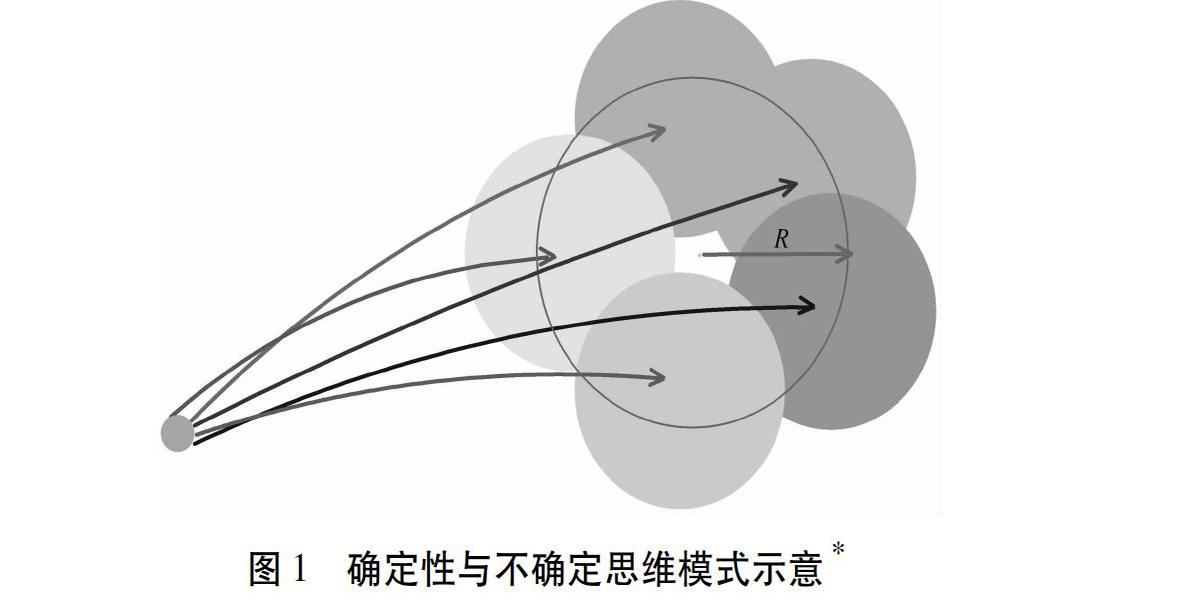
可见,不确定思维方式打破了“若采用A土样必有B结果”的传统思维方式,是与统计决定论相联系的。同样采用A土样,测试结果并不唯一。换句话说,新的思维方式需要实现由一个确定的成果点(值)到特定的不确定成果值域(落入半径为R的区域)的认知转变,如图1所示。不确定思维是学生在多种因素下对土工测试结果处理的理性选擇。随着对单一测试样本的深入分析与多个样本的汇总整理,测试者与试验数据之间的适应关系也会发生转变。比如,依据这些离散性的测试结果,实验技术人员可探究离散性的主要影响因素和统计规律,从而改进与优化试验仪器和测试技能。以下,将通过统计与绘图处理软件,展示土工试验数据的统计特征与教学实践。
三、基于R语言的土工试验教学实践
(一)土工试验的成果整理技术
(1)对于综合性的土体力学特性指标(如粘聚力、内摩擦角和压缩系数等),需要在不同应力条件下通过图解法或最小二乘法确定。比如,辛军霞等人[4]将测试值与预测值间的最小残差平方作为最优回归模型的评估标准,通过非线性规划方法,建立了求解多个描述三轴试验强度包线的数学模型,此不赘述。
(2)工程实际中,土工测试指标多采用平行试验来避免大的误差。在时间有限的教学过程中,可以将不同学生或组别的试验看作平行试验。依据相关技术标准或规范[5],描述测试结果的离散程度,可给出多次测定值的平均值μ、标准差σ和变异系数Cv=σ/μ。
(3)对特定指标的各种概型分布进行拟合优度检验,比如,边缘概率分布和联合概率分布,识别测试结果的最优拟合,以便为土工可靠性分析提供基础数据。
(4)借助简单的图形将数据的离散性直观地展现出来,使学生洞悉看似眼花缭乱的数据中隐含的规律。为展示统计图形在不确定性数据分析中的潜力,可采用概率密度分布曲线、非参数核密度估计、累积频率直方图、箱线图等现代统计图形,力求实现一图胜过千言之目的。
(二)R语言的适用性与优势
R语言是免费、开源的统计分析软件,具有较强的作图功能[6]。与其他编程语言相比,R代码可读性强,具有大量的功能包,涵盖众多领域的函数接口。在岩土工程领域,国内外相关学者发布了土工分析[7]和土工不确定性分析[8-9]的工具包。随着大数据时代的到来,土木信息化水平提高,作为数据处理平台的R语言将有更大作为。
在土工试验教学中使用R语言进行数据处理,可以便捷地展示与整理试验结果,以提高教学效果。比如,多个平行试验的均值和标准差分别可由mean( )和sd( )函数来计算。这些数据的散点图可由R中的plot( )函数绘制,其频率分布直方图可采用hist( )函数得到,箱线图可由boxplot( )函数实施。多种概型分布形式(如对数正态、Gamma、Gumbel和Weibull分布)的拟合优度检验可在R中实施[9]。
土性指标间多具有相关性,比如密度与剪切强度、粘聚力与内摩擦角、液限与渗透系数等,Wu[9]给出进行相关性分析的R语言实施方法。此外,有关土工参数确定时采用的最优回归模型,可参见相关文献[4]。
(三)实例分析
结合土工测试数据深入说明成果整理技术的应用,以便让学生清楚区分统计图形运用的条件和场合。
1.颗粒分析
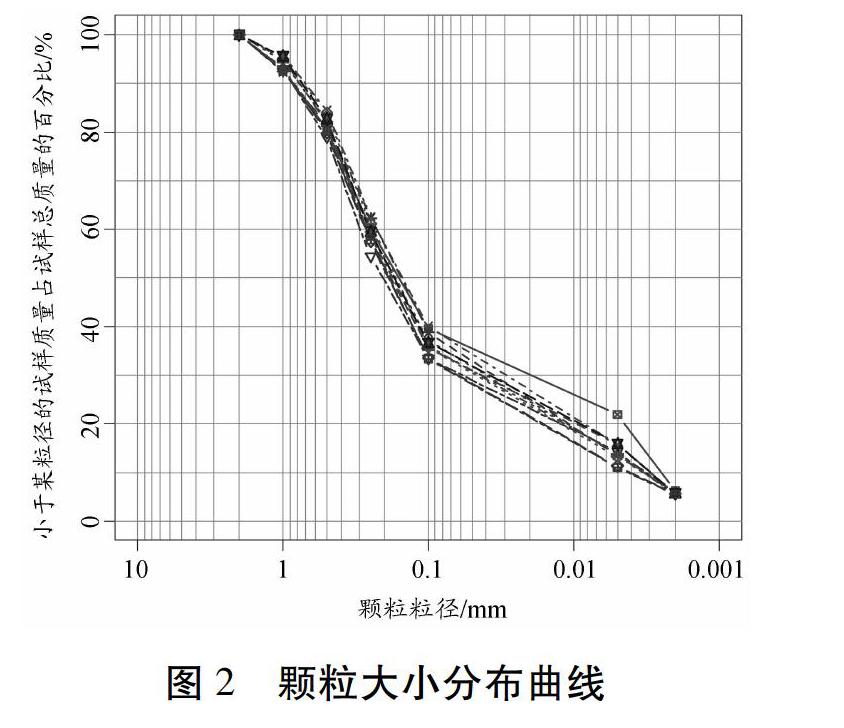
颗粒分析试验主要测定土中各种粒组含量占该土总质量的百分数,并据此绘制颗粒大小分配曲线。图2给出南非Stilfontein小城附近壤质砂土12个样本的测试结果[10]。各级配曲线间略有差异,即相同粒径下小于该粒径的土颗粒含量不一。由于同一百分比量值下对应的土颗粒大小不尽相同,该土体也会得到多个不同量值的曲率系数和不均匀系数。这种离散性可由试验样本选取、颗粒结构组成与粒度分散等因素决定。
2.含水量
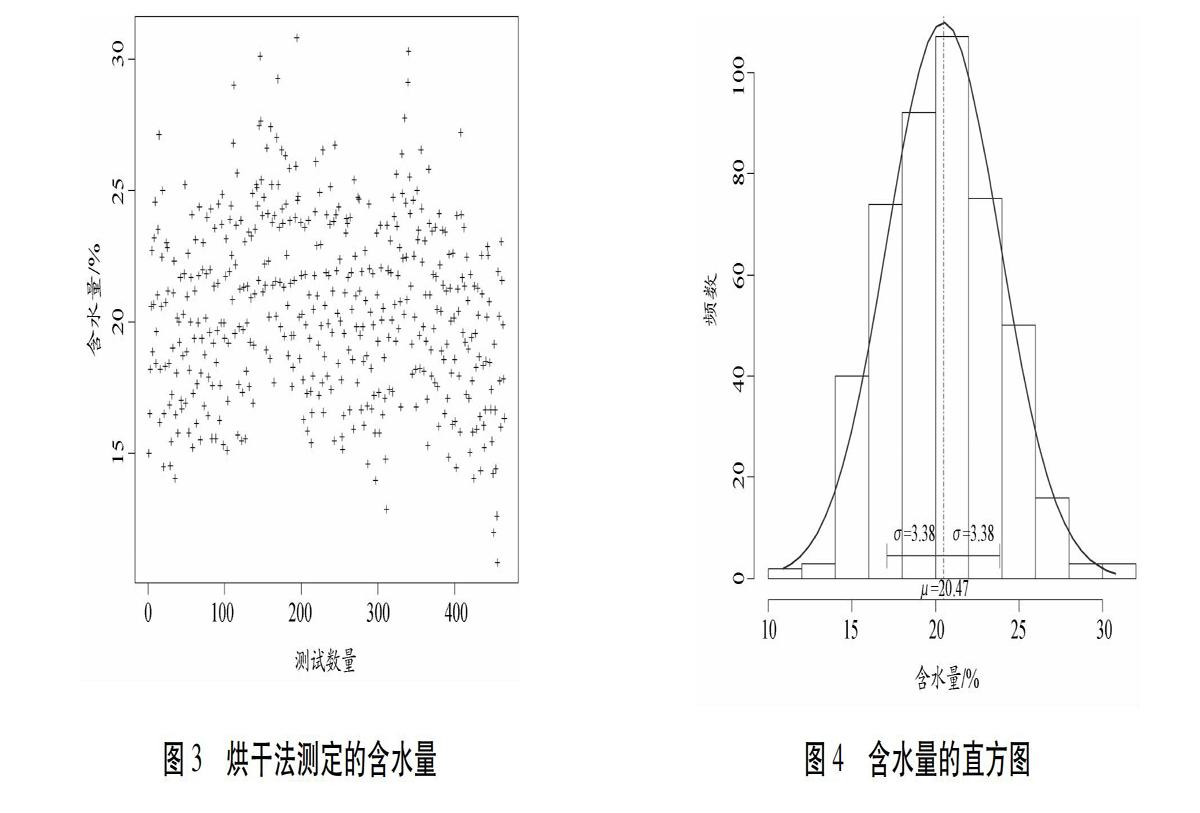
以李祯祥和赵寿刚[11]给出的填筑土料含水量试验为例来展示统计分析结果。这些研究者使用的土类主要为粉质壤土和粉质粘土,采用烘干法测定的数据共计465个。图3给出含水量的散点。可见,含水量的差异明显,最大值为30.79 %,最小值为10.86 %。土体含水量具有离散性的原因为[11]:(a)试验用土量差异;(b)试验用土的类别有异;(c)土样中的有机质含量差异;(d)称量过程中的误差等。
这些含水量的算术平均值μ为20.47 %,标准差σ为3.38 %,计算得到的变异系数Cv为0.16。图4给出含水量的频率直方图。同时给出正态分布的概率密度曲线,其与直方图的轮廓线吻合较好,可直观判定含水量值服从正态分布。更为深入地,可探讨这些数据的非正态性[12]。
3.液塑限
液限和塑限是表征粘性土状态转变的界限含水量,可用于细粒土分类和重塑土软硬程度的判别。采用液塑限联合测定仪给出含水量与锥入深度之间的数据后,确定土体的液塑限需要在双对数坐标系下建立线性回归关系。圆锥下沉深度2 mm对应的含水量值定义为塑限,而下沉深度17 mm对应的含水量值定义为液限[5]。
图5给出Bandung粘土的锥入深度范围为5~28 mm,7组土样,共计39个数据点[13]。最终得到每一组圆锥下沉深度与相应含水率之间的直线关系,进而依次确定每组试验的液塑限。7组液限的均值与标准差分别为73.59%和13.41%,塑限的均值和标准差分别为39.3%和4.73%。这种离散性由试样的土质、物理状态与结构组分等因素所致。
4.渗透系数
渗透系数是表征土的渗透性的特性参数。结合土工试验教学,70余位学生共计完成27个渗透系数测试,试验所用材料为河北唐河定州段的天然河砂。采用6台常水头渗透仪在河北大学土工实验室完成,其圆筒内径为10 cm,高40 cm。图6给出测试成果,皆分布在0.04~0.12 cm/s范围内。测试结果的离散性由多种因素导致,比如,测试样本装样的密实度,试样级配情况、取样的偶然性、测试中的操作技术等。图6给出该测试数据的核概率密度曲线,可通过R中的density( )函数实现。这里选用的核函数为高斯核函数,带宽的计算方法为Silverman准则[14]。
5.压缩系数
侧限压缩系数是描述土的变形特性的主要指标之一。土在特定压力范围内的压缩系数,比如100 kPa和200 kPa压力下的多记为av。同樣结合土工试验教学,学生在近40余台压缩仪上完成72个压缩系数测试,试验所用材料为河北大学校园内的粉质粘土。压缩测试结果不确定性的主要原因包括:环刀样制备时土体的不均匀性、含水量和密实度差异等。图7给出测试结果,皆分布在0.2~0.7 MPa-1范围内,属于中高压缩性土。
图7采用箱线图对这些数据的统计特性进行展示。图中矩形盒中位数位置以粗实线示意,两端边的位置分别对应数据集的上下四分位数,异常值以圆圈标示。箱线图直观地给出异常值和数据集的偏态性。图7箱体向左右伸出的垂直部分表示数据的散布范围。异常值集中出现于较大值的一侧,中位数偏离上下四分位数的中心位置,则分布呈右偏态。该箱线图美中不足之处为:无法给出关于数据分布的偏态和重尾程度的精确度量。
6.剪切强度指标与容重
考虑参数不确定性对隧道围岩稳定性的影响,结合广西拉乌隧道围岩进行了较多的室内测试,最终工程师整理42个强度参数和容重参数值[15]。关于剪切强度参数,图8概念性地展示这些测试点的Mohr-Coulomb强度包络线变化。粘聚力的离散性可在纵(剪应力)轴上观察到,而内摩擦角的离散性可由各条线的斜率得到。在自然地质成因条件下,导致土体强度参数变异性的原因,文献[16]进行了详细地分析。

