数论函数方程φ(ab)=11φ2(a)+13φ2(b)的可解性*

郑芯芯， 刘 珍

(喀什大学 数学与统计学院,新疆 喀什 844008)

0 引 言

数论函数是一类重要的函数，研究数论函数方程的可解性是数论研究的一类重要课题.令数论函数φ(n)为Euler函数，对于包含Euler函数φ(n)的方程整数解的研究成果很多，如文献[1-8].令数论函数φe(n)为广义Euler函数，它是由蔡天新[9]教授等人所引入的一个函数.对于包含广义Euler函数φe(n)方程整数解的研究也有着不少的成果，如文献[10-11].而对于包含Euler函数φ(n)与广义Euler函数φe(n)方程整数解的研究成果甚少.在一些文献中，大多讨论的是单一的有关Euler函数φ(n)的线性与非线性方程的解，本文将讨论包含Euler函数φ(n)与广义Euler函数φ2(n)方程：

φ(ab)=11φ2(a)+13φ2(b)

(1)

的可解性问题，利用函数φ(n)与φ2(n)的有关性质，将给出该方程的一切正整数解.

1 引 理

引理2[12]对于正整数a与b，若b|a，则有φ(b)|φ(a)，其中符号“|”为整除符号.

引理4[12]当n≥3时，则φ(n)为偶数.

2 定理及其证明

定理1 方程(1)有整数解(a,b)=(79, 7)，(79, 9)，(79, 14)，(79, 18)，(158, 7)，(158, 9)，(13, 21)，(13, 28)，(13, 36)，(13, 42)，(21, 13)，(21, 26)，(26, 21)，(28, 13)，(36, 13)，(42, 13)，(14, 18)，(18,14)，(15,24)，(24, 15)，(12, 12).

证明情况1 当a，b中只有一数属于[1, 2]时，不妨设a=1, 2.当a=1时，有φ2(1)=0，由方程(1)可得φ(b)=13φ2(b)，此时方程无整数解；当a=2时，有φ2(2)=1，由方程(1)有

2φ(2b)=22 +13φ(b)

(2)

此时，有(2,b)=1,2.当(2,b)=1时，有2φ(b)=22 +13φ(b)无整数解.当(2,b)=2时，有4φ(b)=22 +13φ(b)，此方程无整数解.

情况2 当a，b都属于[1, 2]时，此时(a,b)=(1, 1)，(1, 2)，(2, 1)，(2, 2).经验证，以上(a,b)的值都不满足方程(1)，故此时无整数解.

情况3当a，b都属于[3, +∞)时，由方程(1)可得

2φ(ab)=11(a) +13φ(b)

(3)

设(a,b)=d，此时存在正整数a1与b1使得φ(a)=a1φ(d)，φ(b)=b1φ(d). 由式(3)可得

从而有2da1b1=11a1+13b1，则有(2da1-13)(2db1-11)=143，根据整数的分解可得到以下关系式:

当d=1时，a1=7，b1=77，则φ(a)=7，φ(b)=77，由引理4可得不符合条件.当d=7时，a1=1，b1=11，则φ(a)=6，φ(b)=66，有a=7, 9, 14 18，b=67, 134.由于以上a与b的值不满足(a,b)=7，因而此时方程(1)无整数解.

当d=1时，a1=78，b1=6，则φ(a)=78，φ(b)=6，因而a=79, 158，b=7, 9, 14, 18，此时方程(1)有整数解(a,b)=(79, 7)，(79, 9)，(79, 14)，(79, 18)，(158, 7)，(158, 9).

当d=2时，a1=39，b1=3，则φ(a)=39，φ(b)=3，此时φ(a)与φ(b)都为奇数，因而此时方程(1)无整数解.

当d=3时，a1=26，b1=2，则φ(a)=52，φ(b)=4，因而a=53, 106，b=5, 8, 10, 12.由于以上a与b的值不满足(a,b)=3，因而此时方程(1)无整数解.

当d=6时，a1=13，b1=1，则φ(a)=26，φ(b)=2.由于26为非Euler商数，故此时方程(1)无整数解.

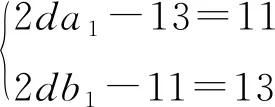
当d=1时，a1=b1=12，则φ(a)=φ(b) =12，因而a=b=13, 21, 26, 28, 36, 42，则方程(1)有整数解(a,b)=(13, 21)，(13, 28)，(13, 36)，(13, 42)，(21, 13)，(21, 26)，(26, 21)，(28, 13)，(36, 13)，(42, 13).

当d=2时，a1=b1=6，则φ(a)=φ(b) =6，因而a=b=7, 9, 14, 18，此时方程(1)有整数解(a,b)=(14, 18)，(18, 14).

当d=3时，a1=b1=4，则φ(a)=φ(b) =8，因而a=b=15, 16, 20, 24, 30，则方程(1)有整数解(a,b)=(15, 24)，(24, 15).

当d=4时，a1=b1=3，则φ(a)=φ(b) =6，因而a=b=7, 9, 14, 18.由于以上a与b的值不满足(a,b)=4，此时方程(1)无整数解.

当d=6时，a1=b1=2，则φ(a)=φ(b) =4，因而a=b=5, 8, 10, 12.由于以上a与b的值不满足(a,b)=6，此时方程(1)无整数解.

当d=12时，有a1=b1=1，则有φ(a)=φ(b) =4，因而a=b=5, 8, 10, 12，则方程(1)有整数解(a,b)=(12, 12).

综合以上讨论，可得本文结论.证毕.

3 结束语

对于形如φ(ab)=k1φ2(a)+k2φ2(b)的可解性问题，利用Euler函数φ(n)与广义Euler函数φ2(n)的有关性质，本文给出了当k1=11，k2=13时所对应的方程的一切正整数解，而对于k1与k2取其他整数时，利用本文所讨论的方式也可以得到解决.对于含单一的Euler函数φ(n)的形如φ(ab)=k1φ(a)+k2φ(b)的方程正整数解的讨论大体是通过枚举gcd(a,b)=d∈[1, max{2k1, 2k2}]来确定方程的解，而本文主要是通过整数的分解，利用因数或因式与整除来确定gcd(a,b)=d确定方程的解.

致谢：感谢张四保老师的悉心指导！