几类泛函微分方程的稳定性比较研究*
张纪强, 贾静丽
(1.安徽三联学院 基础部,合肥 230601; 2.安徽文达信息工程学院 计算机工程系,合肥 230032)
1 泛函微分方程含义
泛函微分方程,被称为时滞微分方程、微分差分方程,是对各种具有复杂变元的微分方程和带有各种滞后量的积分微分方程等的抽象和概况。相较于常微分方程,它对客观世界的描述更加精确和细致,在现代化的科学研究中具有重要的作用。
世界上第一个泛函微分方程是Condorcet[1]在1771年讨论Euler提出的古典几何学问题(是否存在一种曲线,经过平移和旋转运动后还能与渐缩线重合)时导出的。这个泛函微分方程为
自第一个泛函微分方程出现后,众多数学家[2-3]都对这类泛函微分方程进行过研究,但是鉴于其复杂性,并没有实质性的研究成果。随着广泛课题研究的出现,泛函微分方程获得了全面实质性的发展,并且在不断的发展中建立了几大方向。在现阶段研究中,一般有滞后型、中立型、超前型这几种。
20世纪50年代后,学者们[4-5]开始大量研究泛函微分方程的稳定性。在泛函微分方程中,稳定性是其中一项重要内容。
2 中立型泛函微分方程的稳定性
中立型泛函微分方程,可以简写为NFDE,它分为有界滞量的中立型泛函微分方程和无穷延滞的中立型泛函微分方程。
有界滞量的中立型泛函微分方程[6]可以表示为
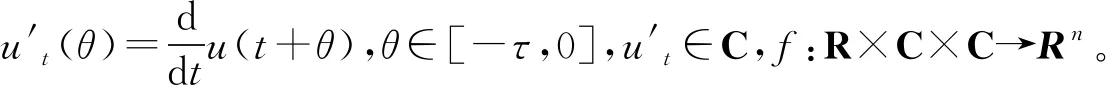
在对中立型泛函微分方程的稳定性研究方面,巴尔巴辛的V函数是基于n阶线性微分系统来构造的,对NFDE的稳定性研究是有效的。其他学者则采用类比法构建V函数对三到五阶非线性微分系统开展研究[7-9]。
如对于Lyapunov泛函微分方程来说,有稳定性、渐近稳定性和不稳定性3种情况。
令x′=f(x,t)中的平衡态为x0=0,如果存在正定函数V(x,t)有连续一阶偏导,且满足两个条件:
(1)V′(x,t)是非正定函数,那么该函数的平衡态具有一致稳定性;
(2) 如果Rn是正定函数V(x,t)的定义域Ω,对于∀t0和∀x(t0)≠0,当t>t0时,V′(x,t)不恒等于0,则该函数的平衡态具有一致渐进稳定性;

对于上述函数,如果满足下列条件:
①V′(x,t)是负定函数,那么该函数的平衡态具有一致渐进稳定性;
② 当x→∞时,V(x,t)→∞,则该函数的平衡态具有大范围一致渐进稳定性。
对于中立型泛函微分方程,无论是一阶还是二阶,甚至五阶都可以采用类比方法构建V函数求解方程的稳定性,这是常见且有效的方法。如Sun Y G[10]就证明了一个非线性多时滞的中立型泛函微分方程具有稳定性;武卉[11]也在基于Sun Y G的研究基础上证明了非自治非线性三阶中立型泛函微分方程的零解具有渐近稳定性特征。
中立型泛函微分方程本身包含很多种类,对于不同类别的NFDE还可以采用不同的方法进行研究。除了构建V函数以外,有的学者还采用了Lyapunov泛函和Razumikhin技巧、Lyapunov泛函和上鞅收敛定理、Runge-Kutta法、线性θ-法等对中立型的泛函微分的稳定性进行研究,并取得了较好成效。
3 非线性泛函微分方程的稳定性
Barwell[12]对线性模型方程的稳定性进行了研究,基于方程式(1)提出了P-稳定和GP-稳定,并验证了Euler法具有GP-稳定性。
(1)
Torelli[13]将原有的线性方程模型的稳定性研究拓展到非线性刚延迟微分方程处置问题中,基于方程式(2)提出了GRN-和RN-稳定性,同时验证了向后的Euler法具有GRN-稳定。
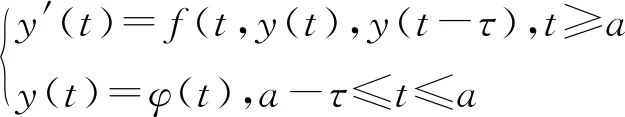
(2)
这里f满足下面条件:
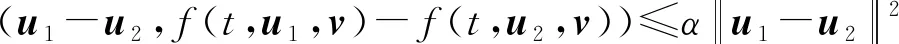
Torelli的研究与后来的学者研究发现要实现RN-稳定非常困难,其条件非常苛刻。
李寿佛[14]在有限维欧式空间中探讨了一般形式的非线性刚性Volterra泛微分方程的初值问题,构建了B-稳定的新理论,从而为非线性刚性的常微分、延迟微分和积分微分方程等奠定了统一的数值方法稳定性的理论基础,然而对于中立型泛函微分方程,B-理论并不适用。

(3)
其中,a,b,τ为常数,取值范围为-∞ 针对条件: 以及 通过求解方程式(3),采用一般线性法和Runge-Kutta法建立了B-稳定,新B理论的建立为非线性刚体积分微分方程的稳定性研究提供了统一的理论基础。 以上的研究都是以单边Lipschitz和内积范数为条件的,都是探讨有限维内空间中的初值问题。然而,现实科学工程中许多问题都是刚性问题,这导致使用内积范数时,最小单边的Lipschitz常数往往会取巨大的正值,这在一定程度上影响了其使用,对此,李寿佛[14]还进一步对Banach空间X中的一类Volterra泛函微分方程类D(α,β,μ1,μ2)进行了研究,并验证了渐进稳定结果和理论解的稳定性。 (4) 方程式(4)还需要满足以下条件: 文立平[15]进一步研究了Dλ*(α,β,μ1,μ2)和Dλ*,δ(α,β,μ1,μ2),并提出了θ-法、对角隐式和显式Runge-Kutta、线性多步法等的稳定性。 Banach空间是具有范数并对范数完备的一个向量空间,它是由波兰的斯特凡·巴拿赫等人于1920—1922年期间提出来的,并以他的名字来命名。随着计算机的快速发展,对泛函微分方程的研究有了突破性的进展,特别是对Banach空间中的泛函微分方程的研究。当前,许多关于无限维泛函微分方程的研究都是在Banach空间下进行的。在Banach空间下,非线性泛函微分方程通常可以用θ-法、对角隐式和显式Runge-Kutta、一般线性多步法等方法进行稳定性分析。 随着信息技术的快速发展,许多领域的工程系统都存在时滞现象,系统的状态往往受到之前的时间影响,即某个时间的状态会对该时间点后的状态产生影响。由此,存在随机时滞微分方程: dx(t)=f(x(t),x(t-τ))dt+ g(x(t),x(t-τ))dW(t),t≥0 (5) 当函数依赖系统滞后项时,产生中立型随机时滞微分方程: d[x(t)-G(x(t-τ))]=f(x(t),x(t-τ)(dt+ (6) 其中,中立项为G(x(t-τ)),G(0)=0。 1982年,Nosov he和Kolmanovskii[16]进一步拓展更广泛的中立型随机泛函微分方程,可以表示为 d[x(t)-G(xt)]=f(x(t),xt)dt+ (7) 其中xt=x(t+θ),-τ≤θ≤0。 在中立型随机泛函微分方程的稳定性研究方面,Mao[17-18]利用Razumukhin技术验证了中立型随机泛函微分方程的均方指数稳定性;Liao[19]也验证了中立型随机时滞微分方程的理论解具有指数稳定性特征;Luo等[20]指出局部Lipschitz条件,验证了方程理论解具有指数均方稳定性特征。 Huang[21]验证了随机时滞微分方程(式(5))的分步θ-法和θ-法均具有稳定性。 fT(t,u,v)Qf(t,u,v)≤K1uTQu+K2vTQv (t,u,v)∈R+×Rd×Rd 其中,K1,K2为常数,Q是正定矩阵,对于有界步长,θ-法具有均方渐近稳定性,分步θ-法具有均方指数稳定性。 Liu[22]验证了式(6)即中立型随机时滞微分方程的分步θ-法和θ-法具有稳定性。方程式(6)中,令 fT(t,u,v)Qf(t,u,v)≤K1uTQu+K2vTQv (t,u,v)∈R+×Rd×Rd 对于任意的步长来说,分步θ-法具有均方指数稳定性。对于有界步长,θ-法都具有均方渐近稳定性。 Zhou[23]利用非负半鞅收敛定理对方程式(7)进行了研究,当BEM符合单边的Lipschitz条件,BEM法具有几乎必然指数稳定性。事实上,式(7)是很难得出其解析解的,因此Zhou等[24]的数值方法的稳定性研究是非常必要的。许多学者对式(7)开展不同数值方法的稳定性研究,如Zong等[24]对BHM法和EM法的几乎必然指数稳定和矩指数稳定性进行了探讨;Yu[25]探讨了的BEM和EM法的指数稳定性和几乎必然渐近稳定性;Wang[26]探讨了BEM法的均方渐近稳定性。 泛函微分方程的种类有很多,其数值方法的稳定性研究是泛函微分方程的研究重点。本文只选取了中立型泛函微分方程、非线性泛函微分方程和随机时滞泛函微分方程的稳定性进行了概括性综述。不同类型的泛函微分方程采用的数值方法有相似的方法,但也有一些区别。如中立型泛函微分方程可以Lyapunov泛函和Razumikhin技巧、Lyapunov泛函和上鞅收敛定理、Runge-Kutta法进行稳定性研究。对于非线性泛函微分方程可以采用θ-法、对角隐式和显式Runge-Kutta法、一般线性多步法等进行研究。对于随机时滞泛函微分方程则可以采用θ-法、Euler-Maruyama法、θ-分步法、Backward Euler-Maruyama法等进行稳定性分析。无论哪种方法,都旨在为泛函微分方程的稳定性研究提供可靠的理论保障。


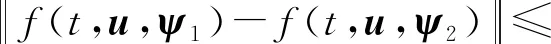
4 随机时滞泛函微分方程的稳定性

g(x(t),x(t-τ))dW(t),t≥0
g(x(t),xt)dW(t),t≥0


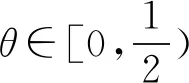
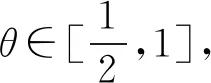
5 结束语

