基于IOWC-GOWA算子及相对熵的区间型组合预测模型*

杜 康， 袁宏俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

0 引 言

由于预测对象的模糊性和复杂性，单项预测方法的预测结果与实际情况可能会产生较大的偏差。为此，Bates J M和Grange C W J[1]在1969年首次提出组合预测方法，即将几种单项预测方法进行组合。由于组合预测方法在实际预测过程中的精度优于单项预测方法，因此一些国内外学者对其进行了研究，并取得了一定的研究成果[2-7]。在实际预测过程中，预测对象有时候并不能以一个确定的实数给出，因此区间型数据组合预测的研究受到学者们的重视。现有文献对于区间型组合预测模型的研究主要可以分为以下几类：

(1) 将区间数通过连续区间的信息集成算子转化为普通的实数。文献[8]提出了IOWC-GOWA算子，利用该算子将区间数集结成实数，并用指数支撑度作为最优准则构建组合预测模型；文献[9]提出了IOWC-GOWHA算子，将区间数转化为实数，利用灰色趋势关联度作为相关性指标构建了基于IOWC-GOWHA算子的组合预测模型；文献[10]在C-OWHA算子和IGOWLA算子的基础上，提出了IGOWLC-OWHA算子，将区间数集结为实数，用Theil不等系数作为最优准则构建组合预测模型；文献[11]提出了COWG-WPA算子，将区间数转化为实数，用广义绝对误差λ次和作为准则构建组合预测模型。

(2) 利用区间数自身的信息，即区间数的中点和半径或者是区间数的左、右端点等信息。文献[12]一方面利用区间数的中点和半径，并以区间中点和长度的最小绝对误差准则，构建了多目标规划问题，引入偏好系数将其转化为单目标规划问题的组合预测模型，另一方面利用区间数的左、右端点，分别以向量夹角余弦和Theil左右不等系数为准则构建多目标规划问题，同样引入偏好系数将其转化为单目标规划问题的组合预测模型；文献[13]和文献[14]分别利用区间数的中点、半径和左、右端点，以最小误差平方和作为准则，构建多目标规划问题，并引入偏好系数将其转化为单目标规划问题的组合预测模型。

(3) 将区间数转化为联系数。文献[15]将区间数转化为二元联系数，并以联系数贴进度作为最优准则构建组合预测模型；文献[16]也是将区间数转化为二元联系数的形式，以向量夹角余弦作为相关性指标构建组合预测模型。本文采用第一种思路，先利用IOWC-GOWA算子将区间型数据转化为实数，并对集结后的实数进行标准化处理，引入相对熵作为最优准则来构建区间型组合预测模型，并通过实例验证模型的合理性和有效性。

1 基本概念

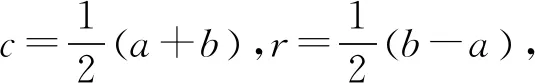
定义2[17]设[a,b]为区间数，称

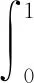
FQ([a,b])=(1-μ)a+μb

定义3[18]设fw:Rn→R，λ≠0，若

定义4[19]设[a,b]为区间数，λ≠0，称

为连续区间的广义有序加权平均(C-GOWA)算子。其中，Q(y)为BUM函数。根据定义2，同理可得：

定义6[8]设诱导二维区间数组V={〈v1,[a1,b1]〉,〈v2,[a2,b2]〉,…,〈vn,[an,bn]〉}，fw:Ω+→R+，λ≠0，称

fw(〈v1,[a1,b1]〉,〈v2,[a2,b2]〉,…,〈vn,[an,bn]〉)=

定义7[21]设xi,yi>0，且xi,yi∈(0,1)，则称

为序列X相对于序列Y的相对熵，其中，X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)，i=1,2,…,n。

定理1[21]如果函数h(x,y)为序列X相对于序列Y的相对熵，则

(1)h(x,y)≥0；

(2) 当且仅当xi=yi，i=1,2,…,n，有h(x,y)=0。

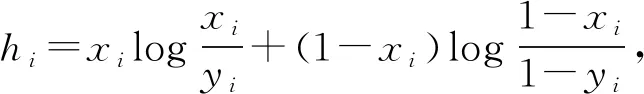
log[yi+(1-yi)]=

log 1=0

由hi≥0，得h(x,y)≥0，原命题得证。

(Jensen不等式)

所以h(x,y)=0时当且仅当xi=yi，i=1,2,…,n。

由定理1可知，当序列X=(x1,x2,…,xn)相对于序列Y=(y1,y2,…,yn)的相对熵最小且为0时，序列X和序列Y完全相同，即相对熵越小表示序列X和序列Y之间的符合程度越大。因此相对熵可以刻画两个标准化的序列之间的差异程度，所以可以基于相对熵达到最小的思想构建区间型组合预测模型。

2 模型构建

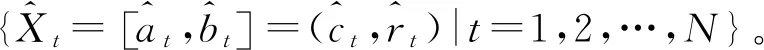
定义8

则称vit为第i种单项预测方法在第t时刻的预测精度。其中，vit∈[0,1]，i=1,2,…,m，t=1,2,…,N。

定义9 利用预测精度vit作为诱导值，可以构造出第t时刻的诱导二维区间数组V={〈v1t,[a1t,b1t]〉,〈v2t,[a2t,b2t]〉,…,〈vmt,[amt,bmt]〉}，令

Yt=GQ([at,bt])=

定义10 设Yt,Yit>0，且Yt,Yit∈(0,1)，令

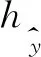
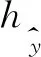
(1)

上述模型式(1)的权系数W=(w1,w2,…,wm)可以通过Lingo或者Matlab软件进行求解。

定理2 设hmin=minhYit,hmax=maxhYit，i=1,2,…,m，若

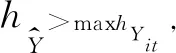
3 实例分析

为了验证组合预测模型式(I)(即基于IOWC-GOWA算子及相对熵的区间型组合预测模型)的有效性，现分别用平均区间位置误差平方和(fMSEP)、平均区间长度误差平方和(fMSEL)、平均区间误差平方和(fMSEI)以及平均区间相对误差和(fMRIE)作为评价指标，其中：

fMSEI=fMSEP+fMSEL=

显然，上述4种误差指标越小，表示该区间型组合预测模型的有效性相对越高，即预测精度相对越高。fMSEP和fMSEL越小，分别表示预测区间和实际区间的中点和半径的误差越小。而fMSEI集合了区间的中点和半径的误差信息，所以更能作为衡量模型有效性的指标。对于fMRIE来说，若fMRIE>1，则说明预测区间和实际区间分离，即没有重合部分，若0≤fMRIE≤1，则说明预测区间和实际区间部分重合，并且fMRIE越小，说明重合比例越大，即模型有效性越高。本文利用文献[22]中的数据来进行实例分析，各数据见表1。

根据定义8可以计算出3种单项预测方法在各个时刻的预测精度，结果见表2。

表 1 实际区间数和3种单项预测区间数

表 2 3种单项预测方法在各个时刻的预测精度

根据定义9，可以计算出每个时刻基于IOWC-GOWA算子的组合预测值，以t=1和t=2为例：

表 3 实际集结数序列Yt和3种单项预测集结数序列Yit

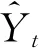
根据标准化处理后的数据，可以用Lingo软件对组合预测模型式(1)的最优加权向量W=(w1,w2,w3)进行求解，结果见表5。

根据表5中的各单项预测的最优加权向量W=(w1,w2,w3)以及经过每个时期预测精度诱导过后的各单项预测的区间数，可以计算出不同λ取值下每个时期的组合预测区间数，结果见表6。

表 4 实际集结数和3种单项预测集结数的标准化序列

表 5 不同λ取值下的最优加权向量W=(w1,w2,w3)

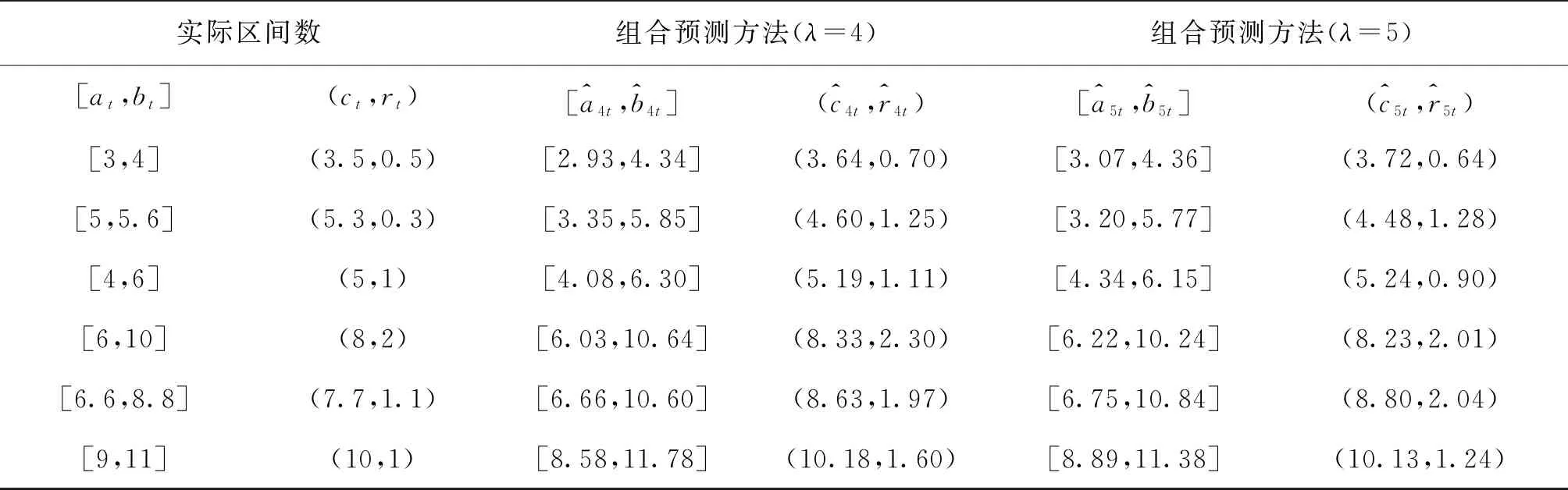
表 6 实际区间数以及不同λ取值下的组合预测区间数

为了验证组合预测模型式(1)的有效性，分别从相对熵和4种误差指标MSEP，MSEL，MSEI以及MRIE的角度来分析。根据表4中的数据，可以计算出不同λ取值下3种单项预测方法的相对熵，运用Lingo软件可以得到组合预测模型式(1)的最优相对熵，结果见表7。根据4种误差指标的公式，可以分别计算出3种单项预测方法以及不同λ取值下的组合预测方法的MSEP，MSEL，MSEI以及MRIE，结果见表8。

表 7 不同λ取值下各种预测方法的相对熵

表 8 各种预测方法的误差指标

从表7和表8中可以看出：从相对熵的角度来看，λ=4时，组合预测方法的相对熵小于3种单项预测方法的相对熵；λ=5时，组合预测方法的相对熵也远小于单项预测方法1和2的相对熵，和单项预测方法3的相对熵十分接近。从4种误差指标的角度来看，组合预测方法的MSEP，MSEI以及MRIE均小于3种单项预测方法，虽然组合预测方法的MSEL大于单项预测方法2，但小于单项预测方法1和3，至少说明组合预测模型式(1)是非劣的。由以上结果可以看出，组合预测模型式(1)可以有效提高区间型数据的预测精度。

4 结束语

本文从信息论的角度出发，提出构建区间型组合预测方法的新思路。先利用IOWC-GOWA算子将区间数进行集结，转化为普通实数，并对其进行标准化处理。引入相对熵作为最优准则，构建了基于IOWC-GOWA算子及相对熵的区间型组合预测模型，并用文献[18]中数据以及4种误差指标对其有效性进行了验证，结果显示，该组合预测模型能有效提高预测精度。但是，由于本文采用的是IOWC-GOWA算子，所以参数λ以及BUM函数的选取都会对模型的有效性产生影响。另外，对于集结数序列的标准化处理方式也可能会对模型的结果产生一定的影响，今后将对这些因素作进一步研究，以完善本文方法。