分数阶灰色累加生成算子性质研究*
孟 伟
(1.电子科技大学 经济与管理学院, 成都 611731; 2.重庆工商大学 商务策划学院, 重庆 400067)
0 引 言
中国学者邓聚龙教授在20世纪80年代创立了灰色系统理论,该理论与模糊数学、粗糙集理论、未确知数学均是不确定性系统的代表性理论[1-2]。灰色累加生成算子是使灰色过程原始数据序列由无规律变为近似指数规律的一种方法,即由灰变白,在灰色系统理论中占有非常重要的地位[2]。灰色预测模型GM(1,1)通过对原始数据序列进行一阶累加生成弱化数据的随机性,得到符合近似指数规律的数据序列,然后进行建模,再累减还原为原始数据序列的预测值,它在社会经济领域得到了广泛应用。围绕灰色累加生成,研究人员在灰色累加生成算子拓展与性质等方面做了大量研究工作,形成一系列新算子与新模型,有效扩大了灰色预测模型的应用范围。戴文战[3]推导出n次累加生成算子的二项式表达式;宋中民[4]给出一次反向累加生成算子定义并建立了灰色GOM(1, 1)模型;Liu Y R等[5]利用泰勒展开式在分数阶差分算子基础上给出了分数阶累加算子的近似表达式;毛树华等[7]利用二项式系数定义了分数阶累积算子的表达式;吴利丰等[8-10]证明了分数(0 定义1[2]设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始数据序列,D为算子运算符, X(0)D=(x(0)(1)d,x(0)(2)d,…,x(0)(n)d)其中: 则称D为X(0)的一阶累加生成算子,记为1-AGO。 定义3[2]称r阶算子Dr为X(0)的r阶累加生成算子,r∈Z+,记为r-AGO。 记X(r)=(x(r)(1),x(r)(2),…,x(r)(n))为x(0)的r阶累加生成序列,其中: k=1,2,…,n 定义4[2]设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,X(1)=(x(1)(1),x(1)(2),…,x(1)(n))为X(0)的一阶累加生成算子,其中 则有 X(1)=(x(0)(1),x(0)(1)+x(0)(2),…, 根据累加生成算子定义有 定理1 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,X(2)=(x(2)(1),x(2)(2),…,x(2)(n))为的二阶累加生成算子,其中 证明可用数学归纳法严格证明: x(2)(s+1)=x(2)(s)+x(1)(s+1)= 也成立。 定理2 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,r∈Z+,X(r)=(x(r)(1),x(r)(2),…,x(r)(n))为X(0)的r整数阶累加生成算子,其中: (1) x(r)(k)展开式中x(0)(i)的系数为 (2) 证明可用数学归纳法严格证明: 当r=1时,x(1)(k)= 若X(s)=(x(s)(1),x(s)(2),…,x(s)(n))为x(0)的s阶累加生成算子,若 x(s)(k)= 成立,则 X(s+1)(k)=(x(s+1)(k-1)+x(s)(k))= 也成立,证毕。 定义5n∈R且n∉{0,-1,-2,-3,…},Γ(n)为Gamma函数,定义为 利用分部积分法,Gamma函数具有递归关系 Γ(n+1)=nΓ(n) 当n∈N时,有 即Gamma函数是阶乘的推广。 由于式(2)中x(r)(k)展开式中x(0)(i)的系数 式(1)可写为 k=1,2,…,n x(r)(k)展开式中x(0)(i)的系数为 定义6 设r=R+,X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,X(r)=(x(r)(1),x(r)(2),…,x(r)(n))为X(0)的r阶累加生成算子,其中 k=1,2,…,n 特别当r=1时, 即为一阶累加生成算子。 定义7 设X(m)=(x(m)(1),x(m)(2),…,x(m)(n))为原始序列,X(l)=(x(l)(1),x(l)(2),…,x(l)(n))为变换序列,r=l-m。 若l-m>0,X(l)是X(m)是r阶累加生成序列,X(l)=X(m)Dl-m。 定义8 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,X(r)=(x(r)(1),x(r)(2),…,x(r)(n))如定义6所示, x(r)(k)= 是r阶灰色累加生成算子的矩阵表达式。 命题1 分数阶灰色累加生成算子满足不动点定理。 证明分数阶灰色累加生成算子的解析表达式为 当k=1时, 即x(0)(1)是x(r)(k)的不动点,证毕。 命题2 当r∈(0,1)时,r阶累加生成算子满足新信息优先原理。 证明x(r)(k)表达式中,x(0)(i)系数为 x(0)(i-1)系数为 新信息优先是灰色预测模型利用信息的一条重要原理。 命题3 当r>1时,r阶累加生成算子中的旧信息具有更大的权重。 证明根据式(2)有 命题4 当r=1时,一阶累加生成算子中信息均等。 证明当r=1时,有ai-1=ai,表示x(r)(k)表达式中,x(0)(i-1)与x(0)(i)具有相同的权重系数1,即满足信息均等原则,证毕。 定理3 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,X(r)=(x(r)(1),x(r)(2),…,x(r)(n)),r∈R+,为X(0)的r阶累加生成算子,其中 x(r)(k)= k=1,2,…,n x(r)(k)展开式中x(0)(i)的系数为 (3) 证明因为 Γ(n+1)=nΓ(n)Γ(r+k-i)= (r+k-i-1)Γ(r+k-i-1)= (r+k-i-1)(r+k-i-2)Γ(r+k-i-2)= (r+k-i-1)(r+k-i-2)(r+k-i-3)Γ(r+k-i-3)=…= (r+k-i-1)(r+k-i-2)(r+k-i-3)… (r+3)(r+2)(r+1)rΓ(r) 因此, x(r)(k)= 定理4 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,X(0)是X(0)的r阶累加生成序列,其中: k=1,2,…,n 证明可用数学归纳法严格证明: k=1时, k=2时, 证毕。 推论1 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,r∈Z+,X(r)是X(0)的r阶累加生成序列,X(r)(k+1)和X(r)(k)关于各项系数之和有如下关系: 证明由式(2)可知 证毕。 定理5 设p∈R+,q∈R+,X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始序列,若X(p)是X(0)的p阶累加生成序列,X(q)是X(0)的q阶累加序列,则X(p+q)是的p+q阶累加序列,(X(p))(q)是X(p)的q阶累加序列,(X(q))(p)是X(q)的p阶累加序列,分数阶累加生成算子满足交换律和指数律,即 (X(p))(q)=(X(q))(p)=X(p+q) 证明先证(X(p))(q)=X(p+q)。 可用数学归纳法严格证明 k=1时, 成立。 k=2时, (p+q)x(0)(1)+x(0)(2) (x(p)(2))q= qx(0)(1)+px(0)(1)+x(0)(2)= (p+q)x(0)(1)+x(0)(2)=x(p+q)(2) 成立。若 成立,则 (x(p)(s+1))q= x(p+q)(s+1) 也成立。 则(X(p))(q)=X(p+q)成立。 同理可证(X(q))(p)=X(p+q)成立。 则(X(p))(q)=(X(q))(p)=X(p+q)结论成立。 证毕。 2013—2017年,中国国内生成总值数据序列为X0=X(0)=(59.524 4,64.397 4,68.905 2,74.358 5,82.712 2)(单位:万亿元),经计算可得: X1=X(1/4)=(59.524,79.279,94.305,108.62,125.28) X2=X(1/3)=(59.524,84.239,103.6,121.93,142.51) X3=X(1/2)=(59.524,94.16,123.43,151.56,182.13) X4=X(2/3)=(59.524,104.08,144.91,185.47,229.31) X5=X(3/4)=(59.524,109.04,156.27,204.11,256.01) X6=X(1)=(59.524,123.92,192.83,267.19,349.9) (X(1/4))(3/4)=(X(3/4))(1/4)=(X(1/3))(2/3)= (X(2/3))(1/3)=(X(1/2))(1/2)=X(1) 原始数据序列与分数阶累加生成序列曲线图见图1所示。由计算结果可直观验证,分数阶累加生成序列满足不动点定理、交换律与指数律,且分数阶累加算子的阶数值r越大,累加数据序列增长幅度越大。 图1 不同阶数取值的分数阶累加生成序列Fig.1 Accumulating generation sequences of different values of order 给出了灰色累加生成算子从一阶拓展到整数阶和分数阶的详细推导步骤,并从理论上证明了分数阶灰色累加生成算子满足不动点定理、信息优先原理、交换律和指数律等定理。通过分数阶灰色累加生成算子,可精确调节原始数据序列的累加生成阶数,使得分数阶累加生成序列更符合指数规律,从而提高灰色预测模型的建模精度与适用范围。1 定义及定理

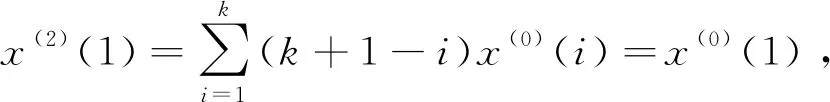











2 分数阶灰色累加生成算子性质
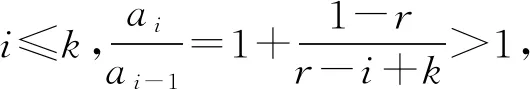


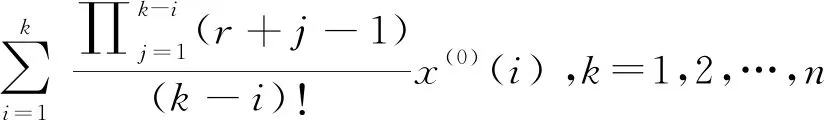

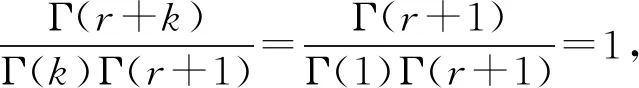


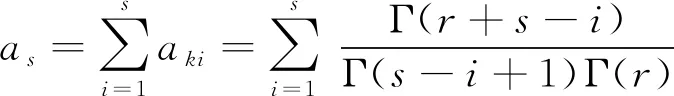







3 算例与数值验证

4 结 论

