DPS系统的动力学分析与控制*

何宏骏，崔 岩，孙 观

(上海工程技术大学 机械与汽车工程学院,上海 201620)

0 引 言

随着对非线性动力学现象的深入研究，系统的稳定性问题成为动力系统中的一个较为重要的方向，其中时滞是指系统在过去某个时间上的状态对于当前状态的影响，主要表现为延迟作用，如通信线路中常常会遇到信号堵塞,经济学中的察觉时滞,交通运输中的传递拥堵,蒸气和流体在管道中的流动时滞,电信号在长线上的传递时滞等，均表现为时间延迟。对于系统中的时滞现象并不能直接研究与控制,必须建立相应的数学模型,从而研究其带有时滞项的微分方程。自从1963年Lorenz[1]建立数学模型并提出第一个混沌系统以来,专家学者们随后也相继提出许多混沌系统如 Chen 系统[2]、Lü系统[3]、Liu系统[4]、Qi系统[5]、Chua系统[6]等。

对于自然界以及实际生产中的非线性系统[7-8]，专家学者们研究了其产生原因及控制方式[9]。文献[10]根据Lorenz系统的特性,设计了一个针对彩色图像的加密算法,通过在电子网站中的运用,获得良好的效果；文献[11]针对机械系统故障信号弱的问题,提出了一种新的关于Lorenz系统的故障检测法,并通过转子冲击实验，验证了该方法的有效性；文献[12]通过研究超混沌Chen系统,提出了具有双重加密效果的分数阶超混沌Chen系统的视频加密通信方法；文献[13]通过简化的Lorenz系统，并通过引入切换控制函数得到网格多涡卷混沌吸引子，设计电路验证了该系统的通讯保密性能；文献[14]提出一种基于Chen系统的新加密算法,具有较强的抗干扰能力；文献[15]研究了分数阶Chen系统的动力学特性，利用多种混合电路实现了该分数阶系统；文献[16]通过建立系统的动力学模型，利用数值积分法求解系统的非线性振动响应,分析裂纹角和裂纹深度对系统运动状态的影响；文献[17]通过分析平衡点的稳定性给出了单时滞类Lorenz系统的Hopf分岔条件。

本文将Chen系统的第一个非线性方向改为

从而得到一个新的时滞扰动类Chen系统。以一类新的时滞扰动Chen系统为分析对象,结合规范型定理和Hopf分岔定理,分析该系统的平衡点的稳定性并给出Hopf分岔的发生条件，通过多组仿真实验验证了理论分析的正确性。在对该时滞系统的控制方面采取了线性状态控制器的反馈控制，增强了控制器的作用范围，同时得出了时滞系统反馈系数的选择范围，实现了对该时滞系统的有效控制。

1 新系统的动力学分析

混沌系统的动力学方程形式如下：

(1)

其中[x，y，z]T∈R表示系统的状态变量，a，b，c为系统参数。该系统由2个非线性项和4个线形项组成。此系统吸引子图像与洛伦兹系统相似，但在拓扑上并不等同于洛伦兹系统和其他类似洛伦兹的系统。

1.1 对称性

将系统式(1)中x和y坐标做变换(x,y,z)→(-x,-y,z),系统保持不变，则系统式(1)关于z轴中心对称。对称性会对系统产生很多方面的影响，如周期解、分岔、相图在平面上的投影等。

1.2 耗散性分析

对于系统式(1)有如下等式(2)：

(2)

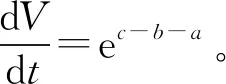
1.3 平衡点及分岔分析

从而系统式(1)在平衡点O(0,0,0)的特征方程为λ3+(a+b-c)λ2-(ab-ac-bc)λ-abc=0,其中a1=a+b-c,a2=ab-ac-bc,a3=abc,根据Routh-Hurwitz判据，当a1>0,a1a2-a3>0，a3>0时系统式(1)的平衡点O(0,0,0)是渐进稳定的。由于系统式(1)的平衡点总是可以通过坐标平移变换到零平衡点，故P+和P-的稳定性可以类似考虑。

由文献[16]可知，对于两个平衡点P+和P-，有以下3种情况：当a>c> 0和b> 0，那么P+是稳定的;当c≥a> 0，那么P+是不稳定的;如果ac≠0且b=bH，则系统式(1)具有Hopf分岔。

1.4 数值模拟

系统式(1)选取参数a=35,b=3,c=25，迭代初始点选(8,1,1),默认步长，积分上限为50，系统的吸引子图像如图1所示。从图1可以看出，当a=35,b=3,c=25时，系统式(1)呈稳定的混沌运动，起点(8,1,1)并不在吸引子中，故迭代过程产生了一条吸引子外的轨线，因为耗散作用是一种稳定的作用，最终将任意起点的迭代过程发生的轨线都收缩到吸引子中去，达到稳定状态。由文献[16]可知系统式(1)的3个李雅普诺夫指数分别为λL1=2.754 5,λL2=0.016 5,λL3=-15.771 2，其中λL2近似等于0，则系统式(1)只有一个正李雅普诺夫指数，该状态下的吸引子是奇异吸引子，即其维数是分数维的。

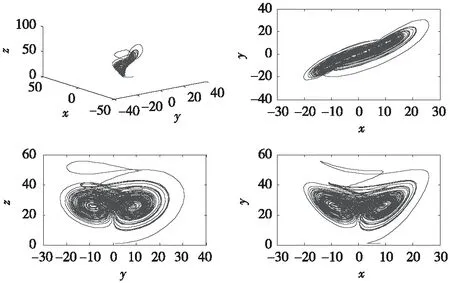
图1 系统式(1)的相图Fig.1 System (1) phase diagram

2 混沌控制

2.1 微分反馈控制

本节将运用黄报星提出的微分反馈控制法[17]对系统式(1)进行稳定控制,所谓微分反馈控制就是当系统接近目标周期态的时候，利用现态与目标态的差值作为被控系统的输入，驱动系统达到周期态，并使之稳定的一种控制方法。现对系统式(1)进行控制，受控系统如下：

(3)

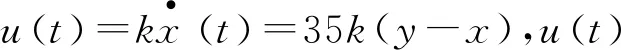
所对应的特征方程为λ3+(13-35k)λ2+(180-105k)λ+5 250=0，特征方程对应的系数为a1=13-35k，a2=180-105k，a3=5 250，根据Routh-Hurwitz定理可知当a1>0，a2>0，a1a2-a3>0时系统稳定到平衡点P+点，求得k的取值范围为k∈(-∞,-0.33)。由于系统具有对称性，故P-点的稳定性与P+点的稳定性一样，因此当k在此范围内，系统式(3)的解渐渐趋近于P+点和P-点。受控系统取初值(-4，-4，10),k取-1时系统稳定与平衡点如图2、图3所示。

图2 系统式(3)的相图Fig.2 Controlled system (3) phase diagram

(a)

(b)

(c)

2.2 x|x|控制

x|x|控制法属于外力反馈控制法，其特点是当无扰动的系统存在混沌时，从外部给系统输入一个强迫信号，用以与系统的输出量进行比较，并给出控制信号作为对系统的一种微扰。当然，无微扰时的系统必须存在混沌吸引子，只有这样才有可控制的无穷多的周期轨道或非周期轨道。考虑如下定义的n维非线性混沌系统[10]：

(4)

U=Ky|y|

(5)

式(5)中K为反馈增益矩阵。将该非线性反馈控制器负反馈加到系统式(1)中，则受控系统为

(6)

这样形成的非线性控制器简单且只需要稍微改变参数，相对小的反馈增益，就能够将混沌运动控制到各种规则的运动。结合式(6)，在系统式(1)的第一个方程中加入负反馈变量，就可以得到受控的系统方程为

(7)

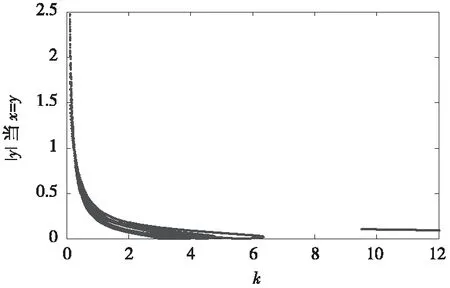
基于以上系统式(7)，通过matlab数值仿真，得到了关于控制参数k的全局分岔图(图4)：

从图4可以观测到，当k=0.9时，系统出现倍周期分岔，由稳定的2p轨道进入1p轨道，在k=1.1时又从1p轨道进入混沌状态，在k=1.5时由混沌状态转为稳定的2p轨道，k=1.6时又从2p轨道转为1p轨道。在后面的过程中随着控制参数k的不断增大，系统先处于混沌状态发生分岔，而后又进入周期状态，而后又分岔进入混沌状态，如此交替进行。第一次从混沌进入周期再进入混沌的参数k间距0.5，第二次参数k的间距是0.65，第三次的间距为0.8，可见每以此窗口期的时间在增加，且每次增加约0.15。当k取在窗口期的时候，系统是周期的，x的迭代值是震荡的。

图4 参数k的局部分岔图Fig.4 Local bifurcation diagram of parameter k

2.3 y|y|控制

从最早2003年闵富红、徐振源正式提出x|x|控制[13]以后，许多学者对其他系统也运用了该方法进行控制，但是其负反馈控制项都是加在第一个方程中，反馈量也只是x。而对于x|x|控制的效果而言，只能使系统产生周期性的窗口期，并不能完全消除混沌。本文发现的y|y|控制项能直接消除系统的混沌，且达到稳定的速度很快。在本节中将输出y作为非线性负反馈控制器加到系统式(1)的第二个方程中去，可得如下受控系统为

(8)

下面给出4个经典系统的受控分岔图。图6(a)为Chen系统受控后的分岔图，Chen系统在控制参数k>1以后就进入周期态，混沌现象被消除，不经过倍周期分岔。图6(b)为Rossler系统受控后的分岔图，当参数k=9时，系统开始进入周期态，在k∈(6.2,9)时，系统分岔图为空白，具体原因有待考察。

(a) Chen系统

(b) Rossler系统

(c) Lü系统

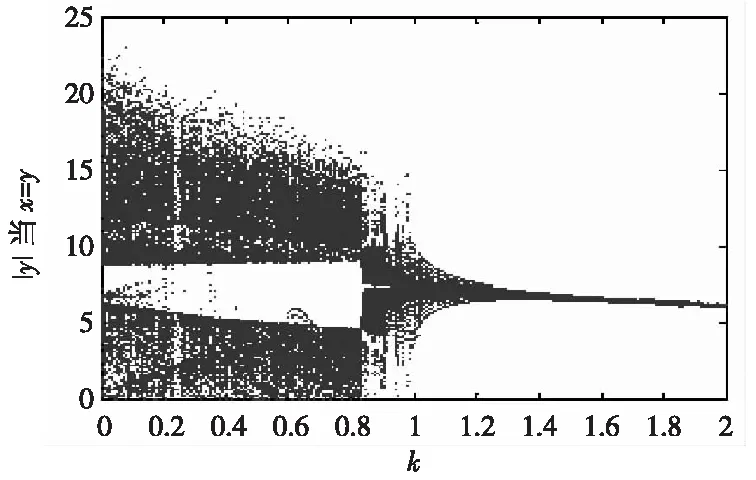
(d) Lorenz系统

图6(c)为Lü系统受控后分岔图，Lü系统在参数k=0.26时开始脱离混沌状态，直到k=0.35左右才完全进入周期态，也没有经过倍周期分岔直接进入稳定态。图6(d)是Lorenz系统的受控后分岔图，可以看出它与Lü系统有相似之处，没有经过倍周期分岔直接脱离混沌状态转而进入稳定态,而且稳定性较好。

2.4 恒定外激励控制

人们研究混沌控制的最终目的就是要把混沌现象为其所用或者消除不必要的混沌现象，恒定外激励控制就是消除混沌的一种方法，这种方法的核心要点就是选取合适的恒定外激励控制项u(t)=k，并把该控制项加到系统式(1)的第二个方程上，可得如下受控系统:

(9)

得到受控系统后，通过选取不同的控制项参数k的值，可将原本混沌的系统控制稳定到周期轨道上，以达到消除混沌的目的。图7给出了系统(9)关于参数k的分岔图，当控制参数k=24时，系统出现窗口期，随后在k=25时又进入混沌状态，当k=28时系统由混沌状态转入倍周期分岔，当k=29.5时，系统由稳定的4p轨道转入稳定的2p轨道，随后一直稳定，混沌现象被消除。这种添加一个常数的方法不但能使系统产生窗口期，同时还能发生亚临界倍周期分岔，使系统具有丰富的动力学现象，为以后对该系统进行分岔研究的学者提供一个方向。本文所给图像是将恒外激励控制项加在第二个方程中，将控制项添加到第一个或者第三个方程中，均可以实现混沌消除的功能，为后续研究混沌消除的学者提供了一条思路。

图7 受控系统(9)部分分岔图Fig.7 System (9) partial bifurcation diagram

3 结 论

本文对新提出的混沌系统进行了动力学分析与混沌控制研究。分析了混沌系统的动态特性，通过相图、分岔图和李雅普诺夫指数的数值模拟，验证了混沌系统的动力学现象。然后运用微分反馈控制、x控制、恒励磁控制方法,分别将系统向稳定点和周期轨道上控制，并通过在方程第二项中添加y控制项，使混沌现象消除。数值模拟证明该方法能有效地消除混沌。通过对新系统的控制，为混沌通信序列提供了一种新的混沌形式，提高了混沌的跟踪速度。