渐薄工艺对反曲弓能量转化效率的影响

梁 森， 朱弈嶂， 张德春， 李 鹏

(西南交通大学 力学与工程学院， 四川 成都 610031)

0 引 言

反曲弓是一种主要通过弓体形变积蓄弹性势能，再通过自身结构部件传递给箭矢，达到势能向动能转化，并推动箭矢射击的武器.根据形制不同，反曲弓大体被分为传统和现代反曲弓两大类[1-2].反曲弓弓臂作为主要的形变蓄能部位，过去大多由牛角、层压片等高弹性传统材料制成，近年来，玻璃钢片作为替代品被大量应用，但因其多余震动大、能量转化效率低等不足而饱受诟病.对此，人们采取多种减震措施提高射击效率和安全性[3-4].目前，通过对玻璃钢片弓臂不同部位进行磨薄处理，减少多余震动以提高能量转化效率，被称为渐薄工艺.但受制于成本因素，玻璃钢制传统反曲弓的渐薄应用仍旧处于经验导向阶段，一直缺乏科学的定性分析[5-7].基于此，本研究通过理论研究与实验分析，不同的弓臂渐薄方案对于能量转化效率的影响，着重考察弓臂的渐薄部位和深度2个指标，旨在揭示渐薄工艺对于弓箭能量转化效率的影响规律.

1 有限元研究

1.1 有限元模型建立

本研究中使用的玻璃钢片尺寸为1 200 mm×30 mm×5 mm，弹性模量为3E4 MPa，泊松比为0.03.弓梢和弓把尺寸如图1所示.弓梢和弓把材料为硬质木材，设置弹性模量为640 MPa.因成年人的开弓拉距约为600 mm，故本研究将反曲弓的拉距定为600 mm.

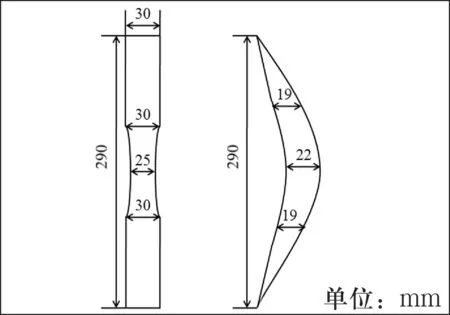
(a)弓把

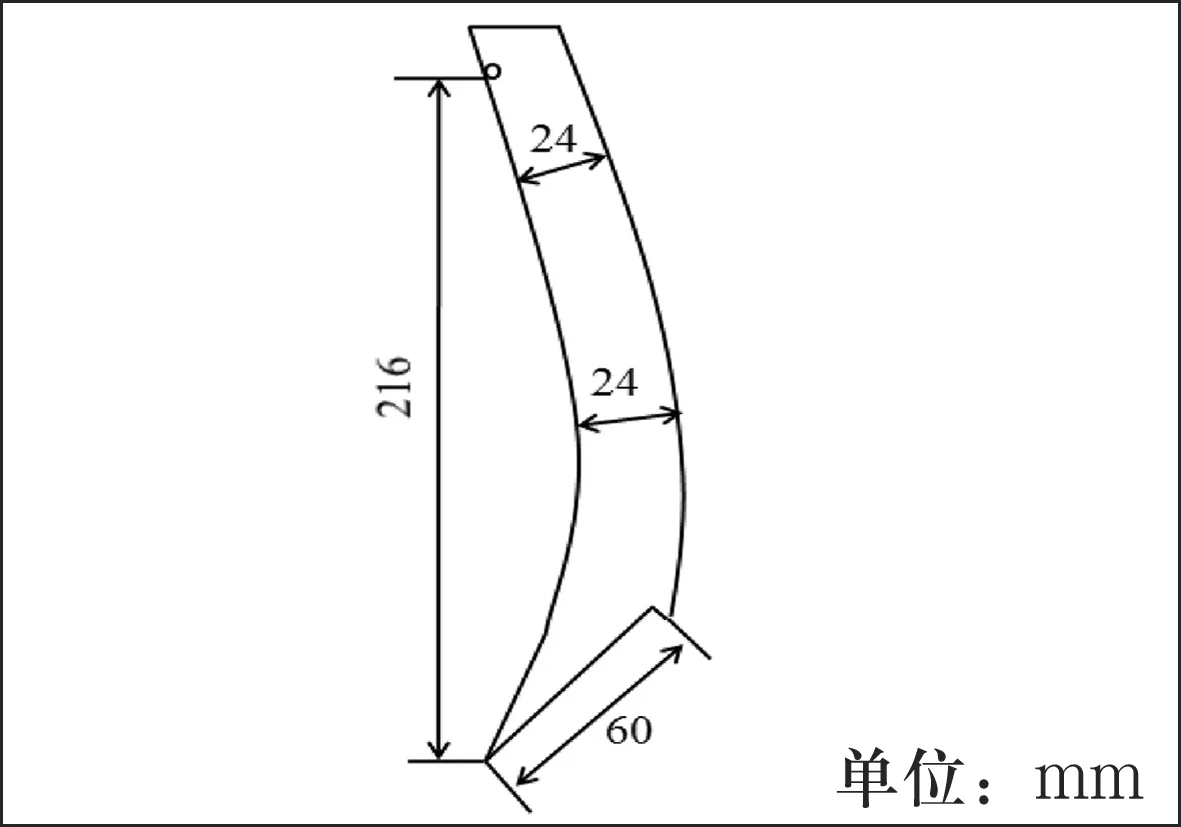
(b)弓梢尺

图1反曲弓相关部位尺寸示意图

本研究中，反曲弓的弓臂长度为390 mm.建立如图2所示的尺寸标示，设弓把与弓臂结合点距离渐薄起始点长度为X，渐薄长度为L，渐薄结束点距离弓梢弓臂结合点长度为Y，渐薄深度为H.弓臂渐薄处理主要包含打磨渐薄的深度和打磨渐薄的部位两方面.设有1组对照模型0#(未作渐薄处理)，以及6组实验组模型1#～6#.通过改变X值和Y值来确定渐薄处理部位，通过改变H值来确定渐薄深度，模型具体数据如表1所示.

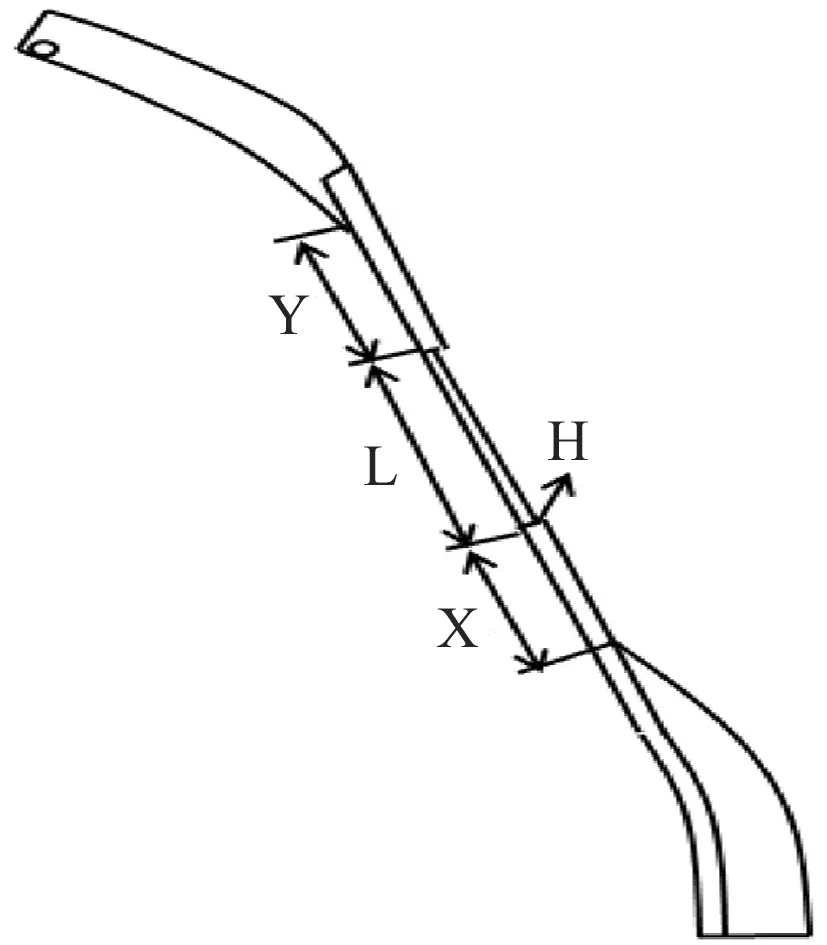
图2反曲弓弓臂渐薄尺寸标示图

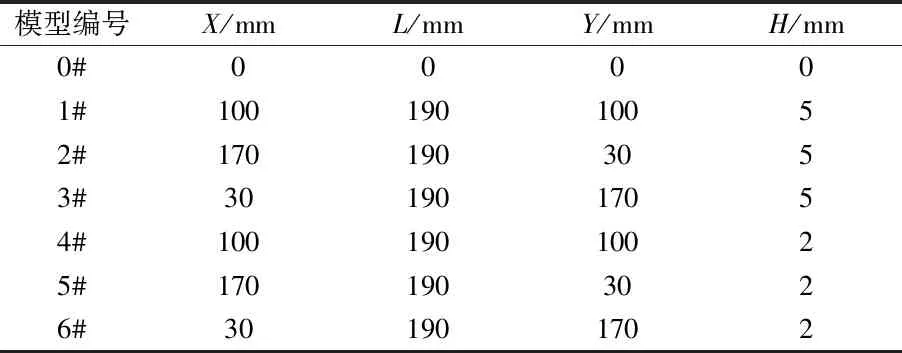
表1 反曲弓弓臂理论模型尺寸

因本研究主要分析弓臂渐薄的影响，故对反曲弓的其他部位进行如下简化处理：弓梢、弓把与弓臂连接处以高强度胶粘和轮胎线固定方式连接，长度较短，变形量小，故将其视为刚性连接；弓弦为理想绳索，长度为135 cm；箭矢视为质点，耦合在弓弦中部；因反曲弓是上下对称结构，为降低计算量，建模中只建立上半部分.同时，在有限元模型中，弓臂部分采用solid-shell190单元，弓梢弓把处用solid185单元，弓弦采用link180单元，箭矢采用mass21单元，反曲弓仿真模型及细节展示如图3所示.

模拟分析过程分为静态和动态加载两部分：静态加载部分是将反曲弓由上弦后状态进行拉伸，计算反曲弓在0～600 mm拉距下的拉力数据，并计算理论弹性势能大小；动态加载部分则是通过将弓弦在拉距为600 mm处释放，获取反曲弓恢复到无加载状态时模拟箭矢质点的速度，计算该工况下的动能.

1.2 能量转化效率

反曲弓在开弓过程中积蓄的弹性势能值可以表示为，

(1)

式中，F为不同拉距下的拉力值，L为最大拉距.

箭矢射击后所具有的动能EkA为，

(2)

式中，mA为箭矢的质量，VA为箭矢射击出去后所具有的速度.

弓箭的能量转化效率ε为，

(3)

理论速度VB是假定弹性势能能量全部转化为动能时，箭矢应具有的速度VB为，

(a)反曲弓仿真模型图

(b)反曲弓弓梢弓臂连接方式示意图

(c)反曲弓弓臂弓把连接方式示意图

(d)反曲弓渐薄实现形式示意图

图3反曲弓仿真模型及细节展示

(4)

运用式(1)～式(4)对拉力数据处理，可以求得弓箭的能量转化效率，并量化分析不同渐薄方案对于能量转化效率的影响.

1.3 模拟分析结果

有限元模型模拟的拉力曲线如图4所示，能量转换效率如表2所示.

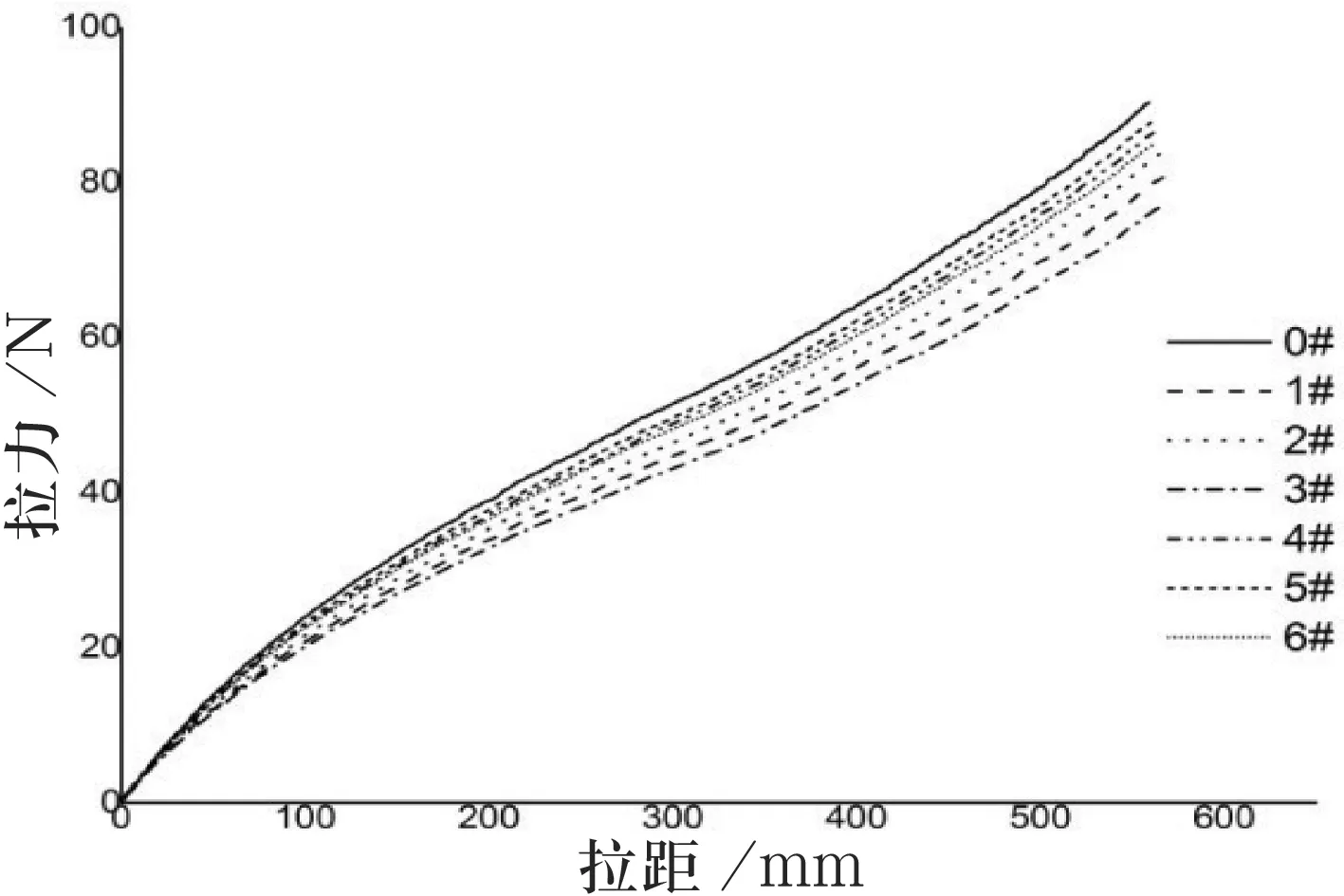
图4 理论计算的拉力曲线

结合图4和表2可知，反曲弓的弓臂渐薄对弓箭的能量转化效率具有较大影响.将模型1#、2#、3#与对照组模型0#进行比对可发现，当渐薄部位靠近弓把处时，弓箭效率可以得到明显提高，同时反曲弓的最大拉力也有较大下降；当渐薄部位靠近弓梢处时，反曲弓的效率会逐步下降；当渐薄部位足够靠近弓梢时，反曲弓的能量转化效率反而低于未做渐薄处理的对照组.同时，对模型1#、2#、3#和模型4#、5#、6#进行对比可知，当渐薄深度增加时，能量转化效率会有所提高，但弓箭最大拉力会出现衰减.模型2#、3#的应力云图如图5所示.

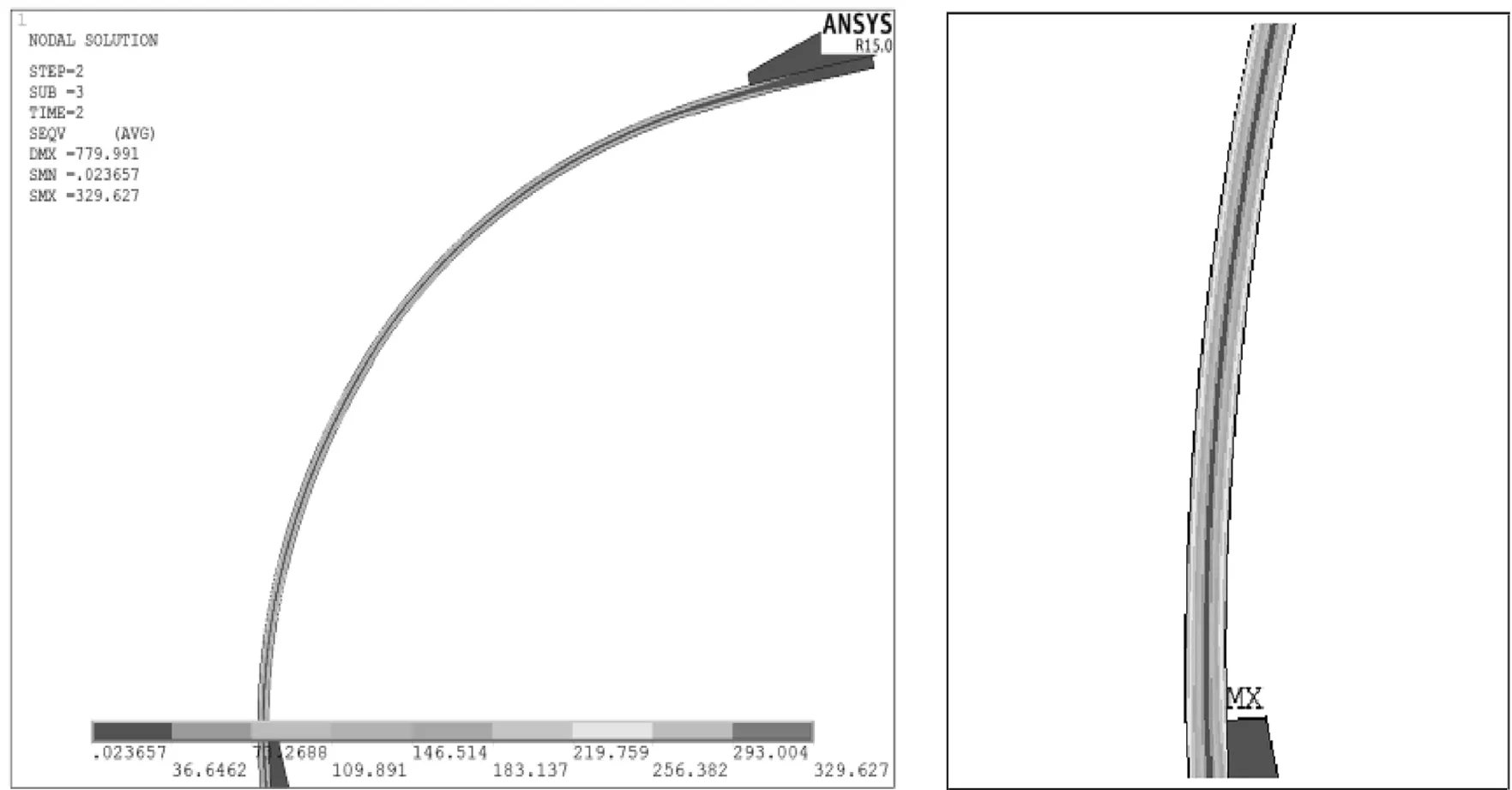
(a)模型2#应力云图

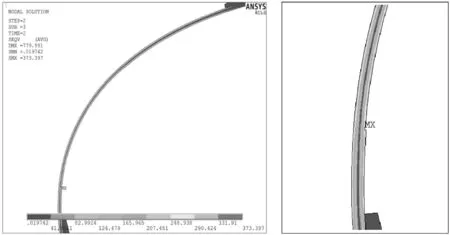
(b)模型3#应力云图

图5模型应力云图

由图5可知，弓臂主要变形部位靠近于弓把，弓臂双侧应力皆由弓把处向弓梢处逐步减小.对弓臂进行渐薄处理能使弓臂的应力分布得到有效改善.当渐薄部位更靠近弓把处时，即当XY时，则在靠近弓把处应力分布较为集中，整个弓臂应力分布极不均匀.极端情况下，在靠近弓梢处做渐薄处理，会造成对弓梢的支撑不足，射击过程中使弓梢产生过多震动，降低了反曲弓的能量转化效率.

2 实验分析

2.1 实验模型

本研究设计的实验装置的示意图见图6，选取台虎钳作为夹具夹持反曲弓弓把，将反曲弓固定于实验台上，拉力器一端绑定在弓弦中部，另一端与绞盘相连.通过绞盘牵拉使反曲弓张开到不同的拉距，读取不同拉距下拉力计数据，进行拉力曲线测绘，并通过测速仪对600 mm拉距下的箭速进行测试.

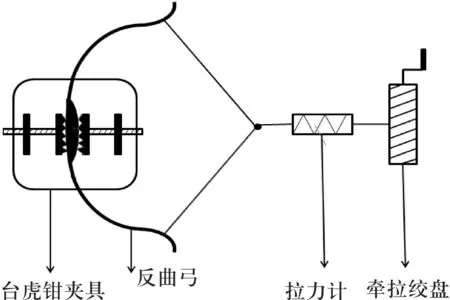
图6拉力曲线测试夹具示意图

通过对6组实验组和1组对照组模型的数据分析，初步得到了不同渐薄方案对弓臂能量转化效率的影响规律，并确定5 mm为较好的渐薄深度设计，选取模型0#～3#的尺寸数据制作实验弓.

2.2 实验结果

在实验中，对4种反曲弓模型进行测试，将测得拉力数据绘制成拉力曲线，具体如图7所示.

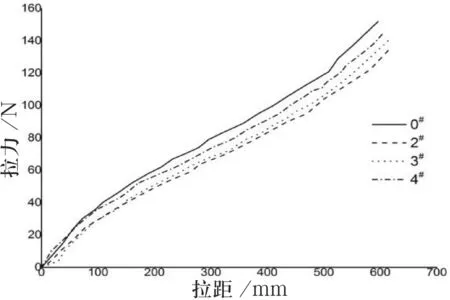
图7实验模型的拉力曲线

同时，根据式(1)、式(3)，计算出反曲弓模型的弹性势能以及能量转化效率，如表3所示.表3中将实验测试的能量转化效率(ε2)与模拟计算的能量转化效率(ε1)进行了对比.

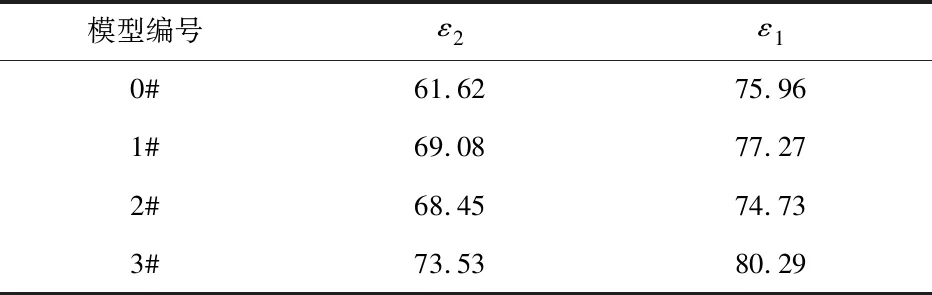
表3 实验数据(/%)

由表3可知，理论数据与实验结果趋势吻合较好，但由于实验中的能量耗散而导致理论计算效率值较实验值普遍偏高.同时，由于模型3#的渐薄更靠近弓把，该模型的能量转化效率约为73.53%，较模型0#能量转化效率有较明显的提高；模型1#的能量转化效率次之；由于模型2#的渐薄靠近弓梢，其转化效率较低，但是能量转化效率仍然高于对照组0#.证明了在弓把处做渐薄处理能够更好地提高能量转化效率的假设是正确的.但对于靠近弓梢处的渐薄的能量转化效率的预测还不够准确.通过观察图12中的拉力曲线发现，对弓臂进行合适的渐薄处理，曲线后段拉力增长更为平缓，能够有效的提高弓箭手射击时的舒适度，这也是渐薄处理过的弓后段拉感更为柔和舒适的原因.

3 结 论

本研究通过理论计算与实验分析，对于玻璃钢片反曲弓的渐薄问题，可以定性地得出以下结论：对玻璃钢反曲弓的弓臂内侧做渐薄处理，能有效地提高能量转化效率；渐薄部位越靠近弓把，能量转化效率越高；靠近弓梢处的渐薄处理，对能量转化效率的提升有限；对弓臂进行适当的渐薄处理，可以有效降低反曲弓拉力曲线后段的增长率，提高反曲弓的拉感.