轴向气流下曲壁板气动压力的理论与实验研究

李 晋， 李 鹏， 代成栋， 范晨光， 杨翊仁

(1.成都双流国际机场有限公司 资产管理部， 四川 成都 610202；2.西南交通大学 力学与工程学院， 四川 成都 610031)

0 引 言

近年来，曲壁板结构被大量使用在高速列车及土建工程中等.但当这类结构处在轴向气流的作用下时，气流会与结构而产生较为强烈的耦合作用，使结构产生振动，并引起结构的疲劳损伤以及减少其使用寿命[1-2].相关研究表明，对壁板结构流固耦合振动的研究，准确获取结构在轴向气流作用下所承受的气动压力对实际工程设计与应用尤为重要[3-4].

目前，针对壁板结构的气动力研究主要集中在超音速范围内，尤其以活塞理论气动力模型[5-7]为主流研究模型.由于曲壁板的初始构型所受到的静态气动力对系统的动力特性有着非常重要的影响，而现有的针对曲壁板气动力的研究多是以理论气动力为主，缺少相关的风洞实验的具体数据对比分析.对此，本研究拟采用势流的点源基本解来获取轴向气流下曲壁板气动力的近似表达式，并设计完成了相关的风洞实验，同时将本研究理论计算结果与实验结果及已有文献的理论结果进行对比，验证了本研究理论解的准确性.

1 理论分析

考虑如图1所示两端固定的二维曲壁板，该壁板上表面有沿轴向的气流.气流的流速及密度分别为U∞与ρ∞，壁板具有的初始构型函数W(x).考虑无黏无旋不可压缩的气流，基于势函数点源形式的基本解及边界条件，有，

(1)

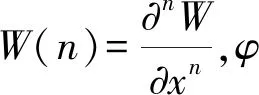
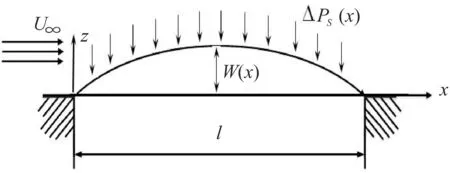
图1轴向气流下的曲壁板模型

由伯努利方程可得壁板上表面的压强为，

(2)

将式(1)带入式(2)可得，

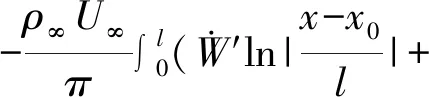
(3)

对式(3)的后半部进行分部积分后可得，

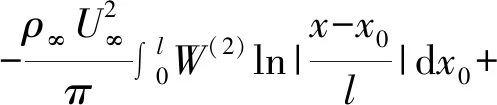
(4)

将式(4)的前半部分在x0=x处进行泰勒展开，其动态气动力ΔPs为，

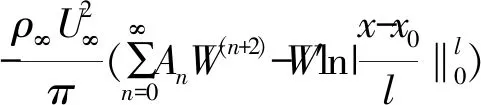
(5)

式中，

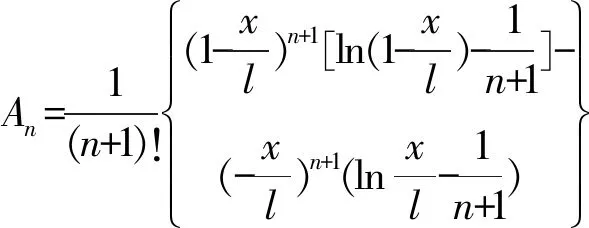
(6)

式(5)中，第一项表明壁板表面的压力与初始变形曲率相关，最后一项表明结构的边界条件对气动力有着重要的影响.

由式(6)给出的气动力系数如图2所示.

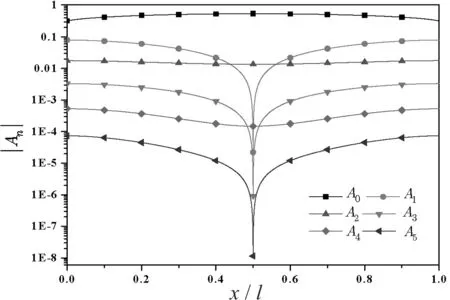
图2气动力系数曲线

从图2可知，当n为偶数时，气动力系数呈对称分布，而当n为奇数时其呈反对称分布.

在本研究中，视壁板为无限长波形壁板的一部分，利用模态展开法，作用在壁板的气动力为，

(7)

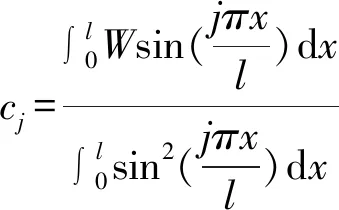
2 实验研究

为了验证式(7)给出的气动力计算公式的准确性，本研究设计并完成了相关的风洞实验.在实验中，采用厚度为2 mm的铝合金板加工成两组不同初始构型的曲壁板(分别记作：I、II)，两组曲壁板实际的初始构型及其拟合曲线如图3所示.

同时，沿着壁板中轴线开有5个直径为2 mm的小孔用于安装压力传感器(XCQ-062)，压力传感器采用橡皮泥固定在壁板背面，其安装如图4(a)所示.为保证曲板仅受单侧轴向气流作用，壁板结构安装在导流装置上.该装置由一个近似封闭的空腔构成(空腔内填充有海绵，内部流体并可视为静止)，其前导流面与前缓冲区域可以保证在流场受大的扰动后流经壁板模型处仍为均匀流场，而后导流面与后缓冲区可以使壁板模型避开尾流的影响.该导流装置安装在刚性风洞支架上，曲板两端固定并将上下两侧用胶布封闭，其安装方式如图4(b)所示.

图3曲壁板初始构型及其拟合曲线图

图4压力传感器安装示意图

实验所采用的风洞设备是直径为1.2 m的开口环流式风洞，曲壁板实验安装如图5所示.该风洞优质的稳定实验风速区间为15～30 m/s.实验中使用的数据采集仪器有INV1861A应变调理器以及INV3062T0云智慧采集仪.将压力传感器连接至应变调理器，并将应变调理器连接至云智慧采集仪.

3 实验结果

本研究对两组实验曲壁板模型进行了风洞吹风实验，并在不同的稳定风速下采集3组数据，分别记为1、2、3，以此计算出每组风速下的压力平均值(avg)作为最终的实验结果.

图5曲壁板实验安装图

1)不同风速下两组曲壁板模型上各点压力分布随风速变化情况如图6所示.

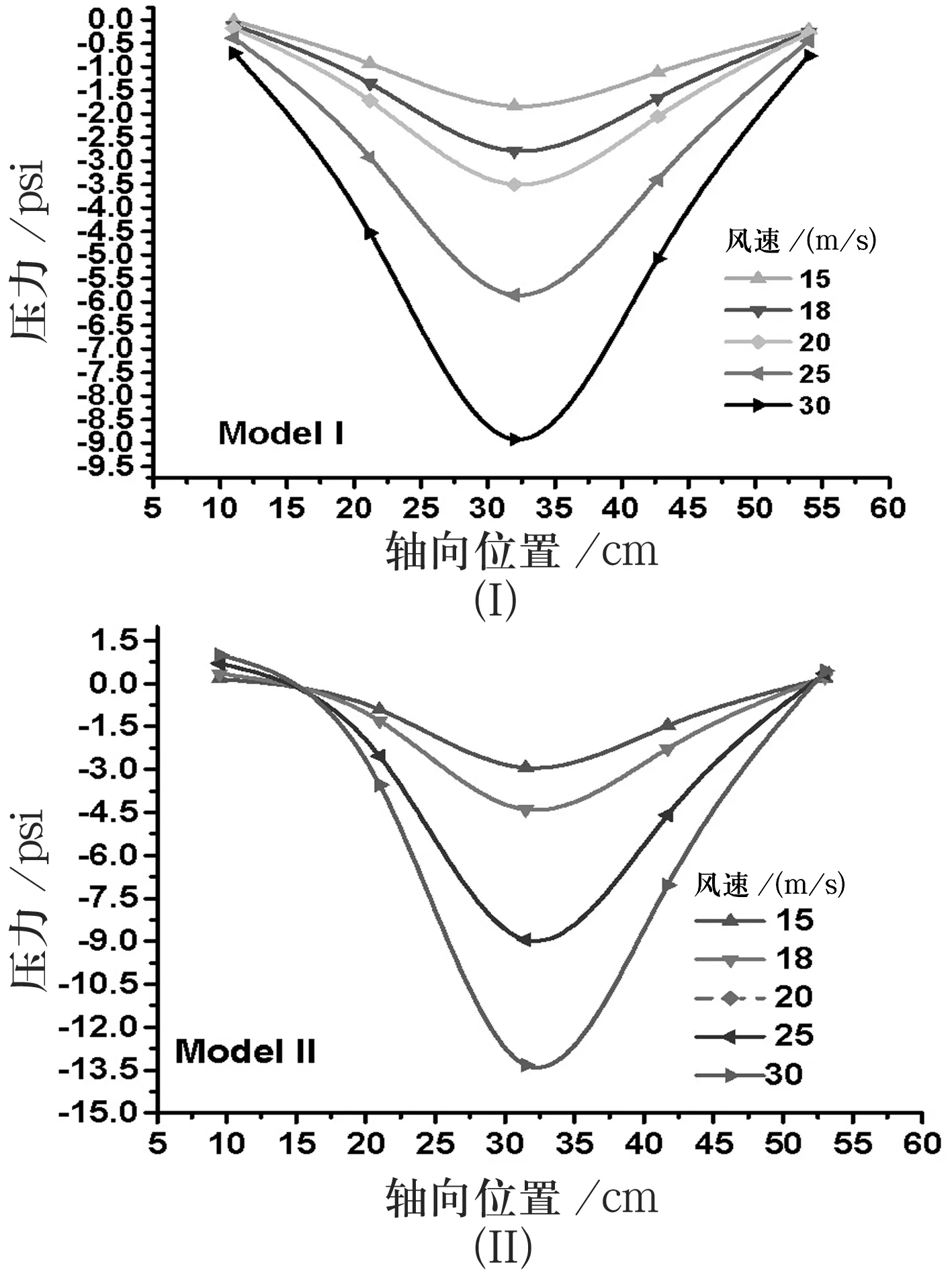
图6曲壁板压力随风速变化图

由图6可知，曲壁板表面受到负压力的作用，压力沿着曲壁板中点呈现近似对称分布，压力的最大值出现在静变形最大的位置处.

2)相同风速下，两组曲壁板模型表面的压力对比如图7所示.

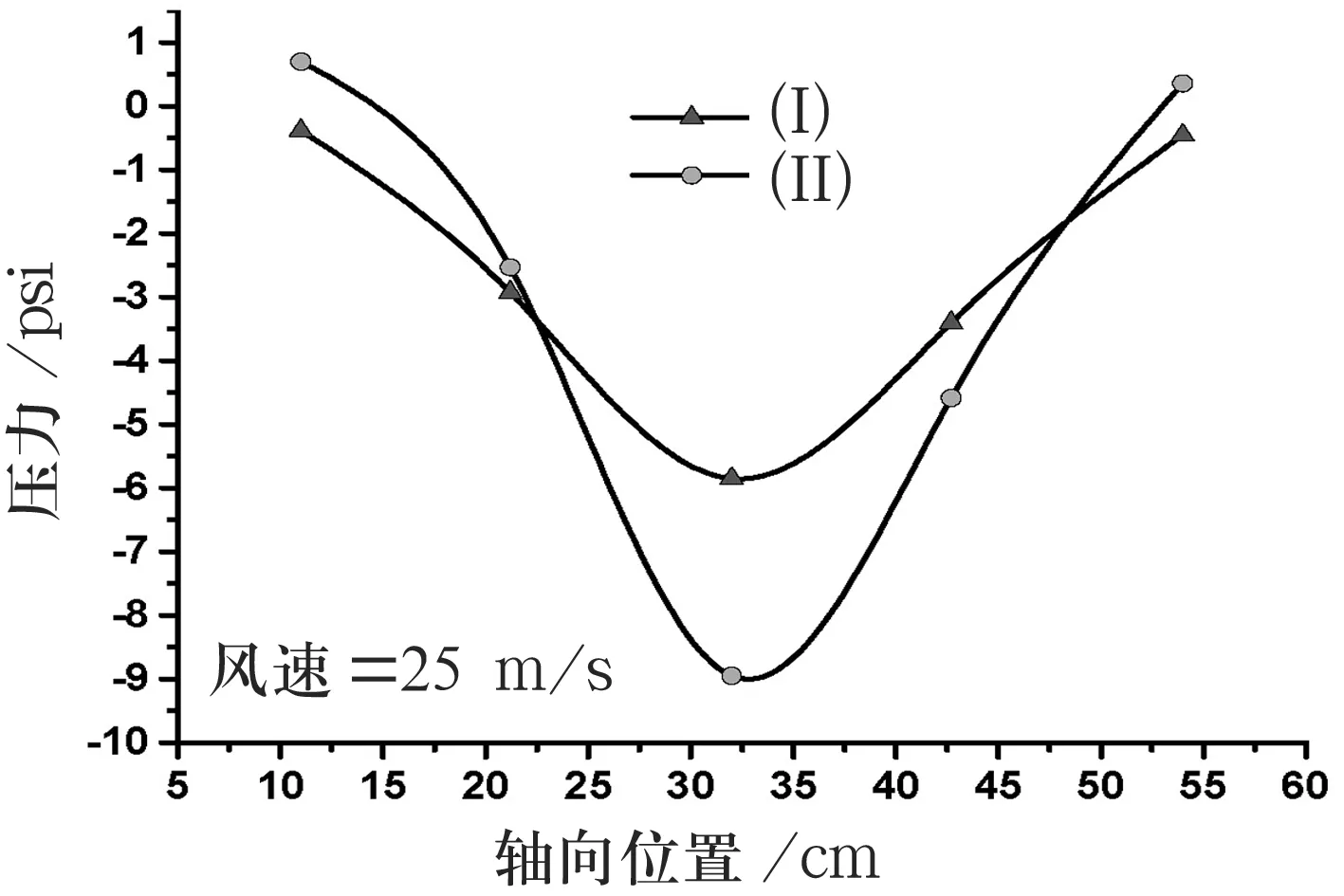
图7 两组曲壁板模型的压力对比图

由图7可知，壁板的初始曲率越大，负压越大.

3)两组曲壁板模型上各测试点的压力系数Cp随风速的变化趋势如图8所示.

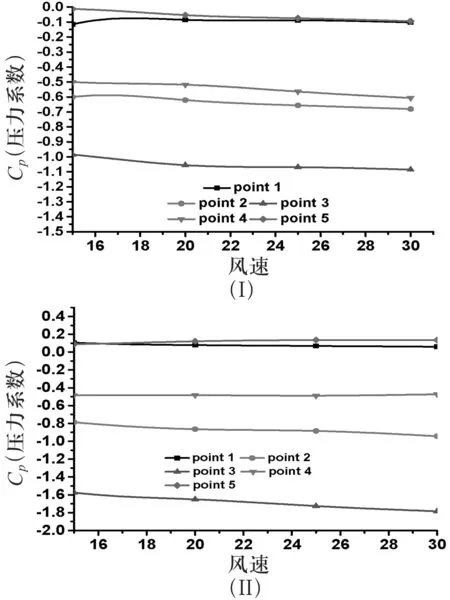
图8曲壁板压力系数Cp随风速变化图

从图8可知，曲壁板第3个测试点的压力系数在不同的风速下均保持稳定，且初始曲率越大的点处的压力系数越大.由于测点1与5，2与4呈近似对称分布，因此这些点对应的压力系数也近似相等.

4 理论与实验对比分析

本研究针对两组曲壁板的初始构型采用多项式拟合，可得其对应的近似构型函数，如图3中虚线所示.两组模型对应初始构型函数分别为，

W1=3.854 2x4-5.086 4x3+1.732 4x2-0.036 1x+0.003

W2=6.876 9x4-8.495x3+2.605 5x2-0.011 8x+0.000 3

(8)

将上述两组初始构型函数(8)带入式(5)、式(7)可得到两种气动力公式的理论计算结果，分别记为ΔPs1及ΔPs2.计算时，式(6)、式(7)中的n分别取为2和4，两种理论计算结果如图9所示.

由图9可知，与文献[8]相比，本研究的计算结果与实验结果吻合更好，更能够准确地反映壁板结构上的压力分布.需要指出的是，在壁板前后缘处理论计算与实验结果有一些偏差，在以下的计算中，曲壁板前后缘均有固定约束，其对系统稳定性不会产生明显影响.事实上，这种偏差主要是由于理论计算中并未计及前后刚性导流段的影响，这也是作者正在开展的工作.

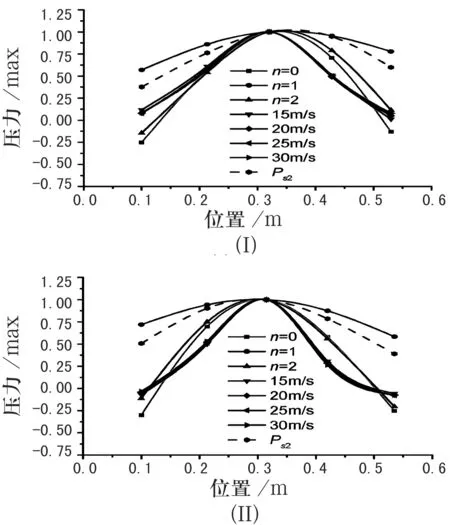
图9理论计算与实验结果对比图

同时，图9还展示了式(5)中不同求和项数n对气动力计算结果的影响.结果表明，针对两组曲壁板模型，当n=0，2时，理论结果均与实验结果吻合较好，这也说明式(5)中第一项占主导成分，与文献[7]的研究结果一致.而当n=1时，两者结果吻合程度较差，这主要是由于A1呈现反对称分布，如图2所示，这与曲壁板的近似对称的初始变形相反.

5 结 论

1)在轴向气流作用下，曲壁板表面出现较大的近似对称的负压区，且压力值随风速的增大而增大；相同风速下，压力值随初始曲率的增大而增大.

2)本研究所给出的气动压力计算方法与实验结果吻合良好，表明了该计算方法的合理及准确性.