考虑钢梁扭转的大悬挑雨篷设计实例分析

唐 宽

（中信建筑设计研究总院有限公司，湖北 武汉 430014）

0 引言

由于钢结构设计标准[1]（GB50017-2017）对钢梁的扭转计算及抗扭构件设计并未作出明确的规定，因此在实际工程中常常被设计人员忽略，或者常常仅对扭转采取一些构造措施，带有一定的盲目性。而事实上，当钢梁面没有楼板的有效约束时，扭矩对梁的应力影响不容忽略的。

本文通过一个钢结构雨篷设计的实例，比较两种不同截面（箱型截面和H 型截面）的钢梁受扭的应力情况，供设计人员参考。

1 工程概况

1.1 钢雨篷的平面形式

本实例为一跨度8.75m 的悬挑雨篷，柱间设置两道主梁，雨篷悬挑梁与两道主梁垂直相交，并伸入靠内的主梁。恒荷载取2kN/m2，活荷载取5kN/m2，钢材材质均采用Q345B。雨篷钢梁布置见图1。

1.2 钢雨篷的截面参数

雨篷梁均采用箱型截面。GL22e：B700x300x40x40。GL22f：B700x400x40x40；GL22g：B700x200x20x20；GL22h：B350x400x20x20；GL22k：B(700～350)x250x30x30；GL22j：B700x250x30x30。

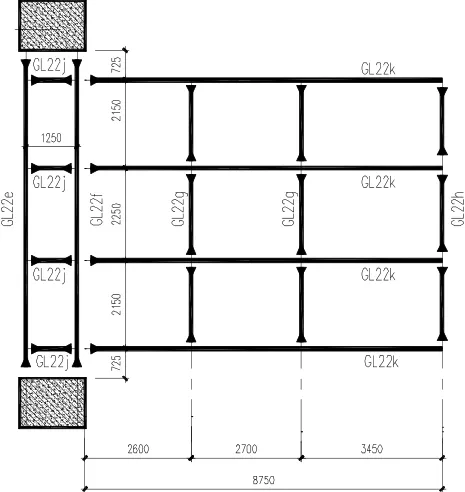
图1 雨篷钢梁平面布置图

2 Midas Gen 分析结果

由建筑结构静力计算实用手册[2]（第二版），Mt 为纯扭矩，Mw 为翘曲扭矩，Mb 为弯扭双力矩。Mt 和Mw 产生纯扭剪应力和翘曲剪应力，Mb 产生翘曲正应力（见图2）。

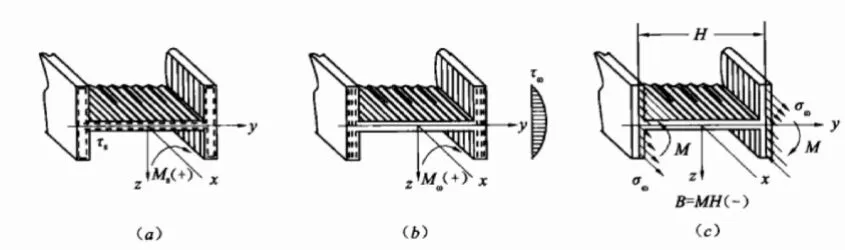
图2 钢梁扭转内力图

以GL22j、GL22k 及GL22f 交接节点作为分析对象，

由于钢梁应力综合应力最大的位置为GL22f 与柱连接节点处，取GL22f 梁端截面处的应力（表1）：

表1 GL22f 梁端最大应力

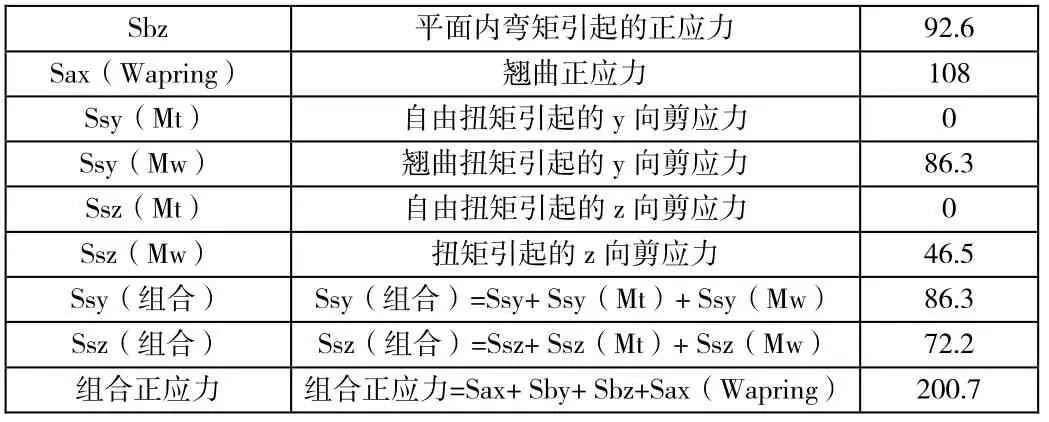
Sbz 平面内弯矩引起的正应力 92.6 Sax（Wapring） 翘曲正应力 108 Ssy（Mt） 自由扭矩引起的y 向剪应力 0 Ssy（Mw） 翘曲扭矩引起的y 向剪应力 86.3 Ssz（Mt） 自由扭矩引起的z 向剪应力 0 Ssz（Mw） 扭矩引起的z 向剪应力 46.5 Ssy（组合） Ssy（组合）=Ssy+ Ssy（Mt）+ Ssy（Mw） 86.3 Ssz（组合） Ssz（组合）=Ssz+ Ssz（Mt）+ Ssz（Mw） 72.2 组合正应力 组合正应力=Sax+ Sby+ Sbz+Sax（Wapring） 200.7

由以上表格可见，y向剪应力Ssy（组合）全部是由扭矩引起的，Ssz向剪应力ssz（Mw）为46.5，占Ssz（组合）72.2的64.4%。由扭矩引起的正应力值Sax（Wapring）为108N/m2，占钢梁组合正应力200.7的53.8%。

3 H 型截面计算分析

同样的计算条件，我们将所有钢梁均等截面高度及等翼缘腹板厚度的H型截面。

Midas 计算结果内力如下表2：

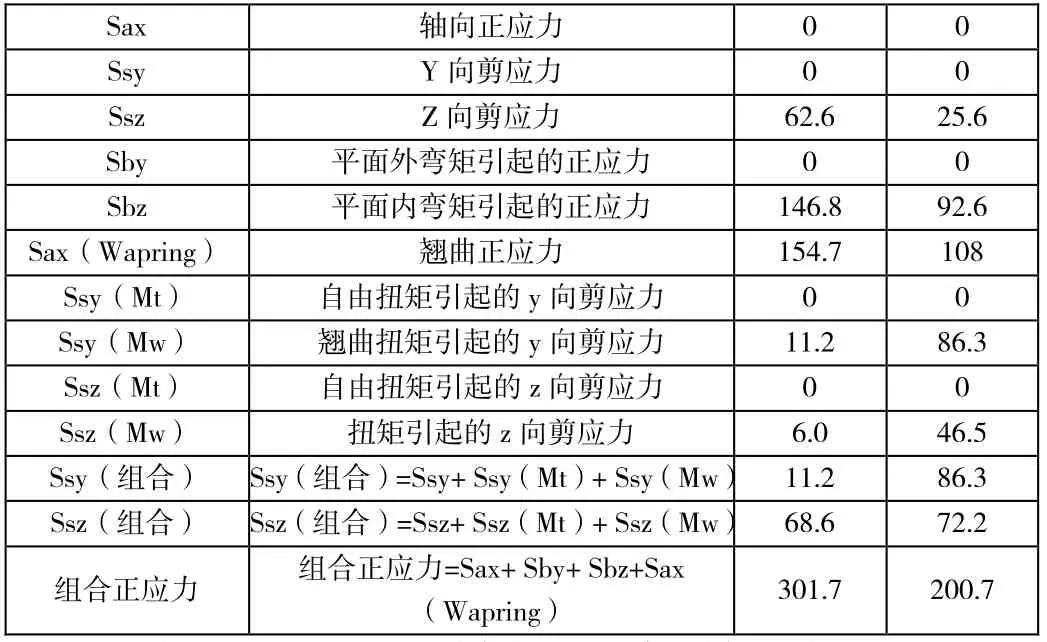
表2 GL22f 梁端最大应力

且以上表格可见，H 型梁y 向剪应力Ssy（组合）全部是由扭矩引起的。Z 向剪应力基本由Z 向剪力产生。由扭矩引起的正应力值Sax（Wapring）为154.7N/m2，占钢梁组合正应力301.7 的51.3%。

4 小结

(1) y 向的剪应力均全部由纯扭矩及翘曲扭矩产生。

(2)z 向的剪力由竖向力、纯扭矩及翘曲扭矩共同产生。

(3)悬挑端负弯矩的传递，与钢梁的抗扭刚度相关，箱型梁抗扭刚度明显大于H 型梁，因此Mx 分担的比例也较大。

(4)两种钢梁型式中，翘曲正应力Sax（Warping）在组合正应力中的比例都超过50%。因此在工程应用中，扭矩产生的翘曲正应力不容忽略，否则会有严重的安全隐患。

(5)在相同荷载及支座条件下，同样截面参数的箱型截面抗扭能力明显高于H型截面。因此，工程中的作为抵抗扭矩的构件应更推荐采用箱型截面。