基于Berg模型橡胶衬套的汽车平顺性分析

张艳龙，李 彪，王 丽，孙绍轩

(1.兰州交通大学 机电工程学院，兰州 730070；2.中国铁路兰州局集团有限公司 兰西车辆段，兰州 730070；3.兰州城市学院 数学学院，兰州 730070)

随着汽车行驶平顺性的研究日益受到重视，需要分析出影响汽车行驶平顺性振动响应量的主要因素，进而提出改进的方法措施。而现代汽车悬架系统中大量应用橡胶衬套等弹性元件，其对于改善悬架弹性运动学性能、有效减弱路面不平度激励引起的振动发挥重要作用。陶向华等基于人-车-路相互作用建立简化的3质量车辆模型，利用所建的简化车辆模型对车辆的振动特性进行了评价[1]。李杰等基于虚拟激励法，推导1/2汽车4自由度系统振动的频率响应特性，建立求取汽车系统振动响应量及其功率谱密度的公式，给出了求解汽车振动响应量功率谱密度的算例[2]。徐中明等依据国际标准ISO2631，对某客车进行行驶平顺性试验，研究了时、频两种算法在平顺性分析中的差别[3]。于增亮等针对目前应用的Kelvin-Voigt模型、3参数Maxwell模型、Berg模型和DZIERZEK模型进行模型结构特征、参数识别方法与特性预测精度的对比分析[4]。左曙光等建立一种能准确描述其动态特性的理论模型，通过试验得到了橡胶衬套轴向的静、动态特性，对其频率相关性和振幅相关性进行了分析[5]。目前单独研究橡胶衬套的材料性能较多，将非线性衬套与车辆振动相结合的研究相对较少[6-14]。

为了更好体现出橡胶衬套动态特性的振幅依赖性，本文应用Berg模型描述橡胶衬套的摩擦效应，建立含有摩擦特性的3自由度车辆垂向模型，分析Berg模型摩擦特性对车辆振动响应量和人体加权加速度均方根值的影响，进而分析橡胶衬套对汽车平顺性的影响。

1 含有摩擦特性的车辆振动模型

为了分析基于Berg模型的橡胶衬套对汽车平顺性的影响，建立如图1所示的含摩擦特性的3自由度车辆垂向振动模型。

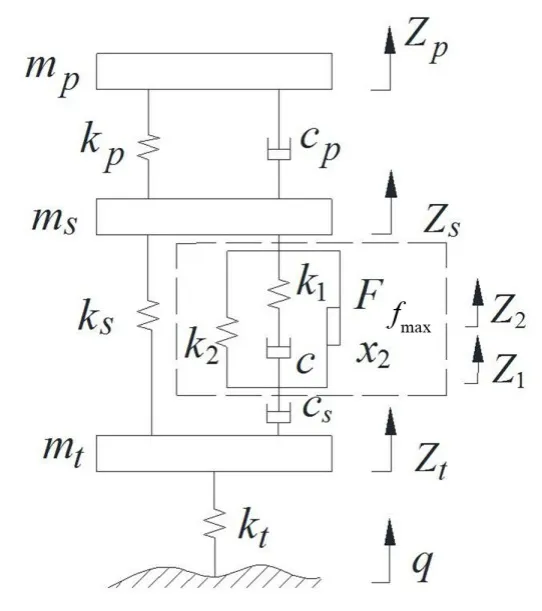
图1 车辆振动模型

图中mp为人体质量之半，ms为车身部分质量，mt为轮胎质量，其值分别为30 kg、230 kg、30 kg；kp为座椅刚度之半，ks为车身悬架刚度，kt为轮胎刚度，其值分别为9950 N/m、20200 N/m、128000 N/m；cp为座椅阻尼之半，cs为悬架阻尼，其值分别为264 N·s/m、1137 N·s/m(考虑到车辆左右对称，在车辆模型参数选取时，mp、kp和cp分别为人体质量、座椅刚度和阻尼之半[1])；zp、zs、zt、z1分别为人体垂直位移、车身垂直位移、车轮垂直位移及摩擦单元垂直位移，z2为串联弹簧k1与串联阻尼c之间的垂直位移，单位为m；q表示为路面不平度，单位为m；图1虚线框内所示为Berg模型，Ff为Berg模型中的摩擦力，单位为N；k1、k2、c1、x2的取值见表1。

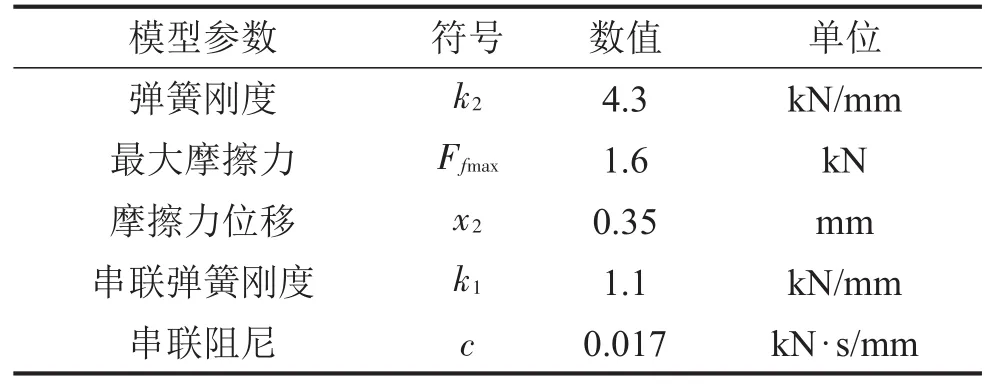
表1 Berg模型参数

由拉格朗日方程可得到3自由度车辆模型的微分方程组为

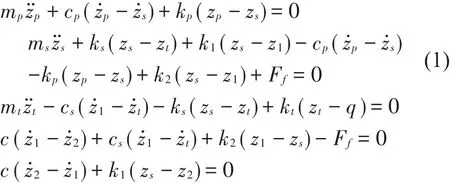
Berg模型的摩擦力Ff取决于摩擦单元两端的相对位移，同时也与摩擦力位移曲线上的参考点(xs,Ffs)有关，其具体表达形式为

当x=xs时，

当x＞xs或x增加时

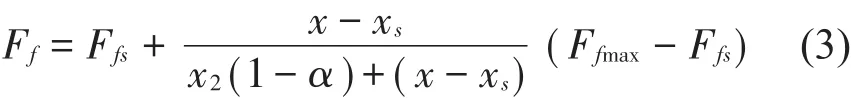
当x＜xs或x减小时

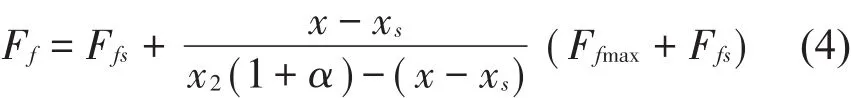
其中：Ffmax为最大摩擦力；x2为摩擦力Ff从0开始逐渐增加至Ff=F∕2时的位移值

fmax取值为-1～1。

国际标准化组织建议路面功率谱密度Gq(n)用下式作为拟合表达式

式中：n为空间频率，单位m-1，它是波长的倒数，表示每米长度中包含几个波长；n0为参考空间频率，n0=0.1m-1；Gq(n0)为参考空间频率n0下的路面功率谱密度值，称为路面不平度系数，单位为m2∕m-1=m3；w为频率指数，w=2，为双对数坐标上斜线的斜率，它决定路面功率谱密度的频率结构。

用三角级数法对路面进行模拟作为车辆振动输入。以B级路面为例，车速v为20 m/s，仿真结果如图2所示。

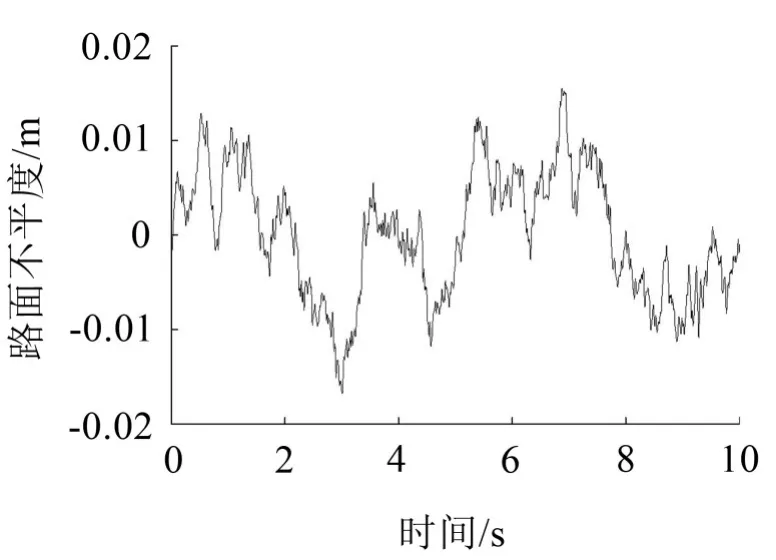
图2 B级路面随机激励

2 车辆振动仿真分析

将车辆振动方程组转换成状态方程，并结合路面随机激励，采用4阶龙格库塔法进行数值积分可得到响应的时间历程曲线，并通过FFT变换得到相应量的功率谱密度曲线。

2.1 汽车振动响应量的仿真分析

图3(a)和图3(b)分别为系统在时域中的人体加速度和悬架动挠度的仿真曲线。从图中可以看出：相较于未考虑橡胶衬套，考虑橡胶衬套时曲线值在不同程度上都有所减小。在图3(a)中，当t在1.1 s和6.7 s时，2个振动加速度的峰值都明显减小，并且当考虑橡胶衬套时，人体振动加速度基本都在-1 m/s2～1 m/s2之间。在图3(b)中，当t在0～2 s区间内，可以明显发现在考虑橡胶衬套时悬架动挠度都大幅度减弱，在考虑橡胶衬套时悬架动挠度也基本在-0.008 m～0.008 m之间。可以得出，在考虑Berg橡胶衬套的摩擦特性后，汽车在时域上的振动响应量都有不同程度减小，说明其有效地减弱了振动。

对时域响应量进行FFT变换可以得到其对应的功率谱密度曲线，如图4(a)和图4(b)所示。

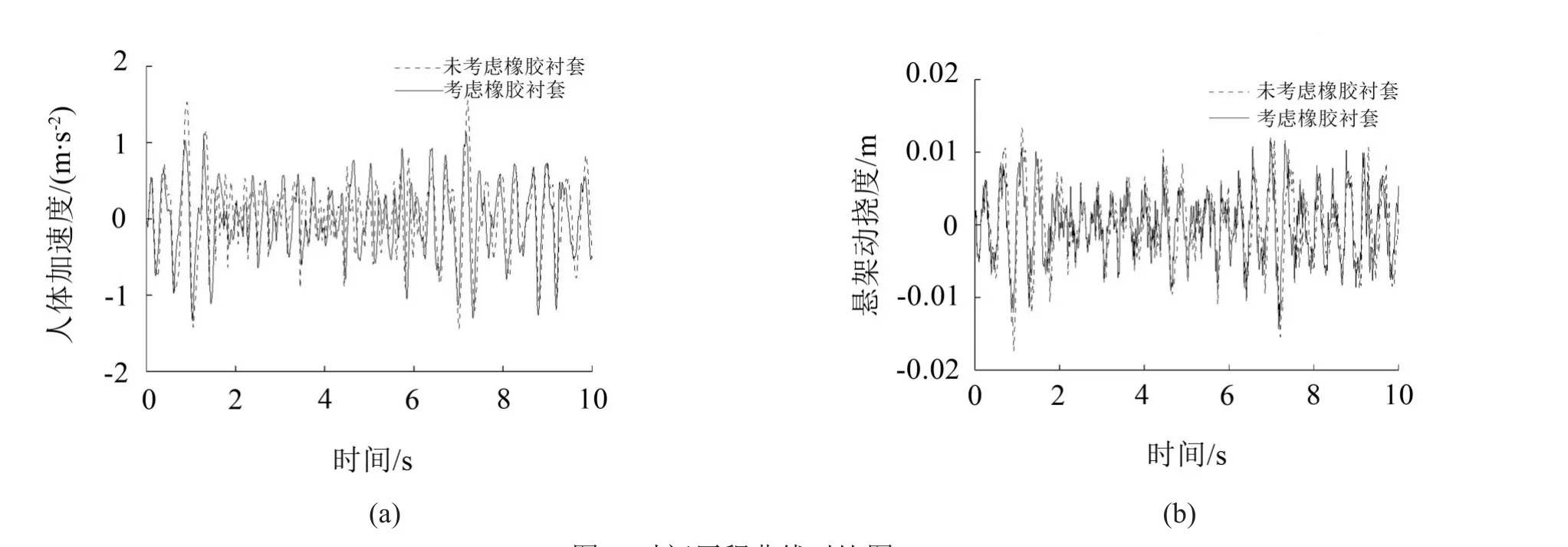
图3 时间历程曲线对比图

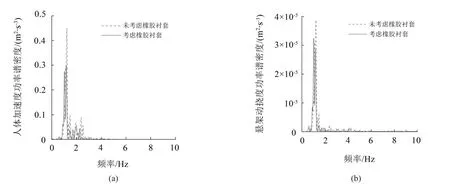
图4 功率谱密度曲线对比图

在图4(a)中，由人体加速度功率谱密度图可知：未考虑橡胶衬套时和考虑橡胶衬套时的共振频率分别为1.22 Hz和1.17 Hz，可见橡胶衬套的摩擦特性使人体的共振频率减小了4.1%。同时也可以看到，在考虑橡胶衬套后人体加速度功率谱幅值降低33%。图4(b)为悬架动挠度功率谱密度图，可以得出在未考虑橡胶衬套和考虑橡胶衬套后的共振频率分别为1.21 Hz和1.03 Hz，此外在考虑橡胶衬套后悬架动挠度功率谱幅值降低16%。可以得出，在考虑Berg橡胶衬套的摩擦特性后，汽车在频域上振动响应量的功率谱密度值也都在不同程度减小，尤其是在幅值处减小更显著，说明其消耗了振动能量。

2.2 Berg模型参数对人体加速度的影响

图5是Berg模型中k1、k2和c3个参数在原值及原值的1.5倍、0.5倍时人体加速度时间历程曲线。从图5(a)中可以看到，当k1值较小时在时间历程曲线中的对应峰值反而越大。从图5(b)可以得到，当k2取值为原值时人体加速度最大，当k2的值大于或小于该值时人体加速度都会减小。从图5(c)中可以看到，c的取值对人体加速度几乎没有影响。

对以上时域响应量进行FFT变换可以得到Berg模型中k1、k2和c3个参数变化时对应的人体加速度功率谱密度曲线，如图6图所示。在图6(a)中，当k1取原值时人体的共振频率为1.12 Hz，加速度功率谱密度为0.37 m2/s3。当k1取1.5倍原值时，其共振频率减小为1.06 Hz，功率谱密度幅值较原值减小了29.3%。当k1取0.5倍原值时，其共振频率增大为1.19 Hz，功率谱密度幅值较原值增大了21.1%。可见k1的取值与人体加速度功率谱呈负相关。在图6(b)中，可以看到当k2的值大于或小于其原值时所对应的功率谱密度值都会减小，且在幅值处更为显著。在图6(c)中，3条曲线基本重合在一起，可见c的取值对于人体加速度功率谱密度的影响相对较小。

2.3 人体加权加速度均方根值的仿真分析

根据ISO2631标准规定[9]，对人体加速度时间历程a(t)进行频谱分析，得到功率谱密度函数Ga(f)；再根据式(6)即可计算出频率加权后的垂向加速度均方根awk

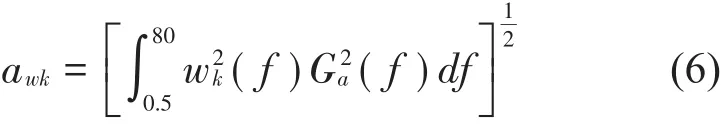
其中垂向频率加权函数

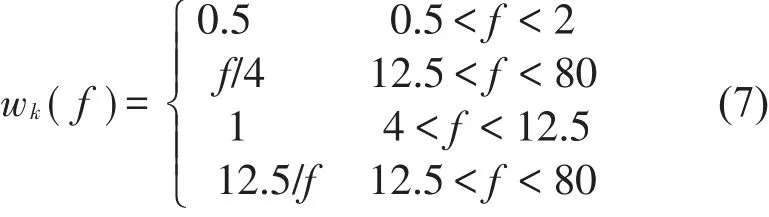
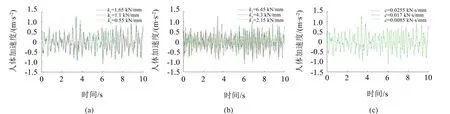
图5 不同Berg参数下的人体加速度

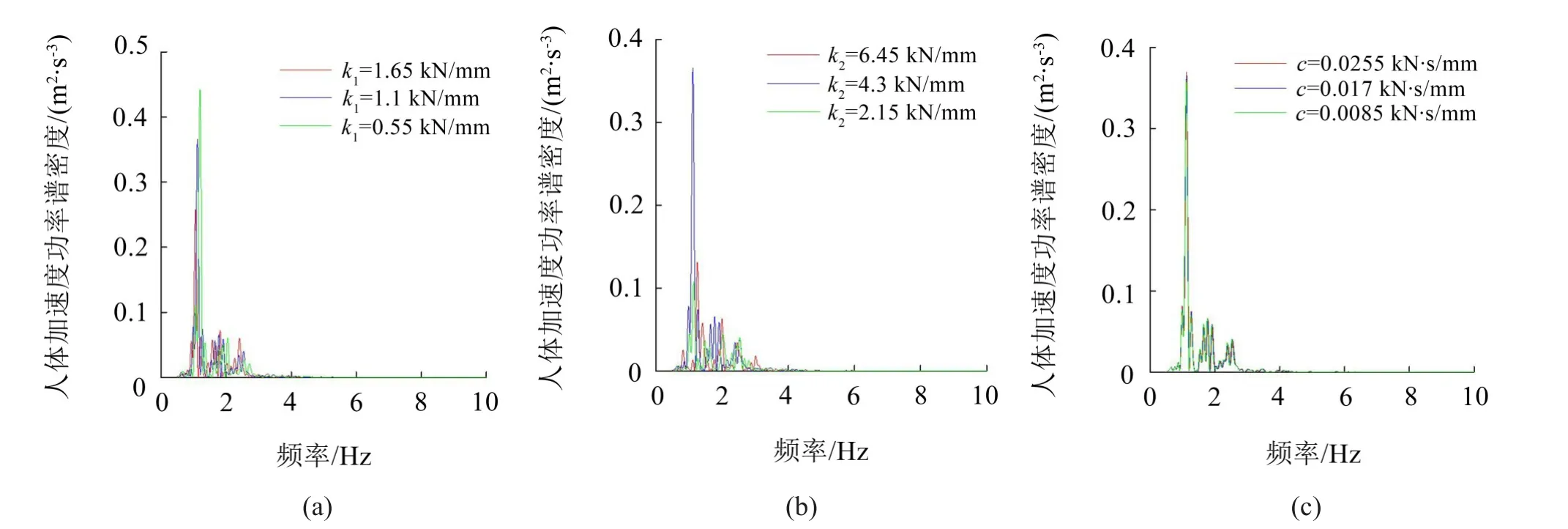
图6 不同Berg参数下的人体加速度功率谱密度

将所求得的值和加权加速度均方根值与人的主观感觉进行对比，即可分析出舒适程度。从图7(a)和图7(b)可以看出，随着座椅刚度和悬架刚度增大，其加权加速度均方根值也增大。相比未考虑橡胶衬套，在同一刚度下的加权加速度均方根值较前者减小0.018左右，并且两者的差值呈增大的趋势。从图7(c)和图7(d)可以看出，随着轮胎刚度和座椅阻尼值增大，其加权加速度均方根值不同程度减小，从图7(d)中可以看到座椅阻尼值对加权加速度均方根值的影响曲线比较平滑。同一座椅阻尼值下考虑橡胶衬套时的值比未考虑橡胶衬套时减小0.02左右，而随着轮胎刚度增大，考虑橡胶衬套时的加权加速度均方根值与未考虑橡胶衬套时的差值越来越大。从图7(e)可以得到，随着悬架阻尼增大，考虑橡胶衬套时和未考虑橡胶衬套时的变化趋势是不同的。未考虑橡胶衬套时，悬架阻尼和座椅阻尼的增大都使得加权加速度均方根值减小，而考虑橡胶衬套之后，随着悬架阻尼增大，加权加速度均方根值增大，并且增大的趋势很明显。从图7(e)可以明显看到由于考虑Berg摩擦特性致使加权加速度均方根值的变化曲线较为曲折。考虑橡胶衬套和未考虑橡胶衬套时，不同的汽车悬挂参数对人体加权加速度均方根值的影响趋势不完全相同，考虑橡胶衬套时也应注意不同悬挂参数给舒适性带来的影响，应该综合考虑以选择恰当的参数值。

2.4 Berg模型参数对awk的影响

图8是Berg模型中k1、k2和c从其原值0.5倍左右一直增大到其原值的1.5倍左右时人体加权加速度均方根值的变化曲线。在图8(a)中，随着k1增大，其对应的加权加速度均方根值逐渐减小。由图8(b)可以得到，随着k2增大，其加权加速度均方根值先基本不变，后增大，再减小。从图8(c)中可以看到，随着c值增大，其所对应的加权加速度均方根值也逐渐增大。

3 结语

通过将Berg模型橡胶衬套加入车辆悬挂系统，建立含有Berg摩擦特性的车辆振动模型。根据拉格朗日方程得到系统的运动微分方程，以随机路面作为激励，得出一些系统振动响应量。从分析结果可知：

(1)在时域上，由于考虑了碳黑增强剂的摩擦效应，Berg模型对人体加速度和悬架动挠度起到了减小作用，尤其在峰值处产生的效果更加明显；

(2)在频域上，在考虑橡胶衬套后其响应量的功率谱密度曲线都有所降低，尤其在幅值处比较显著，表明其有效地减弱了振动；

(3)Berg模型中k1与人体加速度功率谱呈负相关关系，k2为原参数值时功率谱密度最大，c对功率谱密度的影响很小；

(4)依据ISO2631-1:1997(E)，选取竖直方向加速度的加权值作为评价标准评价乘客的主观感受，结论为没有不舒适。考虑橡胶衬套后加权加速度均方根值较之前未考虑时的值在不同程度上都有所减小，并且随着座椅刚度和悬架刚度值增大，其加权加速度均方根值呈增大趋势。随着轮胎刚度和座椅阻尼值增大，其加权加速度均方根值呈减小趋势。对于悬架阻尼而言随着其值增大，未考虑橡胶衬套时呈负相关，而考虑橡胶衬套时呈正相关。

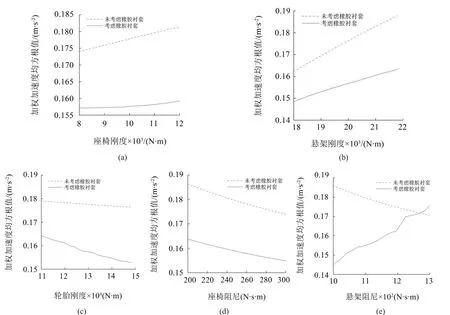
图7 悬挂参数对人体加权加速度均方根值的影响对比图

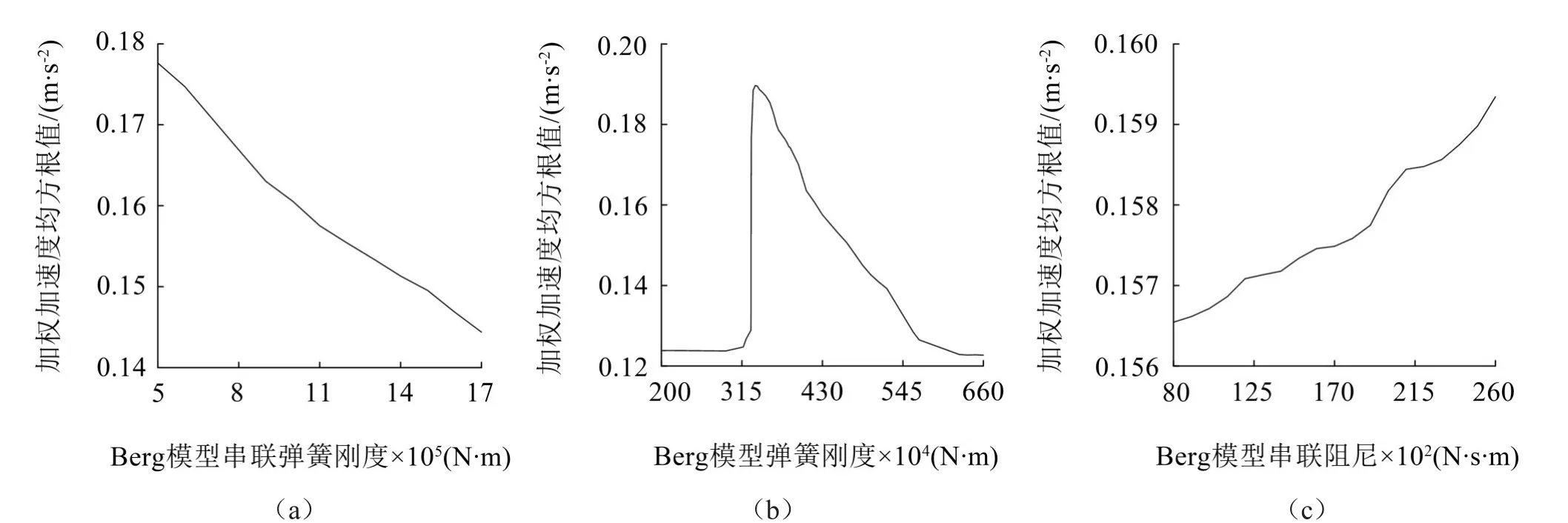
图8 Berg模型参数对人体加权加速度均方根值的影响图

（5）对于Berg模型参数而言，随着k1增大，加权加速度均方根值呈减小趋势，随着k2增大，加权加速度均方根值呈先基本不变，后增大，再减小趋势。随着c增大，加权加速度均方根值呈增大趋势。

综上可以得到，Berg模型的摩擦特性能够有效减弱车辆振动，提高汽车平顺性。分析时应综合考虑橡胶衬套和车辆悬挂系统参数对系统振动的影响，这可为提高汽车平顺性提供部分理论参考。