基于连续数值模拟的筒仓卸载过程中颗粒物压强及其速度场分析*

周益娴

(华北电力大学,非能动核能安全技术北京市重点实验室,北京 102206)

1 引 言

科学界通常认为颗粒介质(granular media)是大于100 μm的颗粒集合体[1],其布朗效应和颗粒物质之间的凝聚力相较于重力及碰撞力可以忽略.颗粒介质在自然界以及工业生产中广泛存在,因此对颗粒体系的深入研究将会对全球工业与经济的发展有极大助益[2].早期颗粒流的研究手段主要是实验和离散颗粒介质的数值模拟(DEM).离散元数值模拟方法主要是考虑每个个体颗粒物质之间的碰撞[3].该方法发展已较为成熟,但计算速度慢.近年来,法国颗粒物质研究组提出的局部本构理论[4]得到了广泛使用,这一局部流变理论使得将流体力学方法应用于颗粒流模拟成为可能,这极大程度地降低了运算时间.另外,该理论加深了人们对颗粒流内在物理机理的理解.该方法主要描述的是与固体态相差甚远的液体状态,其本质是将颗粒物质看成带有摩擦性质的非牛顿流体.之后Jop等[5]将此局部流变学从二维向量形式推广至三维张量形式.该理论被证实能够应用在许多密集颗粒流构型当中,例如颗粒物坍塌[6]、筒仓卸载[7,8]等.但是存在一定的局限性,第一个局限性是无法描述颗粒物开始流动和停止流动的现象,第二个局限性是无法描述堵塞状态的运动[9].

颗粒物在筒仓或沙漏中的流动是一个经典的颗粒介质基础研究现象.人们很早就发现沙漏比水漏作为计时器更加简便和准确.对于出口在底部的筒仓卸载问题已有大量的研究.当容器尺寸足够大时,颗粒物的流量始终保持恒定,并且只与出口尺寸有关,这是它的重要特征,但其原因和物理机理仍有待研究.普遍为人们所接受的解释是Janssen效应[10,11],即容器底部压强达到一定值后不再随颗粒高度增加而增加.这是由于颗粒与筒壁间存在着摩擦力,筒壁承担了部分颗粒重量.由于筒仓出口处的压强与颗粒物高度无关,因此流量也与高度无关.然而近来一些实验证明颗粒物的流量与出口处的压强不具有相关性[12,13].因此Janssen效应并不能完整地解释此现象.流量Q随孔径D变化的经验公式,早在60年代就由Beverloo 等[14]利用量纲分析和实验方法给出,并被大量文献证实相当精确可靠.近几年人们主要开展了筒仓倾斜情况下的研究[15−17],即出口方向与重力不平行,研究发现流量也保持恒定,并得到了与倾斜角度相关的流量经验公式.此外Zhou等[18]研究了出口位置在侧面(即与地面垂直,倾角为90°)的颗粒物卸载情况(实验所用筒仓如图1所示),该工作重点研究了容器厚度W和出口高度D对颗粒物流量的影响.该工作表明,出口在侧面的情况下,颗粒物流量仍旧保持恒定,并且作者发现了与出口在底部情况不同的流量规律.当D/W足够小时,流量规律与出口在底部时的情况一样,满足Beverloo经验公式,即流量为出口面积; 而当足够大时,流量规律则为可见,在容器厚度很小时,卸载流量呈现了与出口在底部情况下不同的规律.作者使用上述基于局部本构模型的连续模拟方法得到了与实验结果相同的流量规律,并且证明了导致该结果的主要原因是出口处流线的倾斜角受前后容器壁的摩擦力影响很大.可见,上述连续模拟方法能够较好地模拟筒仓卸载实验.本文将在已有工作的基础上,利用上述基于本构模型的连续数值模拟方法深入分析筒仓卸载现象.首先,分析距离出口近处压强和速度与W及D之间的关系.进而,由此研究压强与速度之间的关系,并利用上述数值模拟解释为何出口在底部时流量规律始终为

2 连续数值模拟

本文采用基于局部本构模型的连续数值模拟方法,即将颗粒物看成非牛顿流体,并且考虑颗粒物之间的摩擦力对颗粒流动的影响.非牛顿不可压缩的纳维-斯托克斯公式可以写为:

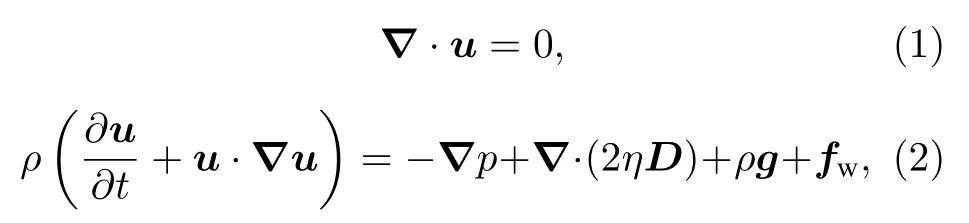
其中D是应变速率张量根据文献[5]中提出的理论,η为有效黏性系数,它与摩擦系数µ(I)以及局部压强p相关.D2为应变速率张量的第二不变量,

取流变学常数µs=0.4 ,∆µ=0.28和I0=0.4 ,但不考虑文献[5]提出的体积分数ϕ与I的关系式,此处取ϕ=1.方程(2)中fw代表前后两个壁面的总体摩擦力.本文实际采用的是二维模拟,为考虑容器前后壁对颗粒物的摩擦以及模拟三维效果,像赫尔-肖(Hele-Shaw)流动一样,将动量方程沿着y方向进行平均[19,20].根据颗粒流的特性,假设速度沿着y方向几乎保持不变,因此动量方程中的非线性项前的系数为 1.而黏滞力沿着y方向的积分之和则等于前后壁对颗粒物的摩擦力,假设该力为库仑力(在每个壁上值为−µwp).该力的方向应当与颗粒物运动方向相反,因此前后两个壁面的总体摩擦力大小为

取µw=0.1 ,通过改变容器宽度W的值来改变摩擦力的大小.可见本文中容器厚度W的影响等效于容器前后壁摩擦力大小的影响.本文利用上述类三维方法模拟图1所示实验,具体计算方法参见文献[18]和文献[21].在固体边界加上非滑移(noslip)的边界条件,在出口处压强设为零.数值模拟中容器及颗粒物的尺寸如表1所示(容器相关尺寸参数的定义见图1).

表1 容器及颗粒物的尺寸Table 1.Size of silo and particle.

3 模拟结果分析

3.1 出口在底部

可见在靠近出口处,动能项开始逐渐增大并且可以部分补偿压强降低,但由于摩擦力的存在,二者之间的关系并不满足伯努利方程.接下来重点分析距离出口较近处的颗粒物压强pp和速度vp与容器厚度W及出口高度D的关系.

3.1.1 压强结果分析

由前面分析可知,颗粒物在距离出口近处压强和速度变化明显,在远离出口的区域内压强变化较小,速度基本保持恒定,因此本文主要对距离出口近的区域进行分析.下面首先取该区域一个微元薄层进行受力分析.定义一个高度为∂λ的微元薄层区域(见图3中的蓝色虚线区域),且若取容器后壁面出口中点处为坐标原点,该区域坐标满足x∈[−D/2,D/2],y∈[0,W] ,z∈[λ,λ+∂λ].假设这个区域的边界处所受摩擦力与重力平衡,可得:

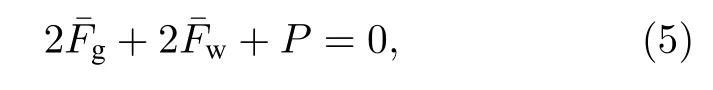
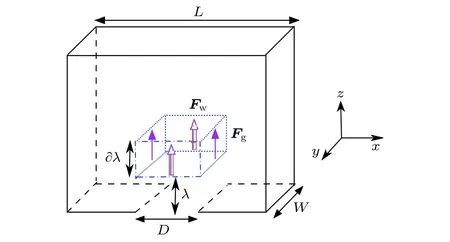
图3 出口在底部情况下容器内不同区域受力图Fig.3.Force diagram of different zones within the silo for the case with orifice at the bottom.

在y和z方向上积分,得到为

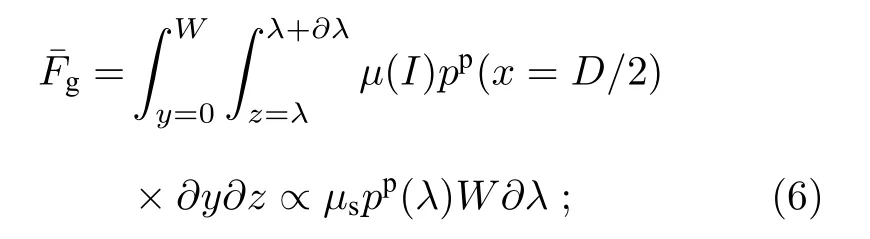
在x和z方向积分,可得为

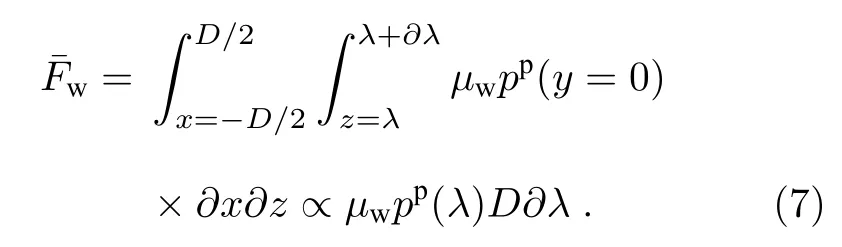
由于重量P=ρgD∂λW,取常数α1和α2,方程(5)可写成

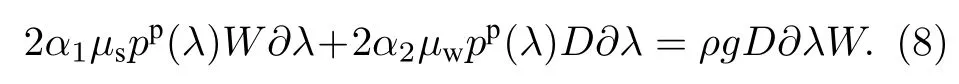
对颗粒物压强进行无量纲化操作，可得到：

其中γ1=1/(2α1µs),γ2=(α2µw)/(α1µs).(9)式表明颗粒物在靠近出口处压强仅仅与D/W相关.我们认为z=D处且位于容器中心线上的点也属于该区域,图4(a)显示了不同W值时z=D处无量纲化压强pp(D)/(ρgL)随D/L的变化曲线(模拟过程中容器宽度L始终不变).可见,当其他物理量不变时,D增大,出口处压强随之增大,这与方程(9)的增减性相符合.且随着W降低,压强与D的相关性逐渐降低.当其他物理量不变,W变化时,颗粒物压强与W强相关.显见当W降低,颗粒物在z=D处的压强降低,同样与方程(9)的增减性相符合.图4(b)显示无量纲化压强pp(D)/(ρgD)随D/W的变化曲线,模拟数据几乎重叠并落到一条曲线上,图中黑色虚线是利用最小二乘法将模拟结果与方程(9)拟合得到的,可见模拟结果与方程(9)符合良好.可得到如下关系:

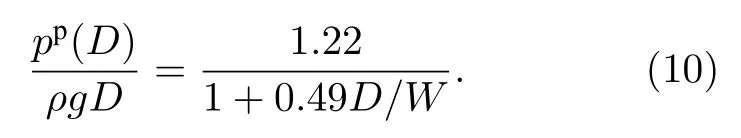
由方程(10)中γ2=0.49 可推出,当D/W≪2时,可得到pp(D)∝ρgD,压强仅与D相关; 而当D/W≫2时,可得到pp(D)∝ρgW,压强只与W相关.因此根据D/W的大小,压强呈现出两种截然不同的相关性.可见出口在底部情况下出口附近的压强与Zhou 等[18]得到的出口在侧面的颗粒物流量有相似的规律.

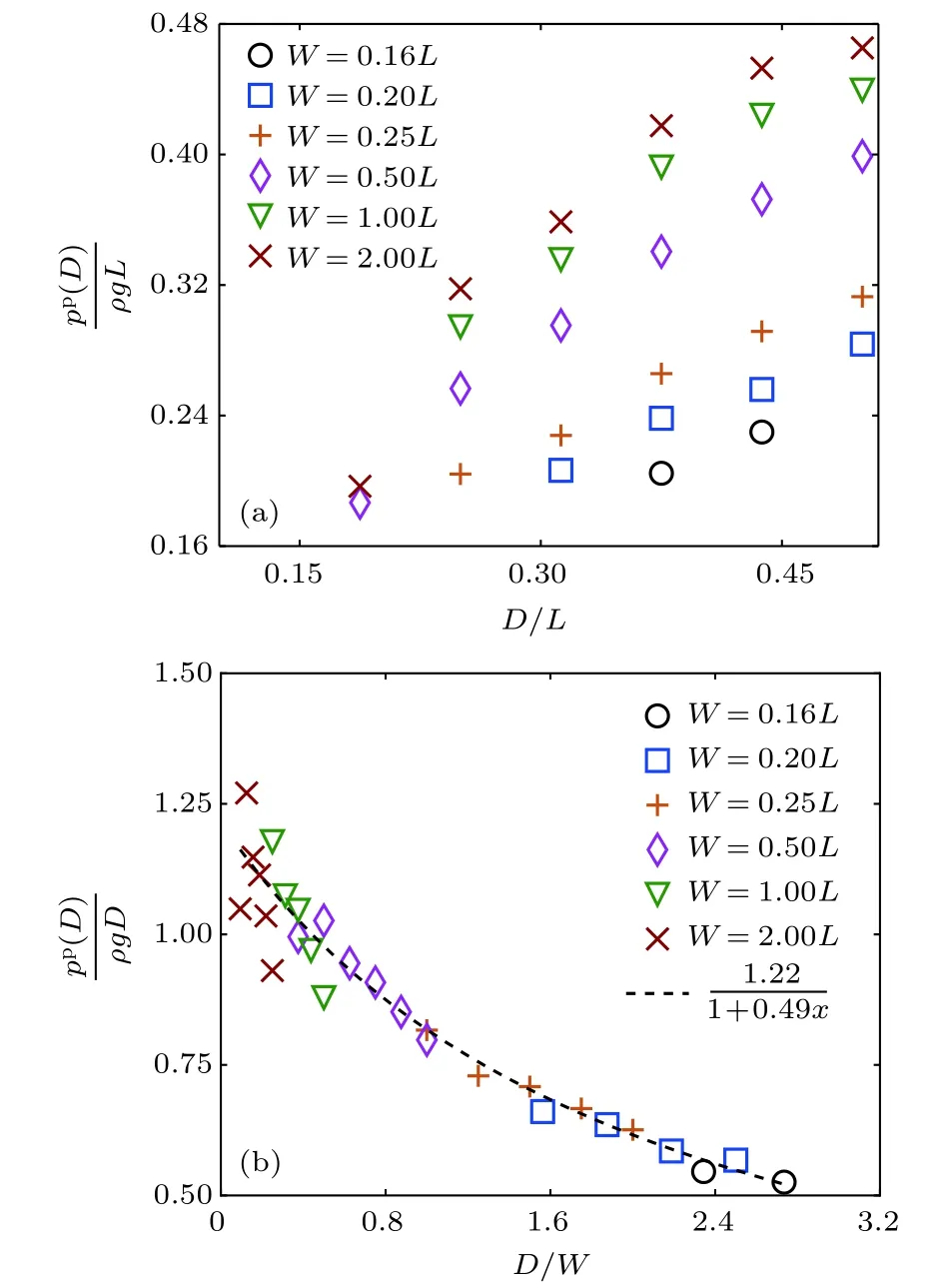
图4 在 W 不同的情况下距离出口 D 处的颗粒物压强pp(D)结果(a)无量纲化压强 pp(D)/(ρgL)随无量纲化出口尺寸 D/L 的变化;(b)无量纲化压强 pp(D)/(ρgD)随无量纲化出口尺寸 D/W 的变化Fig.4.Results of granular pressure at the distance D from the orifice pp(D)for various W :(a)Dimensionless pressure pp(D)/(ρgL)vs dimensionless orifice size D/L ;(b)dimensionless pressure pp(D)/(ρgD)vs dimensionless orifice size D/W.

3.1.2 出口速度结果分析

大量的实验表明[22,23],对于出口在底部的情况,流量始终满足Beverloo方程,可见出口处速度没有像压强一样与相关.文献[22,23]指出,颗粒物流量与出口中心处法向速度呈正相关,因此图5(a)给出了无量纲出口中心处法向速度(即竖直方向速度)随着D/L的变化曲线.由图5(a)可见,当D/L值较大时,速度随着W变化会发生轻微改变.图5(b)画出了无量纲化出口中心处竖直速度随无量纲化出口尺寸D/W的变化,图中黑色虚线为通过最小二乘法得到的方程,可推出出口中心处法向速度与容器厚度及出口尺寸满足如下关系:

由分母上D/W前√的系数为0.02可知,当D/W≫50时,可得到此时流量只与W相关; 而当D/W≪50 时,可得此时流量只与D相关,满足Beverloo定律.实际情况下,D/W≫50很难被满足,因此,在文献[22,23]中,出口在底部的矩形筒仓卸载问题仍旧满足Beverloo定理,没有出现流量与W相关的情况.

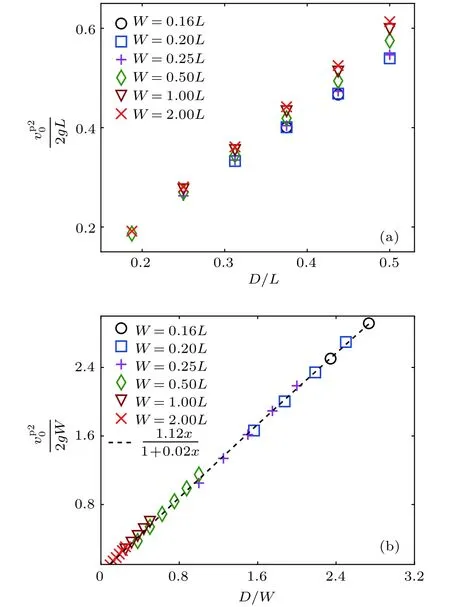
图5 在 W 不同的情况下位于出口处中心线的竖直方向速度 结果(a)无量纲化速度/(2gL)随无量纲化出口尺寸 D/L 的变化;(b)无量纲化速度/(2gW)随无量纲化出口尺寸 D/W 的变化Fig.5.Results of vertical velocity on the central streamline for various W :(a)Dimensionless vertical velocity /(2gL)vs dimensionless orifice size D/L ;(b)dimensionless vertical velocity /(2gW)vs dimensionless orifice size D/W.

3.2 出口在侧面

图6显示了出口在侧面的情况下流量恒定期间某一时刻压强、速度以及无量纲常数I的分布图.与出口在底部的情况非常相似,压强在出口处降低而速度显著增大,I的值在出口处最大,且最大值为 0.1 左右.接下来分析不同区域内的压强pp和速度vp值与容器厚度及出口尺寸的关系.

3.2.1 压强结果分析

如图7所示,研究沿着流线方向距离出口约为D的区域,可假设颗粒物几乎沿着竖直方向运动,且流动区域沿x方向的尺寸约为D,同出口在底部情况做相同的受力分析,可以得到沿中心流线方向距离出口D处的压强与D和W的关系为

其中γ1=1/(2α1µs),γ2=(α2µw)/(α1µs).图8(a)给出了在W不同的情况下距离出口D处的颗粒物无量纲化压强pp(D)/(ρgL)随无量纲化出口尺寸D/L的变化,与出口在底部时一样,当W降低,颗粒物在z=D处的压强显著降低.随着W降低,压强与D的相关性则逐渐减弱.图8(b)显示了无量纲化压强pp(D)/(ρgD)随无量纲化出口尺寸D/W的变化,图中黑色虚线是利用最小二乘法将模拟数据与方程(12)拟合得到的,所得系数与出口在底部的系数非常接近(见图4(b)),可见,出口处的压强大小对于出口的位置并不敏感.

3.2.2 出口速度结果分析

对于出口在侧面的情况,颗粒物流动方向会发生偏离,将出口处运动方向与竖直方向的夹角记为θ.图9(a)为无量纲化总速度随无量纲化出口尺寸D/L的变化,可以看出,出口处总速度大小几乎与W无关(u0表示出口处水平方向的速度,v0表示竖直方向的速度),且水平速度可被表示为一个与总速度U0以及出口处运动倾斜角相关的函数(θ=arctan(u0/v0)):

图9(b)显示了速度倾斜角 sinθ随无量纲化出口尺寸D/W的变化,图中黑色虚线为将模拟数据拟合如下方程所得到,可见 sin(θ)与W呈现如下相关性:

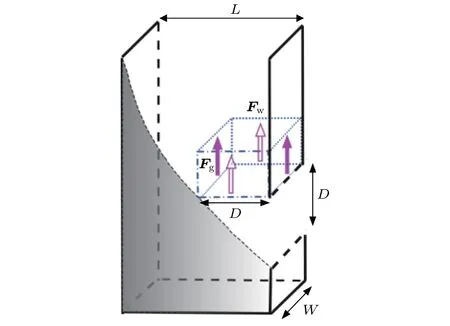
图7 出口在侧面情况下容器内不同区域受力图,图中阴影部分代表颗粒物停滞区域Fig.7.Force diagram of different zones within the silo for the case with lateral orifice,the dashed area represents the stagnant zone.

上述结果表明,出口处总速度大小只与D有关,但出口速度倾斜角θ与W相关,使得出口中心处法向速度(即水平速度u0)受到W影响,出现了新的流量规律.该现象可从N-S方程中得到解释,当W减小,摩擦力增大时,速度方向会与重力加速度方向更趋于一致[18].而由方程(14)中分母上D/W前的系数可知,当D/W≫4时,可得到 sin(θ)∝W/D,则出口中心处法向速度满足当D/W≪4时,可得到 sin(θ)为常数,则出口中心处法向速度满足可以推测,对于出口在底部的情况,出口处速度方向基本只与D相关,除非D/W≫50.由此可见,侧面开口情况下,出口中心处法向速度与W和D的两种相关性阶段的临界D/W值要远远小于出口在底部的情况.

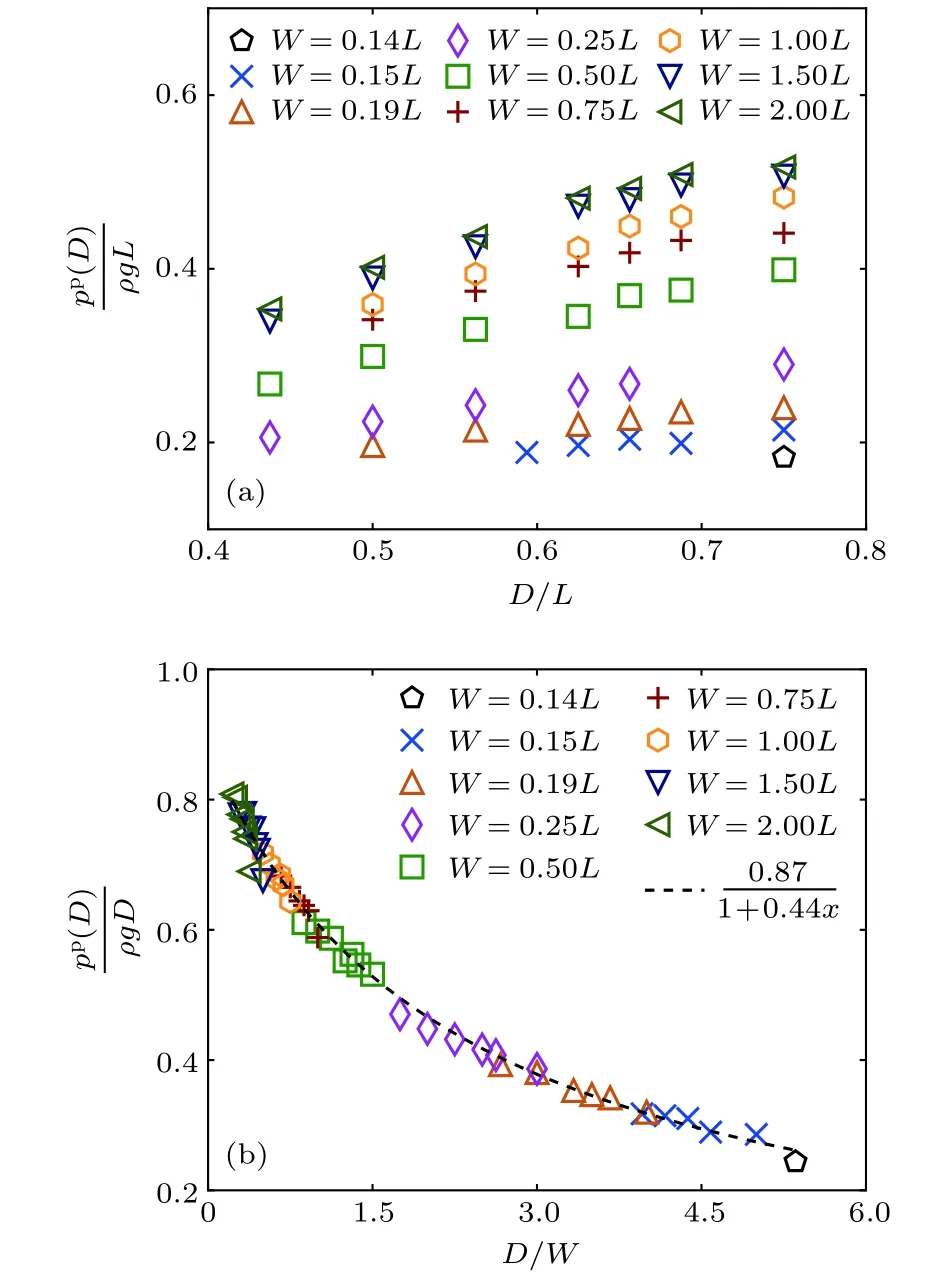
图8 在 W 不同的情况下距离出口 D 处的颗粒物压强pp(D)结果(a)无量纲化压强 pp(D)/(ρgL)随无量纲化出口尺寸 D/L 的变化;(b)无量纲化压强 pp(D)/(ρgD)随无量纲化出口尺寸 D/W 的变化Fig.8.Results of granular pressure at the distance D from the orifice pp(D)for various W :(a)Dimensionless pressure pp(D)/(ρgL)vs.dimensionless orifice size D/L ;(b)dimensionless pressure pp(D)/(ρgD)vs.dimensionless orifice size D/W.

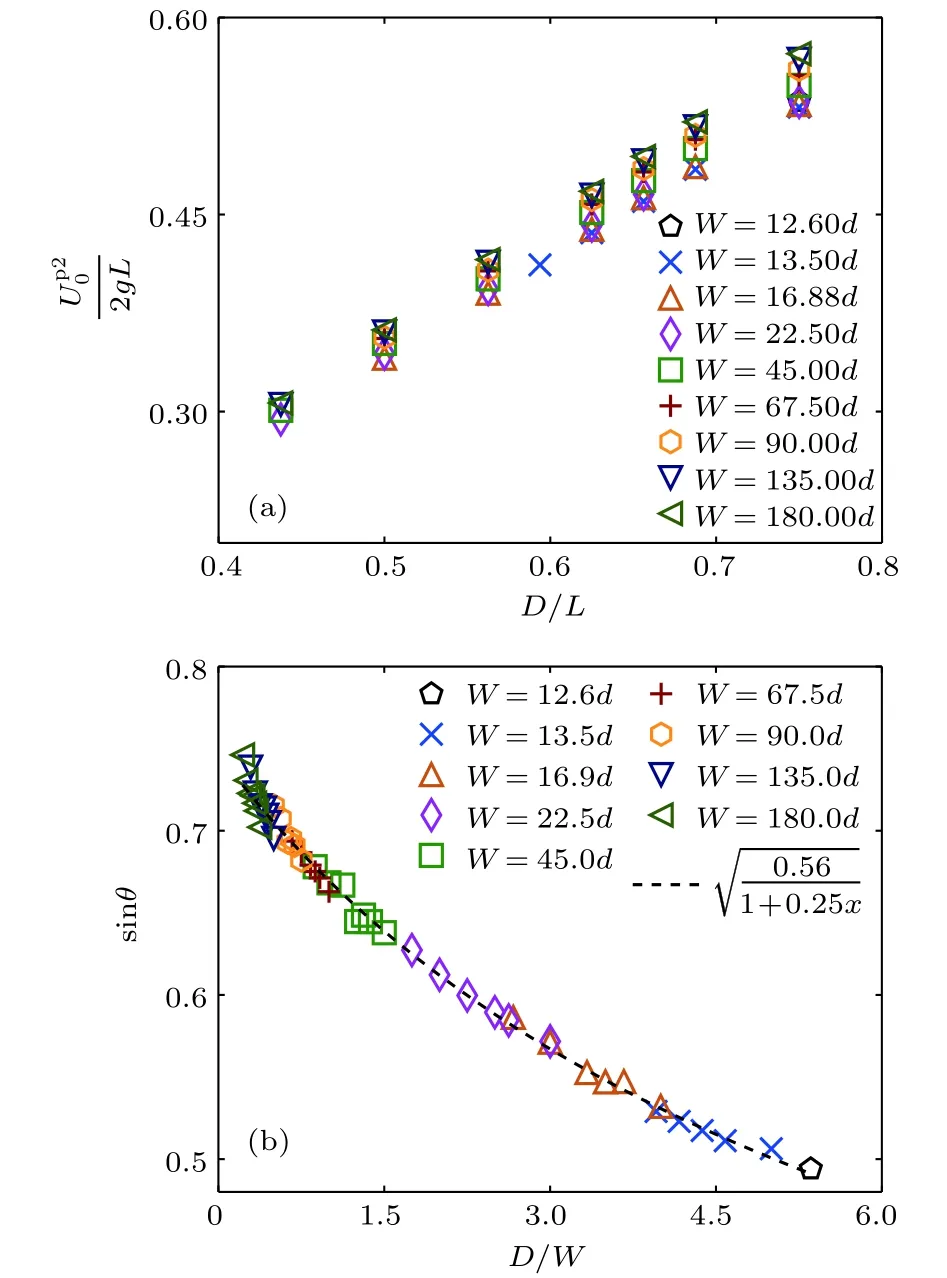
图9 在 W 不同的情况下位于出口处中心流线上速度结果(a)无量纲化总速度(2gL)随无量纲化出口尺寸D/L 的变化;(b)速度倾斜角 sinθ 随无量纲化出口尺寸D/W的变化Fig.9.Results of velocity on the central streamline at the orifice for various W :(a)Dimensionless total velocity /(2gL)vs dimensionless orifice size D/L ;(b)angle of inclination sinθ vs dimensionless orifice size D/W.

4 结 论

本文主要通过基于局部本构理论的连续数值模拟方法研究出口在底部和侧面的筒仓卸载问题.深入研究了容器厚度W(影响容器前后壁摩擦力大小)和出口尺寸D对颗粒物内部物理量的影响,着重分析了靠近出口处的压强及速度.首先通过受力分析预测了不同位置的压强与W以及D的关系,并利用模拟方法进行了验证.理论分析和数值模拟结果都表明,距离出口较近区域的压强存在两种相关性,当D/W足够小时,压强只与D相关,当D/W足够大时,压强只与W相关.出口在底部和侧面两种情况均呈现上述规律.随后,分析了出口处法向速度与W以及D的相关性,有趣的是,出口中心处法向速度呈现出与压强不同的相关性.对于出口在底部的情况,对于模拟中任意D/W值,出口中心处法向速度仍然只与D相关; 而出口在侧面时,当D/W足够小时,出口中心处法向速度只与D相关,当D/W足够大时,出口中心处法向速度只与W相关.这个结果与一直以来人们所认为的压强是影响出口速度的主要因素明显相违背[10],而与近来Perge等[12]以及Aguirre等[13]所做实验得出的结论一致,即筒仓出口处颗粒物流量与压强无关.对于出口在侧面的情况,总速度大小只与D相关,而出口中心处法向速度(水平速度)与W相关,其原因是出口处速度倾斜角与W相关,当W降低,出口处流线会更靠近竖直方向而总速度大小不变,因此出口中心处法向速度(即水平方向速度)降低.对于出口在底部的矩形筒仓卸载问题,本文还揭示了当容器厚度W与出口高度D相比很小时,流量仍然满足Beverloo定律的原因[22,23].这是由于与出口在侧面相比,出口在底部时,造成相关性规律改变的D/W临界值较大,只有当D/W≫50 时,出口流速(竖直方向速度)才会受W影响,呈现不同的变化规律,一般实际情况无法满足该条件.

综上所述,本文利用基于局部本构理论的连续数值模拟得到了与文献中实验一致的结果[18,22,23],并深入剖析了颗粒物内部运动机制,可见该模拟方法能够较好地预测颗粒流运动规律.从前文分析中可看出,停滞区的角度对流量影响较大,而Kamrin和Koval[24]所提出的非局部理论能够更好地描述该区域的运动情况,未来可将局部本构模型修正为更为精确的非局部本构模型,并比较二者在筒仓卸载问题中结果的区别.