具有时空时滞的反应扩散方程行波解的稳定性
闫瑞,王静玉
(山西财经大学 应用数学学院,山西 太原 030006)
0 引言
反应扩散方程通常用来描述和模拟人口动力学、化学、生物学等方面的实际问题。例如, 具有时空或非局部时滞的反应扩散方程通常用来描述物理和生物演化过程,见文[1-2]及其相关文献。本文研究如下具有时空时滞的反应扩散方程
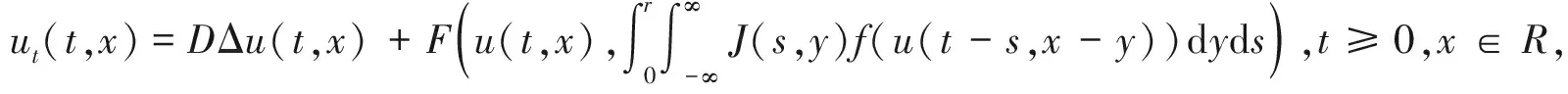
(1)
带有初值
u(s,x)=u0(s,x),s∈[-r,0],x∈R,
(2)
其中D>0是扩散系数,J是一个非负连续的核函数。对于方程(1),给出如下假设:
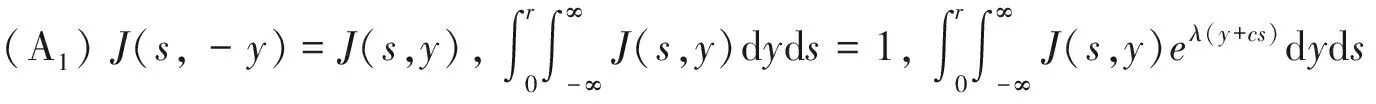
(A2)存在M>0,K∈(0,M)使得f∈C1([0,K],R),f(0)=0,f′(x)≥0,|f(x)-f(y)|≤f′(0)|x-y|,x,y∈[0,K].
(A3)F∈C2([0,K]×[0,f(K)],R),F(0,f(0))=F(K,f(K))=0,对x∈(0,K),F(x,f(x))>0,对于x∈(K,M),F(x,f(x))<0.另外,对于(x,y)∈[0,M]×[0,T],∂2F(x,y)>0,∂ijF(x,y)≤0(i,j=1,2),其中,T=maxx∈[0,M]f(x),∂1F(x,y)=∂F(x,y)/∂x,∂2F(x,y)=∂F(x,y)/∂y.
(A4)存在η∈(0,1)使得对任意α∈(1-η,1),F(x,αf(x))=0有唯一解ω>0,且对任意x∈(0,ω),F(x,αf(x))>0,且对任意x∈(ω,M),F(x,αf(x))<0.
(A5)∂1F(K,f(K))+∂2F(K,f(K))f′(0)<0.
由(A3)知方程(1)有两个常数平衡点0和K。我们主要研究连接0和K的行波解。本文中,(1)的行波解指的是φ,c满足如下的常微分方程
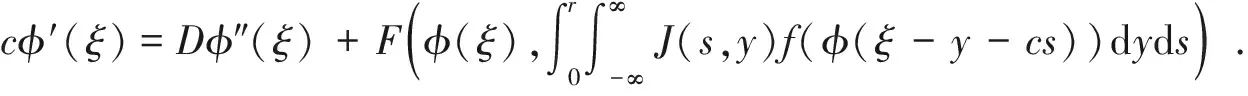
(3)
当φ单调时,称其为波前解。
方程(1)是一个具有双重非线性项的反应扩散方程。 函数f(x)可以看作是一种非线性的功能反应项, 例如, 非线性生育函数或非线性响应函数。Tian和Weng在文 [3]中利用有限时滞近似方法结合单调半流定理讨论了方程(1)的行波解的存在性。Xu和Xiao在文 [4] 中利用比较定理和Schauder不动点定理得到了当c≥c*(c*是临界波速)时行波解的存在性。可是, 并没有关于行波解的稳定性的相关结论。
近年来, 反应扩散方程行波解的稳定性受到了广泛关注。在这个问题上有很多结论。但时滞方程的稳定性的相关结论较少。Schaaf在文[5]中第一次运用谱分析方法得到了Fisher-Kpp方程行波解的局部稳定性。随后,Smith 和 Zhao 在文 [6]中利用挤压技术得到了具有双稳态非线性项方程的行波解的全局指数稳定性。紧接着, Mei等在文[7] 中利用加权能量估计的方法和比较原则得到了非局部Nicholson非线性方程行波解的全局指数稳定性。利用同样的方法, Yang 和Liu 在文[8]中得到了具有时空时滞的Nicholson果蝇模型的行波解的全局指数稳定。最近,Chern等在文[9]中研究了非单调的临界波速的稳定性,关于一些系统的行波解的稳定性和离散方程的行波解的稳定性都有相关研究,例如文[10-13]。 受上述文章的启发, 利用类似的方法, 我们研究了方程(1)的行波解的稳定性。
1 预备知识和主要结果
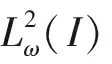
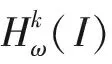
令T为一个正常数,B是一个Banach空间。C([0,T],B)表示由[0,T]上的B值连续函数构成的空间。L2([0,T],B)表示由[0,T]上的B值L2函数构成的空间。[0,∞)上的空间可以类似地给出。
定理1[8]假设条件 (A1)-(A4)成立, 则存在最小波速c*>0及相应的常数λ*(c*)满足
其中
对任意c≥c*, 方程(1)存在单调的行波解φ(x+ct)使得φ(-∞)=0,φ(+∞)=K,但当0
对任意c≥c*, 定义加权函数为
ω(x)=e-2λ*x,
其中λ*为定理1中定义的正常数。显然,当x→-∞时,ω(x)→∞,当x→∞时,ω(x)→0.
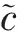
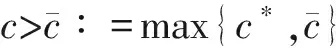
0=u-≤u0(s,x)≤u+=K, (s,x)∈[-r,0]×R,
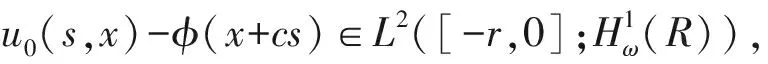
0=u-≤u(t,x)≤u+=K, (t,x)∈[0,+∞)×R,
且存在正常数μ使得
特别地,解u(t,x)指数收敛到φ(x+ct):
2 稳定性的证明
为了证明稳定性的结论,我们需要引入两个引理,见文[14-16]。
引理1 假设(A1)-(A4)成立, 若初始条件满足
0=u-≤u0(s,x)≤u+=K, (s,x)∈[-r,0]×R,
那么Cauchy问题(1)和(2)存在唯一的解u(t,x)满足
0=u-≤u(t,x)≤u+=K, (t,x)∈[0,+∞)×R.
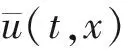
则
若给定的初值0=u-≤u0(s,x)≤u+=K, (s,x)∈[-r,0]×R,令

(4)
则
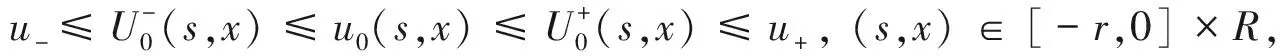
(5)
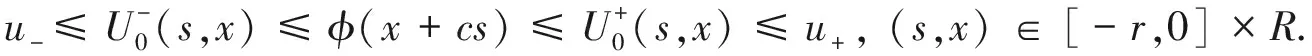
(6)
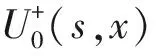
因此,由比较原则有
u-≤U-(t,x)≤u(t,x)≤U+(t,x)≤u+, (t,x)∈[0,+∞)×R,
(7)
u-≤U-(t,x)≤φ(x+ct)≤U+(t,x)≤u+, (t,x)∈[0,+∞)×R.
(8)
定理2的证明过程需要分三步。
首先,证明U+(t,x)收敛到φ(x+ct).
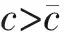
vt(t,ξ)+cvξ(t,ξ)-Dvξξ(t,ξ)-∂1F(ξ)v(t,ξ)=

(9)
带有初值v(s,ξ)=v0(s,ξ),(s,ξ)∈[-r,0]×R,其中
在方程(9)的两端同乘ω(ξ)v(t,ξ)e2μt,其中μ>0是一个正常数,得到

(10)
结合(10), 有
对上述不等式, 在R×[0,t]上分别对ξ和t积分, 得到

(11)
由于
其中η>0 .由Fubini定理及变量代换ξ-y-cτ→ξ,s-τ→s,y→y,τ→τ,得到
然后得到

(12)
对于非线性项Q,运用Taylor公式, 并结合(A2)和(A3)可得
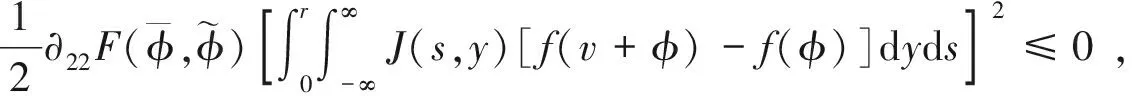
(13)
(14)
其中

(15)
为了得到估计,通过选择η与μ可以证明Bη,μ,ω(ξ)>0。于是得到如下结论。
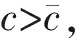
Aη,ω(ξ)≥C1>0,ξ∈R.
(16)
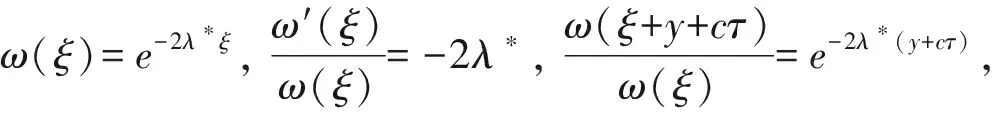
Aη,ω(ξ)≥2cλ*-2D(λ*)2-2∂1F(0,0)-η∂2F(0,0)f′(0)-
证毕。
引理4 令μ1>0是如下方程的唯一根
令μ<μ1,则
Bη,μ,ω(ξ)>0,ξ∈R.
(17)
证明由引理3可得
证毕。
将(15)与(17)代入(14), 得到如下估计。
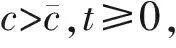
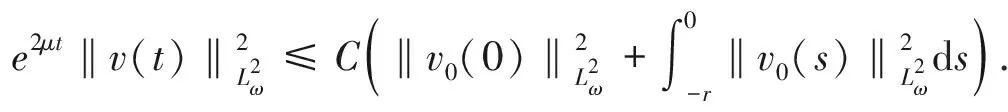
(18)
类似地,在方程(9)两端对ξ求导, 对得到的方程两端同乘以e2μtω(ξ)vξ(t,ξ), 然后在R×[0,t]上分别对ξ和t积分, 由(18)式可以得到如下的估计。
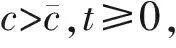
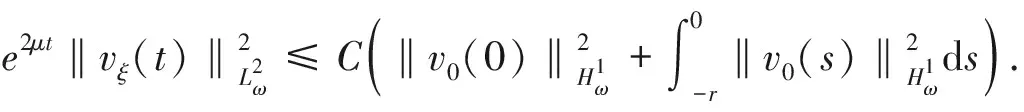
(19)
结合(18)和(19), 得到如下不等式。
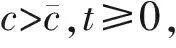

(20)
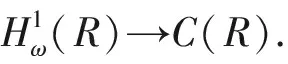
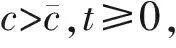

(21)
我们需要给出整个区间(-∞,+∞)上的估计, 因此, 需给出如下在ξ=+∞处的收敛性。
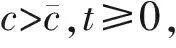

证明由于Q≤0, 由(9)可得
vt(t,ξ)+cvξ(t,ξ)-Dvξξ(t,ξ)-∂1F(ξ)v(t,ξ)
又
及
令ξ→+∞,上述不等式变为
上述不等式两端同乘以eμ2t,并在[0,t]上积分,得到

由上面两式得到

即

其中
由于(A5), 选择μ2>0使得
则v(t,∞)≤Ce-μ2t.证毕。
由引理8和引理9可直接得到下面结论。
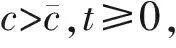
其中0<μ 其次,证明U-(t,x)收敛到φ(x+ct). 令 类似可得 其中0<μ 最后,证明u(t,x)收敛到φ(x+ct). 考虑如下传染病模型 (22) 其中b>a>0,u(t,x)为感染者在时刻t和位置x处的密度,a是受感染者的治愈率,b为接触率。 显然,方程(22)有两个常数平衡点u-≡0和u+≡1-a/b>0。 在文[17]中,作者已证明存在c*使得当c>c*时连接u-和u+的行波解是存在的。 注:当b>a时,随着时间的变化传染病个体的密度趋向于地方性水平。另外,当a↑b时,传染病个体的密度趋向于0。即当受感染个体的恢复率接近宿主接触率时,这种疾病将最终消灭。这表明,降低宿主-媒介接触率是控制疫情的有效途径。因此,研究结果将有助于预测传染病的发展趋势,识别传染病传播的关键因素,并寻求预防和控制传染病传播的最佳策略。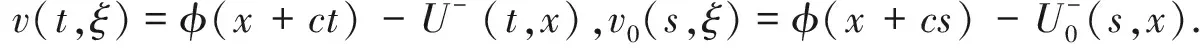
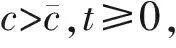
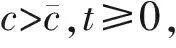
3 应用