平板自由下落的数值模拟

蔡琛芳,梁 彬

(中国航天空气动力技术研究院,北京 100074)

0 引 言

自然界中树叶和某些植物种子的飘落，扑克牌、纸片等轻质平板的掉落，以及水下气泡上升等常见现象，都会呈现规律、美丽的运动轨迹。这些有趣的现象看似简单，却包含了复杂的流体力学和动力学机理，近年来引起了人们更多的关注和研究[1-11]。Belmont等[1]在三种不同流体中进行了纸片自由下落实验，确定了纸片自由下落中摆动和翻滚两种运动轨迹互相转变的临界弗劳德数Fr。Wang等[2-3]对二维平板的下落问题进行了实验和计算研究，建立了相应的力学模型，解释了其非定常气动力机制。Wan等[4]、Tian和Shu[5-6]、Kumota和Mochizuki[7]分别采用实验和数值模拟方法研究了平板自由下落中的流动涡结构和发展过程，并分析了其中的致力机理。Hu和Wang[8]在动力学系统方程的基础上，引入微分方程分支理论，分析了平板自由下落的稳定性问题。Zhong等[9-10]还使用立体视觉的方法，首次研究了三维、六自由度圆盘的自由下落，并引入了螺旋运动和平动两种运动形式。这些研究结果表明，空气中纸片或树叶自由下落的雷诺数为1000左右，与较大昆虫飞行的雷诺数相似[12]。研究平板自由下落问题，对树叶和种子的飘落、昆虫飞行等自然现象，以及仿生微型飞行器等工程应用的相关物理问题中的流体力学和动力学研究具有一定的指导意义。

综上所述，以往的研究主要以实验手段为主，并且均采用匀质平板作为研究对象。本文在上述研究的基础上，针对轻质平板自由下落的简化模型——二维平板自由下落这一经典问题，进一步探讨转动惯量、初始角度和非匀质平板质心位置对下落运动的影响，采用耦合求解N-S方程和运动方程的方法数值模拟进行系统的研究，并分析其中的流体力学和动力学机制。

1 方 法

1.1 控制方程

平板自由下落过程中，受到气动力和重力的共同作用，其运动受N-S方程和运动方程共同支配，两者共同构成控制方程。

在二维惯性坐标系Oxy下，非定常不可压N-S方程的无量纲形式为：

(1)

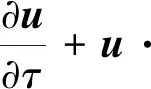
(2)

式中，u是无量纲速度，p是无量纲压力，τ是无量纲时间，是梯度，2是拉普拉斯算子，Re是雷诺数。

二维平板在惯性坐标系下的运动方程如下：

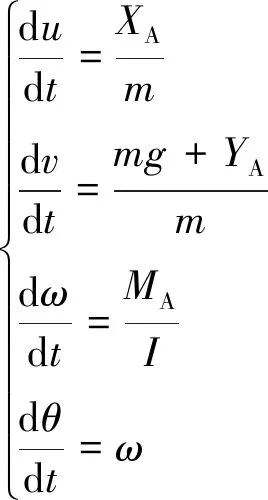
(3)

式中，u、v分别是平板在x轴(水平方向)和y轴(垂直方向)上的运动速度；ω和θ是平板转动速度和转动角度；XA、YA和MA分别是x轴、y轴上的气动力分量和气动力矩；m是平板质量；I是平板转动惯量；g是重力加速度。

1.2 计算方法

N-S方程的数值求解方法与文献[13]中的方法相同，采用拟压缩性算法求解[14-15]。算法和离散方法本文不再赘述。其中在求解动量方程时，引入了虚拟时间步来保证速度散度为0的不可压条件。计算时采用刚性动网格技术，网格为贴体正交结构，计算过程中网格随平板刚性运动。所用网格密度为60×49(径向×周向)，时间步长Δτ=0.0005。

运动方程中需要通过求解N-S方程获取气动力和力矩项，而N-S方程中也需要通过求解运动方程获取边界条件，因此求解二维平板的自由下落时必须对两者进行耦合求解。这里采用了 “弱耦合”求解[16]的方法，具体步骤如下：

1)假设已知平板tn时刻的状态变量Λn=(un,vn,ωn,θn)，因此确定N-S方程的边界条件，通过前文的求解方法数值求解N-S方程得到tn时刻的流场和气动力、气动力矩等信息；

2)采用预估校正欧拉法推进求解运动方程。首先用欧拉法估计tn+1时刻状态变量的值(上标*表示估计值，f表示方程组(3)的右端函数)：

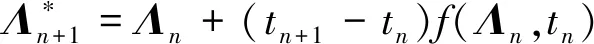
(4)

3)修正tn+1时刻状态变量的值，即tn+1时刻最终值：

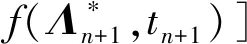
(5)

4)根据解出的tn+1时刻的平板状态变量，重复第1步的步骤。如此反复，推进求解。

综上，可实现运动方程和N-S方程的耦合求解。

1.3 无量纲方法

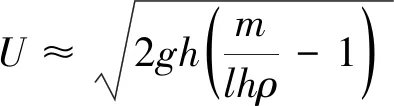
2 数值模拟结果

结合之前的研究成果，本文选择宽厚比β=14、无量纲质量m+=0.3857的平板在水中的下落作为研究对象，取ρ=1.0 g/cm3，υ=0.0089 cm2/s。根据估算的平均下落速度，Re=2094。

2.1 实验结果的模拟

首先采用实验结果对数值模拟方法进行验证。图1和表1给出了二维平板自由下落轨迹的数值模拟结果和实验结果。其中实验结果来源于Anderson等[2]使用拟二维平板在水槽中的实验：H=0.081 cm、β=14、I=0.026 g·cm2、Re=1147。数值模拟中采用了相应的无量纲参数。

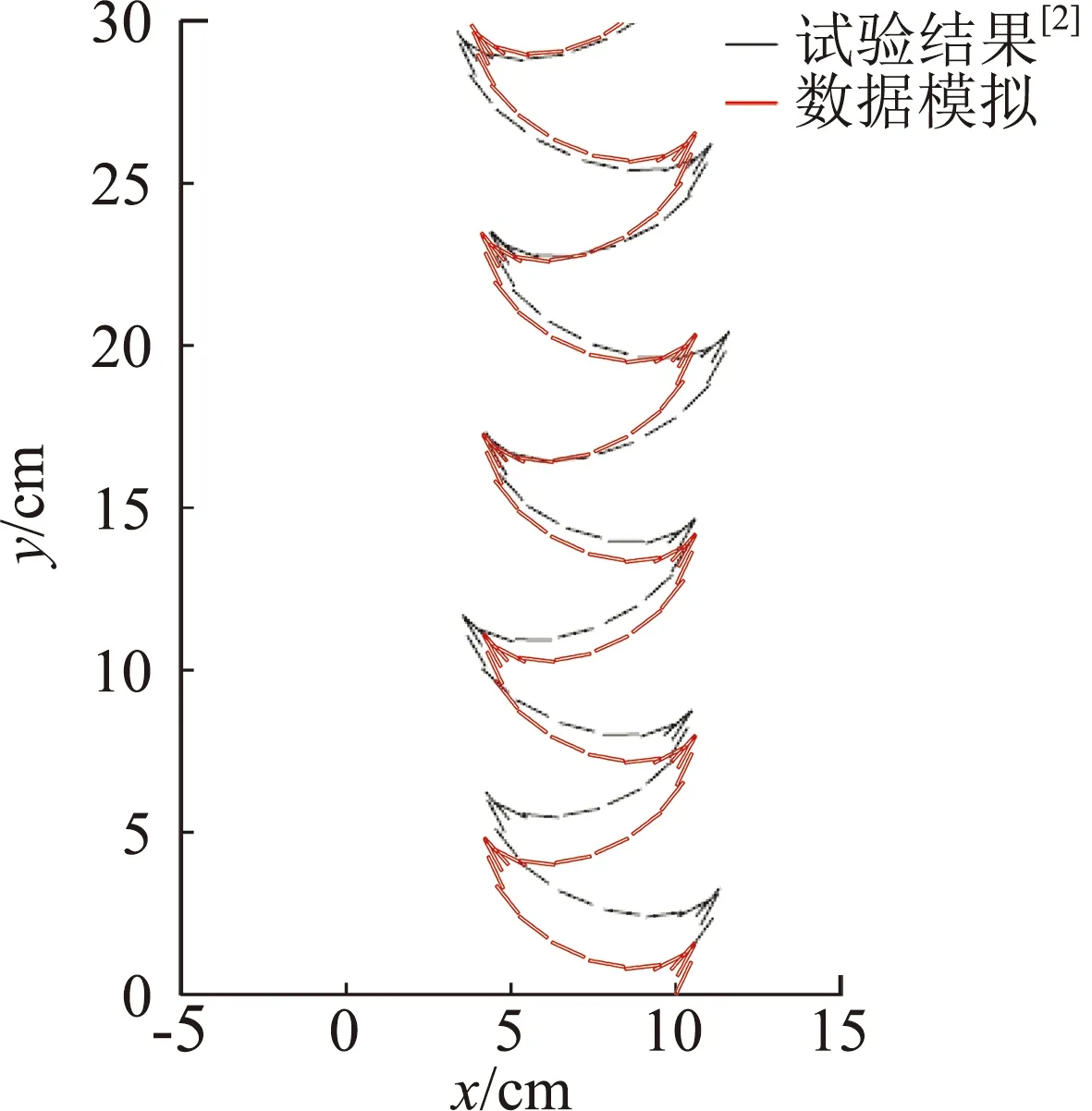
图1 摆动运动下落轨迹Fig.1 Trajectories of fluttering

表1 摆动运动平均速度Table 1 Average velocities of fluttering

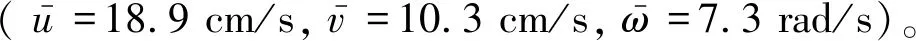
同时，为了研究平板初始角度对下落运动的影响，分别选取初始角度0°、45°、90°和135°进行了计算。根据数值模拟结果，其他参数不变的情况下，不同初始角度平板进入稳定下落运动的时间长短不一，但并不影响其稳定后的运动。在后面的数值模拟当中，都采用了更快进入稳定、规律的下落运动状态的初始角度(一般为45°或135°)。

2.2 转动惯量的影响

为研究转动惯量对平板下落运动的影响，在其他参数不变情况下，对无量纲转动惯量I+=0.001～5的平板进行了数值模拟。图2和图3分别显示了几个典型状态下落过程运动轨迹和无量纲速度变化曲线。

数值模拟结果显示，无量纲转动惯量I+≈0.95是下落运动转变的临界点。当平板转动惯量较小(I+<0.95，图2a、图2b时，下落运动呈现规律的摆动现象。随着转动惯量的增大,摆动的频率减小、周期增大。当平板转动惯量较大(I+>0.95，图2c)时，下落运动转变为规律的翻滚，转动惯量变化对其运动影响并不明显。

(a)高频摆动 (b)低频摆动 (c)翻滚图2 平板自由下落运动轨迹Fig.2 Trajectories of freely falling plates

(a)高频摆动

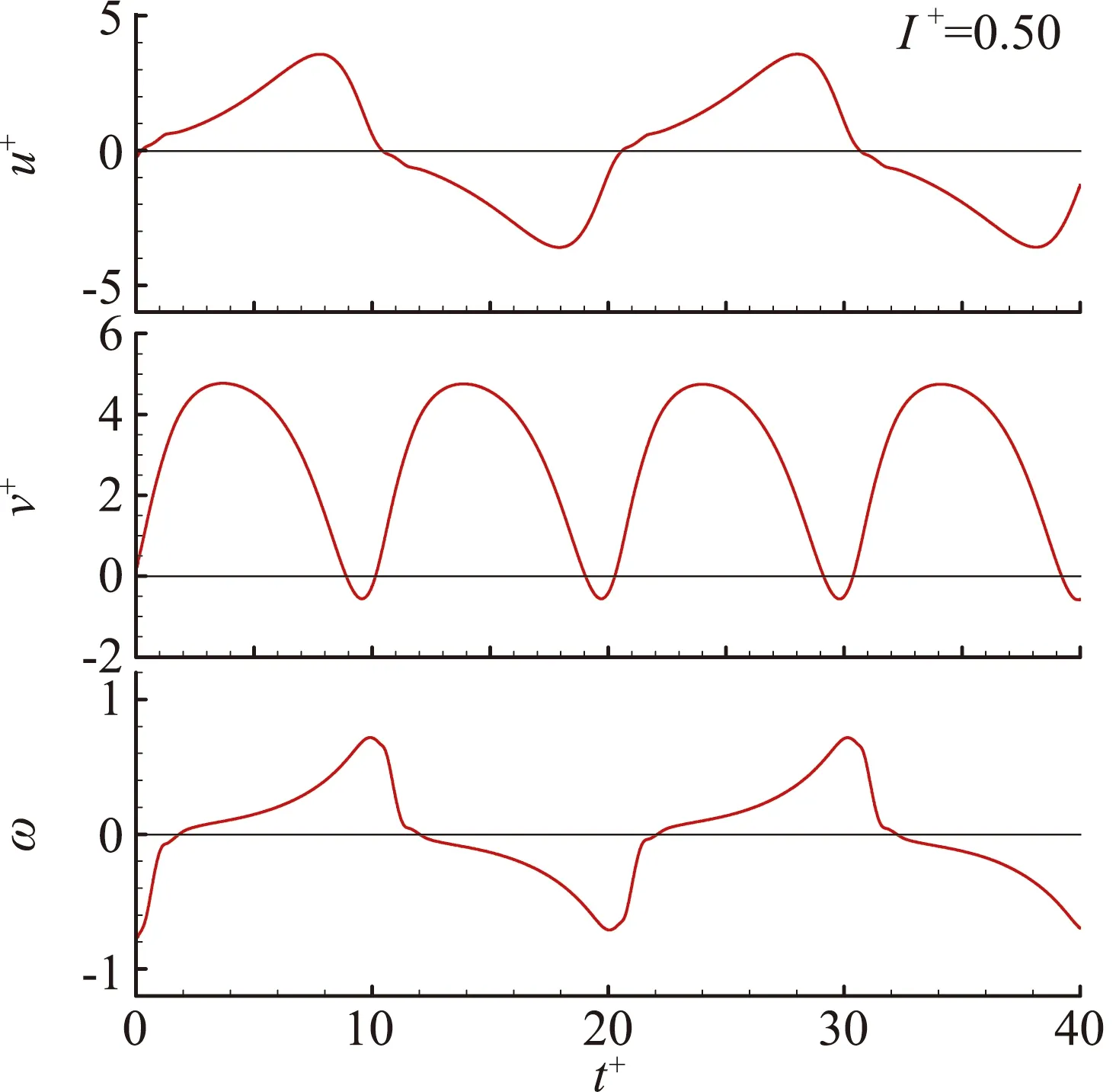
(b)低频摆动

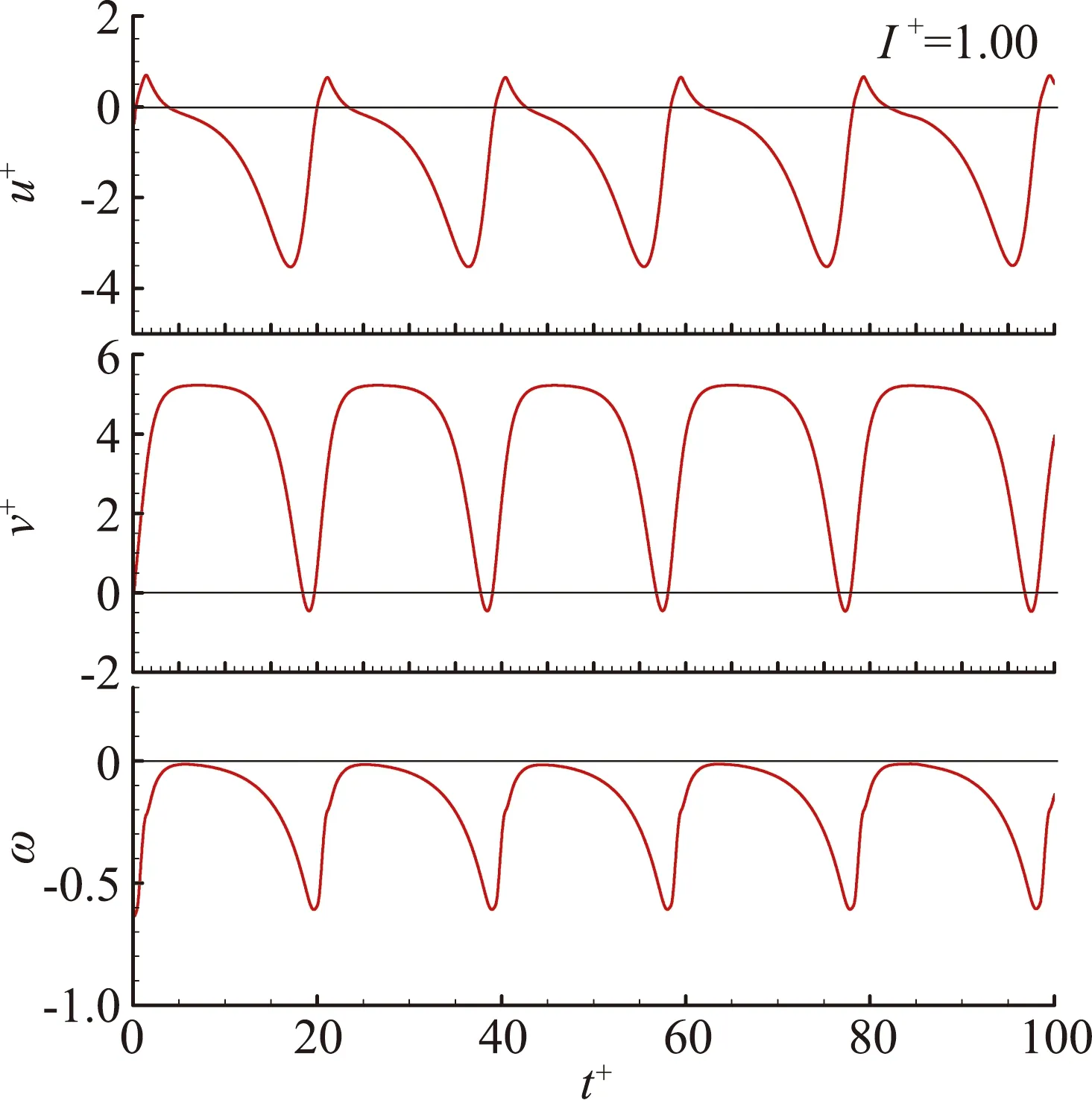
(c)翻滚图3 无量纲速度变化曲线Fig.3 Dimensionless velocities

图2和图3显示，两种运动都呈现了周期性的速度和位移变化，但区别在于摆动运动的速度和位移变化是对称的，而翻滚运动在水平方向和角度方向上体现了单侧的偏向性。两种运动的特点在水平速度和垂直速度u+-v+曲线(图4)中得到明显体现：摆动运动为“∞”形轨迹，且周期越长“∞”形轨迹越大；翻滚运动则呈单侧的“O”形轨迹。

2.3 质心的影响

前文的研究当中，认为二维平板为匀质，即质心位于平板中点。这里首先选取I+=0.0323的摆动下落状态，对非匀质,即不同的质心位置(设质心与平板中点距离为l，l=0～0.25L),平板进行了数值模拟研究，如图5和图6所示。

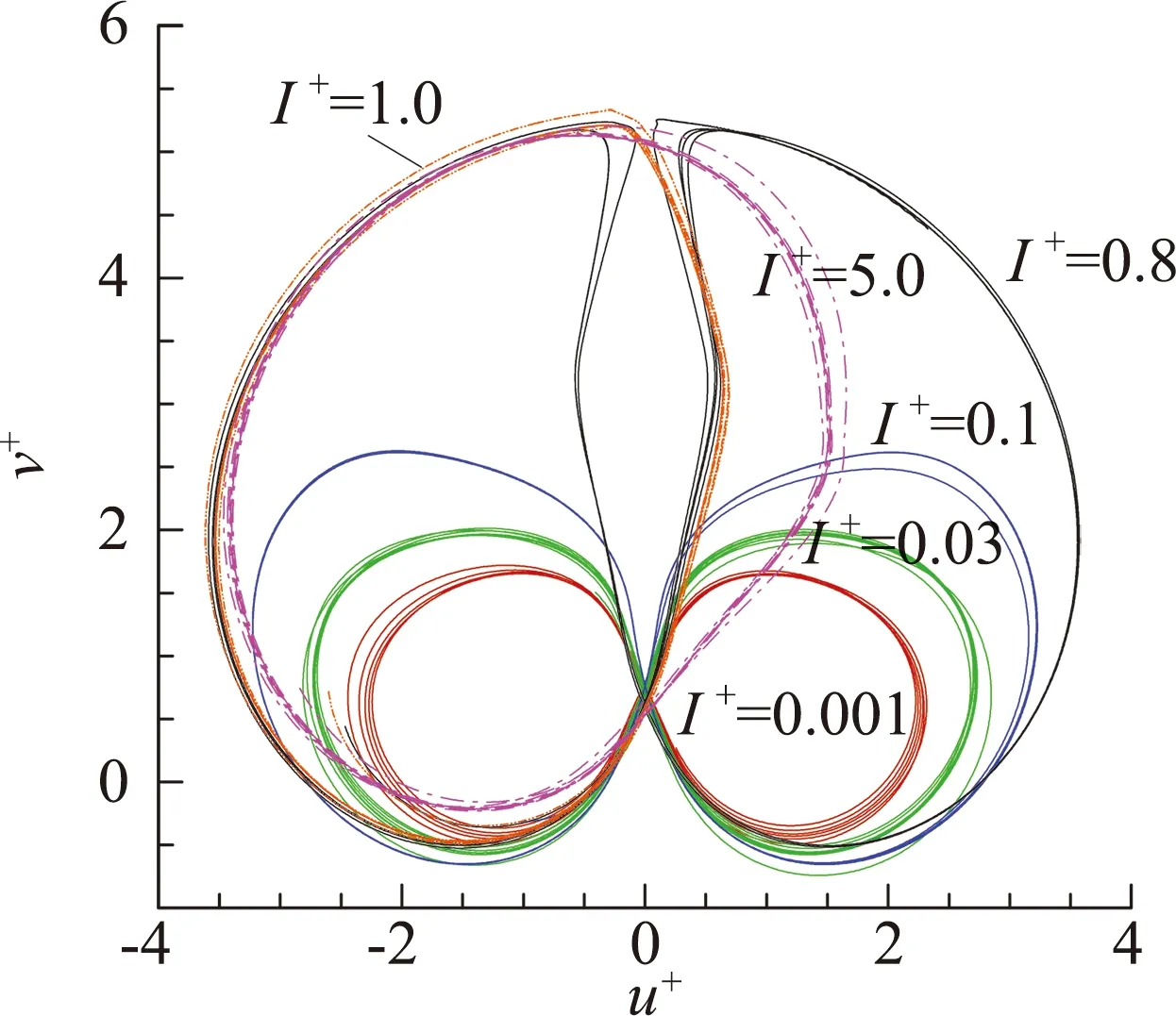
图4 无量纲速度u+-v+曲线Fig.4 u+ versus v+

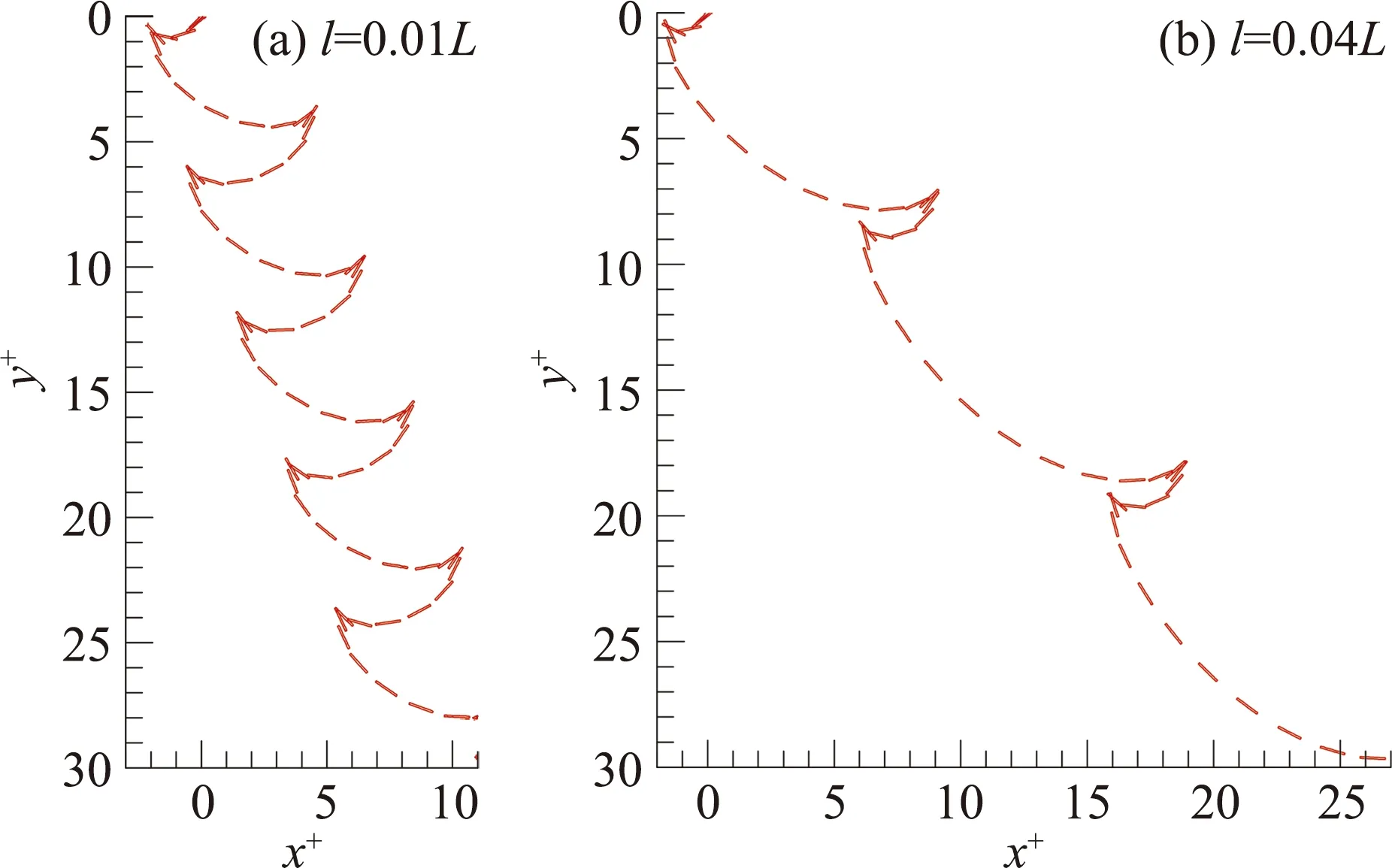
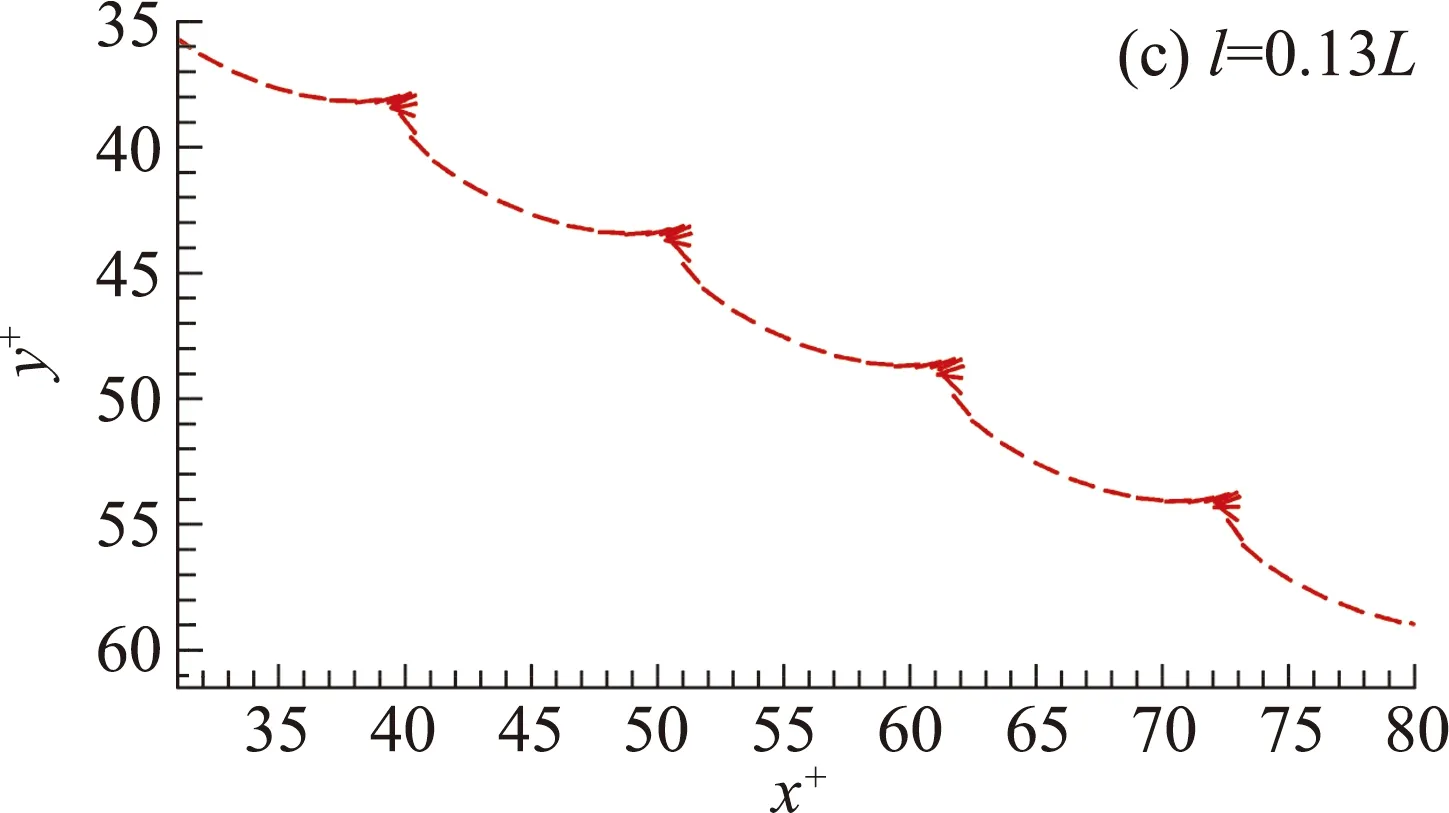
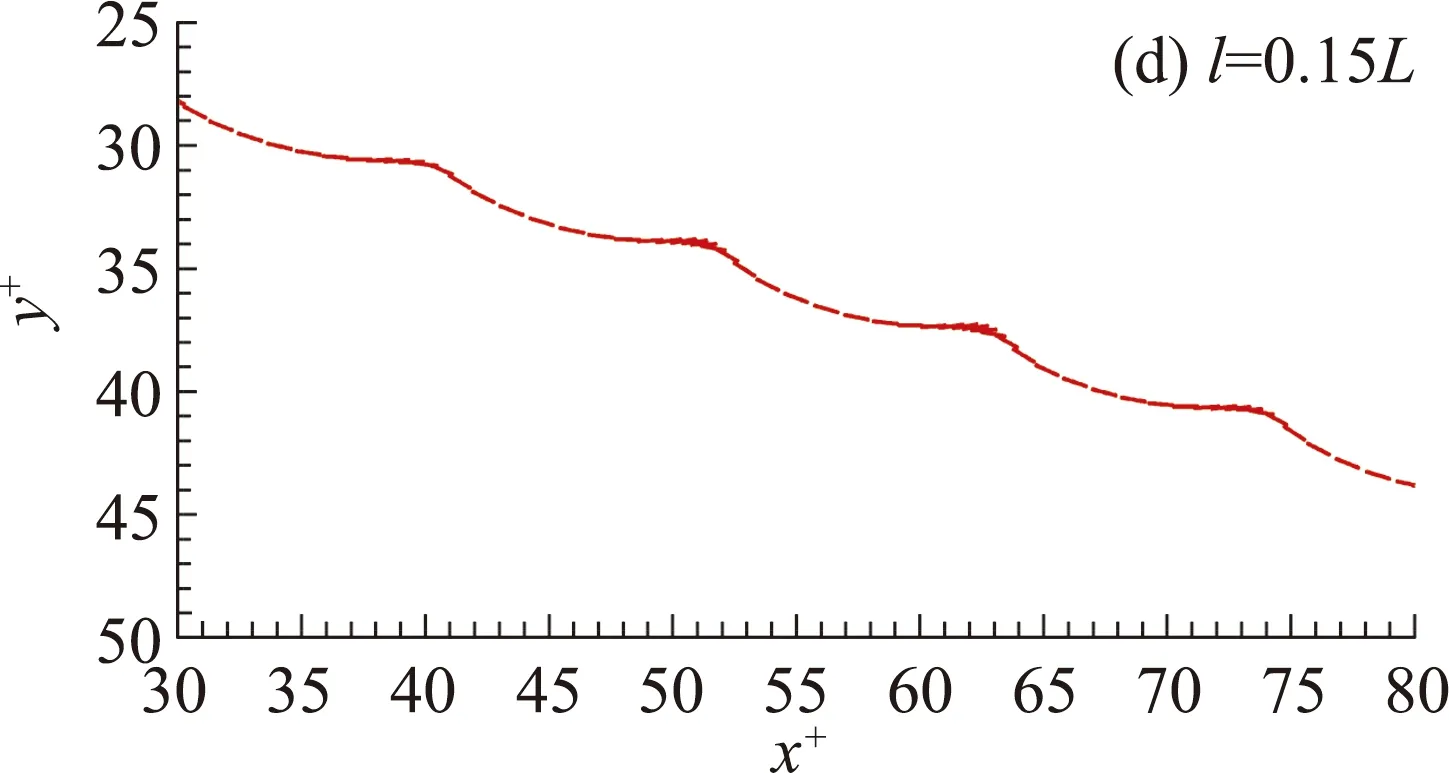
图5 质心偏移时下落运动轨迹Fig.5 Trajectories of freely falling plates (l>0)

图6 质心偏移动时无量纲速度u+-v+曲线Fig.6 u+ versus v+ (l>0)

结果显示，当质心位置稍偏离平板中点时(如l=0.01L，图5a)，平板的摆动运动出现了较小的不对称，这一不对称也同样体现在速度的周期性变化中(图6)。随着质心位置逐渐偏离(如l=0.04L，图5b)，摆动运动的不对称越来越大，摆动在一侧的特征越来越不明显，而另一侧反之；当l=0.15L时(图5d)，一侧的摆动已经消失，此时的平板下落运动已经近似翻滚运动。这个单侧摆动逐渐消退的变化过程在u+-v+曲线有明显体现(图6)——随着质心位置的偏离，“∞”形轨迹的左侧逐渐萎缩直至消失，退化为“o”形轨迹。特别是在摆动运动和翻滚运动转变的临界点附近(如l=0.13L)，u+-v+曲线上虽然还残存着“∞”形运动特征(图6)，但从运动轨迹上已经看不出摇摆运动(图5c)。也就是说，在质心位置偏离平板中点时，下落运动是一种特殊的摆动运动，根据其运动特征可称为“非对称摆动”。

图7(a)显示了I+=1.0、质心偏移l=0.01L时的平板自由下落运动轨迹。可见在翻滚运动的状态下，发生一定的质心偏移将会衍生出一种摆动和翻滚交替出现的复杂运动，根据其运动特征可称为“摆动-翻滚混合运动”，可简称“摆翻运动”。摆翻运动的u+-v+曲线呈现双“∞”形轨迹(图7b)。

(a)运动轨迹

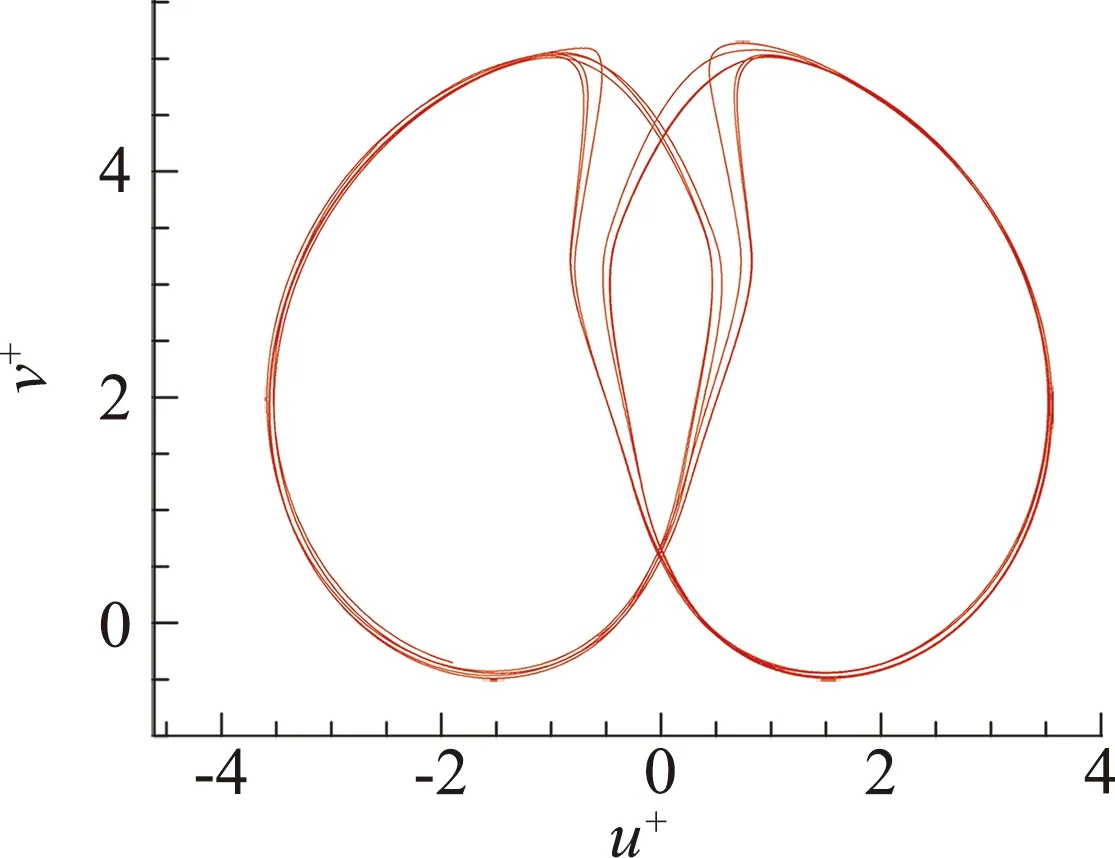
(b)u+-v+曲线图7 摆翻运动Fig.7 Flutter-tumbling

当质心位置偏离平板中点较远时(如l=0.25L)，平板保持竖直稳定的定常下落，未出现速度和位移的周期性变化。

3 讨 论

首先以质心位于平板中心、I+=0.0323的摆动状态为例，对平板下落过程进行气动力分析，图8显示了该状态下一个摆动运动周期中的无量纲速度、角度和气动力随时间的变化曲线。图8中可见，当平板摆动到最左侧时(tw=0)，存在一定的垂直速度而水平速度为0，角度约65°，此时平板状态相当于攻角25°,来流速度等于垂直速度。此时气动力方向偏右上，作用点偏平板右侧，相对质心产生正(逆时针)的气动力矩(图8)。同时，平板受到重力作用，气动力和重力的共同作用下使平板向右下方平动的同时逆时针转动(tw=0～0.25)。tw=0.25～0.5时同理也能产生相似的作用。反之，当tw=0.5～1时，平板的状态正好相反，产生了相反的作用。图9将这一作用过程详细直观地进行了描述，给出了典型位置的总气动力大小、方向和作用位置(括号中的值代表总气动力距平板质心力臂，下同)。在整个摆动过程中由于平板转动惯量较小，气动力矩产生较大的转动加速度，平板的转动能够较快地响应气动力矩变化，循环往复形成周期摆动。

图8 摆动运动时无量纲速度和气动力变化曲线Fig.8 Dimensionless velocities and aerodynamic force components of fluttering

再来分析翻滚运动的情况，图10以I+=1.0时为例显示了翻滚下落时的平板受力情况。平板向左侧运动的过程中，具有较大的水平速度，此时气动力略大于重力且方向相反，平板在惯性作用下保持平动且加速了顺时针转动，这一过程同摆动运动中相似(图9)。当平板运动到最左端时，受力情况也与摆动运动中类似(图9)，但由于平板转动惯量较大，逆时针方向的气动力矩仅仅减缓了平板的顺时针转动，因此平板仍然保持顺时针转动并逐渐回到上一状态，如此往复形成周期性翻滚运动。

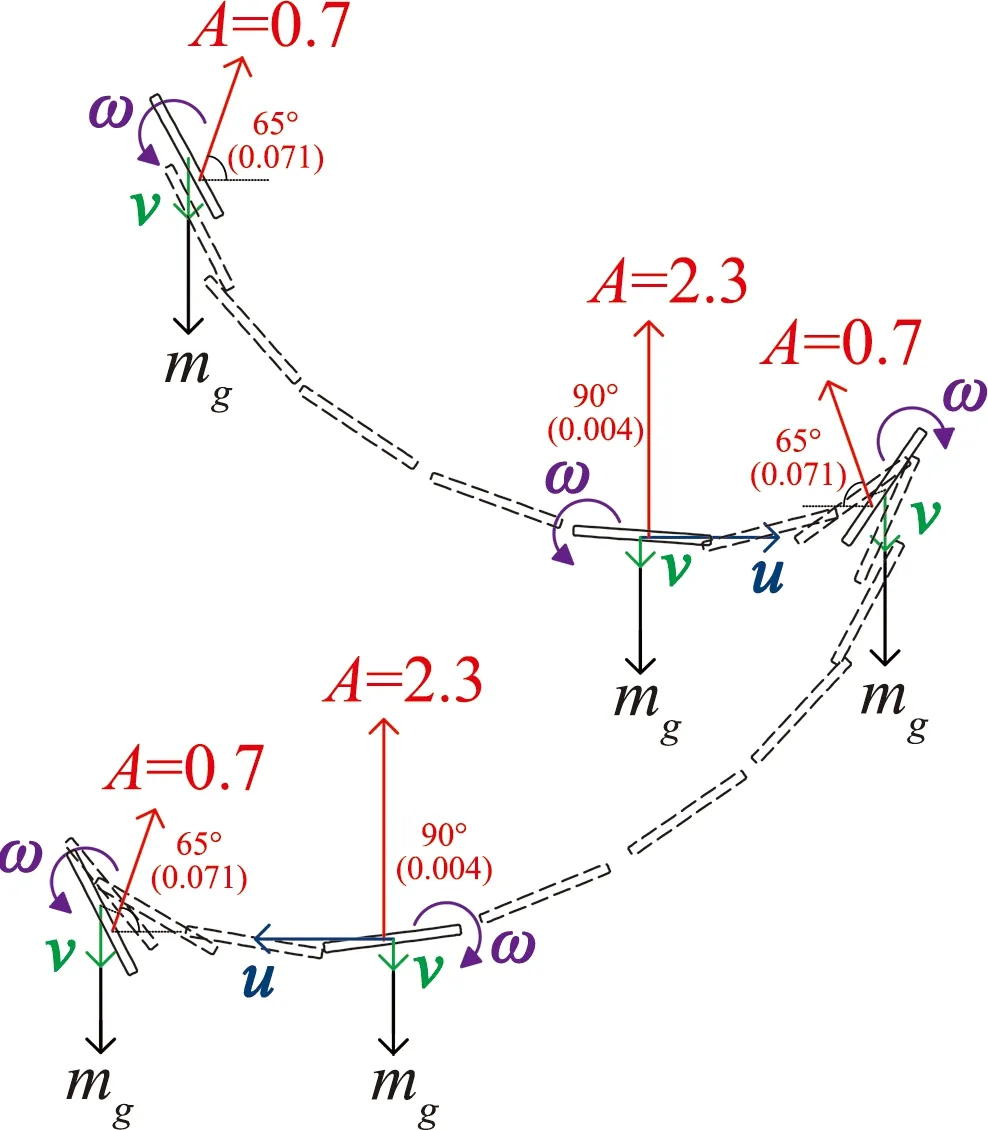
图9 摆动运动时平板受力情况示意图Fig.9 Plates attitude,forces,and velocities of fluttering

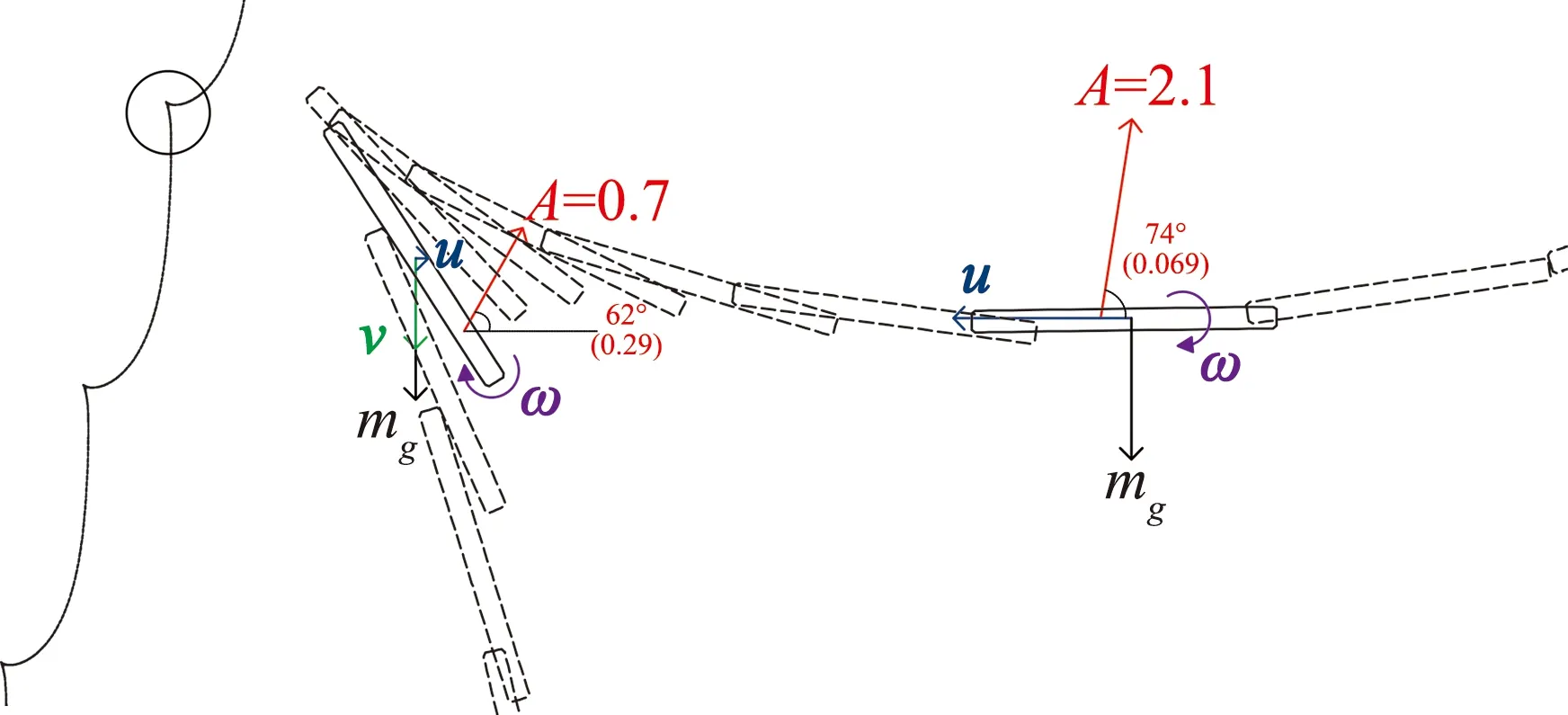
图10 翻滚运动时平板受力情况示意图Fig.10 Plates attitude,forces,and velocities of tumbling

接下来对非对称摆动的自由下落情况进行受力分析。图11中以图5(b)中非对称摆动下落时的状态为例显示了平板受力变化情况，其中基本过程与摆动运动一致，不同点在于：由于质心位置偏移，不仅重力的作用点发生了变化，同时导致了气动力相对质心力矩的左右不对称。在平板向右侧运动的过程中，气动力作用点距质心较近，气动力矩较小作用微弱，故摆动的速度、距离和时间较长；反之平板向左侧运动时，气动力作用点距质心较远，气动力矩较大作用明显，故摆动过程较短(图11)。这个过程周期变化形成了非对称摆动现象。

同理，摆翻运动看似复杂，但受力情况与摆动和翻滚运动类似，这里不再分析，简述如下：在摆动运动部分气动力作用点距质心较远，气动力矩作用大于转动惯性作用，造成了摆动运动；在翻滚运动部分气动力作用点距质心较近，气动力矩作用小于转动惯性作用，造成了翻滚运动。

最后，质心偏离平板中心较远时的定常下落可视为一种非对称摆动或摆翻运动的极限情况：摆动较短的过程(或摆动部分)消失，摆动较长的过程(或翻滚部分)增至无限。此状态中平板保持竖直下落，实际攻角和转动速度为0，气动力和重力作用于一条直线上，平板在合力作用下保持定常下落状态。

图11 非对称摆动运动时平板受力情况示意图Fig.11 Plates attitude,forces,and velocities of asymmetrical-fluttering

4 结 论

本文利用动网格技术，耦合求解N-S方程和运动方程，对二维平板的自由下落问题进行了研究，数值模拟出了以往实验研究结果[1,2,5,11]中出现的两种规律运动：摆动运动和翻滚运动。主要结果如下：

1)无量纲转动惯量和平板质心位置是决定平板自由下落运动方式的重要参数。其中，无量纲转动惯量I+≈0.95是摆动运动和翻滚运动转变的临界点；

2)非匀质平板质心位置偏离中点时，平板自由下落出现新的、衍生于摆动运动和翻滚运动的规律下落运动，根据其运动特点可称为非对称摆动和摆翻运动。