自动编码器在流场降阶中的应用

叶舒然,张 珍,宋旭东,杜特专,王一伟,*,黄晨光,陈耀松

(1.中国科学院力学研究所 流固耦合系统力学重点实验室,北京 100190；2.中国科学院大学 工程科学学院,北京 100049;3.北京大学 工学院,北京 100871)

0 引 言

机器学习作为计算机科学领域中一个备受关注的研究方向，其核心主要是使用算法解析数据，并利用计算机的大信息处理能力从原始数据中提取模式。近来，机器学习在许多领域得到蓬勃发展，例如在自然语言处理和各类图像识别等方面已经得到广泛应用[1]。机器学习在流体力学中的应用也开始逐渐浮现，Tracey等[2]利用神经网络拟合Spalart-Allmaras湍流模型并证明了其能够优化计算流体力学中得到的结果；Ling等[3]提出使用嵌入伽利略不变性的多层网络预测雷诺应力张量，并取得了更为精确的结果。至此，机器学习在流体力学中的初步尝试主要是通过前馈神经网络构建湍流模型。

由于流场的复杂性，除了关注于传统前馈网络学习算法，利用机器学习中的各种方法来探索流场识别、提取、降阶也是一个非常重要的方向。以卷积神经网络为代表的深度网络在流体力学中有了一些新的尝试。Storfer等[4]使用卷积神经网络成功识别了流动特征，并且识别出的特征能够与相似特征进行区分。Jin等[5]构建了一个捕捉绕流圆柱表面压力系数时空信息的卷积神经网络，能够成功捕捉压力脉动特征并预测速度场信息。对于流场建模，除了直接寻找数据间的映射关系，基于无监督思想下的寻找数据之间的特征提取技术也是一种建模与降阶技术[6]。例如Kaiser 等[7]提出了一种无监督学习下用以识别流场物理机制的CROM方法，这种方法在三维钝体湍流尾迹和空间演化的不可压混合层的速度场都进行了成功的应用。考虑到自动编码器作为一种典型的数据压缩与降维方法，在图像和自然语言处理等方面有很好的实践，因此探索自动编码器在流场降阶中的应用。将自动编码器引入流场，建立流场速度场的编码和解码模型，能够将原始高维数据进行压缩，并且能够对流场实现一种通用的降阶方法。

本文以圆柱浇流流场的速度场为输入，建立了自动编码器模型，对全场的速度场分量进行编码和数据降维，最后与流场特征量构建的网络进行了误差分析，分析了自动编码器的数据降维和特征提取的合理性。该方法在一定范围内的速度入口和雷诺数条件下，能够为流场数据的表示提供合适的编码函数。并且，结合深度学习技术，能够得到相关的流场特征识别与提取结果。

1 自动编码器原理与设计

自动编码器是一种神经网络，这种网络的特点是在经过训练后能够将输入复制到输出[8]。作为无监督的一种网络模型，自动编码器能够从输入数据中学习到隐含的数据特征，并且由这些特征重构出原始数据。因此，自动编码器在数据降维和特征学习等方面有着广泛的应用。

1.1 前馈网络结构

自动编码器可以被看作是前馈网络的一个特例[9]。因此，首先建立一个全连接的前馈网络，其网络结构如图1(a)所示，分为输入层、隐层、输出层，上一层的任何神经元与下一层的每个神经元都有连接[10]。神经元模型的概念来自于生物神经中，通过电位变化传递信息[11]。对于神经网络模型中的神经元模型，其权重函数和偏置向量，用方程表示为：

f(x;w;b)=xTw+b

(1)

式中，w为权重系数，b为偏置向量。

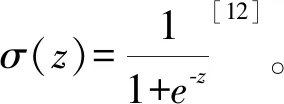
神经网络将输入层数据通过映射转换到隐层，再逐层转化到输出层。网络的输出和真实值之间的差异用损失函数衡量[13]，对于常见的回归问题,一般取为网络预测值和参考值之间的均方根误差：

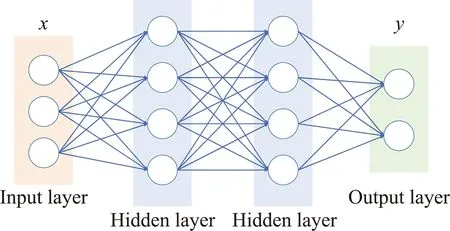
(a)网络结构

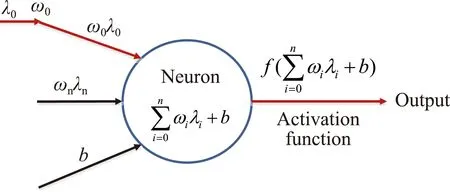
(b)神经元图1 前馈神经网络Fig.1 Feedforward neural network

(2)

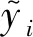
1.2 自动编码器设计

前馈神经网络，如果其只有一个隐藏层h，则该网络可以看作为从输入到隐层的映射函数h=f(x)和隐层到输出的映射函数y=g(h)。由于自动编码器的特点是能够将输入复制到输出，所以在网络中将输出设计成与输入相同，并将隐层的节点数设置成比输入输出的节点数少，通过训练调整权重系数，得到每一层的参数，便可以获得原始数据在小维度上的表示。对于该网络而言是一个编码和解码的过程，即将原始数据进行压缩，再从压缩的数据中还原。

图2是自动编码器的网络结构，在该网络中输出与输入相同，即y=x。自动编码器的训练方式和一般前馈神经网络完全相同，即使用小批量的梯度下降算法，使输出y逐渐贴近输入x[15]。网络训练完成后，能够得到一个输入到隐层的编码模型和一个隐层到输出的解码模型，隐层的节点信息即为最后的编码结果。考虑到编码的稀疏性，在自动编码器的基础上加上稀疏性约束，编码结果中只有一小部分神经元被激活，大部分节点为0[16]。

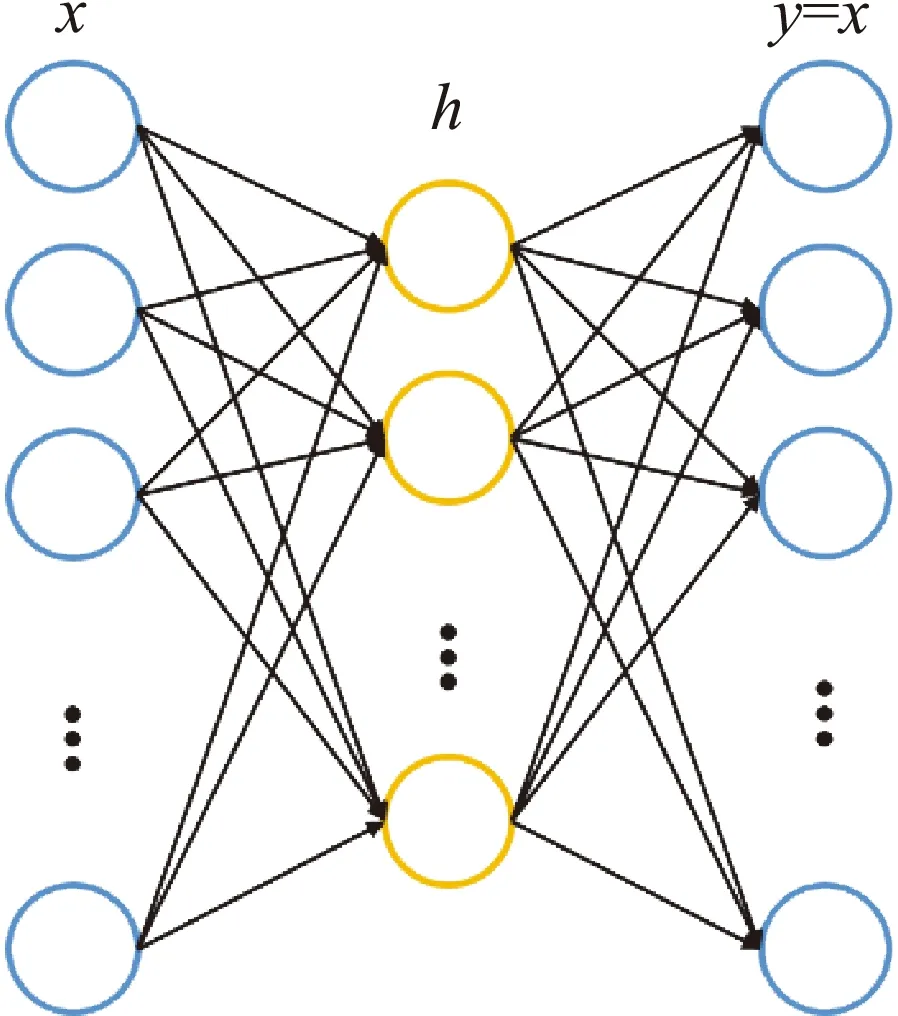
图2 自动编码器网络Fig.2 Autoencoder network

2 圆柱绕流自动编码模型建立

2.1 圆柱绕流算例

选取圆柱绕流的案例，构建流场并获取流动数据[17]。流场几何设置如图3(a)。考虑圆柱后41×17的速度场作为输入。由于是二维算例，对于每个点都有U={u,v}两个速度分量。流场的速度入口，考虑了带有扰动的抛物速度入口条件，其中3个速度入口作为训练，第四个速度入口作为测试。每个速度入口考虑雷诺数从200到2000的10组雷诺数，所有工况下均每隔0.005 s时间步长输出一组数据，共取300组数据。速度入口条件为基本抛物线速度入口乘以扰动因子P再归一化，基本抛物线速度入口为：

(3)

其中um=1.5。扰动因子P见表1。

表1 圆柱绕流流场不同速度入口条件Table 1 Different inlet velocity conditions of the flow around the cylinder

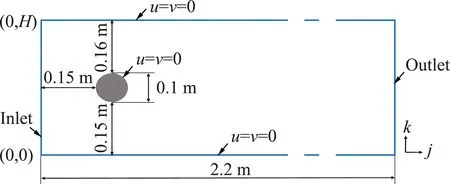
(a)几何尺寸和边界条件

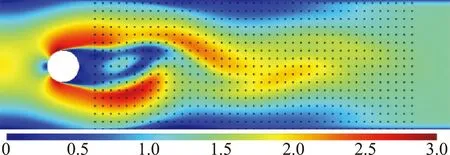
(b)圆柱后流场41×17的速度采样点分布

(c)圆柱上32个压力系数采样点分布图3 二维圆柱绕流算例Fig.3 2D cases in the flow around the cylinder

网络分为自动编码器和验证网络两部分，自动编码器考虑将41×17×2个速度分量通过自动编码，压缩为32个数据。验证网络将用编码后的数据与流场特征典型量相联系，讨论压缩处理后的数据是否抓住了原始数据中的主要特征。

2.2 自动编码器结构

对于圆柱绕流流场，采取上述的速度场进行描述，考虑到是二维流场，则在41×17个空间位置上共有1394个速度分量，对于其余的研究而言速度信息的维度过大，因此，寻找一种将1394维的流场速度数据进行压缩的方法十分重要。自动编码器结构能够将数据进行压缩，并且能够利用网络将数据还原。考虑到自动编码器的这个优势，使用自动编码器将流场速度分量压缩为只有32个值。因此对于网络，输入和输出选择各为1394个节点，中间隐层选择为32个节点，网络中通过选取不同的激活函数来添加约束，使得重构后的数据与原始数据非常接近但又有一些不同，以此强制模型考虑输入数据中哪些量需要被优先复制，达到增强网络性能的目的。

2.3 编码器验证与应用方法

对于自动编码器得到的缩减结果，一个很好的验证方式是，将经过解码后的数据与原始数据比较，得到两者间的均方根误差(Root Mean Square Error,RMSE)。由于流场信息的复杂性，想要探究缩减后的结果对于原始数据是否具有代表性，另一个验证方法是建立编码后数据与原始流场的对应关系。如果编码后的数据能够代替原始范围内的速度场信息，那么可以建立函数关系Cp=F(Uencode)，其中Cp是用入口平均速度无量纲化的压力系数，Uencode为编码后的低维流场。基于这种考虑，建立了全连接的神经网络，输入层为编码后的流场速度，输出层为圆柱表面压力系数。如图3(c)所示，圆柱表面压力系数选取为圆柱一圈32个离散点的值进行表示。由于训练集和测试集选取了不同的速度入口，为了防止入口速度变化对圆柱前缘处压力系数影响较大，在32个点中舍弃圆柱了迎着来流的6个点。圆柱表面压力采样点排列顺序是以迎来流最前端为第一个点顺时针等间距排列，因此在序号上体现为舍弃前后端的三个，并对剩下的26个点按照相同的顺序重新编号为1～26。这些点仍能覆盖圆柱表面大部分压力情况，并且不会使得速度入口所产生的误差对整体误差起到了主导作用。验证网络选取了单隐层的128个节点的验证网络1，和隐层的数量为2层、每层30个节点的验证网络2，并加了dropout层以防止过拟合。验证网络结构见表2。

表2 验证网络的网络结构Table 2 Network layers of the verification network

3 圆柱绕流自动编码器的应用

输入训练数据完成网络训练后，需要应用测试数据测试网络的可靠性。本文的自动编码器在流场中的应用主要分为两个方面，一方面关注了自动编码器编码解码过程中的精度，是否能生成与原始流场精度差异较小的重构流场，另一方面也考虑到编码过程是否能够对原始流场进行成功的压缩降阶，并通过关联流场中的某些敏感关注量考察编码器能否代替原始流场。具体流程见图4。

图4 自动编码器应用流程图Fig.4 Flow chart of the application of the autoencoder

3.1 自动编码器的表现

上述圆柱绕流案例有10组雷诺数，每组雷诺数每隔0.005s取一组数据，共计算了300步数据。为了防止训练集对于速度入口过拟合，共考虑了4个不同的速度入口，3组进行训练，1组进行测试，即训练样本数为9000，测试样本数为3000。

自动编码器的结构采用的是2.2节中所描述的网络结构。图5可以看出，随着训练步数的增加，训练过程中的均方根误差即损失函数在逐渐下降，经过100步的迭代误差已经降到1.2×10-2，并有继续下降的趋势。

网络训练完成后，将测试数据的速度场输入网络模型，即可得到测试数据在自动编码后的系数，其均方根误差δRMSE为1.45×10-2。可以认为测试数据在经过编码和解码之后能得到与原始数据误差较小的结果。随机选取Re数为700的一个速度场进行研究，从速度云图上看,其中图6(a)为原始速度场的速度u分量的速度云图，图6(b)为重构速度场的速度u分量的速度云图，可以看出该编码解码过程误差较小，说明编码后的数据能够包含大部分流场信息。

同时，我们将编码维数增加一倍，使用自动编码器将流场速度分量压缩为64个值，并使用64维数据重构流场，如图6(c)。可以看出编码维数的增加，能够使得重构出的流场更好地呈现原始流场的流动特征，例如在核心区外围的情况能够将流场信息把握得更好。

图5 网络的训练误差Fig.5 Training error of network

(a)原始流场

(b)重构流场1

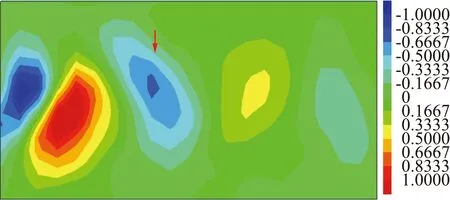
(c)重构流场2图6 速度分量u的速度场云图Fig.6 Velocity contour of velocity component u

3.2 基于压力回归的网络验证

自动编码器训练和测试完成后，进一步利用前述的压力回归方法对编码器表现进行验证。对于验证网络，训练集和测试集的数据来源依旧是上述雷诺数和速度入口组合下的工况。对于每组数据，输入由原始的1394个速度分量缩减为编码后的32个组合值，输出则考虑到需要对原始流场信息进行表征，因此选取了圆柱表面26个点的压力系数。分别用2.3节所述的两种网络结构进行了验证，其中编码后数据在验证网络上的表现如表3所示。

表3 训练集和测试集分别在验证网络上的均方根误差Table 3 RMSE for the train set and the test set on verification network

3.3 与随机取点对比

为了验证自动编码的效率，将流场的41×17×2个速度分量中随机选取32个点作为对照组，其中随机选取的过程保证所取点在训练数据和测试数据中代表的意义相同，即在固定空间位置上的相同速度分量。

通过对比2.3节所建立网络与随机取点，分别得到了单层编码结果和随机取点在验证网络上的均方根误差。表4中对比了两种网络上测试集的误差。图7选取了某时刻预测的压力系数与实际值的对比。自动编码器的残差约为随机取点网络的一半，说明了自动编码器的压缩算法能够更有效表达原流场的信息。

表4 单层编码和随机取点在验证网络上的均方根误差Table 4 RMSE for the encoded result and the random-sampling on verification network

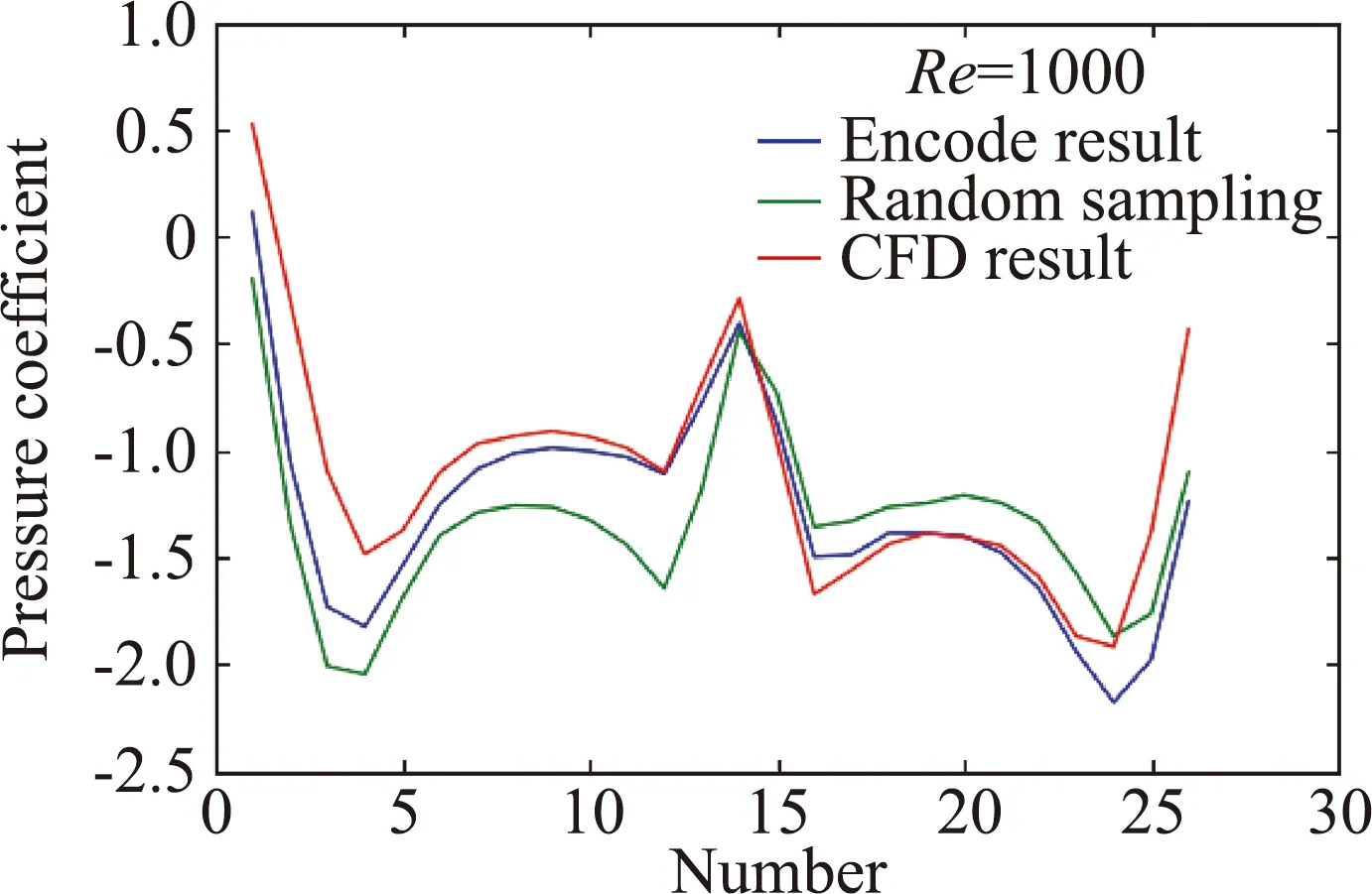
图7 单层编码与随机取点在验证网络上预测结果与CFD参考值结果中圆柱压力系数分布的比较Fig.7 Comparison of pressure coefficient distributions on the cylinder between the CFD result,the model predictions of the encode result and the random sampling

4 编码层层数影响分析

4.1 网络结构

前文中采用的是基本的单层编码器和解码器，但实际上对于复杂问题，深度的编码器和解码器也具有一定优势，能够更好地体现深层网络的可控性，在拟合数据过程中较大地降低训练的计算成本和所需的训练量。例如，Hinton等[18]提出在实验中，深度自编码器能够比相应浅层的编码器拥有更好的压缩效率。

对于速度场信息压缩的问题，为了探究自动编码器网络对编码效率的影响，提出了一个隐层数为5的网络，新的编码器网络结构如表5。在该网络中，编码器和解码器均为3层网络。

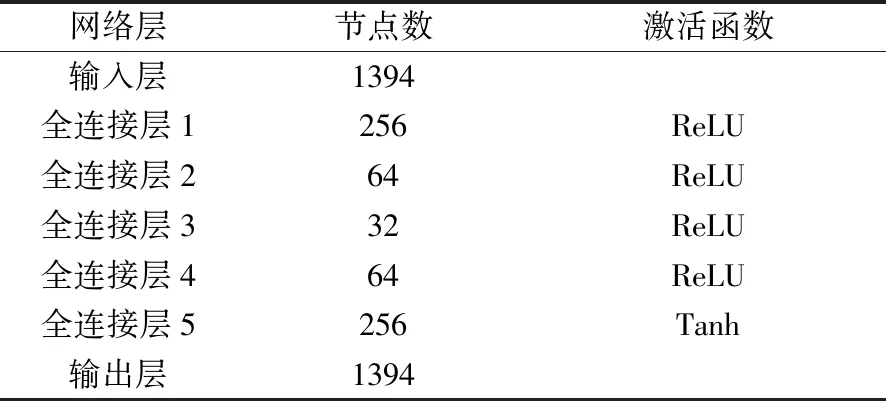
表5 自动编码器的网络结构Table 5 Network Layers of the autoencoder

4.2 结果对比与讨论

训练深度编码模型，其本质是训练具有更多中间层的网络。对于流场速度场数据，网络的输入是1394维特征，与单层编码不同的是，深度编码网络中三个隐含层维度分别为256、64和32，即通过逐步降低输入数据的维度，得到最终编码后的32维的低维数据。表6对比了单层编码和深层编码在编码网络(AE-Net)和验证网络(Verif-Net)上的均方根误差，可以看到，在最终维度相同的情况下，深层编码与单层编码相比，重构出的数据误差更小，且能够更好地捕捉数据的特征，压力回归测试均方根误差小于0.1。但由于目前算例相对简单，深度编码器体现出的优势并不十分明显。

表6 单层编码和深层编码网络的均方根误差Table 6 RMSE for the single layer encoded result and the multi-layer encoded result

5 结 论

本文提出了一种将自动编码器应用在流场中的方法。该方法通过将高维的原始速度场编码为少量点的低维数据，并对数据解码，能够对原始流场进行重构。对非均匀来流圆柱绕流算例建立的典型单层自动编码器模型，重构流场与原始流场速度均方根误差小于0.02。

本文证实了通过自动编码器将原始高维流场进行降阶和数据压缩，可以将压缩后数据与原流场中的敏感输出值相关联。对此基于圆柱绕流流场自动编码器的应用，建立了利用降维后编码数据来回归圆柱表面压力分布的神经网络测试。结果表明编码数据能够较好地回归到圆柱的表面压力系数，且回归精度明显高于利用同等数量随机测点进行回归的对照模型。

最后考虑到更复杂流场的编码需求，讨论了编码层层深对于编码效果的影响。典型的不同结构编码器对比结果表明，五层结构的深层编码器比浅层编码器在编码网络上的误差更低，编码精度更高；同时在与流场敏感输出值相关联时网络预测误差能够达到0.1，对原始数据的代表性也更好。

未来，本文所建立的基于机器学习的自动编码器方法有条件应用于更复杂的流场结构的识别与降阶，应用的范围与方式值得进一步讨论研究。此外，如将自动编码器与潜变量模型理论结合，则可进一步应用于流场生成模型的构造，值得进一步探索。