指数平滑结合条件Markov预测模型研究——基于新疆货运量预测

（新疆财经大学，乌鲁木齐市，830012） 吕冬梅

1 前言

目前马尔科夫模型主要运用在语音识别、股票预测、环境质量、文字信息、信息安全等方面[1-3]，这些具体实例应用的方法主要是利用马尔科夫理论具有平稳性的特性，并利用经验概率来创建初始概率分布和状态转移矩阵，从而构造马尔科夫模型，进而进行具体问题的预测研究。陈嘉晋[4]等利用马尔科夫链模型来预测股票价格未来短期变动趋势，得出马尔科夫链模型在短期股价预测方面总体令人满意。何众颖等[5]建立三次指数平滑与灰色马尔科夫链预测模型相结合，建立船舶到港量的灰色马尔科夫链优化预测模型。刘历波[6]等提出一种灰色-马尔科夫预测模型，并结合河北省某地区的159 座桥梁数据进行预测，得出该方法具有更高的精度和稳定性。本文提出一种条件马尔科夫模型与三次指数平滑相结合的预测方法，通过三次指数平滑的预测结果来确定条件马尔科夫模型中的条件一步状态转移矩阵，最后结合新疆货运量数据进行应用检测。

2 理论介绍

指数平滑法（Exponential Smoothing，ES）是布朗（Robert G..Brown）所提出，布朗认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延；他认为最近的过去态势，在某种程度上会持续到未来，所以将较大的权数与近期数据做匹配。指数平滑法是生产预测中常用的一种方法，也用于中短期经济发展趋势预测，在许多经济预测方法中，指数平滑是用得较多的一种。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；而指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。一般常用到的指数平滑法为一次指数平滑、二次指数平滑和三次指数平滑。

2.1 确定初值

不管什么指数平滑都会有个初值，假如数据大于20 项，那么初值就可以认定为第一个数据，或者利用下列公式计算也行；假如数据小于20 项，则初始值为：

2.2 确定指数平滑系数α

指数平滑系数的确定一般依赖于四条规则：

（1）当时间序列呈现较稳定的水平趋势时，应选较小的α，一般可在0.05～0.20之间取值；（2）当时间序列有波动，但长期趋势变化不大时，可选稍大的α值，常在0.1～0.4之间取值；（3）当时间序列波动很大，长期趋势变化幅度较大，呈现明显且迅速的上升或下降趋势时，宜选择较大的α值，如可在0.6～0.8 间选值。以使预测模型灵敏度高些，能迅速跟上数据的变化；（4）当时间序列数据是上升（或下降）的发展趋势类型，α 应取较大的值，在0.6～1 之间。

2.3 预测模型

（1）二次指数平滑：

给定平滑系数，二次指数平滑的计算公式为:

预测未来期的值的计算公式为:

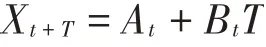
其中：

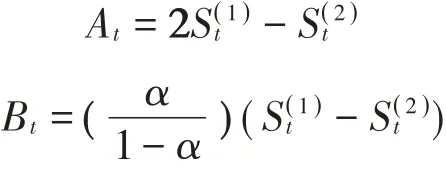
（2）三次指数平滑：

给定平滑系数，三次指数平滑的计算公式为：

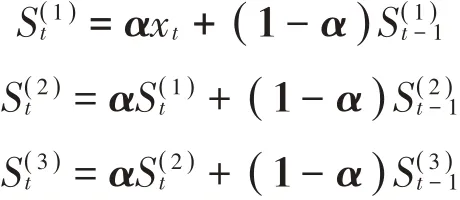
预测未来期的值的计算公式为：

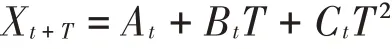
其中：

4、条件马尔科夫修正误差率原理

采用一步预测，只需求得误差率的状态一步转移概率矩阵，将其作为权重用于修正指数平滑法预测结果的误差，会使得误差减小，预测结果更加精确。

（1）一般状态转移概率修正误差过程

预测第t期，首先算出t期以前的一步状态转移次数矩阵

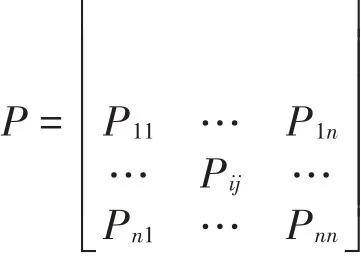
其中，Pij：状态i（Ei）转移到状态j(Ej）的次数。由该矩阵得到一步状态转移概率矩阵：

若t-1时刻状态为Ek，并且状态区间值对应值为Yk，则t时刻

（2）条件状态转移概率修正误差过程

第t-2 时刻状态为Ea，t-1 时刻状态为Eb，根据t时刻以前数据得到在t-2 时刻状态为Ea的条件下，t - 1 时 刻 状 态 为Eb，t 时 刻 由Eb转 移 到E1、E2、……En的状态转移概率矩阵Ebn，该矩阵为1*n的矩阵，矩阵内元素和为1，若矩阵和为0，则默认t 时刻状态仍为Eb，其中a，b=1、2、……、n。最终t时刻

3 新疆货运量预测应用

以新疆1995 年～2015 年的货运量这一指标数据为基础，用三次指数平滑结合条件马尔科夫链模型进行数值验证。

3.1 基础模型（指数平滑模型）的确定

数据容量小于20，则令初始数据为:

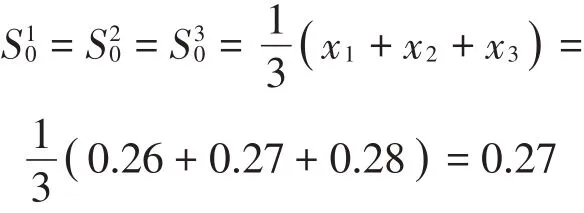
确定三次指数平滑模型的平滑系数。首先做趋势图，如图1所示：

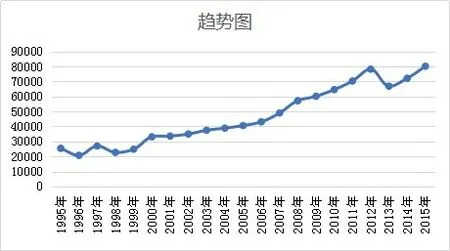
图1 时序图

从图1可以看出，该时间序列有较小波动，但长期具有较稳定的上升趋势，平滑系数应采用0.1 到0.4之间。为保证严谨性，本文在计算时，将平滑系数分别取0.1、0.2、0.3、0.4、0.5五个值代入三次指数平滑这一基本预测模型中，求得预测误差，结果如图2 所示。从图2 可以看出，当平滑系数取0.1 时，预测结误差是最小的，即效果最好。最终确定平滑系数为0.1。

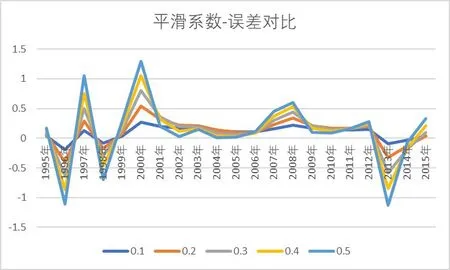
图2 不同指数平滑系数预测误差对比图

将二次指数平滑模型、三次指数平滑模型用于新疆货运量数据的预测，预测结果见表1。

从表1 中可以看出，三次指数平滑模型的总体预测效果优于二次指数平滑模型。三次指数平滑模型的预测结果显示，最大预测误差为26.91%，最小预测误差为-3.35%。二次指数平滑模型的最大预测误差为30.16%，最小预测误差为-3.40%。

二次指数平滑模型和三次指数平滑模型预测的误差结果如图3所示：

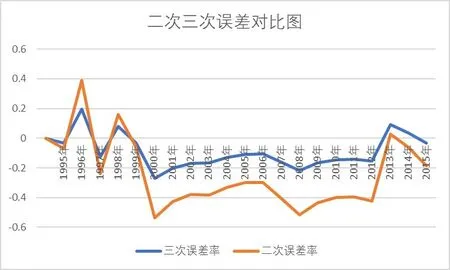
图3 二次三次误差对比图

表1 二次、三次指数平滑结果（一步预测）

表2 预测结果及误差表

如图3 所示，三次指数平滑模型的误差曲线波动更小，最终选择三次指数平滑模型为一步预测基础模型。

3.2 马尔科夫修正误差过程

由三次指数平滑模型（平滑系数为0.1）对1995年-2015年的货运量总量的一步预测误差区间为（-27%，20%），马尔科夫链模型最常设的状态个数为三到四个，鉴于误差区间较大，文中设置为四个状态。所以状态区间划分为：E1（-27%，-15.25%）；E2（-15.25%，-3.5%）；E3（-3.5%，8.25%）；E4（8.25%，20%）。

根据状态区间建立一步条件状态转移概率矩阵。

3.3 预测结果对比

基于2005～2015 年的数据，对条件马尔科夫——三次指数平滑预测模型、马尔科夫——三次指数平滑预测模型以及三次指数平滑模型三个模型的预测效果的检验。预测结果及预测误差见表2。

由表2 可以看出，三次指数平滑模型的预测结果的误差最大值为-21.61%，最小值为3.35%，平均误差率为10.04%，误差率在10%以上的比例为72%，一般马尔科夫修正误差后的预测结果的误差最大值为32.64%，最小值为-1.83%，平均误差率为0.45%，误差率在10%以上的比例为40%，条件马尔科夫修正后的预测结果的误差最大值为35.70%，最小值为-0.46%，平均误差率为0.39%，误差率在10%以上的概率为9%。综上可得，条件马尔科夫——三次指数平滑预测模型预测效果最好。

误差对比图如下所示：

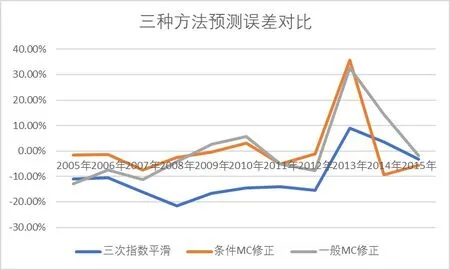
图4 预测结果误差对比图

从图4 中可以看出，条件马尔科夫——三次指数平滑预测模型在2005 年～2012 年的预测结果效果优于其他两种模型，2013～2015 年三次指数平滑结果优于其他两种，总体来说，条件一步状态转移概率修正过的三次指数平滑效果更优。

4 结论

运用马尔科夫链与BP神经网络、指数平滑、灰色模型等预测方法结合，采用的状态转移矩阵通常采用传统的状态转移矩阵，本文首先使用传统状态转移矩阵来修正三次指数平滑方法的误差，最终发现某些样本下，修正后结果差于修正前，随后采用本文新提出的条件状态转移概率矩阵来修正误差，最终比较三次指数平滑方法，传统状态转移概率矩阵修正三次指数平滑方法和条件状态转移概率矩阵修正三次指数平滑方法三者的预测结果，最终发现本文提出的新方法效果最好。并且如果样本容量更多，条件状态转移概率会更好的展现出它的优势。