基于遗传算法的高校教务系统排课问题的应用研究

蒋正锋，吕佩佩，覃韩，龚琼珍

（1.广西民族师范学院数学与计算机科学学院，崇左532200；2.武汉大学计算机学院，武汉430072）

0 引言

二十世纪五十年代就有学者对自动排课问题进行研究，如Gotlieb 在1963 年时第一次就提出了自动排课的数学模型，而我国对排课问题的研究起步比较晚，始于80 年代初，并且取得了一定的成效，一些学校都有自己的排课系统[1,5]，但是这些排课系统都是依赖各个学校的具体情况，有自己的特殊性[2]，不宜推广。考虑广西民族师范学院的教学体制，模拟人工排课过程，制定一份相对能够统筹兼顾学校教学资源的课表，将提高排课的效率，减少了排课工作量，提高学校教学质量，对推动学校信息化管理也起着重大的作用。

1 遗传算法

1.1 遗传算法的基本思想

遗传算法（Genetic Algorithms，简称GA 或GAs）[3]是在二十世纪七十年代初由美国密歇根大学的Joho H.Holland 教授首先提出来的，是一种模拟生物界的进化规律演化而来的随机化搜索方法，它刚被提出时便吸引了大量学者进行研究，并迅速得到推广到搜索、优化等领域。遗传算法是一种基于群优化的方法，在初始解集种群生成后，种群中的每个个体都会根据适应度函数[4]来评估优劣，将剔除种群部分个体，最后得到最优个体，就是待求解的最优解。具体优化步骤如下：

步骤一：随机生成初始化种群。

步骤二：根据求解问题的目标函数构造适应度函数。适应度函数用于评估种群中每个个体对其生存环境的适应性。

步骤三：根据适应度函数对种群个体的评估值，选择适应性强的种群个体，然后通过交叉和变异更新种群个体编码。

步骤四：循环执行步骤二、三多代后获得待求解的最优解。

1.2 遗传算法的基本操作

遗传算法主要包括三个基本操作[3]，分别为选择操作、交叉操作和变异操作，这三个基本操作是按顺序执行的，并且可以重复执行多次。

（1）选择操作

选择操作以种群个体适应度计算为前提，随机选择30%到60%的种群个体参与下一轮遗传操作。本文选择个体采用轮盘赌算法，基本思路是种群中每个个体被选中的概率与其计算出来的适合度成正比，然后以积累概率的形式分布在转盘上，通过转动转盘，选择指针落在某个扇区对应的个体。

（2）交叉操作

交叉操作是遗传算法的核心部分，它将两个父代个体以一定概率对基因编码[5]部分进行互相交叉重组，产生新的子代个体。交叉的方式有单点交叉、多点交叉和均匀交叉等，以单点交叉为例，两个二进制编码的个体分别为P1：10101101，P2：11010110，交叉前随机生成交叉位置n 和0 到1 之间的浮点数q。假设n=3，q=0.6，且0＜q＜0.8，则进行P1 和P2 的交叉操作，从P1和P2 从第四位开始交换所有后续的编码，生成新的个体为NP1:10100110，NP2:11011101，单点交叉操作前后如表1 所示。

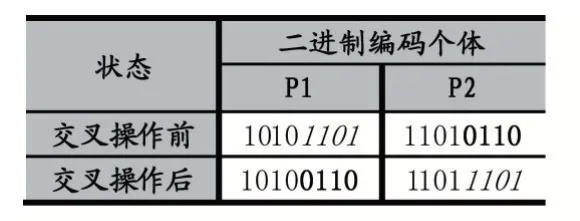
表1 单点交叉操作前后比较

（3）变异操作

变异操作是指以一定突变概率在一个父代个体基因编码的某个位置进行变异，生成新的子代个体。二进制编码的变异操作是0 变成1 或1 变成0。变异前随机生成变异位置n 和0 到1 之间的突变概率q。假设变异概率为0.06，n=4，q=0.03，且0＜q＜0.06，则对P3:11010011 进行变异操作，生成新的个体为NP3:10100110，变异操作前后对比如表2 所示。

表2 变异操作前后对比

遗传算法三个基本操作选择操作、交叉操作和变异操作如图1 所示。

2 排课问题制约条件

排课需要解决的问题，就是如何协调好时间与空间的关系[9]。课程表主要由五个要素组成，分别为班级、课程、教师、教室和时间。排课问题的五要素用集合形式表示，如班级CLASS={CL1,CL2,CL3,…,CLN}，课程COURSE={CO1,CO2,CO3,…,COL}，教师TEACHER={TE1,TE2,TE3,…,TEK}，教室CLASSROOM={CR1,CR2,CR3,…,CRP}，时间TIME={TI1,TI2,TI3,…,TIQ}，五要素之间存在一定的约束，排课问题就是在硬性制约和软性制约条件[3]下，寻找一个五要素之间的最优的组合。

图1 遗传算法流程图

（1）硬性制约

硬性制约是为了排除五要素之间出现冲突的情况，课程安排必须要满足的，如下列的情况：

①一个班级不能同一个时间片安排两门课程。

②一个教师不能同一个时间片教授两门课程。

③一个教师不能同一个时间片教授两个班级，合班授课除外。

④一个教室不能同一个时间片有两个班级上课，合班上课除外，但只能是一位教师授课。

⑤授课教室的容量要大于等于在此上课班级的学生人数。

⑥教室类型要与课程对教室要求的类型一致。

（2）软性制约

软性制约是在硬性制约的基础上人为设定的约束条件，是为了课程安排更加科学与合理，常见的软性制约如下：

①一个班级的上课时间不能过于密集，应均匀分散在一周内。

②同一门课程不同班级，授课教师在一天内完成相同的授课内容，以保证教学的连贯性。

③同一门课程同班级两次课时间间隔至少一天，但也不能超过两天。

④选修课安装在晚上或者周末。

⑤尽量满足教师对课程安排的特殊需求。

⑥连续上课或授课时，教室之间的距离不能太远。

⑦专业课和逻辑思维性强的课程，尽量安排在上午，体育课一般安排在下午。

⑧教师的授课任务不能过于集中，为保证授课质量，应均匀分散在一周内。

3 基于遗传算法的自动排课模型设计

3.1 基因编码

基因编码[6,7]是排课问题的五要素集合中元素的结构化组合。时间要素TIME 是由时间片TIi 组成的，每个时间片就是两节课，每天上午2 个时间片，下午2 个时间片，晚上1 个时间片，一周排课5 天，总共25 个时间片，排课问题就是基因编码分布在25 个时间片里，所以基因编码不包含时间要素。

3.2 生成初始种群

初始化种群就是随机生成一定数量满足硬性制约可用的全校课表的过程，一定数量是种群的大小，即个体的数量为M。

下学期要开设哪些课程是教研室主任根据培养方案来制定合理的任课计划表，而任课计划表中教师的授课任务是确定的，即在哪些班级开设了什么课程是确定的，所以班级、课程和教师的组合编码排课前就绑定好了。初始化种群是在满足硬性制约条件下把由班级、课程、教师、教室和时间组合基因编码保存下来，把班级、课程和教师看成一个新的组合要素，排课问题的五要素就转成了新的组合要素、教室和时间三要素，即新的组合要素和合适的教室构成的基因编码分布在某个时间片里。

生成一个初始化班级课表，具体操作过程如下：

步骤一：一个班级任课计划表中存在还没有安排的课程，转到步骤二，否则转到步骤五。

步骤二：选择其中一门课程，任课计划表中组合编码分成班级编码和新的课程和教师的组合编码，其中班级编码确定要初始化个体行的位置。

步骤三：随机选择一个满足硬性要求的教室，由课程、教师和教室构成基因编码。

步骤四：随机选择一个空闲的时间片，把基因编码写到时间片里，转到步骤一。

步骤五：班级课表初始化结束。

上述操作过程是初始化一个班级课表，循环操作初始化全校所有班级课表就生成一个种群个体，循环操作初始化M 个个体，就生成初始种群。

3.3 适应度计算

初始化种群后，对种群中个体的优化[4]，需用到适度函数来评估每个个体的适应度值。本文定义的适应度函数是基于加分原则的，满足不同软性制约条件则加上不同的分数，最后得到个体的适应度值。适应度的计算包括班级适应度、课程适应度和教师适应度。

（1）班级适应度考虑连续两门课程上课教室分布情况，如同一上课教室、同一楼层不同教室、不同楼层教室和不同教学楼的教室。

（2）课程适应度考虑课程分布在25 个时间片里的均匀程度，同一门课程两次课的间隔、不同类型课程如专业课和逻辑思维性强的课程、体育课等课程的安排、不同时间片对上课效果的影响等。

（3）教师适应度考虑授课分布在25 个时间片里的均匀程度、连续时间片授课不同教室的转移、同课程不同班级课程安排是否为同一天等。

对于一个班级来说，综合计算班级适应度和课程适应度，而对于一个个体来说，还需考虑教师适应度。

3.4 遗传算法优化课程表

遗传算法优化课程表就是循环选择操作、交叉操作和变异操作[6,8]三个基本操作，直到满足遗传算法结束条件。在排课问题中交叉操作和变异操作后都可能发生冲突，所以要进行冲突检测和调整，使交叉操作和变异操作后生成新个体满足硬性制约[3]条件。

（1）排课问题选择操作

根据种群中个体的适应度值使用轮盘赌算法选择种群中50%的个体进行下一步操作。

（2）排课问题交叉操作

本文成对发生交叉的概率设定为0.6，如发生交叉操作，排课问题的交叉操作有两种，一种个体与个体之间，随机互相交换某个位置后续班级的课程表，另一种是个体中同一时间片里基因编码中教室编码的互换，生成新的个体，加入到种群。

（3）排课问题变异操作

变异操作在优化种群极为关键，本文变异概率设定为0.5。排课问题的变异是指两个方面的变异操作，一是基因编码在时间片上的位置变化，另一个是基因编码中教室编码的改变。

（4）淘汰适应度低的个体

个体的适应度值是班级适应度、课程适应度和教师适应度值之和，计算出每个个体适应度，对种群中个体按适应度进行排序，淘汰掉适应度值低的个体，使种群大小为M，准备下一代的遗传操作。

3.5 遗传算法终止条件

淘汰适应度低的个体后，判断是否满足遗传算法的终止条件。本文遗传算法的终止条件有两种，一是进化迭代次数达到一定值后就结束遗传算法；二是连续进化迭代五次，种群中个体的最高适应度几乎没有变化。

4 基于遗传算法的排课系统

本排课系统采用B/S 结构，基于Java 语言开发的，采用JSP 技术和MySQL 数据库，开发出一个基于遗传算法的排课系统。

排课系统面向的学校管理人员、教师和学生，所以根据使用系统用户对象的不同，整个系统分管理员操作模块、教师操作模块和学生操作模块，用户登录界面如下图2 所示。不同用户登录进入不同的操作模块，管理员操作模块是自动排课系统最重要的部分，操作权限属于管理员。

图2 基于遗传算法的排课系统登录界面

管理员成功登录后，进入管理员操作界面，主要有排课管理、课程管理、课表管理、人员管理和基础数据管理等功能，系统功能主界面如图3 所示。

图3 排课系统功能界面

自动排课保存到数据库中的课表是班级课表，课表分班级课表、教师课表和教室课表三种，但教师课表和教室课表可由班级课表变换得到。某教师登录排课系统查看自己授课任务的课表如图4 所示。

图4 教师查看自己的课表

自动排课是本系统最为核心的部分，以班级、课程、教师和教室数据为基础，生成一定数量满足硬性制约可用的全校课表，然后使用遗传算法优化课表，可对生成的课表进行查看、修改、检查等操作，最终将课表数据保存到系统数据库中，能快速地自动编排成较科学与合理的课程表，符合教学规律，对于提高学校教务管理水平具有重要意义。

5 结语

如何合理配置有限的教学资源已成为每个高校[5,6]避不开的问题，其中编排全校科学与合理的课程表是这个问题的核心部分。本文简单介绍了遗传算法的基本思想，对排课问题的制约条件进行了分析，针对广西民族师范学院的具体情况，结合遗传算法中选择、交叉和变异策略进行分析，设计了一个基于遗传算法的智能的自动排课数学模型，由测试结果表明了该智能排课模型能快速地自动编排成较科学与合理的课程表，省时又省力，但随着学校快速发展及招生规模的进一步扩大，学校教务管理工作的变化，排课问题需求也会发生变化，因此排课问题的算法有待于进一步优化和研究[7,10]。