自适应RBF 神经网络在模拟电路故障诊断中的应用

文怡婷，严太山，李文彬

（湖南理工学院信息科学与工程学院，岳阳414006）

0 引言

模拟电路是用来对模拟信号进行传输、变换和处理的电路，它是电子电路的基础。相对于数字电路来说，模拟电路出现的故障率较高，而且故障信息呈现噪声高、特征多、非线性的特征，使得模拟电路故障不易诊断，成为电路研究中的热门领域，已有不少学者投入到模拟电路故障诊断的研究中，提出了诸多有价值的模拟电路故障诊断方法。其中，常规的故障诊断方法如故障字典法、参数识别法、网络撕裂法等，由于其局限性已不再适用[1-6]。

神经网络技术的兴起，为解决故障诊断问题提供了一条新的途径。神经网络系统具有强大的I/O 非线性映射、信息分布存储和并行处理功能，特别是其高度的自组织和自学习能力，使其为模拟电路诊断提供了全新的理论方法和实现手段[7-12]。在各种神经网络中，RBF 神经网络是一种性能良好的三层前馈神经网络，已经证明它具有较好的全局逼近的性质，能够逼近任意的非线性函数，并有较快的学习收敛速度，能被广泛应用于各个领域，尤其适用于故障诊断。因此，研究RBF 神经网络在模拟电路故障诊断中的应用有着重要的理论及现实意义[13-14]。

1 基于RBF神经网络的模拟电路故障诊断系统结构

使用RBF 神经网络实现模拟电路故障诊断的一般方法是：①获取样本集，针对电路常见的各种故障状态及正常状态，利用PSpice 工具收集对应的参数值，通过数据预处理，得到RBF 神经网络的学习样本集和检测样本集。②神经网络学习，利用学习样本集对RBF神经网络进行训练，直至网络收敛，获取网络的参数。③神经网络检测，将检测样本集提供给RBF 神经网络，网络输出即为对应的故障模式。基于RBF 神经网络的模拟电路故障诊断系统结构如图1 所示。

2 基本RBF神经网络算法原理

径向基函数（Radial Basis Function）神经网络，简称RBF 神经网络，它用径向基函数作为网络隐含层单元的“基”，隐含层的作用是将低维的模式输入数据变换到高维空间，使得低维空间的线性不可分问题在高维空间线性可分。RBF 神经网络结构上分为三层，即输入层、隐含层和输出层，使用的传输函数（径向基函数）通常有多种，较为常用的是高斯函数。

图1 基于RBF神经网络的模拟电路故障诊断系统流程

其中，wkj(t)为第k 个输出神经元与第j 个隐含层神经元之间在第t 次迭代计算时的调节权重；cji(t)为第j 个隐含层神经元对于第i 个输入神经元在第t 次迭代计算时的中心分量；dji(t)为与中心cji(t)对应的宽度；η为学习因子；E 为RBF 神经网络评价函数，其表达式如下：

RBF 神经网络隐含层神经元的基函数中心C、中心宽度D 以及隐含层到输出层的权值W 是极其重要的组成部分，如果它们选择不当，RBF 神经网络的处理能力将会受到很大的影响，RBF 神经网络训练的目的就是要确定这三个参数。RBF 神经网络的训练通常采用梯度下降法，中心、宽度和权重参数均通过学习来调节到最佳值，迭代计算如下：

上式中，Olk为第l 个样本输入时第k 个输出单元的期望输出值；ylk为第l 个样本输入时第k 个输出单元在的实际输出值。

RBF 神经网络学习算法步骤描述如下：

Step 1:初始化中心、宽度、权重及学习率、动量因子、精度要求等参数。

Step 2:计算网络的隐含层、输出层各单元的输出。

Step 3:计算网络输出的总体误差E 的值。

Step 4:判断结束条件是否满足?满足，则训练结束；否则，转到Step 5。

Step 5:按照式（1-3），对权重、中心和宽度参数进行调整。

Step 6:更新训练次数，返回Step 2。

3 RBF神经网络的改进——一种自适应RBF神经网络算法

RBF 神经网络作为一种前馈神经网络模型，具有较强的泛化推理能力，在诸多领域得到了广泛的应用。但在实际应用中，人们发现RBF 神经网络学习算法的性能在一定程度上依赖于学习率和动量因子的选择。由于基本RBF 神经网络算法中的学习率和动量因子固定不变，给收敛速度带来了一定的影响，对于一些复杂的问题，算法需要较长的训练时间。

为了加快算法的收敛速度，我们对学习率η 和动量因子α 进行自适应调整，提出一种自适应RBF 神经网络算法。该算法的基本思想是：先设定一个初始学习率和动量因子，在学习过程中，根据每次训练后得到的总体误差E（t+1）与上一次训练后得到的总体误差E（t）的大小关系，对学习率和动量因子进行动态调整。如果一次迭代之后误差增大，说明这次调整方向是无效的，应适当减小学习率和动量因子，按原来方向重新计算下一次迭代；如果一次迭代之后误差减小，说明这次调整方向是有效的，应适当增大学习率和动量因子，继续进行下一次迭代。学习率和动量因子的具体调整方法如下：

式中，t=0,1,2,…,T-1,T 为设定的最大学习次数。

自适应RBF 神经网络学习算法的工作流程如图2所示。

图2 自适应RBF神经网络学习算法流程

4 基于自适应RBF神经网络的模拟电路故障诊断实例分析

我们将自适应RBF 神经网络应用于模拟电路故障诊断，本文选择的实验电路是AD 公司提供的电压单端差分转换器，该电路比较简单并具有一定代表性和实用性。

4.1 电压单端差分转换器

电压单端差分转换器电路如图3 所示。

图3 电压单端差分转换器电路

电压单端差分转换器电路中，双通道AD648 是一款低功耗、单片运算放大器，Vcc=10V，Vee=-10V，并对整个电路提供正负电源；V3 为1V 的频率为1kHz 的正弦信号源，R1、R3、R4、R5、R6 分别假设为故障点，在仿真时设置为开路。

4.2 样本数据的获取

我们从PSpice 获取的电路仿真数据集里选取165组数据作为RBF 神经网络的训练样本数据，另选12组数据作为检验样本数据，样本数据覆盖各种故障类型，如表1 和表2 所示。本例设置的故障类型包括无故障（正常）、R1 开路、R3 开路、R4 开路、R5 开路和R6开路，其编码分别为000、001、011、100、101 和110。

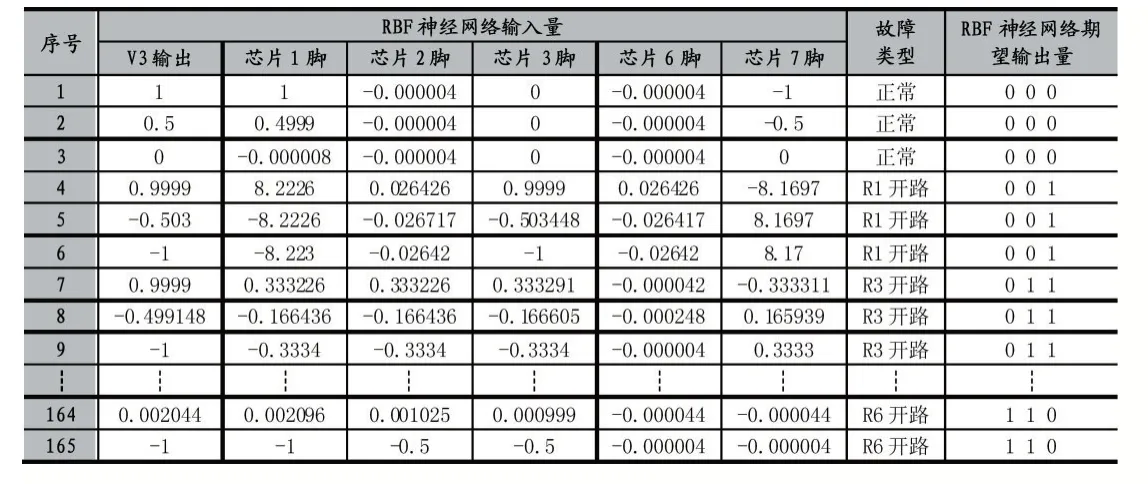
表1 RBF 神经网络训练样本数据

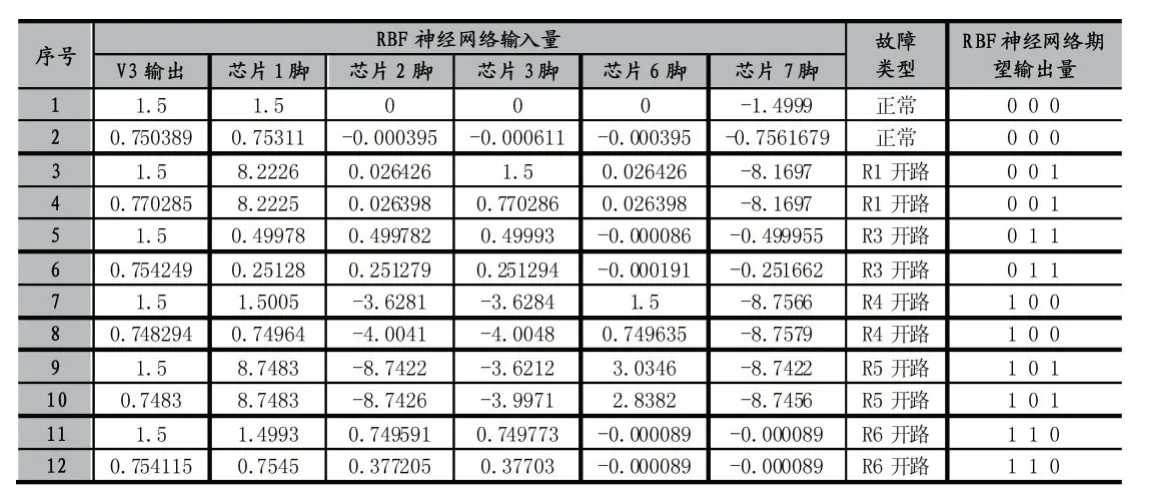
表2 RBF 神经网络检验样本数据

4.3 实验结果及分析

我们首先利用表1 中的数据对自适应RBF 神经网络进行训练，网络结构设置方法如下：6 个测试点对应6 个输入，故障类型采用3 为二进制编码，故输出节点数为3，隐含层节点数按估算公式（7）计算。

其中，nh、ni、no分别为隐含层、输入层、输出层的节点数，np为学习样本个数。根据上述公式求得隐含层节点数为15 个，于是得到网络结构为6-15-3。在给定的训练精度相同的条件下，我们将自适应RBF 神

从表3 和图4 可以看出，自适应RBF 神经网络的平均训练时间比基本RBF 神经网络短，其收敛速度和性能得到了提高。经网络的训练结果与基本RBF 神经网络进行对比，二者的训练时间如表3 所示，收敛曲线分别如图4（a）和图4（b）所示。

表3 RBF 神经网络的训练时间（ms）

当自适应RBF 神经网络训练结束之后，我们再利用表2 中的检验样本数据对网络的泛化性能进行检验，让网络对新的电路故障数据进行诊断，诊断结果如表4 所示。

表4 的诊断结果告诉我们，自适应RBF 神经网络的实际输出与期望输出是完全一致的，也就是说其诊断结果与实际故障类型是完全吻合的。可见，利用自适应RBF 神经网络能够实现对模拟电路故障的准确、可靠的诊断。

5 结语

针对传统的电路故障诊断方法计算复杂，难以适用于现代模拟电路的问题，本文运用神经网络技术，通过建立RBF 神经网络故障诊断模型，实现模拟电路故障诊断。为提高神经网络的训练速度，设计并实现了一种高效的自适应RBF 神经网络算法，将该算法应用于模拟电路故障诊断之中，以电压单端差分转换器电路为例进行了仿真实验。仿真结果表明，该方法具有故障识别速度快、准确性高等优点。今后的工作是将其应用于多故障点的识别，进一步增强算法的适应性，提高算法的性能。

表4 自适应RBF 神经网络的检验结果

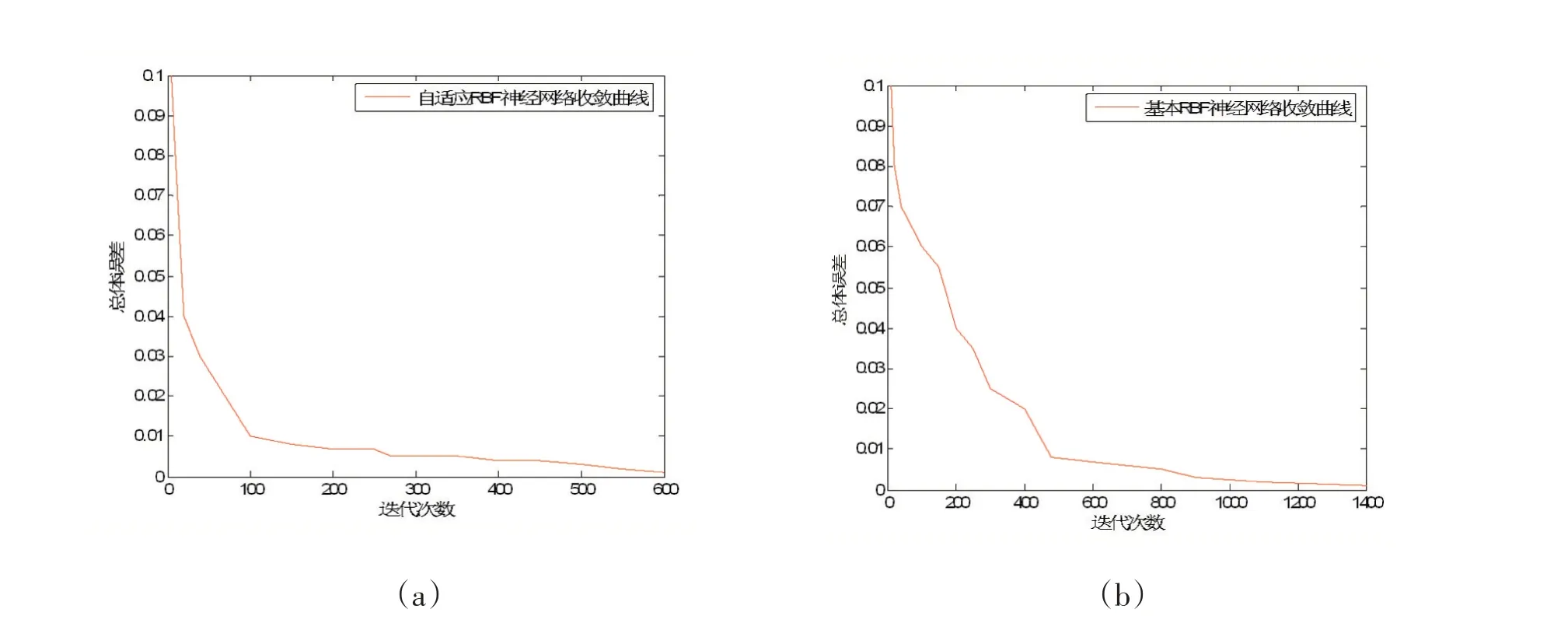
图4 RBF神经网络的收敛曲线