基于双向生长改进的RRT 机器人路径规划算法

李晓伟，于会山

（聊城大学物理科学与信息工程学院，聊城252059）

0 引言

在移动机器人的研究领域中，路径规划算法是最为重要而且不可缺少的组成部分，是移动机器人在障碍物环境下实现自主移动导航的基础。随着路径规划算法研究的不断深入，研究人员已经改善并优化了很多传统的路径规划算法，并不断提出了很多新的路径规划算法，使得路径规划算法的研究趋势已经逐步偏向复杂化和智能化[1]。常用的路径规划算法包括A*、人工势场法、概率路线图（PRM）算法、蚁群算法、遗传算法以及诸多启发式算法等[2]。这些算法的收敛速度过于缓慢，需要提前对未知的障碍物空间环境进行建模，当环境改变时无法在未知的障碍空间中使用。

快速扩展随机树算法由Steven M.LaValle 于1998年首次提出来[3]。RRT（快速探索随机树）算法能有效解决这些传统路径规划算法存在的问题。与其他传统路径规划算法相比，RRT 算法不仅具有快速、高效的特点，而且不需要依赖于环境建模就能够有效地解决未知复杂障碍物空间和高维动态环境的路径规划问题。RRT 是基于空间中树木分支的创建，它迭代地对新的状态进行采样，然后将离每个样本更近的现有节点指向一个新的样本，从而形成一个具有分支的树。即在空间里，从根节点开始，进行任意采样，当采样形成的新点为目标点或新点与目标点的距离小于一定步长时，则形成一条由根节点至目标点的路径[4]。

1 RRT算法

在快速扩展随机树中，qinit为树的根节点（起始点），qgoal为目标点，qrand为任意扩展的随机节点，qnear为每次扩展时距离qrand最近的节点，qnew为新节点[5]。首先在搜索空间中采用随机的方式生成随机树的随机扩展节点qrand，然后遍历当前已有的随机树，从树中的节点里寻找距离qrand最近的节点qnear，在qnear向qrand延伸一定步长之后可以得到新节点qnew，之后需要对新节点进行碰撞检测，若qnew碰到障碍物便把这个节点舍去；反之若qnew没有碰到障碍物，且在规定空间内，即把qnew添加到扩展树中，可知此时qnew的父节点为qnear，按照上述方式继续扩展，直到qnew和qgoal之间的距离小于一定步长时，便规划出了一条由根节点至目标点的路径[6]。基本算法如下所示：

基本的RRT 算法是从根节点开始扩展的RRT 树搜索规定空间。若有两棵随机树，分别从根节点和目标点来搜索状态空间，速度会相对较快。因此，提出一种基于双向扩展的算法，即RRT-connect 算法。

在搜索空间内，定义了两棵随机树。一棵从起始点开始扩展，另一棵从目标点扩展，两棵随机树分别是Ta和Tb，任意选取两随机树Ta和Tb中离qrand最近节点qnear，再从qnear向qrand扩展得到qnew，直到两棵树的qnew小于一定步长，则可确定Ta和Tb连通，即路径规划成功[7]。其算法如下所示：

RRT 算法在采样时，使用启发式采样，即当随机树在扩展时，通过随机概率p1（0≤p1＜1）确定qrand为qgoal的可能性。当目标点就是采样点P（qgoal=qrand）=p1，能够提高RRT 树对目标点扩展的能力，使随机树在生长时更有指向性，树的生长过程会相对收敛。

随机树在扩展新节点时，基本RRT 中qnew的计算如下：

qnew=qnear＋ρ（qrand-qnear）/||qrand-qnear||

ρ 为随机树生长时的步长，（qrand-qnear）表示两向量单位化，||qrand-qnear|||qrand-qnear||为qrand和qnear的欧氏距离。

当把目标引力思想添加到基本RRT 后，qnew的计算如下：

qnew=qnear＋ρ1（qrand-qnear）/||qrand-qnear||+ρ2（qgoal-qnear）/||qgoal-qnear||

ρ1是随机树向任意点方向扩展的步长，ρ2是随机树向目标点方向扩展的步长，为qgoal和qnear的欧氏距离。

基本RRT 算法中的新节点是通过最近节点向随机点延伸一个步长得到的，新节点只朝着随机点生长，可能会偏离目标点，规划出的路径耗时长，距离远。当添加目标引力函数后，qnew也会向qgoal方向生长。当ρ1＞ρ2时，新节点会偏向随机点方向，这就比较接近基本RRT 算法；当ρ1＜ρ2时，新节点会偏向于目标点方向，加快随机树的收敛性。

2 基于双向生长改进的RRT算法

双向RRT 算法尝试扩展两棵树到彼此，相比于基本RRT 提高了算法的收敛速度。不过因基本RRT 在扩展时有一定的随机性，从而导致了双向RRT 无指向性，缺乏稳定性。针对于双向生长具有不稳定的问题，提出一种双向生长改进的路径规划算法[8]。该算法将双向生长和目标引力思想相结合起来。在RRT 双向生长算法中引入目标吸引函数，目标吸引函数使随机树向目标生长。这不仅避免了随机树搜索全局空间，很大程度上降低算法的计算复杂度，提高了实时性，改善了路径的平稳性[9]。

其主要思想是两棵随机树Ta和Tb分别从起始点和目标点开始扩展，若Ta从qinit开始生长，通过随机扩展的方式得到采样点，之后再结合目标引力思想扩展得到新节点。Tb从qgoal开始生长，生长时把Ta扩展得到的新节点当作目标点，采用和Ta相同的方式来扩展。Ta和Tb接下来在生长时都把彼此上一步扩展得到的新节点当成目标点，来进行下一步生长，直到两棵树的距离小于一定步长，即路径规划成功。

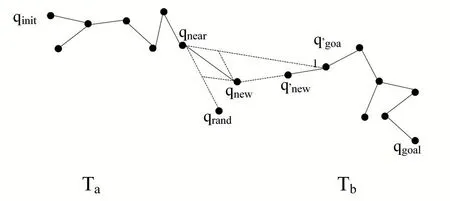
图1 改进RRT构建过程

3 仿真实验

通过用MATLAB 软件来验证文中改进的算法，设置根节点坐标是（0,0），目标点坐标是（490,490）。规划一条由根节点至目标点的有效路径。

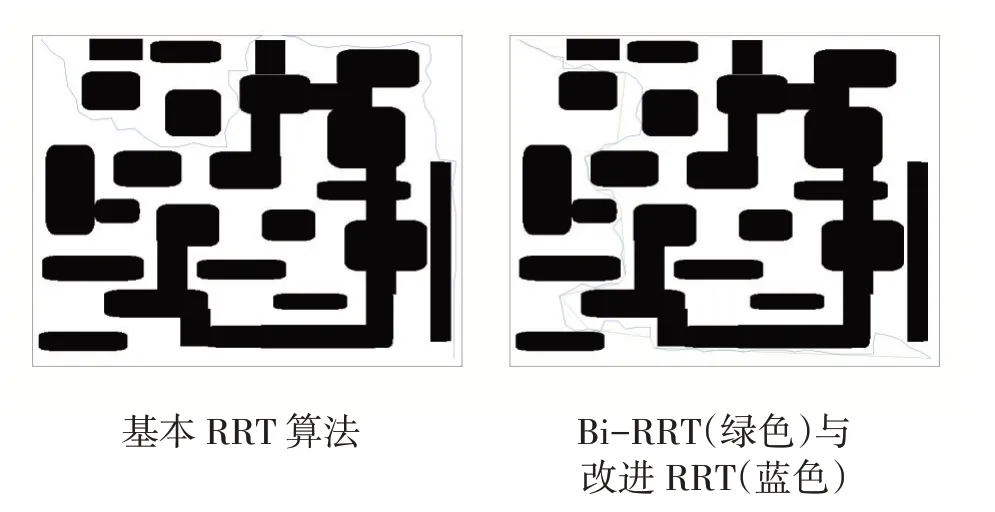
图2

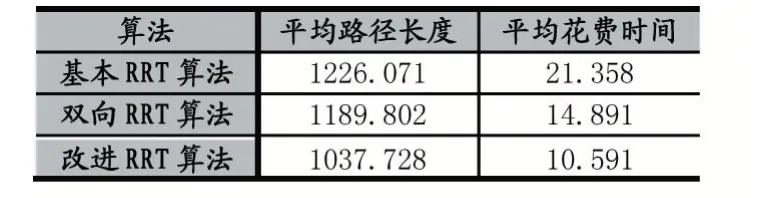
表1

图3

表2

图4

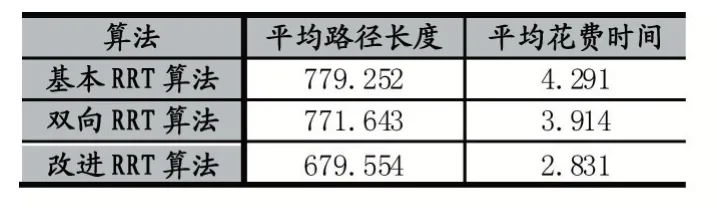
表3

通过在不同环境下进行仿真试验，得到如各表中的实验数据。从而可以得出，相对于基本RRT 算法来说，Bi-RRT 路径规划用时和路径长度更优些。但本文改进之后的算法相比其余两种算法路径更优，运行时间更短，接近最优路径。

4 结语

本文介绍了路径规划的原始算法、双向扩展的方式和加入目标引力思想的双向扩展算法。本文改进的路径规划算法在扩展时减少了路径的随机性，让随机树生长更具有目标性和方向性，但其仍然存在许多不足，例如规划出的路径不平滑，需要进一步进行完善。