轨道交通U形梁对轮轨噪声的遮蔽效应研究

张 迅, 阮灵辉, 曹智扬, 周小刚, 李小珍

(西南交通大学 桥梁工程系,四川 成都 610031)

轨道交通为大众出行提供了便利，但随之而来的噪声问题也颇受非议，特别是在轨道交通的线路形式为高架桥时[1-3]。轮轨噪声是高架轨道交通的主要噪声源之一，为了控制该噪声，目前较为通行的做法是在桥面两侧设置各种高度的声屏障，甚至不惜使用半封闭声屏障和全封闭声屏障[2,4]，如武汉地铁、昆明地铁等。

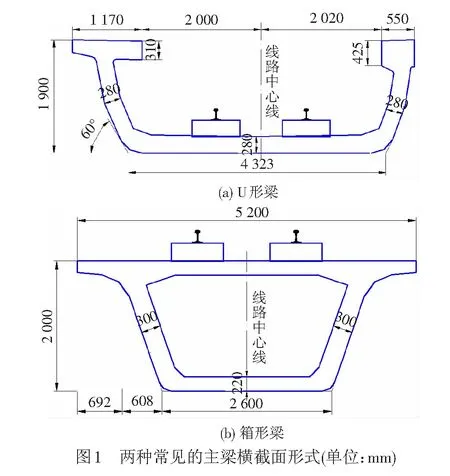
以箱梁为主的传统高架桥，基本为上承式结构，视觉体量大、景观效果差，尤其是在设置声屏障后，庞大的高架桥体量对城市景观的影响更大。因此，工程师们越来越倾向于使用U形梁代替箱形梁(见图1)，因为前者的两侧腹板相当于低矮的声屏障，可以对轮轨噪声的传播起到一定的阻隔作用(本文称之为“遮蔽效应”)[5]。此外，U形梁还具有建筑高度低、断面利用率高、可防止列车脱轨倾覆、外形美观等其他诸多优点。然而，目前有关轮轨噪声的降噪研究大多集中在优化声屏障、设置新型减振轨道等方面[6-8]，而对于U形梁的遮蔽效应研究还极其有限。例如，对于应该如何建模分析U形梁的遮蔽效应、如何定量评价U形梁的遮蔽效应、如何确定影响U形梁降噪效果的主要因素等方面，现有的研究还不够深入。

为定量分析声屏障构造细节对轮轨噪声的降噪效果，现有文献中常采用边界元法进行分析，并取得了非常好的研究成果[9-11]。理论上，边界元法可用于求解具有任意形状的障碍物对声波的传播影响。因此，本文将边界元法引入U形梁对轮轨噪声遮蔽效应的分析中，并定义遮蔽损失这一指标来定量考察U形梁的遮蔽效应。同时，讨论了地面声反射效应和声源的频谱特性对模型计算结果的影响。在此基础上，定量分析了U形梁的上翼缘宽度、腹板高度和腹板倾角对遮蔽损失的影响规律，并给出了相关建议。本文的研究可为轨道交通U形梁的选型及噪声控制提供参考依据。

1 边界元分析方法

1.1 基本理论

二维边界元分析模型见图2，障碍物位于无限大的均匀平面内。计算域D表示上半平面，∂D为计算域边界，S为障碍物的边界，r0为声源点，r为受声点位置。

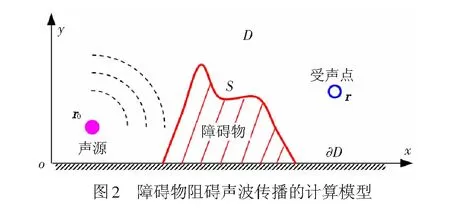
假设空间中传播的声压p随时间按照简谐频率ω变化，即

p(x,y,z,t)=p(x,y,z)ejωt

( 1 )

将式( 1 )代入声学波动方程，可得到某点的声压，并建立Helmholtz方程

2p(x,y,z)+k2p(x,y,z)=0

( 2 )

式中：k为波数,k=ω/c，c为声速；为Laplace算子。

Helmholtz方程的基本解为[12]

( 3 )

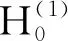
设图2中上半平面的边界(即x轴)具有均匀阻抗边界条件，即常数导纳βc，则上半平面的Green函数记为Gβc。Gβc表示上半平面无障碍物时，Helmholtz方程的解，其表达式为

Gβc(r,r0)=Gf(r,r0)+Gf(r,r′0)+Pβc(r,r0)

( 4 )

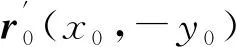
应用Green第二公式可将Helmholtz方程转化为边界积分形式。计算域D内任意点r的声压p(r,r0)计算为

ε(r)p(r,r0)=Gβc(r0,r)+

( 5 )

式中：dS(rs)为障碍物边界S上任意位置rs(xs,ys)的单元长度；∂/∂n(rs)为障碍物边界上的法向导数；β(rs)为障碍物边界上的导纳；ε(r) 为系数，其取决于受声点的位置r，具体计算详见文献[12]。

将障碍物边界S离散为N个线单元Sn(n=1,2,…,N)。记第n个单元的声压为常数p(rn,r0)，rn为第n个单元的中点。积分方程式( 5 )可改写为

ε(r)p(r,r0)=Gβc(r0,r)+

( 6 )

式中：系数C、B分别为单层和双层位势，其计算根据式( 5 )中的对应项确定，可见其与障碍物形状、尺寸等有关。

应用式( 6 )即可求得障碍物表面和计算域其他任意位置的声压。为确保分析精度，障碍物边界的单元划分长度至少应不大于最小计算波长的1/6。

1.2 算法验证

本文利用边界元软件SYSNOISE进行声学分析。为了验证应用边界元法分析遮蔽效应的可行性，先对一简单障碍物(3 m高无限长障碍物)进行分析(见图3)。线声源位于障碍物前方3.5 m处，距地0.5 m高。受声点1#、2#均位于障碍物后方7.5 m处，距地面的高度分别为1.2、3.5 m。

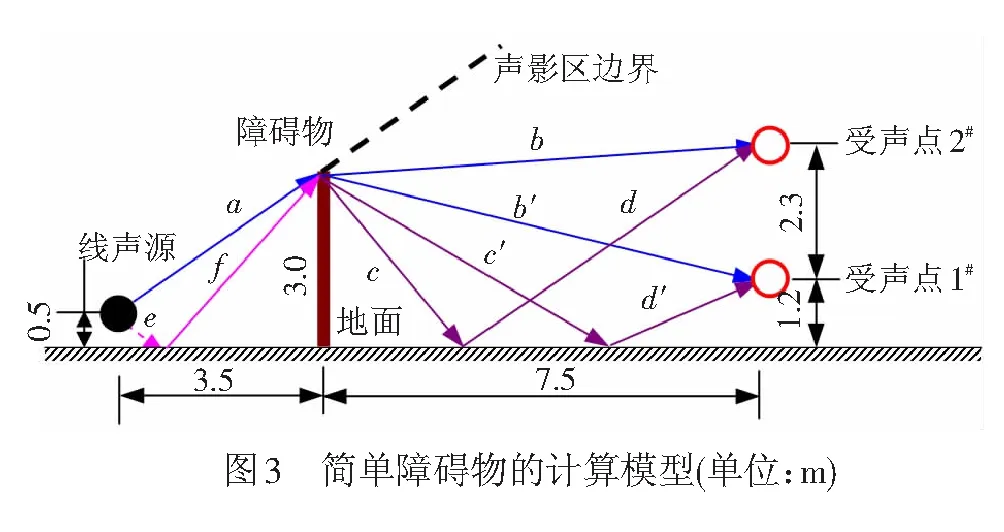
假设地面和障碍物均具有刚性反射面。图3中的虚线示出了声影区边界，可知受声点1#、2#均位于声影区。两个受声点的声传播路径均有4条，不同路径的声波在受声点处相干叠加。受声点1#的传播路径为ab、acd、efb、efcd； 2#受声点的传播路径为ab′、ac′d′、efb′、efc′d′。因此，对于这一简单障碍物问题，可应用几何绕射模型获得解析解。受声点1#、2#的声压解析表达式为[12]

( 7 )

式中：i为传播路径；Ai为声压幅值；φi为绕射引起的相位改变量；di为绕射路径的长度。

声学分析中，通常用插入损失IL描述障碍物对声波传播的影响，即

IL=20lg(pw/o/pw)

( 8 )

式中：pw/o、pw分别为无、有障碍物时的受声点的声压。

在边界元模型中，对障碍物进行网格划分，单元长度取5 mm，满足不大于最小计算波长的1/6的要求。计算频率从20～5 000 Hz、步长为10 Hz。受声点1#、2#的插入损失见图4，由图4可以看出，仿真值与解析值几乎完全一致，仅在个别峰值频率附近略有差别。

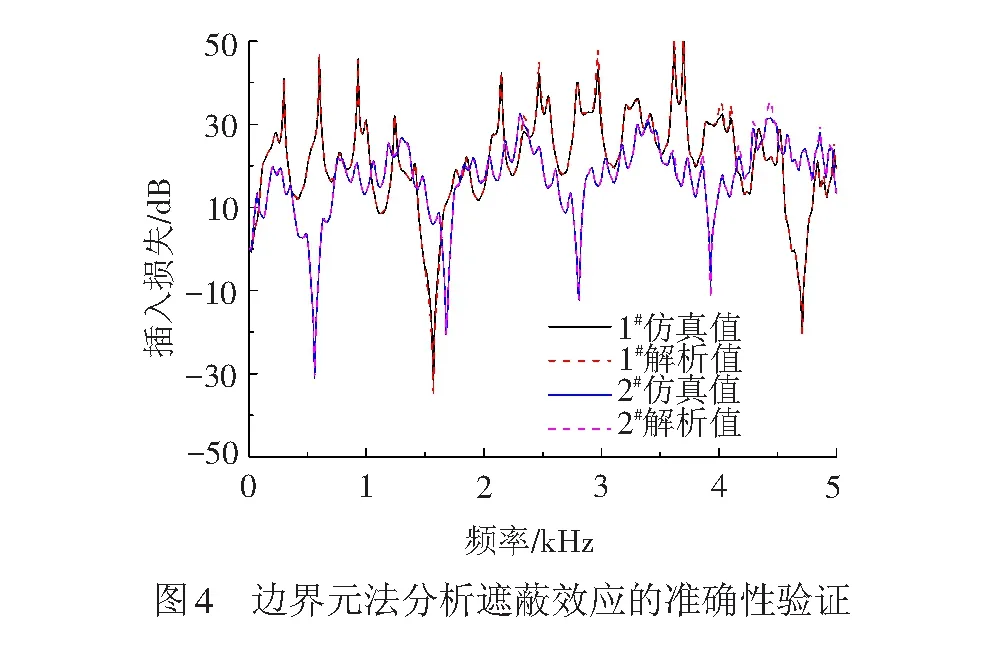
边界元法是基于波动方程的数值解，能够针对任意障碍物形状，计算任意位置受声点的插入损失。该算例验证了边界元法分析遮蔽效应的准确性，因此，可利用该方法对复杂的U形梁引起的遮蔽效应进行分析，而解析解法显然将无能为力。

2 U形梁遮蔽效应的计算模型

2.1 主梁截面尺寸

以图1(a)所示的U形梁为对象进行遮蔽效应研究，并将之与图1(b)所示的箱形梁进行对比。U形梁顶部宽5.74 m，底板宽4.323 m，梁高1.9 m。箱形梁顶板宽5.2 m，底板宽2.6 m，梁高2.0 m。二者均为单线简支梁，跨度30 m，为某实际工程中大量使用的两种梁型。

2.2 边界单元和场点网格

假设桥梁和列车声源沿线路方向不变，建立二维边界元模型进行分析，将U形梁和箱形梁外轮廓划分为线单元，见图5。

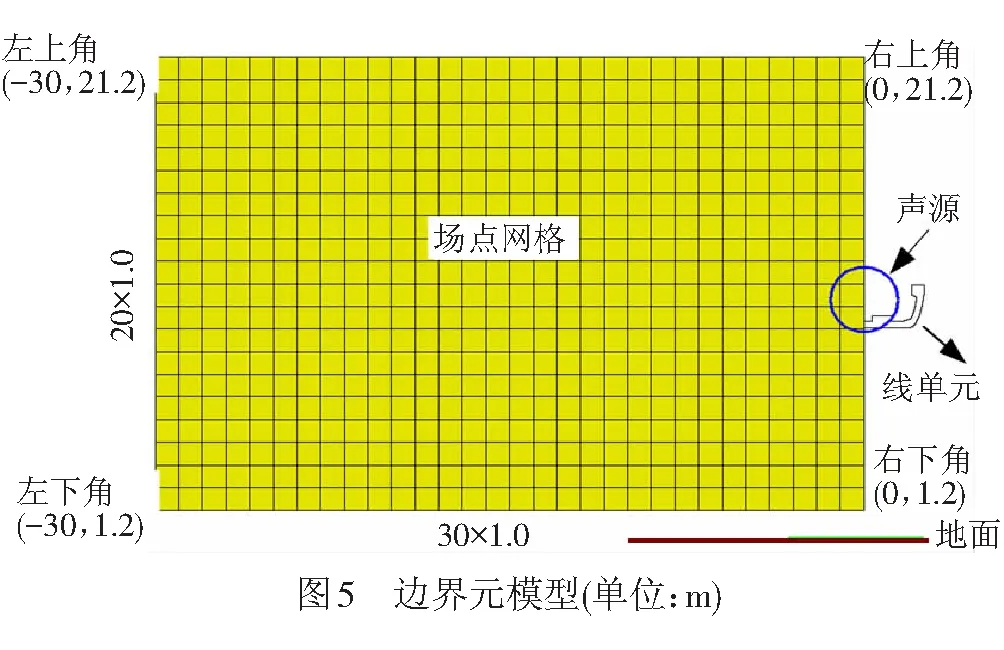
计算频率设为50～5 000 Hz，包含了列车声源的主要频率[14]。为了保证计算精度，边界元模型中的单元尺寸为5 mm。将地面和主梁外轮廓考虑为刚性反射面，即不考虑吸声效果。为具有可比性，两种梁的轨面距地面均为10 m，即保证线路标高不变。空气中的声速取340 m/s，空气密度取1.225 kg/m3。

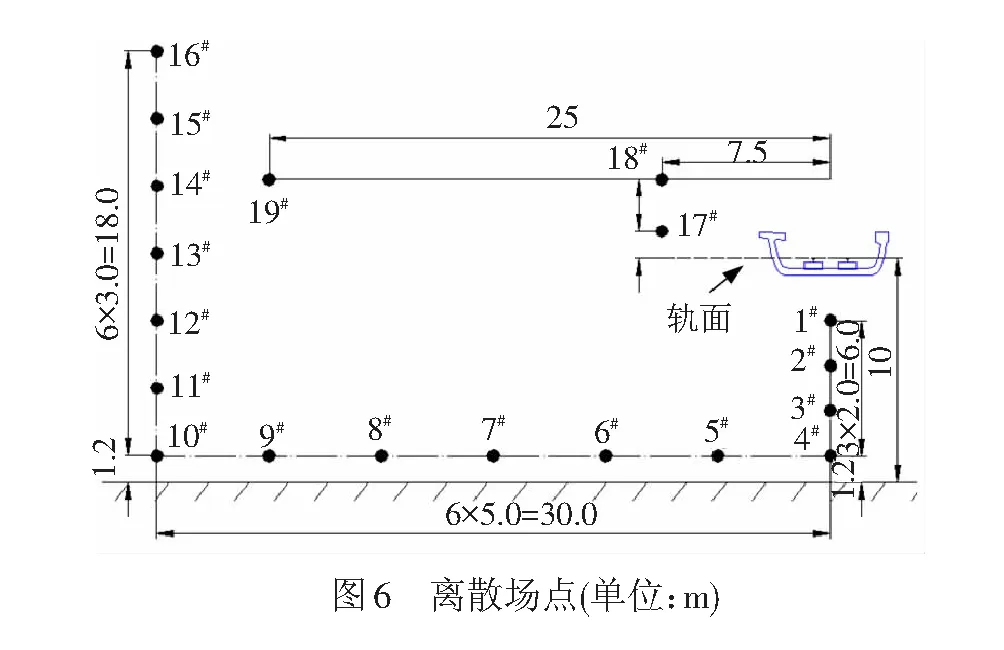
模型中设置30 m × 20 m的场点网格(间距为1.0 m)见图5，以分析梁侧二维声场分布。场点网格在四角的坐标分别为(-30,21.2)、(-30,1.2)、(0,21.2)和(0,1.2)，括号内第一个数字为距线路中心的水平距离，第二个为距地面的竖向高度。同时，结合噪声评价相关要求，定义见图6的19个离散场点。场点1#～4#位于线路正下方，距地面的高度分别为7.2、5.2、3.2、1.2 m；场点4#～10#距地面1.2 m高，横向间距为5 m，其中场点10#为铁路边界噪声控制点；场点10#～16#距线路中心的水平距离为30 m，竖向间距为3 m，代表铁路边界处不同的楼层高度；场点17#～19#为ISO 3095—2005规定的标准场点[15]，坐标分别为(-7.5,11.2)、(-7.5,13.5)、(-25,13.5)，即距轨面的高度分别为1.2、3.5、3.5 m。

2.3 声源选取

文献[14]实测了6节编组地铁A型车以车速69 km/h在高架线上运行时的噪声。测试装置由30个传声器组成一个线形阵列，传声器间距为15 cm，最低处的传声器位于轨面以下0.2 m,最高处的传声器位于轨面以上4.15 m。

截取出列车通过时间内的声压信号，其声功率级和1/3倍频程谱随测试高度的变化曲线见图7。可以发现，声功率级在高度方向上呈现逐步减弱的趋势，最高点和最低点相差约9 dB(A)，并且越接近轮轨噪声辐射位置的量值越大。因此，低速列车以轮轨噪声为主，噪声的主要能量集中在400～1 600 Hz的1/3倍频带内。根据文献[14]的分析，该频带内贡献的噪声能量占79%～85%。

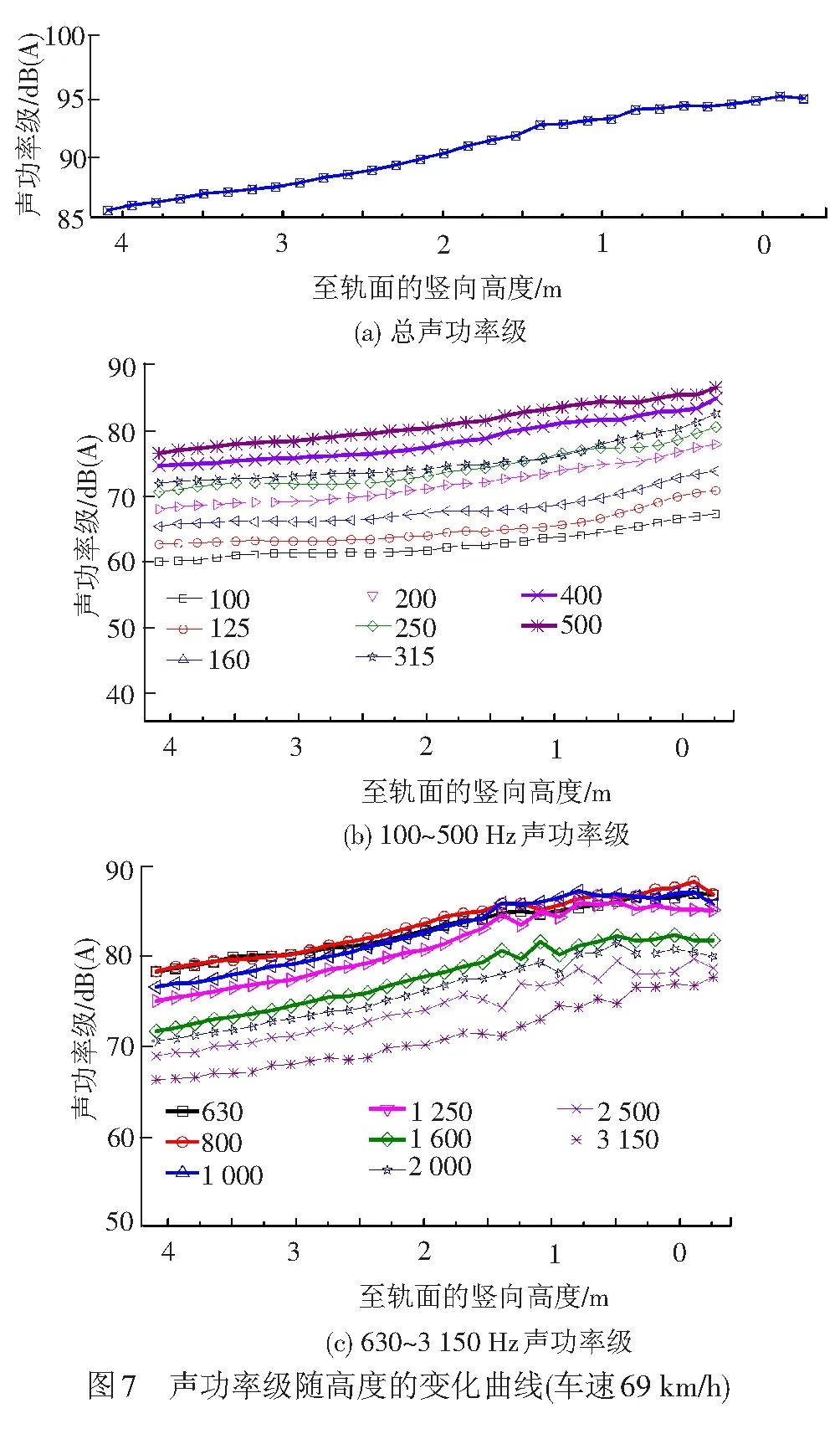
本文的预测模型采用该实测样本作为列车声源输入，以无限长线声源进行模拟，假定其频谱特性在长度方向上不发生变化。

2.4 遮蔽效应的评价

仿照插入损失的定义，本文采用遮蔽损失SL来评价U形梁对轮轨噪声的遮蔽效应，即

SL=20lg(pB/pU)

( 9 )

式中：pB、pU分别为箱形梁和U形梁受声点的声压。根据这一定义，若某受声点的遮蔽损失为正，则U形梁可以起到降噪效果；反之，则起不到降噪效果。

3 影响遮蔽效应的外部因素

影响遮蔽效应的原因很多。本文首先分析地面声反射效应和声源的频谱特性这两个外部因素，因为这是决定模型计算结果的首要因素。

3.1 地面声反射效应

相关文献的研究表明[1，16]，地面声反射对声波传播的影响较大。位于城市中的轨道交通高架线的下方多为坚硬的混凝土地面，对声波能够起到非常好的反射作用。由于列车声源位于梁面以上，桥梁自身就能够在一定程度上阻碍声波的传播，因此，这里的地面声反射效应还有待进一步研究。考虑地面声反射效应时，箱形梁和U形梁的梁侧声压级云图见图8(a)、8(b)。图8(a)所示的箱形梁侧方声场分布与文献[17-18]中的实测噪声变化趋势较吻合，说明该预测模型能够较准确地预测轨道交通高架线附近的声场分布。箱形梁和U形梁均可视为列车声源在空间传播中的障碍物。然而，由于外轮廓形状存在差异，它们对噪声传播的阻碍效果不一致，主要表现在：

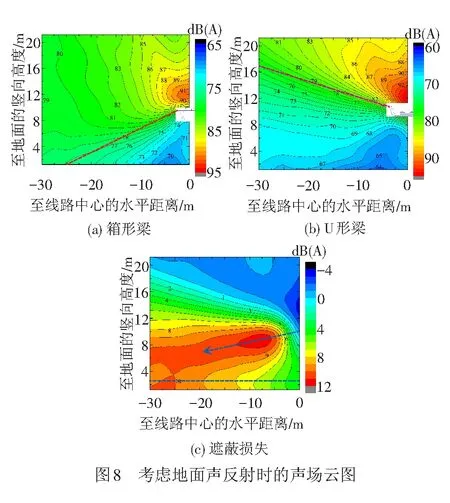
(1) 相比箱形梁，U形梁的腹板和上翼缘使得列车声源更多地被反射到上部空间的一定角度范围内，该范围大致为钢轨与U形梁上翼缘连线形成的夹角区域。

(2) 由于声波在障碍物边缘存在绕射，使得图8(a)和8(b)均出现了声压级等高线密集变化的区域，如图中粗虚线所示。该粗虚线以上范围表示受到列车噪声的影响较大，显而易见，U形梁所对应的范围相对较小。

(3) 对于两种梁型，桥下噪声最小的区域并非位于线路正下方，而是位于地面附近距线路中心5 m附近，这与地面声反射引起的声波干涉有关。总体上，U形梁所对应的噪声较小的范围更大一些。

图8(c)所示的遮蔽损失云图清晰地展示了U形梁的遮蔽效应的有效范围。总体上，除梁面以上一很小的夹角范围外，其他区域均能取得不同的降噪效果。参照轨面所在高度，图中虚箭头所指的方向为遮蔽损失较大的区域(可达10 dB(A))，该虚箭头与竖平面的夹角约为75°。在铁路边界处，即距线路中心30 m处，距地面不高于轨面的位置，遮蔽损失可达8～10 dB(A)。同时，随高度增加，遮蔽效果越来越差；当高度与梁面齐平后，遮蔽效果急剧退化。

不考虑地面声反射时的声场云图见图9。为便于对比，图9与图8中的等值线显示范围保持不变。由图9可以看出，地面声反射仅对靠近地面附近的噪声产生一定的影响，而对其他区域的影响不大；地面声反射使得遮蔽损失等值线有凸向线路外侧的趋势，如图8(c)中粗虚线所示；对于距线路中心30 m以外的区域，地面声反射对遮蔽损失的影响越来越小。

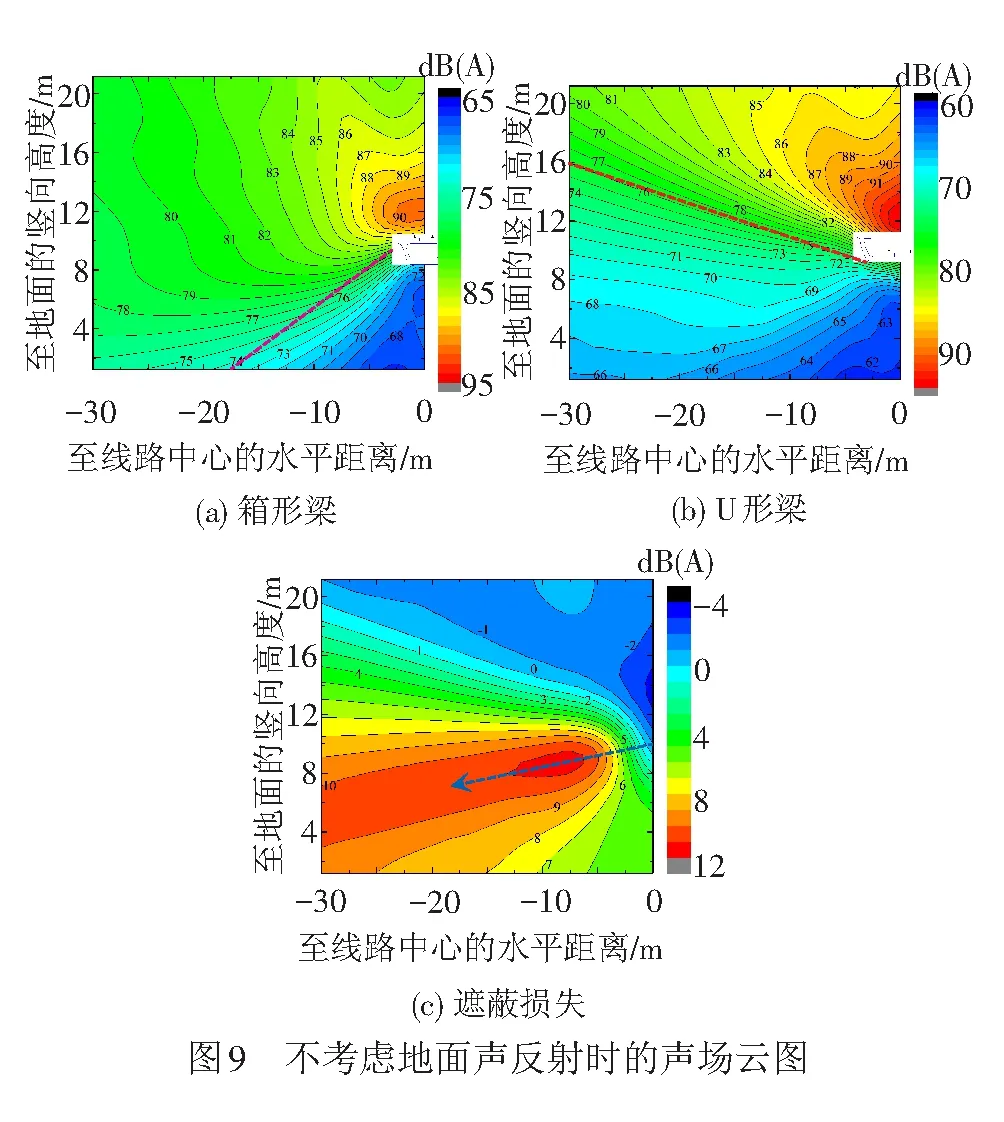
综上所述，就本文所考虑的遮蔽损失指标而言，在轨面距地面10 m高时，地面声反射效应仅对距线路中心约30 m以内且靠近地面附近的区域有一定的影响(在计入地面声反射时，遮蔽损失增大约1 dB(A))，而对其他区域的影响可忽略不计。考虑到实际工程中的桥下地面大多为混凝土路面，因此，在后续分析中均考虑地面声反射效应。

3.2 声源的频谱特性

列车声源的频谱特性受到多种因素的综合影响。本文将粉红噪声源的计算结果与前述实测列车声源的计算结果进行对比，见图10。粉红噪声源为每一个1/3倍频带内均具有相同的声压级(假设为100 dB)，而实际的列车声源能量主要集中在400～1 600 Hz的1/3倍频带内。

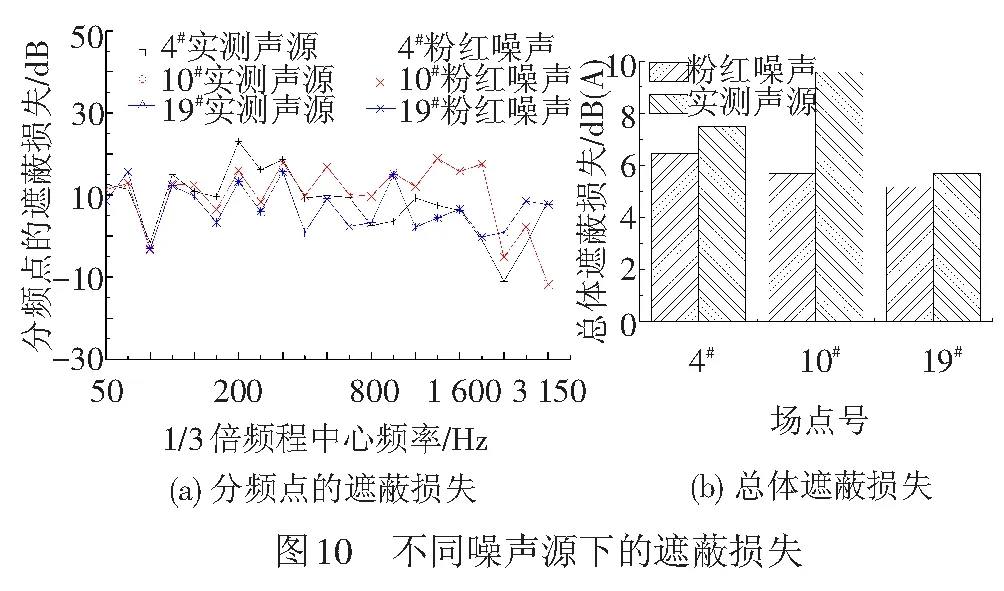
从图10可以看出，不管采用何种声源，场点4#、10#和19#在各分频点的遮蔽损失保持不变，即分频点的遮蔽损失与各频率处的声压级无关，符合一般规律；各分频点的遮蔽损失受到受声点的位置影响，这主要与声程差、声反射有关。

由于假定的粉红噪声源和实测的列车声源差异较大，受声点的总体遮蔽损失并不完全一致，但均表明U形梁可以起到遮蔽效果。针对某一具体工程，应充分考虑车型、车速等因素对列车声源的影响，以得到更准确的遮蔽损失值。另一方面，本文的列车声源为运营线路的实测样本，因此，相关分析结论仍具有一般意义。

4 U形梁横截面尺寸的声学优化

影响U形梁横截面尺寸的因素很多，包括限界、结构构造、静力强度、动力特性等，现从声学角度探讨U形梁横截面尺寸对遮蔽效应的影响。

U形梁横截面分别考虑上翼缘宽度FL、腹板高度WH和腹板倾角WA三个参数，见图11。其中：上翼缘向外侧伸长0.2、0.4、0.6 m时，分别记为FL+0.2、FL+0.4、FL+0.6；上翼缘向内侧伸长0.2 m时，记为FL-0.2(考虑到限界，上翼缘向内侧的伸长量不可过大)；腹板高度降低0.2 m时，记为WH-0.2；腹板高度增加0.2、0.4、0.6 m时，分别记为WH+0.2、WH+0.4、WH+0.6(腹板高度变化不会引起线路高程变化)；腹板倾角减小5°和10°时，记为WA-5°和WA-10°；腹板倾角增加5°和10°时，记为WA+5°和WA+10°。

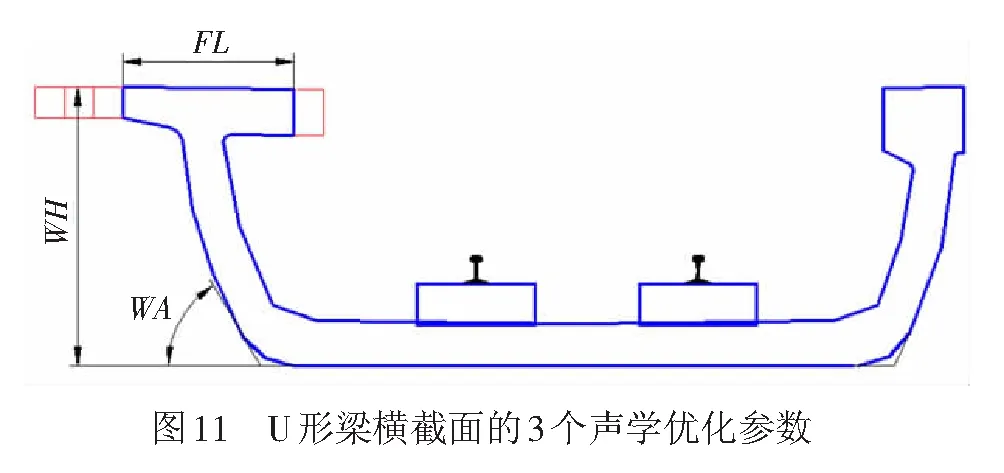
4.1 上翼缘宽度

场点1#～19#的遮蔽损失在上翼缘宽度改变时的变化曲线见图12，其中，遮蔽损失的改变量以原设计上翼缘宽度的遮蔽损失为基准。

从图12可以看出，上翼缘向内、外侧伸长均能对绝大多数场点起到增加遮蔽损失的效果，即降噪效果更好。具体来说：

(1) 上翼缘向内侧伸长时，能够对列车声源(主要是轮轨噪声)起到更好的遮蔽效果，这相当于从源头上对列车声源进行遮蔽。例如，对于铁路边界噪声控制点(场点10#)，上翼缘向内侧伸长0.2 m时，可以使得遮蔽损失增加1.5 dB(A)；对于高度超过梁面的场点，遮蔽损失均有所增加。

(2) 上翼缘向外侧伸长时，相当于增加了声源的绕射路径，故可增加梁面以下场点的遮蔽损失，但只有在上翼缘向外侧伸长的量值足够大时才能使得遮蔽损失取得可观的增加量。由于上翼缘自身就是一个刚性声反射面，因此，这种措施在某种程度上削弱了增加绕射路径所带来的声损失，使得梁面以上测点的降噪效果反而出现降低的趋势(如场点15#～19#)。

(3) 上翼缘向内侧伸长能够起到更好的降噪效果，但考虑到限界问题，上翼缘向内侧伸长的空间并不太多。此时，可考虑在上翼缘内侧粘贴吸声材料，以从源头上进一步增加遮蔽损失。

4.2 腹板高度

场点1#～19#遮蔽损失在腹板高度改变时的变化曲线见图13，其中，遮蔽损失的改变量以原设计腹板高度的遮蔽损失为基准。

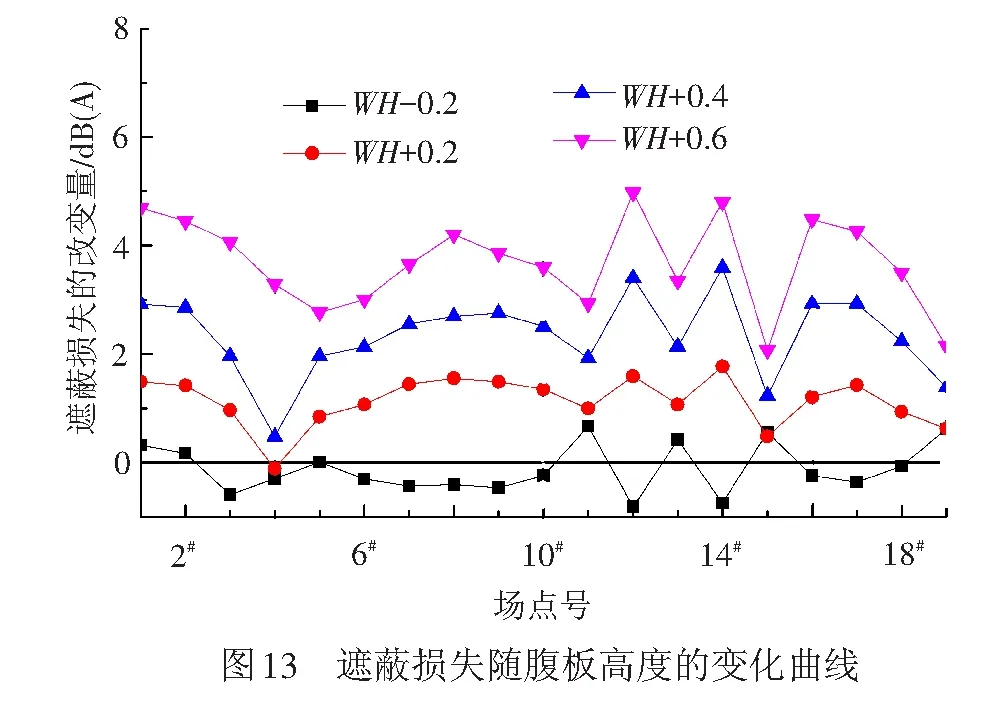
从图13可以看出，腹板高度增大时，遮蔽损失有增大的趋势，而腹板高度减小时，遮蔽损失有降低的趋势。具体来说：

(1) 腹板高度降低0.2 m时，各场点的遮蔽损失降低不明显，例如，对于场点10#～16#(代表铁路边界处不同的楼层高度)，遮蔽损失最多降低0.7 dB(A)。然而，在腹板高度增加0.2 m时，场点10#～16#的遮蔽损失最多增加1.8 dB(A)。这说明从声学角度而言，目前的腹板高度存在一定的优化空间。

(2) 随着腹板高度进一步加大，各场点的遮蔽损失明显增加，即能对轮轨噪声起到更好的遮蔽效果。相对于原设计腹板高度，腹板高度分别增加0.2、0.4、0.6 m时，距线路中心30 m、不同高度位置的场点10#～16#的遮蔽损失平均增加1.2、2.5、3.7 dB(A)，即相当于腹板高度每增加0.2 m，遮蔽损失增加1.2 dB(A)。对于ISO 3095规定的标准场点17#～19#，腹板高度每增加0.2 m，遮蔽损失增加1.1 dB(A)。

(3) 腹板高度增加还可以将更多的高位受声点纳入遮蔽范围，因此，可对空间上更大范围的受声点起到降噪效果。然而，腹板高度增加可能会加大腹板的振动，将会对置于上翼缘的接触网立柱带来危害，实际工程中应充分考虑这一不利影响。

4.3 腹板倾角

场点1#～19#遮蔽损失在腹板倾角改变时的变化曲线见图14，其中，遮蔽损失的改变量以原设计腹板倾角的遮蔽损失为基准。

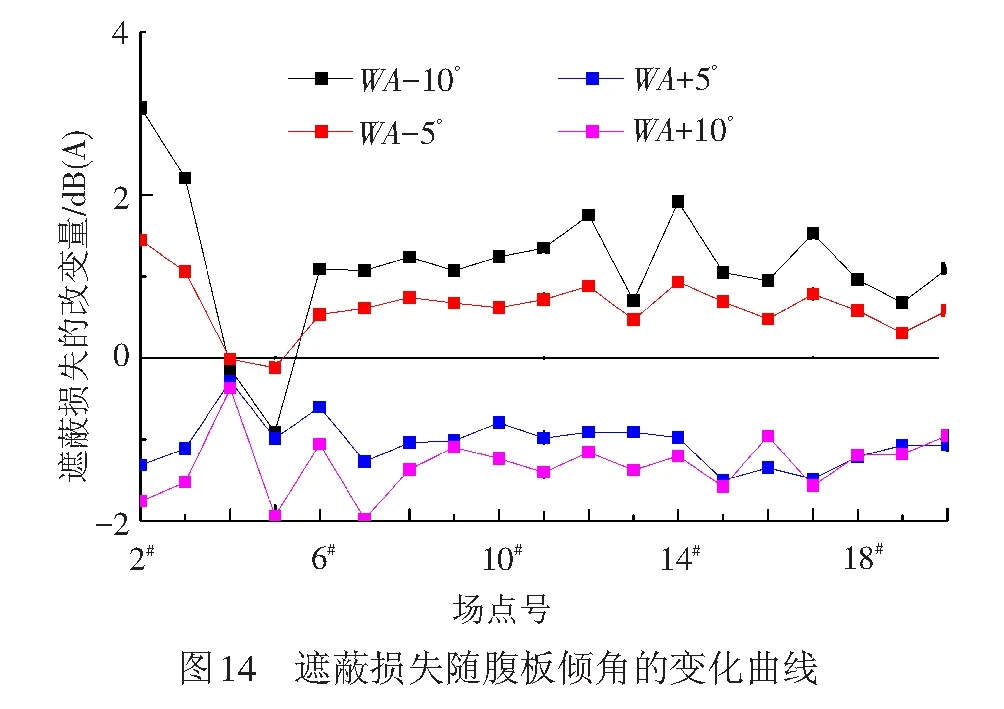
总体上，腹板倾角减小时(向外倾)，各场点的遮蔽损失增大，而腹板倾角增大时(向内倾)，各场点的遮蔽损失增大。对照图12可知，腹板向外倾时，声程差增加，进而使得声损失加大；腹板向内倾时，声程差减小，进而使得声损失减小。

相对于原设计腹板倾角，腹板倾角分别减小5°、10°时，场点10#～16#遮蔽损失平均增加0.7 dB(A)和1.3 dB(A)，而场点17#～19#的遮蔽损失平均增加0.5 dB(A)和0.9 dB(A)；腹板倾角分别增大5°和10°时，场点10#～16#的遮蔽损失平均减小1.2 dB(A)和1.3 dB(A)，而场点17#～19#的遮蔽损失平均增加1.1 dB(A)和1.1 dB(A)。

综合上翼缘宽度、腹板高度和腹板倾角对遮蔽损失的影响可以看出，腹板高度的影响更明显；腹板倾角在改变到一定程度后，其对遮蔽损失的影响越来越弱；上翼缘向外侧伸长时，可能会由于自身的声反射导致轨面以上近场场点的遮蔽损失降低。

5 结论

边界元法能够考虑任意障碍物形状对声波传播的影响。借助该方法，本文就U形梁外轮廓对轮轨噪声的遮蔽效应进行了研究，并将之与箱形梁的计算结果进行对比。主要结论如下：

(1) 分别采用边界元仿真和解析解法就简单障碍物的遮蔽效应进行了探讨，仿真值与解析值几乎完全一致，说明边界元仿真分析进行该类问题的遮蔽效应研究是可行的。

(2) 采用与上述相同的方法，建立二维边界元模型，将U形梁和箱形梁外轮廓划分为线单元；将实测样本作为列车声源输入，以无限长线声源进行模拟，假定其频谱特性在长度方向上不发生变化；将遮蔽损失定义为分别设置箱形梁和U形梁时任意受声点的声级差。仿真分析得到的梁侧声场分布与其它文献中的实测噪声变化趋势比较吻合。

(3) 相对于箱形梁，除梁面以上一很小的夹角范围外，U形梁均能取得不同的降噪效果。参照轨面所在高度，梁侧斜下方75°方向为遮蔽损失较大的区域，最大值可达10 dB(A)以上。距线路中心30 m处，受声点在不高于轨面高程时，遮蔽损失可达8～10 dB(A)。随高度增加，遮蔽效果越来越差；当高度与梁面齐平后，遮蔽效果急剧退化。地面声反射效应对本文定义的遮蔽损失指标影响不大。

(4) 各分频点的遮蔽损失与各频率处声源的声压级无关，但在计算总体遮蔽损失时，声源的频谱特性将产生影响。针对某一具体工程，宜通过现场试验或其它手段获取准确的列车声源样本，以得到更准确的遮蔽损失值。

(5) U形梁的上翼缘向内、外侧伸长时均能起到增加遮蔽损失的效果，但前者更明显，如在上翼缘向内侧伸长0.2 m时，可以使得遮蔽损失增加1.5 dB(A)。如有条件，可在增加上翼缘内侧宽度的同时，在内侧粘贴吸声材料，以进一步增加遮蔽损失。

(6) U形梁的腹板高度增加时，遮蔽损失明显增大，并可将更多的高位受声点纳入遮蔽范围。对于铁路边界不同高度处，腹板高度每增加0.2 m，遮蔽损失增加1.2 dB(A)。

(7) U形梁的腹板向外倾时，遮蔽损失有增大的趋势，而腹板向内倾时，遮蔽损失有减小的趋势。对于铁路边界不同高度处，腹板外倾10°时，遮蔽损失增加1.3 dB(A)。

针对某一具体工程，影响遮蔽损失的因素可能更复杂，但仍可以借鉴本文的建模方法进行分析。同时，声学优化设计应与常规结构设计同步进行，以确保结构承载力。