基于放疗的六自由度医用机械臂动力学仿真分析

陈继朋，陈惠贤，杨小龙，刘晓娟，乔宇，马利强

1. 兰州理工大学 机电工程学院，甘肃 兰州 730050；2. 晋中学院 机械学院，山西 晋中 030600

引言

医用机械臂的任务是在放疗过程中承载肿瘤患者，并以等中心点为目标对肿瘤治疗靶区进行放疗前期的摆位和放疗过程中的位姿调整。与传统治疗床相比较，医用机械臂具有灵活性高、工作范围大等优点[1]。由于肿瘤区域形状多为复杂曲面，即医用机械臂末端轨迹为不连续的直线或者弧线，这对机械臂的运动轨迹精度提出了更高的要求，要求医用机械臂走出沿肿瘤区域形状的复杂轨迹[2-3]。减少机械臂的运动误差，提高计划靶区（Planning Target Volume，PTV）与放疗靶区（Radiotherapy Target Volume，CTV）之间的重合度，进而提高放疗精度。已有研究对床板末端旋转关节搭载力矩传感器，根据牛顿-欧拉方程建立末端动力学方程，对运动位移误差进行补偿[4-7]。对医用机械臂动力学研究可以解决机械臂系统的控制问题，实现预期轨迹运动和动态性能，同时为医用机械臂的最优化设计提供理论基础[8-11]。在提升放疗精度方面，肿瘤患者的摆位、图像引导（Image Guide Radiotherapy，IGRT）、医用加速器放疗剂量控制等方面对放疗精度都有不同程度的影响[12-17]。其中对肿瘤位置精度影响最大、研究成本较低的是医用机械臂。

本文针对肿瘤患者载荷大负载特性，基于ADMAS 软件对虚拟样机进行了仿真，分析了患者重心位置变化对医用机械臂的动力学影响。研究结果为后期医用机械臂运动控制和位置补偿提供依据，以提高医用机械臂的运动及动力学性能，为肿瘤精准放疗提供保证。医用机械臂的结构简图如图1 所示。

图1 医用机械臂的结构简图

1 医用机械臂模型及治疗环境

考虑精准放疗所需的设备相关性能要求和约束条件，本团队自主设计了面向重离子精准放疗的医用机械臂，同时医用机械臂及治疗环境下的模拟示意图如图2 所示。

图2 医用机械臂

2 医用机械臂的运动学分析

2.1 基于MATLAB/robotic toolbox 机器人工具箱的建模

创建机器人的两个最重要的函数是：Link 和SerialLink。对其中Link 函数的参数作简单介绍：theta 为关节角度；d 为连杆偏移量；a 为连杆长度；alpha 为连杆扭角；sigma 表示旋转关节为0，移动关节为1；mdh 标准的D&H 为0，否则为1；offset 表示关节变量偏移量；isprismatic 测试是否为移动关节。医用机械臂的D-H 参数，见表1。为了减少运算量，将整体结构缩小十倍，通过相关函数可以建立医用机械臂的简化模型。医用机械臂的MATLAB 模型及编程部分程序，见图3。

表1 医用机械臂的D-H参数

图3 医用机械臂的MATLAB模型及编程部分程序

2.2 医用机械臂的轨迹规划

轨迹规划既可以在笛卡尔空间坐标系下进行，也可以在关节空间坐标系进行。关节空间的轨迹规划是以关节角度的函数来描述医用机械臂轨迹的，也就是说医用机械臂末端执行器的运动轨迹是由关节变量直接确定的。在笛卡尔空间坐标系中，直接设定末端执行器的始末位置，进而求得各关节角度的关节角位移。

本文针对肿瘤患者放疗结束后，医用机械臂从摆位位置运动到停止工作的位置进行研究。数值仿真模型仿真起点坐标为（270，0，113.8），仿真终点坐标为（170，-100，73.8）。在满足医用机械臂行程范围且与其他设备没有干涉的要求下选择一条行程最短、能量消耗最小和机械臂空间变换最少的路径。根据设计参数，移动关节的最大速度为v=75 mm/s。考虑到已经将整体结构在MATLAB 中缩小十倍，故将速度等比例缩小。将v=75 mm/s 带入MATLAB 仿真程序，假设整个过程运行位移为S。

取仿真时间为20 s，为了将仿真轨迹尽量平滑，将仿真步数设置为step=50，得到医用机械臂末端轨迹如图4 所示。

图4 医用机械臂末端运行轨迹

2.3 MATLAB逆向运动求解

图4 所示为医用机械臂的末端运行轨迹，调用robotic toolbox 中求逆函数ikine。

T1=transl(270,0,113.8)；

T2=transl(170,100,73.8)；t=50；

T=ctraj(T1,T2,t)；

Q=robot.ikine(T)。

函数进行机器人的轨迹规划，其中T1 为末端执行器的初始值，T2 为末端执行器的终点值，t 为采样步数，即得到各关节角度的变化量。打开MATLAB 左下方的工作栏，找到各个关节角度变量保存为txt 文本。截取其中关节1、2、3 的位移变化曲线如图5 所示。

图5 部分关位移仿真步数变化曲线

3 基于ADAMS的动力学分析

3.1 医用机械臂的动力学模型

目前，机器人动力学的研究方法很多，如拉格朗日方法、牛顿-欧拉方法、高斯方法、凯恩方法、罗伯逊-魏登堡法、旋量方法等。其中以牛顿-欧拉法和拉格朗日法运用较多。从计算量方面考虑，使用牛顿-欧拉方法，将所有杆件的速度、加速度、惯性矩阵、质心位置、力和力矩等都表示在各杆的坐标系中，从而使计算更加简单，使计算关节驱动力矩的时间不仅与机器人关节数成线性比例，而且与医用机械臂的构型无关。

首先从连杆1 到连杆n 向外递推计算各连杆的速度和加速度，计算出每个连杆的惯性力和力矩。第二步，从连杆n 到连杆1 向内递推计算各连杆内部相互作用力和力矩、关节驱动力和力矩，见图6。其中，xi、yi、zi分别代表第i 个关节的三个方向坐标。mig 代表第i 个连杆的重力，ni作用于连杆i 质心上的力矩，ipi+1 为i 连杆的质心位置，rci为i 连杆质心相对关节i的旋转半径，Oi为关节i的坐标中心，fi作用于连杆i质心上的力。

图6 连杆受力分析

（1）向外递推（i：0 →n-1）。

连杆i+1 的角速度：

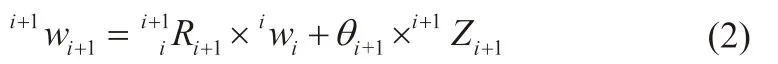
连杆i+1 的角加速度：

连杆i+1 的线速度：

连杆i+1 的线加速度：

作用于连杆i+1 质心上的力：

作用于连杆i+1 质心上的力矩：

（2）向内递推（i：0 →1）。

作用于连杆i 质心上的力：

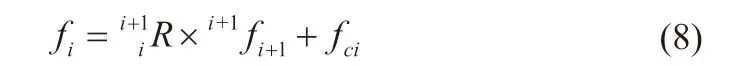
作用于连杆i 质心上的力矩：

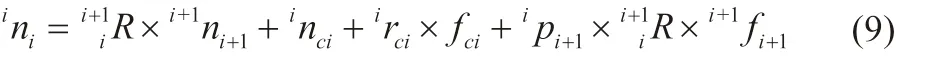
关节驱动力矩：

建立好机器人动力学模型，可以在已知各关节位移、速度和加速度的情况下，求得各关节所需要的驱动力和力矩，为机器人的动力学仿真提供依据。

3.2 关节刚度模型

线性弹性系统关节的力变形关系：

其中，f 参数为6×1 的关节所受的外力或者力矩，Kx参数为6×6 的刚度矩阵，参数为6×1 位移偏差或者转角偏差。假定机械臂连杆为刚体，关节在旋转方向上为弹性体，关节径向方向刚度很大。

在笛卡尔空间坐标系下变形产生的能量跟关节坐标系下产生的能量相等，根据虚功原理：

根据雅可比矩阵的定义，

把公式(13)带入公式(12)可得：

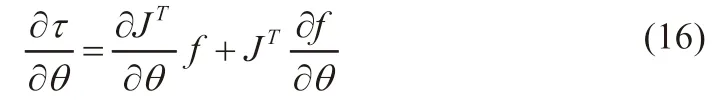
把式(10)和式(11)带入式(16)可得：

Kc为机器人结构变形刚度，综上所得

同理可得：

3.3 医用机械臂的动力学仿真分析

3.3.1 驱动函数的设置和末端载荷的施加

对SolidWorks 中的医用机械臂三维模型中关键零部件进行结构简化，把没有相对运动的零件组合成组件，另存为Parasolid (x_t)格式导入ADAMS 中。在ADAMS 中重新定义各零部件的材料属性，采用轻质铝合金，确定密度、弹性模量、刚度等参数。在关节模型处添加运动副、固定副、maker 点，得到医用机械臂的动力学模型。利用前一章中Robotics Toolbox 轨迹规划得到的各关节角位移，在MATLAB 中已经将各杆件长度缩小十倍，故应将移动关节变化数值放大十倍，转动关节角度数值不变。在ADAMS中通过Data Elements 功能建立各关节样条曲线SPLINE，对应的驱动函数调用格式为CUBSPL ( time, 0, SPLINE_number, 0)，最后将六个关节样条驱动函数依次施加到相应的运动副上。其中关节1 的样条曲线如图7 所示。

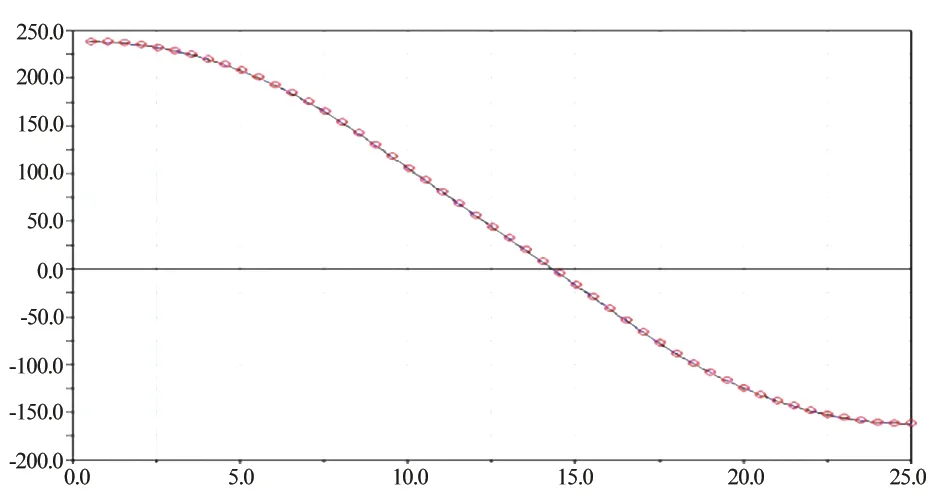
图7 关节1的spline函数

参考中国正常人的标准体重表，假定肿瘤患者体重为1000 N。考虑到肿瘤患者的重心位置的不同，在医用机械臂床板中心建立一个薄圆槽，沿着床板x 方向距离圆槽两侧距离60 cm 和40 cm 处分别建立两个圆槽，方便建立marker 点，床板上从左到右的依次为marker9、marker10和marker11。模拟肿瘤患者重心位置。针对其中任意一个marker 点施加恒定载荷1000 N，仿真时间设为20 s，采样步长设为0.04 s。选取末端床板质量中心点作为标记点，记录各关节的位移、速度、加速度变化曲线，各关节中心的位移变化曲线如图8 和图9 所示。分析对比不同marker 点施加1000 N 时末端床板的位移变化曲线。

图8 ADAMS中医用机械臂上的三个圆孔槽

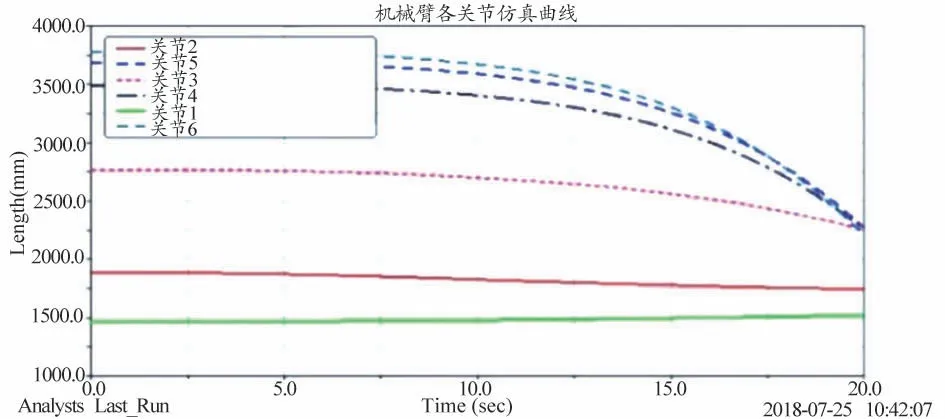
图9 医用机械臂各个关节的位移仿真曲线

从仿真结果可知，各关节位移变化曲线都比较平缓，没有出现陡峰和拐点。轨迹规划中，医用机械臂首先进行水平面的转动，然后才有竖直方向的移动。在5～10 s 运动期间，大臂、小臂及末端床板的位移变化明显；运动时间在15～20 s 之间，位移变化较为明显。

3.3.2 末端质心位移偏差

仅列出对末端marker11 点施加1000 N 时医用机械臂仿真轨迹中位移、速度、加速度的变化曲线，其曲线分别对应图10 a、b 和c。

图10 Marker11点加载的位移、速度、加速度曲线

由图10 b 和c 可知，医用机械臂在整个运动过程中末端速度、加速度变化平缓，没有突变，且都符合技术规范中对速度、加速度的要求。在ADAMS 中空载运行前一章得到MATLAB 仿真轨迹，分别记录末端床板在0、2.5、5、10、15、20 s 时的x、y、z 方向的位移，与之前marker9、marker10、marker11 三点施加1000 N 时末端床板的位移曲线进行对比。

从表3～5 可知，在仿真刚开始阶段位移偏差几乎为0，在仿真10～20 s 内，位移偏差逐渐增大。Marker9 点y 方向的最大位移误差为2.078 mm，在x 方向和z 方向的最大位移误差0.82 mm 和1.07 mm。marker11 点在y 方向的最大位移误差1.889 mm，在x 方向和z 方向最大位移误差0.81 mm和0.97 mm。在y 方向的位移偏差比x、z 方向的位移偏差都大，这与患者的重心方向相重合的原因相吻合，对x 方向的位移偏差影响最小。随着运行时间的增加，运动误差有增大的趋势。

表3 Marker9点的位移偏差表

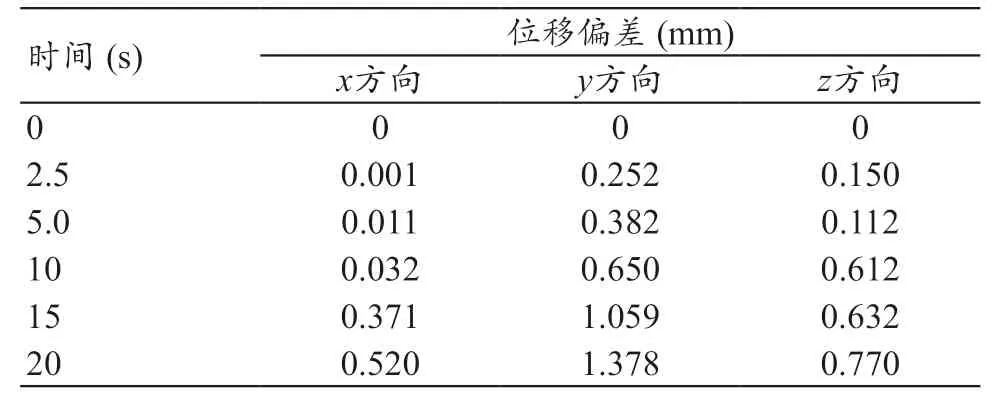
表4 Marker10点的位移偏差表

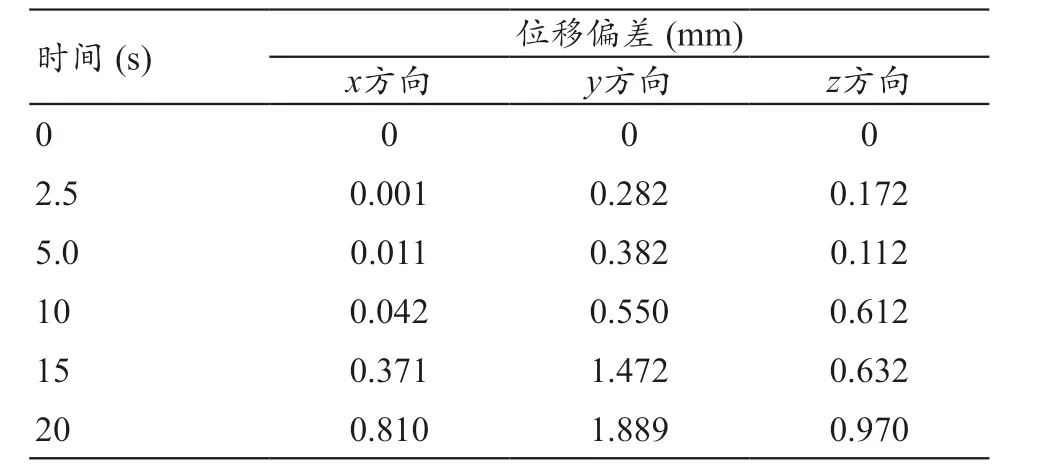
表5 Marker11点的位移偏差表

Marker9 比marker11 离床板末端位置中心更远，marker9 加载下产生的最大位移误差更大。位移误差会累积传送到肿瘤位置区域，为医用机械臂的运动补偿提供定量分析。

3.3.3 各关节扭矩曲线仿真

这里仅列出marker10 和marker11 点加载下的力矩曲线图，见图11。从图11 可知在y 方向的最大力矩大于在x 和z 方向的最大力矩。Marker11 点加载下的力矩在大于marker10 点加载下的力矩。在摆位过程中，应该尽量将肿瘤患者摆放在床板等中心点，提高放疗精度。

图11 不同加载点的力矩曲线

4 结论

本文基于医用机械臂特定轨迹，结合机器人运动学、动力学仿真常用的三个软件SolidWorks、MATLAB 和ADAMS，运用联合仿真的方法，对医用机械臂刚体多体医用机械臂动力学模型，并进行运动学、动力学仿真分析，验证了肿瘤患者在床板位置中心不同存在位移偏差，得到了医用机械臂末端位移偏差曲线和力矩曲线，为RV 减速器的选型和医用机械臂的运动补偿提供依据。这种联合分析的方法，结合了SolidWorks 强大的绘图、MATLAB 的运动学分析以及ADAMS 的动力学分析的优势，克服了单独使用的局限性，提高了在加载状态下医用机械臂动态响应的准确性。精准的模拟了医用机械臂的运动状态，为医用机械臂的运动控制和位移补偿提供了理论依据。