大型海上风电机组扭振瞬态响应计算研究
刘 欢 , 周瑞平, 廖鹏飞
(1.武汉理工大学 能源与动力工程学院,湖北 武汉 430063;2.江西江铃集团 新能源汽车有限公司,江西 南昌 330013)
0 引言
目前,风力发电机组已呈现大型化、低速化的趋势,直驱型风力发电机组以其故障率低、可靠性高,越来越多地受到海上风电行业的重视,传统的静态设计很难满足风电传动高可靠性要求。由于风能具有明显的随机性、波动性、间歇性等特点,这种不稳定的载荷容易使风电机组传动系统产生扭振,进而造成了风电机组的各部件的故障甚至破坏,降低了风电机组的发电质量和传动系统的使用寿命,增加了风场的运营和维护成本[1-2]。
国内外学者对风电机组传动系统的扭振瞬态响应的研究较少,大部分仅针对风电机组传动系统中单个部件(如叶片、齿轮箱、偏航系统、塔筒等)进行扭振分析,或者针对传动系统仅考虑恒定载荷下的扭振响应,未考虑风的动态载荷对系统扭振的影响[3-4]。因此,建立适合我国海上直驱型风力发电机组瞬态动力学计算分析流程,对我国风力发电机组机械设计理论发展具有重要意义。
本文以海上直驱型风电机组传动系统为研究对象,建立了基于风剪切-塔影-湍流效应的随机风载荷模型和风电机组传动系统的扭振简化计算模型;采用Newmark-β[4]逐步积分法得到了传动系统的瞬态扭振响应,形成了完整的风电机组传动系统扭振计算与校核的流程。通过对上述关键技术的研究分析,可实现我国大规模海上风电开发和海上风电场建设的需要,保障海上风电的健康可持续发展,同时对提高我国风力发电制造企业自主研发与设计能力具有重大意义。
1 建模方法研究
海上直驱型风电机组主要由风轮、传动轴、发电机和机舱等构成。对该系统进行扭转振动特性分析时,在满足工程精度要求的前提下,为提高计算效率,降低计算成本,需对系统进行一定程度的简化。在进行扭振分析时,模型简化的方式很多,但都应遵循以下基本原则:(1)系统的总惯量不变;(2)模型的固有频率与原系统的固有频率一致。
目前,轴系扭振的集总参数法已较为成熟,被广泛用于各类旋转机械的扭振分析。常用于风力发电组系统的简化模型有六质量块模型、三质量块模型以及二质量块模型,其中六质量块和三质量块模型一般被用于带齿轮箱的风电机组的建模。针对海上直驱型风电机组传动系统的扭振计算,本文建立了基于集总参数法的二质量块模型,即将叶片与桨毂简化为第1个质量点,发电机转子作为第2个质量点,简化后的模型见图1。图1中,J1、J2分别为质量点1和质量点2的惯量;c1、c2分别为两个质量块的阻尼;θ1、θ2分别为两个质量块的转角;k12为两质量点间的刚度;c12为两质量点间的阻尼;M(t)为施加在质量点1处的扭矩。

图1 海上直驱型风电机组的二质量块模型
2 瞬态扭转振动计算的关键技术
一般地,n自由度系统的扭转振动微分方程见式(1)。

(1)
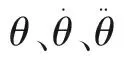
风电机组传动系统瞬态扭振计算的影响因素主要包括:惯量、刚度、阻尼、气动载荷及电机扭矩特性等,其中惯量、刚度、阻尼等系统参数由厂家提供。
永磁直驱型风电机组大部分情况下在额定风速以下运行,为了捕获最大风能,运行时一般采用变速恒频发电的工作方式。变速恒频发电运行方式为:机组在额定风速以下时,风电机组按最优桨距角定桨距运行,以达到最佳功率曲线追踪和最大风能的捕获;在额定风速以上时,由风力机控制系统通过调节桨距改变风能系数,从而控制风电机组的转速和功率。因此,在不考虑电网波动对机组的影响时,可近似认为发电机的外部激励力矩为0。
综上所述,在进行扭振响应计算时仅需考虑风载荷对系统的影响。根据上述条件,可得出永磁直驱型风电机组的扭振微分方程,见式(2)。
(2)
图2为海上直驱型风电机组传动系统扭振计算分析流程。本文主要研究不同气动载荷模型对海上大型风电机组扭振特性的影响。
3 风载荷计算模型
由于风剪切效应和塔影效应的存在,风速值在整个风轮扫掠面上处处不同,从而导致了在风轮扫掠面上所受到的空气动力扭转载荷的变化。此外,由于风速本身的随机性,也会造成激励力矩的变化。常被用于风电机组载荷计算与分析的风速模型主要有:风剪切模型、塔影效应模型和湍流风速模型。

图2 风电机组扭转振动计算分析流程
3.1 风剪切模型
对风剪切的计算常采用指数模型,即:

W(r,φ)]
(3)
式中:V(z)为离地高度为z处的风速;Vh为轮毂处风速;h为桨毂处高度;z为离地垂直高度;α为风剪切系数;φ为方位角。
3.2 塔影效应模型
塔影效应模型的表达式为:
V(y,x)=Vh+Vt(y,x)
(4)
(5)
式中:V0为空间平均风速;a为塔架半径;y为桨叶微元到塔架轴线的y轴方向距离;x为桨叶微元到塔架轴线x轴方向距离,即悬垂距离;Vt(y,x)为塔影效应对风速施加的变化扰动。
3.3 风剪切-塔影效应模型
风剪切和塔影效应中使用的是不同的参考风速。风剪切使用的是桨毂离地高度处风速Vh,塔影效应中使用的是空间平均风速V0,二者有如下关系:
(6)
式中:R为全桨叶半径。
(7)
由于y=rsinφ,式(5)可改写成下式:
=Vhvtt(r,φ,x)
(8)
式中
(9)
需要注意的是,塔影效应只产生于下半叶轮扫掠面,即方位角0.5π≤φ<1.5π。风电机组桨叶微元到叶轮中心距离r的范围由式(10)确定:
0 (10) 根据叶片微元半径距离r和方位角β的不同取值,可得到4个区域风速计算模型。其区域划分见图3。 图3 作用于风电机组的风速区域划分 区域①风速计算模型: (11) 区域②风速计算模型: (12) 区域③风速计算模型: (13) 区域④风速计算模型: (14) 湍流风速具有随机性强的特点,其各频率下的能量分布可以用各向功率谱密度函数描述。根据风电机组设计要求IEC 61400—1标准最新版推荐的Kaimal湍流谱模型进行计算,其风速谱计算公式为: (15) 式中:f为频率;k为3个分量方向;Sk为单方向的风速谱;σk为湍流标准偏差;Lk为尺度参数;v为风电机组轮毂高度的来流风速。 在实际建模计算中,需将Kaimal风速谱转化为时域风速函数: (16) 式中:w=2πf;t=i·Δt;i=1,2,3,…,N;ψn为方位角,取0到2π之间的值;T为阵风特性时间。 根据贝兹理论,风电机组的转矩可近似由式(17)表示: (17) 式中:λ为风机叶尖速比;ρ为空气密度;δ为桨距角;CT(λ,δ)为转矩系数;V为风轮转速。 进行扭振响应计算前需先计算系统的固有频率,以确定在风电机组运行时是否存在扭振共振点。本文选取某海上5 MW型永磁直驱风电机组为算例,表1为系统的总体技术参数,表2为系统简化后的相关参数。进行海上风电机组的固有特性分析时,一般不考虑系统中阻尼的影响,自由振动的固有频率仅与系统的惯量和刚度有关。基于前述的扭振二质量块模型,在MATLAB中建立海上直驱型风电机组的扭转自由振动方程并求解。表3给出了该风电传动系统的固有特性的计算结果。由于该机组的额定转速为12.1 r/min,由表3计算结果可知,风电机组在运行时不会产生扭振共振,因而需对风载荷下的风电机组传动系统进行瞬态响应分析。 表1 5 MW型机组的总体技术参数 按照表1的机组总体结构参数,基于MATLAB按式(3)~式(16)分别建立风电机组在额定转速下的风剪切效应、塔影效应、湍流效应的风速模型,并根据式(17)进行风轮激励扭矩的计算,可得到不同风速模型在额定风速为11.4 m/s(风轮额定转速为12.1 r/min)产生的气动扭距激励,由图4~图7分别表示。 在进行扭振响应计算时,将上述3种气动载荷及其合成载荷作为系统的激励输入,采用Newmark-β逐步积分法对式(2)进行计算,分别得到了不同风速模型下系统的瞬态响应特性,计算结果以两质量点间的转角差进行表示,见图8~图11。 表2 系统的扭振当量参数 表3 系统的固有频率 图4 风剪切效应下的气动扭矩 图5 塔影效应下的气动扭矩 图8~图11中0~2 s左右范围是由于系统载荷从0突然加到额定载荷后所产生的阶跃负载响应。不考虑加载阶跃负载响应影响,系统运行平稳后,根据扭振转角与扭距之间的换算关系,可得到风剪切、塔影效应和湍流效应下的扭距幅值,经计算后分别为0.43、0.57、9.7 kNm。3种风速模型合成后轴段的扭距幅值为11.9 kNm。 图6 湍流效应下的气动扭矩 图7 风剪切-塔影-湍流效应下的气动扭矩 图8 风剪切效应下两质量点间的转角差 图9 塔影效应下两质量点间的转角差 图10 湍流效应下两质量点间的转角差 结果表明,额定转速下轴段的扭振响应幅值受风剪切和塔影效应的影响较小,受湍流效应的影响较大,3种风速模型合成后的扭振响应相较于湍流效应下的略大。这一结果说明了在系统存在阻尼时,风剪切和塔影效应产生的较小的周期性扭矩波动对系统扭振响应影响较小,而随机性的湍流气动载荷则仍旧会使系统产生扭振。 图11 风剪切-塔影-湍流下两质量点间的转角差 (1)建议采用集总参数双质量模型对海上直驱型风电机组传动系统进行时域瞬态扭振计算与分析,该模型可以更好地评估风电机组传动系统的扭振固有特性。 (2)在模拟实际风速的前提下,获得了由随机风速引起的传动系统输入转矩,并将其作为风电机组传动系统的外部激励引入动力学模型中,使可靠性评估结果更接近工程实际。 (3)实例计算表明,风电机组传动系统的共振点不在机组运行的转速范围内,系统在运行时不会产生共振现象。传动系统的瞬态响应计算结果表明,高速轴在额定转速下受湍流效应的影响较大。建议在进行响应分析时采用3种风速模型的合成力矩作为激励输入。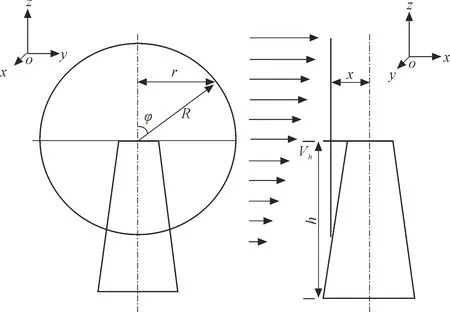
3.4 湍流风速模型
3.5 气动扭转载荷计算
4 扭振瞬态响应计算与分析











5 结论

