伺服阀动压反馈网络流体建模与辨识分析

(1．上海航天控制技术研究所，上海 201109； 2．上海伺服系统工程技术研究中心， 上海 201109)

引言

电液伺服阀是电液伺服系统的核心控制元件，其性能会直接影响整个系统的控制效果[1-6]。在航天领域中对一些大惯量对象的控制，常采用动压反馈伺服阀作为控制元件[7-8]。动压反馈伺服阀的反馈网络可有效地滤掉伺服阀负载压力的振荡，防止因控制不当而造成的大惯量被控系统共振。动压反馈伺服阀中的动压反馈网络决定了其抑制负载压力谐振的能力。

伺服阀动压反馈网络的设计中，需要应用一种流体模型对喷口出油状态进行描述， 并在工作点附近进行线性化处理，从而得到供设计计算使用的线性模型[9]。现有的液压流体设计方法中， 大多将双喷嘴挡板伺服阀的喷嘴挡板段、射流伺服阀导流段等类似条件下的液压流体采用标准流体动力学中的湍流来进行计算，针对现有的基于湍流模型的设计方法[10-12]，按其加工出的动压反馈伺服阀与设计结果差异较大，需要找到一种更为精确的线性模型对反馈网络进行描述，本研究根据理论推导和试验研究，证实了喷嘴出油状态为层流状态，进而对动压反馈伺服阀时间常数的计算方法重新进行了梳理，并通过黑箱辨识方法找到高频段线性模型，利用仿真手段复现了伺服系统负载试验现象。

图1 带动压反馈的伺服系统方块图

1 电液伺服阀动压反馈结构及工作原理

带动压反馈的伺服系统的方块图可以通过图1表示。在电液伺服阀上加入动压反馈，图1中的M(s)环节，即把输出腔压差pL反馈到力矩马达力矩输入端，使力矩马达有一个反作用力矩，该反馈力矩仅在高频下才起作用，所以动压反馈校正相当于引入系统微分校正。

电液伺服阀动压反馈依靠动压反馈组件和反馈喷嘴工作来构成对力矩马达的力反馈控制。动压反馈组件中活塞的两端与伺服阀负载腔pL1，pL2相连，中间的两个反馈腔pC1，pC2分别与左右反馈喷嘴相连，动压反馈活塞的两端布置回位弹簧。动压反馈组件在当负载压差处于稳态时不工作，当负载压差发生突变时，活塞产生运动，反馈腔的压差也随之相应变化，反馈压差经反馈喷嘴射流后作用在挡板上，形成一个与输入信号变化趋势相反的反作用力矩，该反作用力矩阻碍挡板的变化，所以起到增加阻尼作用，电液伺服阀动压反馈的结构组成如图2所示。

2 动压反馈时间常数的试验及物理仿真测定

为了对动压反馈的时间常数τ的模型计算方法进行探究，需要对其进行准确值测定，为后续模型计算结果比对提供依据。为使时间常数的测定值更加准确，采用试验和物理仿真两种方案测定时间常数。

2.1 试验测定

利用伺服阀动压反馈测试系统对伺服阀进行时间常数τ的测定，在测试动压反馈的时间常数时，通过加载阀来对被测试伺服阀的负载腔进行压力加载，给加载阀输入扫频正弦波信号，被测伺服阀不通电，测试系统组成原理如图 3所示。

图2 电液伺服阀动压反馈结构组成

图3 测试系统组成原理图

包含有时间常数τ信息的动压反馈幅值特性曲线测试结果如图4所示。

伺服阀动压反馈试验测试可得到以下结论：

图4 动压反馈幅值特性曲线

试验测试的时间常数τ为0.10，从图4中可以看出，该结果根据前半段曲线进行拟合，但拟合出的结果偏大，该产品实际时间常数约为0.08。

2.2 物理仿真测定

由于曲线拟合方法对实物试验测定结果影响较大，且结果不够精确，故建立了伺服系统物理仿真模型，XX-26A阀的相关参数如表1所示。

表1 XX-26A阀动压反馈主要参数

伺服系统物理仿真模型如图5所示，其中动压反馈参数按表1进行设置。

XX-26A阀的模型如图6所示，在动压反馈模型中设置传感器，可以观测动压反馈效果。

对伺服系统仿真模型输入定点扫频信号，得到的输出结果如图7所示。

为验证仿真系统与实际系统的吻合度，将仿真输出位移信号进行解算，得到系统在该频率点处的幅频和相频特性。用伺服系统的动态测试结果与仿真结果进行比对，如图8所示，实物系统试验如图9所示。

图5 伺服系统物理仿真模型

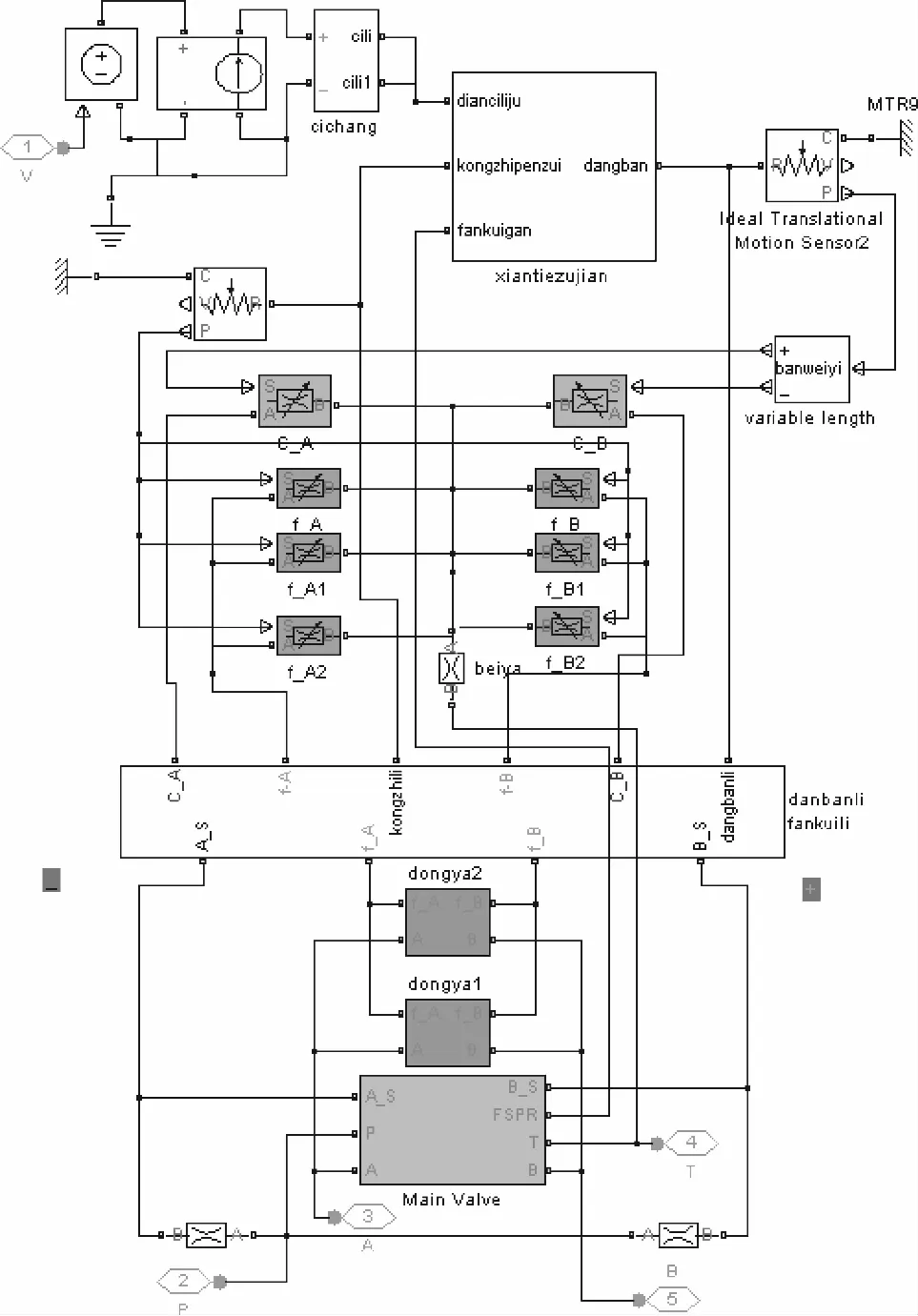
图6 XX-26A阀模型

图7 仿真模型的位置输入和输出信号

图8 仿真与实测结果频域特性对比

图9 系统试验

通过对比可知，仿真系统的频域特性与实测结果较为接近。可以利用仿真系统进行分析。

通过仿真系统的压力传感器可以监测到反馈喷口压力的变化，随着输入信号频率的加大，压力变化如图10所示。

图10 反馈喷口压力变化

从物理仿真结果可得到以下结论：

动压反馈喷口压力变化范围为0.1×10-4～3×10-4MPa，在6.380 Hz前喷口压力变化幅度较小，动压反馈所起作用有限。通过对动压反馈的喷口压力进行解算，得到XX-26A阀动压反馈模块的时间常数τ约为0.083。

3 动压反馈流体模型参数计算方法

为探究动压反馈转折频率与结构参数的关系，利用系统物理仿真模型，对表1中动压反馈模型参数模型进行修改，未加动压反馈模块时，位置伺服系统的频宽约为8 Hz。

3.1 结构参数影响分析

令η=Av/Av1，以负载压力pL为输入，反馈网络的反馈压力pC为输出，当20·lg(pC/pL)为-3 dB时，对应的频率定义为反馈网络的转折频率ωf，即1/τ。定义动压反馈活塞端面直径为dv1、反馈活塞比为η、反馈喷嘴孔径为DN，反馈喷嘴挡板初始间隙为xd0、反馈弹簧刚度为KF且为固定值，即xd0=0.006 m，KF=21075 N·m-1，将参数数值输入仿真系统，由仿真得到的动压反馈转折频率ωf如表2所示。

根据表2中的数据和相关的仿真数据，可以得到如下结论：

(1) 反馈活塞端面积Av1或反馈活塞端面直径dv1对动压反馈转折频率影响较大；

表2 动压反馈转折频率与结构参数的关系

(2) 反馈活塞端面积确定后，适当增大反馈喷嘴孔径DN，动压反馈转折频率将提升，反之，将下降；

(3) 反馈活塞端面积确定后，适当改变反馈比η变化时，转折频率略有变化，变化幅度不大；

(4) 反馈喷嘴与挡板间隙xd0增大，动压反馈转折频率增大，反之，将减小。

明确动压反馈网络结构参数与其动态特性之间的关系后，还要进一步明确动压反馈模块与伺服系统动态特性的关系，这样才能确定何种结构参数的动压反馈模型使伺服系统的性能达到设计要求，具体结果如表3和表4所示。

表3 结构参数与伺服系统频宽关系

根据表3和表4中数据和相关仿真数据，可以得到如下结论：

(1) 一般情况下，动压反馈转折频率不应大幅度超过系统谐振频率。动压反馈转折频率从2.3 ～9.5 Hz左右变化，位置系统均可以得到较高的频宽。但选用转折频率高的动压反馈模块，系统可能得到的最高频宽较选用转折频率低的动压反馈模块低2～3 Hz；

(2) 在动压反馈活塞端面直径dv1和反馈比η为定值且动压反馈转折频率不超过位置系统频宽时，选用大的反馈喷嘴孔径将系统频宽降低，位置超调量减小，使反馈效果明显增加；

(3) 在动压反馈转折频率明显高于位置系统频宽时，动压反馈作用明显降低。

表4 动压反馈结构参数与伺服系统超调量关系

3.2 参数计算方法讨论

根据3.1节对非线性动压反馈对位置伺服系统作用的讨论，为了结构设计方便，需要找到接近的线性化模型，以及时间常数的计算方法。现有求取时间常数τ的算法主要利用湍流模型，但设计结果与试验结果相差较大。这里通过对喷口流体状态的分析，利用层流模型推导出了快速算法和层流算法，并进行了计算结果的比对。

因动压反馈原理为负载腔压差pL变化导致反馈喷嘴腔压差pC变化，通过反馈喷嘴压差将液压力作用于马达上构成力矩负反馈。所以，求解动压反馈力矩M=M(s)分为两步：第一步，求出反馈力矩M与反馈腔压差pC关系，即反馈增益KN；第二步，求pC与pL的关系，用pC=g(s)·pL表示，即求取时间常数τ。

求pC与pL的关系的过程如下：

列出活塞的动平衡方程：

2KF·Xv+(pC1-pC2)Av

(1)

式中,pL1—— 负载腔左腔压力，MPa

pL2—— 负载腔右腔压力，MPa

Av1—— 活塞端面面积，m2

Av—— 活塞的有效面积，m2

mv—— 活塞质量，kg

Bv—— 活塞运动粘性力系数，m2/s

KF—— 单个弹簧刚度，N/m

Xv—— 活塞位移，m

pC1—— 反馈腔左腔压力，MPa

pC2—— 反馈腔右腔压力，MPa

在静态平衡时，方程可简化为：

(pL1-pL2)·Av1=2KF·Xv+(pC1-pC2)Av

(2)

记负载腔压差为pL1-pL2=pL，反馈腔压差为pC1-pC2=pC；则有：

pL·Av1=2KF·Xv+pC·Av

(3)

对上式求导得：

(4)

设反馈腔喷嘴液导为C，则有：

(5)

设Av1=n·Av可得：

(6)

令τ=Av2/2·KF·C，则式(6)可化为一阶环节：

(7)

所以动压反馈力矩传递函数可以表示为：

(8)

动压反馈流量方程为：

Q=C·pC

(9)

动压反馈流量传递函数可以表示为：

(10)

1) 湍流模型算法

反馈喷嘴的液流方式为湍流状态时，经过推导化简，可得：

(11)

(12)

式中，Cq—— 流量系数，const

DN—— 反馈喷嘴孔径,m

xd0—— 反馈喷嘴挡板初始间隙,m

ρ—— 流体介质密度，kg·m-3

pCmax—— 反馈喷嘴最大压差，MPa

计算时取pCmax=pS×10%；

Av=Av1-Av2

式中，Av—— 反馈活塞有效面积，m2

2) 快速算法

RD为动压反馈喷口液阻，则有：

(13)

其中，CD为动压反馈液容，则有：

(14)

动压反馈时间常数τ可按下式计算：

(15)

3) 层流模型算法

反馈喷嘴的液流方式为层流状态时，经过推导化简，可得：

(16)

(17)

4) 计算结果比对

根据快速算法计算，代入参数计算有：

=1.2142×1011

(18)

(19)

时间常数为：

τ=RD×CD=0.0896

(20)

根据湍流模型算法计算，代入参数可得：

(21)

时间常数为：

(22)

根据层流模型算法计算，代入参数得：

(23)

时间常数为：

(24)

三种算法的反馈力矩增益均为：

=3.57×10-9

(25)

试验和仿真结果进行比对，如表5所示。

表5 动压反馈时间常数τ的结果对比

其中快速算法和层流模型算法计算结果最为接近，可以作为设计计算的依据。

4 高频段动压反馈数学模型辨识

伺服系统扫频特性，在10 Hz扫频段内有动压反馈曲线的幅频和相频曲线位于无动压反馈曲线下方，动压反馈起阻尼器的作用，使幅值衰减相位滞后，增大了系统的稳定裕度。在10.40～19.10 Hz内动压反馈起超前校正作用，使系统幅值衰减大幅减弱，且使系统相位提升，扫频测试结果如图11所示。

由于实际动压反馈为高阶系统，而采用的动压反馈模型为一阶超前校正环节，反映在系统上相当于阻尼器的作用，如图12所示，图中实线为未加动压反馈伺服系统频谱，标记线为按照一阶超前校正环节设置的带有动压反馈的系统频谱。

根据冗余伺服系统负载试验结果，冗余伺服系统转折约为10 Hz，由图12可知，动压反馈增大了系统的阻尼系数，但在高于系统转折频率部分，并不具有提升相位的能力，且幅值衰减未有减弱部分，故在该频段内，一阶近似模型与负载试验结果不符。

图11 伺服系统扫频结果

图12 带一阶反馈环节的伺服系统频域特性

根据转折频率后高频段试验现象，考虑动压反馈部分需近似为二阶超前校正模型，利用黑箱辨识方法，将动压反馈数学模型调整为:

(26)

系统频域特性如图13所示，图中实线为未加动压反馈伺服系统频谱，标记线为按照二阶超前校正环节设置的带有动压反馈的系统频谱，在10 Hz后具有提升相位的能力，且幅值衰减程度减弱，与负载试验结果一致，故高频段动压反馈模型应为二阶或二阶以上超前校正环节。

5 结论

针对现有湍流模型计算动压反馈网络的时间常数τ，伺服阀试验结果与设计计算差异较大， 高频段数学模型线性化的建模问题， 本研究提出了一套基于层流流体模型低频段的时间常数τ计算方法，通过黑箱辨识方法找到高频段线性模型，利用仿真手段复现了伺服机构负载试验现象，验证了数学模型的准确性，实现了动压反馈网络的线性化模型的建立，为动压反馈设计找到了模型依据。

图13 带二阶反馈环节的伺服系统频域特性