振动环境下O形圈静密封性能分析
(1.河南建筑职业技术学院设备工程系, 河南郑州 450064; 2.浙江工业大学机械工程学院, 浙江杭州 310032)
引言
O形圈因结构简单、密封性能良好而被广泛应用于各种机械设备密封部件中,如核主泵、水下机器人、发动机、飞机伺服作动器等[1-4]。随着我国密封行业的迅速发展,密封件的运用范围愈发广泛,但同时也面临着高速、高压和强振动等更严苛的工况要求。
目前,关于O形密封圈的研究已有不少。莫丽等[5]对D形圈进行有限元分析,研究不同预压缩率对密封圈的性能影响并进行了改进;ZHANG Y等[6]以往复密封中的O形圈为例,利用ANSYS Workbench建立有限元模型,研究了O形圈的工作应力分布和失效机理;郭志攀等[7]从密封材料选择、密封件加工以及沟槽设计等方面对航空液压密封的设计方法进行了分析;JOHANNESSON H L[8]通过对液压缸密封状态的研究, 分析了O形圈本身及其周围密封间隙的影响, 引入空化条件,提出一种通过计算获得O形圈密封区域压力分布,从而计算出不同密封压力和不同滑动速度下的摩擦力、膜厚及泄漏量的方法。以上研究成果在一定程度上揭示了O形密封圈的密封机理,初步明确了结构参数、工况参数、操作参数等相关参数对密封性能的影响;但是,对于考虑密封圈实际使用工作环境的研究较少[9],而大部分密封部件在使用过程中都会由于恶劣的环境、器械设备自身的制造缺陷、安装偏差等原因造成振动,从而引起密封件运动,由于橡胶的黏弹性可导致移位后接触面恢复中的应变相滞后,使密封面不能迅速追随间隙波动,而在介质压力较高时,主密封面无法始终满足密封要求,从而产生泄漏。因此需要在振动工况下保证密封圈的严密性,了解振动工况下密封圈的密封性能尤为重要。鉴于此,目前国内已有相关学者应用数值分析法针对密封圈实际使用过程中的振动情况进行分析,但普遍以振动的形式作为研究对象,而缺乏对密封件在振动工况下的密封行为变化及各因素的影响进行深入的研究[10-11]。
本研究以O形圈为研究对象,借助ANSYS软件建立二维轴对称几何模型,研究振动工况下的密封行为变化,预判振动易失效部位;并对高压振动工况下振动幅值、介质压力对O形圈的静密封性能的影响进行对比分析,总结高压工况下振动幅值及压力的影响规律,以期为改善O形密封圈的实际使用情况、提高其使用寿命提供理论指导。
1 计算模型及方法
1.1 几何模型
图1所示为高压加挡圈的O形圈几何示意图。由图知,该几何结构由聚四氟乙烯(PTFE)挡圈、橡胶O形圈、缸体和活塞杆4部分组成。其中,O形圈及PTFE挡圈尺寸选自GB/T 3452.1-2005《液压气动用O形橡胶密封圈 尺寸系列及公差》,O形圈为φ15.2×2.62 (mm),PTFE挡圈结构尺寸长、宽为2.9×1.4 (mm);采用矩形沟槽,其尺寸严格按照GB/T 15242.3-94《液压缸活塞和活塞杆动密封装置用同轴密封件安装沟槽尺寸系列和公差》设计。定义活塞杆与O形圈接触的区域为主密封面。
1.2 材料的本构模型
橡胶是一种典型的非线性材料,其变形与所受应力之间的关系表现为高度的非线性。许多学者在大量实验的基础上提出了描述该类材料在不同研究侧重点下适用的本构模型如Neo-Hookean、Mooney-Rivlin、Klosne-Segal等[12]。而针对振动工况下O形圈性能的研究,橡胶材料应力松弛、应变滞后等特性不容忽视,因此为使有限元模拟仿真更接近实际情况,综合采用较为经典的二项参数Mooney-Rivlin超弹模型和Prony剪切响应黏弹模型作为丁腈橡胶材料模型。其中,Mooney-Rivlin 超弹模型中,C10=0.2,C01=6.0,d=0.000279[13];Prony黏弹模型中,加权系数αi和松弛时间τi分别取:α1=0.33333,τ1=0.4,α2=0.33333,τ2=0.2[14]。活塞杆和密封腔体材料均为常用金属材料,由于金属材料的弹性模量远大于橡胶材料的弹性模量,因此进行有限元仿真分析时将金属部件作刚体处理。取密封沟槽与O形圈的摩擦系数为0.25,PTFE挡圈与活塞杆的摩擦系数为0.1[15]。

图1 有限元仿真用几何模型
1.3 有限元模型及边界条件
建立有限元分析模型时,O形圈和PTFE挡圈均选用平面六节点单元 PLANE183。通过网格无关性验证分析发现,当网格数目在65000~120000范围内时能使计算数据误差小于5%,因此本研究在兼顾计算效率和精度的情况下,对有限元模型采用自由网格绘制,特别是活塞杆与O形圈接触对的网格对精度要求较高,因此对接触区域网格局部加密,划分后的有限元模型如图2所示,网格数量为77150个。设置挡圈与活塞杆、挡圈与沟槽、挡圈与橡胶O形圈、橡胶O形圈与沟槽4个接触对,接触方式均为“面-面”接触, 接触类型为刚-柔接触,接触算法采用加强拉格朗日法[16]。

图2 有限元模型
具体的边界条件如下:所有过程中缸体均施加位移全约束。对活塞杆施加径向向右的过盈量位移,直至密封圈达到初始安装预压缩状态;再在加压过程中,对介质侧与流体存在潜在接触可能的密封件表面施加流体压力载荷,模拟流体压力施加过程,其中,流体压力边界精确解的确定采用逐点搜寻实现;再对活塞杆施加径向向左/右方向如图3所示振动幅值L的位移,以模拟活塞杆径向振动情况,从而研究振动环境下各因素对O形圈静密封性能的影响。
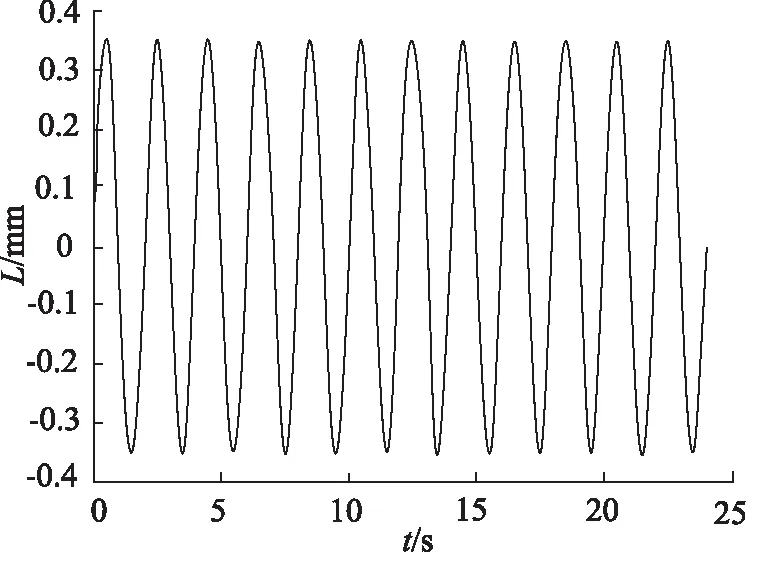
图3 振动曲线
2 计算结果分析
2.1 振动过程中O形圈力学性能
图4a和图4b分别示出了挡圈和O形圈在振动过程中各个时刻的最大Von Mises应力σmax的变化曲线。其中,分析所用密封压缩率为12%,密封介质压力为21 MPa,振动幅值为0.3 mm。-h表示活塞杆远离密封圈振动,0表示活塞杆回到预压缩初始位置,+h表示活塞杆压紧密封圈振动。
由图4a可知,在振动工况下,模拟计算所得挡圈的Von Mises应力随着活塞杆振动呈周期性变化,其中最大Von Mises应力值是预压缩阶段的2倍,突然的应力集中,容易引起挡圈材料的挤压破裂失效。而在活塞杆振动远离阶段出现应力峰值,这是由于活塞杆的振动远离使密封间隙增大,使O形圈被加剧挤入密封间隙,从而挤压挡圈,造成挡圈应力集中,如图5b所示,可以看到挡圈受活塞杆和O形圈双重挤压处应力最大。而4 s活塞杆振动远离回程时的Von Mises应力比6 s活塞杆振动压紧回程时的大,究其原因,是因为振动远离造成的密封间隙增大使O形圈挤入间隙严重,活塞杆回程时挤压O形圈,从而对挡圈造成挤压,因此此时的Von Mises应力值比预压缩状态时大,如图5a所示,可以看到O形圈在密封间隙处严重变形。

图4 振动工况下密封件应力

图5 振动工况下密封件应力
图4b所示的振动工况下的O形圈的Von Mises应力的变化特性正好对应上述挡圈的应力变化。每1振动周期的最大值出现在振动远离回程阶段,且第2周期之后的最大值比第1周期的大,这是由于挡圈材料的回弹性较差,活塞杆振动远离阶段使密封间隙增大,造成O形圈加剧挤入密封间隙,因此振动远离回程阶段活塞杆对O形圈挤压加剧,从而造成此时应力集中严重。而O形圈的最大Von Mises应力值为17.005 MPa,比挡圈的应力值小很多,且在振动压紧阶段挡圈出现严重的应力集中,而此时O形圈应力较小,表明挡圈有效防止了O形圈的损坏,但在实际使用中,应提高挡圈的回弹性,防止振动造成O形圈的挤裂破坏。
图6所示为上述工况下的主密封面各个时刻的最大接触压力pmax变化曲线。由图可以看出,任一时刻都满足密封要求,但活塞杆振动远离阶段会出现接触压力最小值,此时极容易发生泄漏。而在振动压紧阶段主密封面的接触压力出现先减小后急剧增大现象,这是由于密封间隙急剧缩小,造成O形圈被挤出密封间隙造成的接触压力减小,随后活塞杆进一步压紧造成的接触压力急剧增加。因此,活塞杆的振动会造成密封件的应力集中,及引起的过小或过大的接触压力都会使密封件密封作用减弱甚至失效。

图6 主密封面的最大接触压力
2.2 介质压力对振动静密封性能的影响
基于上述研究发现,在活塞杆振动远离阶段出现最小的接触压力,此时极容易出现泄漏,因此对不同介质压力及振动幅值进行详细分析,研究振动对不同工况的影响规律。图7所示为介质压力为10, 15, 21, 25, 30, 35 MPa时,振动幅值0.3 mm,压缩率12%下密封件主密封面的最大接触压力pmax变化曲线图。
由图7看出,随着活塞杆的振动,主密封面的最大接触压力会出现一定波动,但不论介质压力如何变化,在活塞杆振动远离阶段出现的易发生泄漏位置的接触压力最小值始终比工作压力大,因此振动工况下,O形圈的密封性不会因为介质压力的变化而出现失效。

图7 不同介质压力下主密封面的最大接触压力
图8所示为上述工况下挡圈和O形圈的最大Von Mises 应力σmax的变化情况。由图8a可以看出,当介质压力较小时,随着介质压力的变化,活塞杆振动压紧阶段即5 s时挡圈的最大值变化较小,而当介质压力较大时,最大Von Mises应力变化规律基本不变,但振动压紧阶段的最大值出现较大变化,而波动逐渐减小。

图8 不同介质压力下密封件的最大Von Mises应力曲线
由图8b看出,O形圈的最大Von Mises应力随着介质压力的增大波动越来越大,且当介质压力较大时,活塞杆振动回程阶段出现较大的应力集中,而在介质压力小于21 MPa时没有出现这一现象,表明介质压力较小时,O形圈被挤入的较少,而较大的介质压力造成O形圈被挤入张开的密封间隙,因此在活塞杆振动远离回程阶段加剧对挤入的O形圈材料的挤压,造成应力集中。因此在介质压力较大时,振动极容易引起密封圈的应力集中,甚至剪切失效。
2.3 振动幅值对静密封性能的影响
图9所示为压缩率12%,介质压力为21 MPa,振动幅值分别为0.1, 0.2, 0.3, 0.4, 0.5, 0.6 mm时,挡圈和O形圈的最大Von Mises应力σmax变化曲线。
由图9a看出,随着振动幅值的增大,挡圈的最大Von Mises应力也随之增大,因此在实际使用中,应严格防止振动发生。但在活塞杆振动压紧回程阶段,挡圈的最大Von Mises应力随着振动幅值的增大反而变小,从图9b发现,O形圈的最大Von Mises应力在这一阶段呈现同样的特点,究其原因,是由于挡圈和O形圈在被压紧又突然放松后,造成的回弹导致了最大Von Mises应力的较大变化。

图9 不同振动幅值下密封件的最大Von Mises应力曲线
图10所示为上述工况下主密封面的最大接触压力pmax变化曲线。由图可以看出,随着振动幅值的增大,主密封面的最大接触压力在活塞杆振动远离阶段不断减小,最小值不断逼近工作介质压力值,因此当介质压力较大,振动幅值过大时极有可能发生泄漏,因此在实际使用中,应严格防止过大的振动发生。

图10 不同振动幅值下主密封面的最大接触压力变化曲线
3 结论
针对振动工况下密封圈的各应力变化,及对不同介质压力与振动幅值,对密封圈处于振动环境中挡圈与O形圈的静力学特性进行了对比研究,通过分析比较发现:
(1) 在振动工况下,模拟计算所得挡圈的最大Von Mises应力值是预压缩阶段的Von Mises应力的2倍,突然的应力集中,容易引起挡圈材料的挤压破裂失效,且最大Von Mises应力出现在活塞杆振动压紧阶段。而O形圈的最大Von Mises应力在活塞杆振动远离回程阶段出现应力峰值,这是由于挡圈材料的回弹性较差,O形圈被挤入过大的密封间隙造成的。因此在实际使用中,应提高挡圈的回弹性,防止振动造成O形圈的挤裂破坏;
(2) 振动幅值恒定,介质压力改变时,密封圈的密封性不会随着介质压力的变化而发生较大改变。但当介质压力较小时, O形圈被挤入密封间隙的较少,而较大的介质压力造成O形圈被挤入张开的密封间隙,从而使活塞杆挤压O形圈材料,造成应力集中。因此在介质压力较大时,更需要注意防震;
(3) 介质压力恒定,改变振动幅值进行分析发现,随着振动幅值的增大,挡圈的最大Von Mises应力也随之增大,因此在实际使用中,应严格防止振动发生。而随着振动幅值的增大,主密封面的最大接触压力在活塞杆振动远离阶段不断减小,最小值不断逼近工作介质压力值,因此当介质压力较大,振动幅值过大时极有可能发生泄漏,因此在实际使用中,应严格防止过大的振动发生。

