磁流变阻尼器的自适应时滞补偿实时混合试验

王 贞， 王纯鹏， 吴 斌

(1. 哈尔滨工业大学 结构工程灾变与控制教育部重点实验室，哈尔滨 150090; 2. 哈尔滨工业大学 土木工程智能防灾减灾工业和信息化部重点实验室，哈尔滨 150090; 3. 哈尔滨工业大学 土木工程学院, 哈尔滨 150090)

自日本学者Nakashima等[1]提出实时混合试验方法以来，各国学者开展了一系列研究工作，逐步确立了核心问题-时滞及补偿。试验过程中伺服加载系统从接收指令到实现指令所需要的时间，即系统时滞[2]。已有研究表明，作动器加载时滞会为试验带来误差[3]，对于刚度试件引入等效负阻尼而可能导致试验失稳[4]，威胁试件和试验系统的安全。本质上，时滞问题就是系统动力响应滞后问题，完全可以从闭环控制与参数优化的角度降低系统时滞；不过，鉴于加载系统已经得到良好设计与参数优化，这么做很难大幅降低系统相位滞后。目前该领域多采用位移预测方法[5-7]补偿系统时滞，该类方法通常假定时滞为常数，并通过前期离线估计得到；试验过程中预测时滞时长后试验子结构的位移，并提前一个时滞时长发给作动器。该方法不适用于变时滞系统且在位移信号含有较多高频成分的情况中，有时性能较差。实时混合试验除了时滞问题之外，可能的研究方向还包括逐步积分算法、试验应用和试验平台等。

磁流变阻尼器作为智能减振装置，经过多年发展，其应用范围更加广泛[8]。随着磁流变阻尼器控制算法的复杂化[9-11]和尺寸的大型化，数值模拟常不能准确反映其控制性能，需要通过试验进一步检验。文献[12-13]分别使用实时混合试验技术对含有磁流变阻尼器的多层钢框架、隔震支座进行性能研究，评估了磁流变阻尼器的减振效果。由于时滞引起的试验误差会对磁流变阻尼器性能评估产生不利影响，为了更准确地评估磁流变阻尼器的减振效果，因此有必要解决作动器加载中的时滞问题。

磁流变阻尼器是速度相关型装置，具有强非线性[10]，导致加载系统性能时变，表现为试验中时滞波动，进一步增加了实时混合试验时滞补偿的难度。为解决变时滞补偿问题，文献[14-16]提出自适应时滞补偿方法，但是这些方法往往不具有较强的普遍性。文献[17]提出了基于加载系统离散模型参数在线识别的自适应时滞补偿方法，本文在该方法的基础上进一步完成磁流变阻尼器的实时混合试验的数值模拟和真实试验。

1 自适应时滞补偿原理

文献[17]采用自校正控制方法[18]的基本原理，实现了实时混合试验中加载系统时滞的自适应补偿，其原理如图1所示。

图1 自适应时滞补偿实时混合试验的原理

1.1 离散模型

由图1可知，伺服加载系统及试件作为一个整体，使用输入/输出模型可以方便地刻画其外部特性，从而简化控制器设计。为了追踪加载系统特性的变化，由作动器离散传递函数出发，建立作动器指令输入与输出之间的关系[17,20]:

(1)

1.2 参数识别

自校正控制方法需要在线识别系统控制器参数，且参数识别方法是保证良好控制性能[19]的关键。对于时变系统的参数识别，文献[17]针对弹性试件使用了带遗忘因子的递推最小二乘法，虽然计算量较小，但主要存在如下问题：当参数初值估计偏差较大时，试验精度及安全难以保证。

为方便表述，将式(1)改写为矩阵形式，即：

(2)

其中，

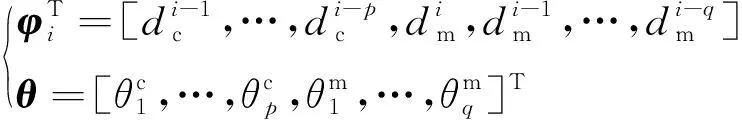
根据矩阵最小二乘法[20]，参数θ的表达式为

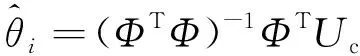
(3)

其中，

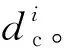
1.3 时滞补偿

在第ti+1时刻，对于式(2)，有：

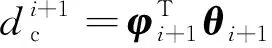
(4)

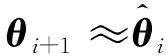
(5)

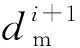
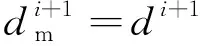
(6)

另外，采用时滞补偿后实测位移与期望位移较为接近，即：

(7)

同时，在式(1)中用期望位移取代实测位移，能提高时滞补偿方法的鲁棒性。鉴于此，实际实施的时候均采用期望位移而非实测位移。

综上，补偿方法为：

(8)

其中

图2 自适应时滞补偿方法流程

1.4 数值模拟

为了检验基于模型参数识别的自适应时滞补偿方法的可行性与补偿效果。选取图3所示的单自由度结构体系进行数值模拟。数值子结构质量取10 000 kg，无阻尼自振周期1 s，阻尼比为5%，由此确定数值子结构刚度为394.784 kN/m，试验子结构为磁流变阻尼器。地震激励为El Centro(NS, 1940)地震波，峰值加速度调整为342 gal。数值子结构采用中心差分法进行求解，积分步长1/1 024 s。由于作动器为位移加载，选取较小的积分步长保证了指令位移更加光滑，从而更好地实现速度和加速度的加载。

图3 结构示意图

根据离线试验数据，使用MATLAB系统识别工具箱拟合得到作动器离散传递函数：

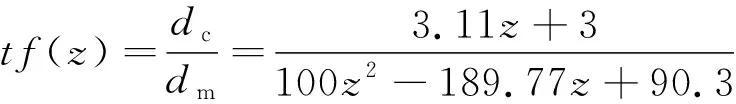
(9)

式中：z为Z变换算子。

对于该作动器模型，理论上应选择4个参数的离散模型[16]进行时滞补偿。数值模拟及试验中均选取三参数离散模型，见式(10)，理由如下：考虑到实际系统中存在未建模动力特性，模型传递函数的阶次可能更高，因此选择的模型参数个数总会低于实际模型传递函数的阶数；较多的模型参数会存在冗余现象，式(3)中矩阵ΦTΦ可能奇异，使得参数估计精度下降，影响试验稳定。

(10)

式(9)表示的线性系统存在位移加载时滞，不能反映加载设备与试件的耦合作用引起的系统动力特性的改变，因此并不能完全反映真实加载过程中的时滞变化。数值模拟中通过改变位移信号的频率可以显著改变系统时滞，为研究方便，取试验子结构的非线性数值模型为

(11)

考虑真实试验中量测噪声及信号A/D及D/A转换噪声，对实测位移dm和指令位移dc分别加入标准差为0.02 mm的白噪声，从而更加真实地模拟实时混合试验。

在加窗最小二乘法中，选取L=300个历史数据点用于参数估计，并设计截止频率为50 Hz的Butterworth滤波器分别对dc和dm滤波，保证参数识别精度。其时滞补偿结果如下，如图4和5所示。

图4 考虑噪声的时不变系统参数估计值

由图4和图5(a)可知，参数估计值整体较为平稳，仅在式(3)中矩阵ΦTΦ可逆性较差时存在较小的抖动，但对时滞补偿效果的影响较小；考虑到完全滤除噪声需要对噪声有先验知识，存在一定困难，因此在第2.3节真实试验中选取了折中的办法。

图5中，使用本文所叙述方法模拟得到作动器指令位移1和实测位移1；使用常规位移预测方法模拟得到作动器指令位移2和实测位移2；参考位移是由全结构数值模拟得到的期望位移。

图5(b)中指令位移与实测位移的相对时间滞后约为16 ms，经时滞补偿后，实测位移与参考位移的相对时间滞后约为1 ms；实测位移2与参考位移幅值误差约为0.2 mm；实测位移1与参考位移幅值差约为0.02 mm，偏差达到噪声的级别。整个模拟过程中，实测位移2与参考位移存在一定偏差，导致试验子结构加载速度与真实情况不同，导致速率相关的阻尼试件的反力也存在偏差，使用常规方法的试验结果不能完全真实地反映原型结构在地震作用下的响应；但实测位移1与参考位移吻合良好，说明本文所阐述的方法相比常规位移预测时滞补偿方法，能够更加真实地再现地震作用。需要说明的是，因为此处的系统模型忽略了磁流变阻尼器与作动器之间的相互作用，系统时滞变化相对较小，所以常规方法总体上也表现出不错的性能。

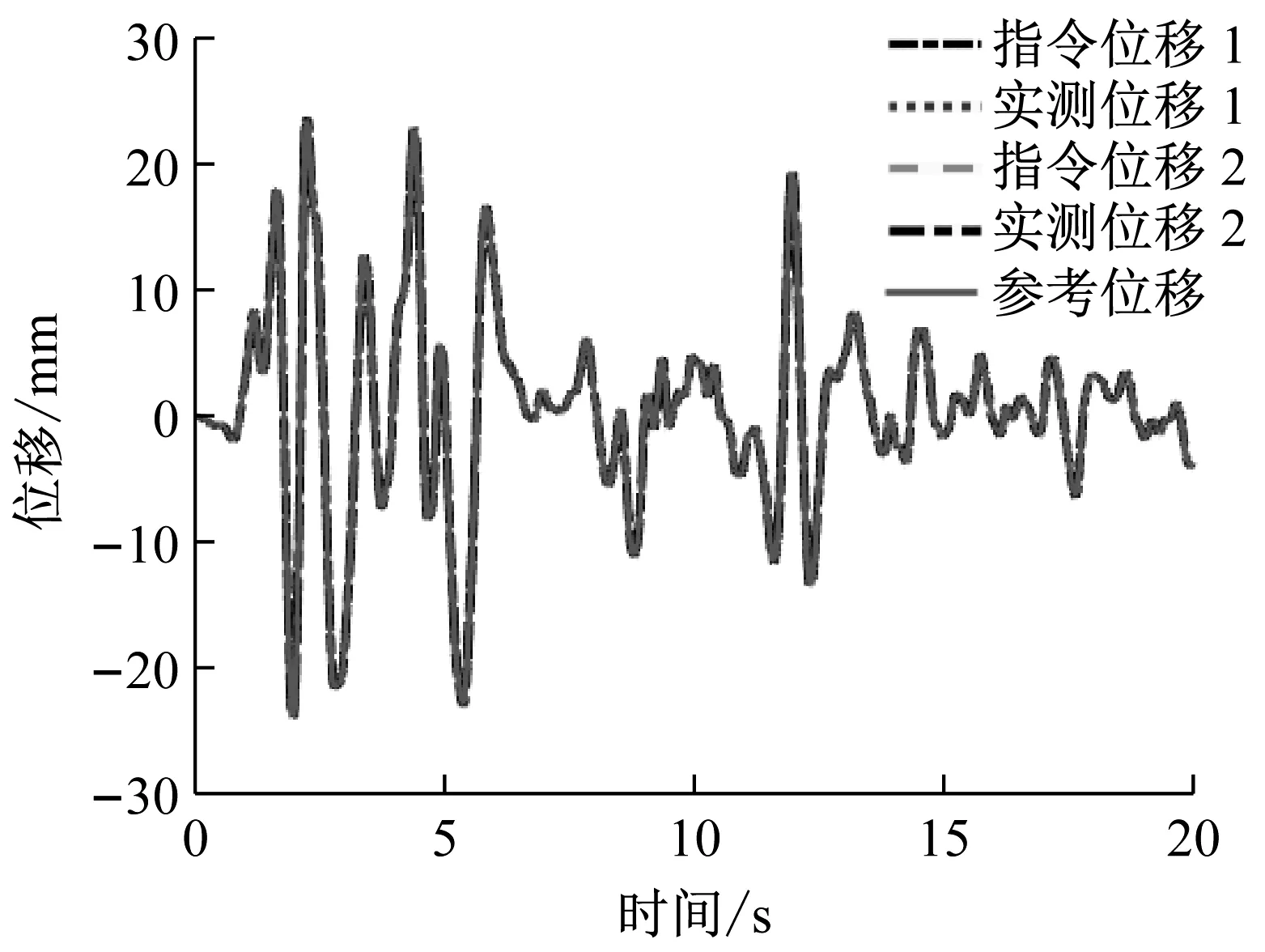
(a) 全局图

(b) 局部图

2 磁流变阻尼器混合试验

2.1 试验模型概况

原型为图3所示的单自由度结构，其中数值子结构参数同第1.4节，地面峰值加速度(PGA)调整至34.2 gal和57.7 gal。试验子结构为美国LORD公司生产的磁流变阻尼器(MRD)，型号RD-8040-1，如图6所示。阻尼器活塞最大行程为5.5 cm，线圈电阻为5 Ω，最大持续输入电流为1 A。在本文试验工况下，阻尼器最大出力约1 kN。

2.2 半主动控制算法

国内外研究人员提出了多种磁流变阻尼器半主动控制算法，主要有Bang-Bang控制、逆模型控制和智能控制等。本文采用线性二次型LQR经典控制计算最优控制力u，结合Bang-Bang-Semi-2控制算法，确定磁流变阻尼器控制电压的法则为

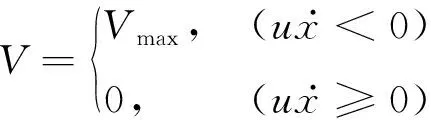
(12)

式中：Vmax为磁流变阻尼器最大控制电压。

该控制算法表明当最优控制力与磁流变阻尼器活塞杆运动方向相反时，施加运动状态阻尼器能实现的最大阻尼力；否则，施加运动状态阻尼器能实现的最小阻尼力。

图6 RD-8040-1磁流变阻尼器

2.3 实时混合试验系统

试验系统由dSPACE板卡、RD-8040-1磁流变阻尼器、伺服加载系统、以及电压恒流源组成。其中dSPACE板卡包含A/D、D/A转换功能、半主动控制功能、求解与运算功能等；电压恒流源将dSPACE输出的电压信号放大输入至磁流变阻尼器，从而快速改变磁流变阻尼器的磁场和阻尼力。

试验主体流程如下：在上位机中使用MATLAB工具箱Simulink编辑计算程序，编译下载至dSPACE板卡，实现与MTS控制器交互通信，从而实现任意位移信号的加载。本试验在哈尔滨工业大学结构与抗震实验中心完成，试验加载系统，如图7所示。

图7 实时混合试验加载系统

前期数值模拟结果以及不同离散模型的初步试验结果表明，三参数系统离散模型能够较好地描述系统动力特性，因此试验中选择三参数模型开展时滞补偿，初步确定控制器为：

(13)

由于逐步积分算法时间步长较小，指令位移增量较小，阻尼器位移响应在一段时间内可能接近线性变化，此时参数估计对噪声更加敏感。若取三步连续的信号进行参数估计，可能会导致参数估计值剧烈抖动，试验稳定性难以保证。采用更大时间范围内的数据，参数估计、时滞补偿会更稳定。为了不增加过多的数据量，每间隔几步选择一个数据点。经调试，使用五步间隔信号进行参数估计，可取得较好的试验结果。

综上，最终确定自适应时滞补偿方法为：

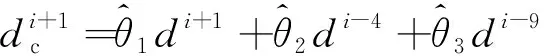
(14)

常规位移预测方法为：

(15)

式中：T为积分步长；δ为作动器时滞；t表示当前时刻；d为期望位移。

2.4 试验结果

本小节对比自适应时滞补偿方法及常规位移预测时滞补偿方法的试验结果。为方便表述将本文使用的自适应时滞补偿方法称之为新方法，将常规位移预测方法称之为常规方法。试验地震动为El Centro波，共4个工况，见表1。

试验过程中，力信号经由MTS控制器传输至dSPACE时A/D转换过程中噪声电平较大，无法获得光滑的力信号，需进行滤波处理。本文采用均值滤波器(即Simulink中Mean Value模块)，即以十个采样步长力信号的平均值作为最终的阻尼力。下面以工况3试验数据为例说明试验结果。

表1 磁流变阻尼器实时混合试验工况表

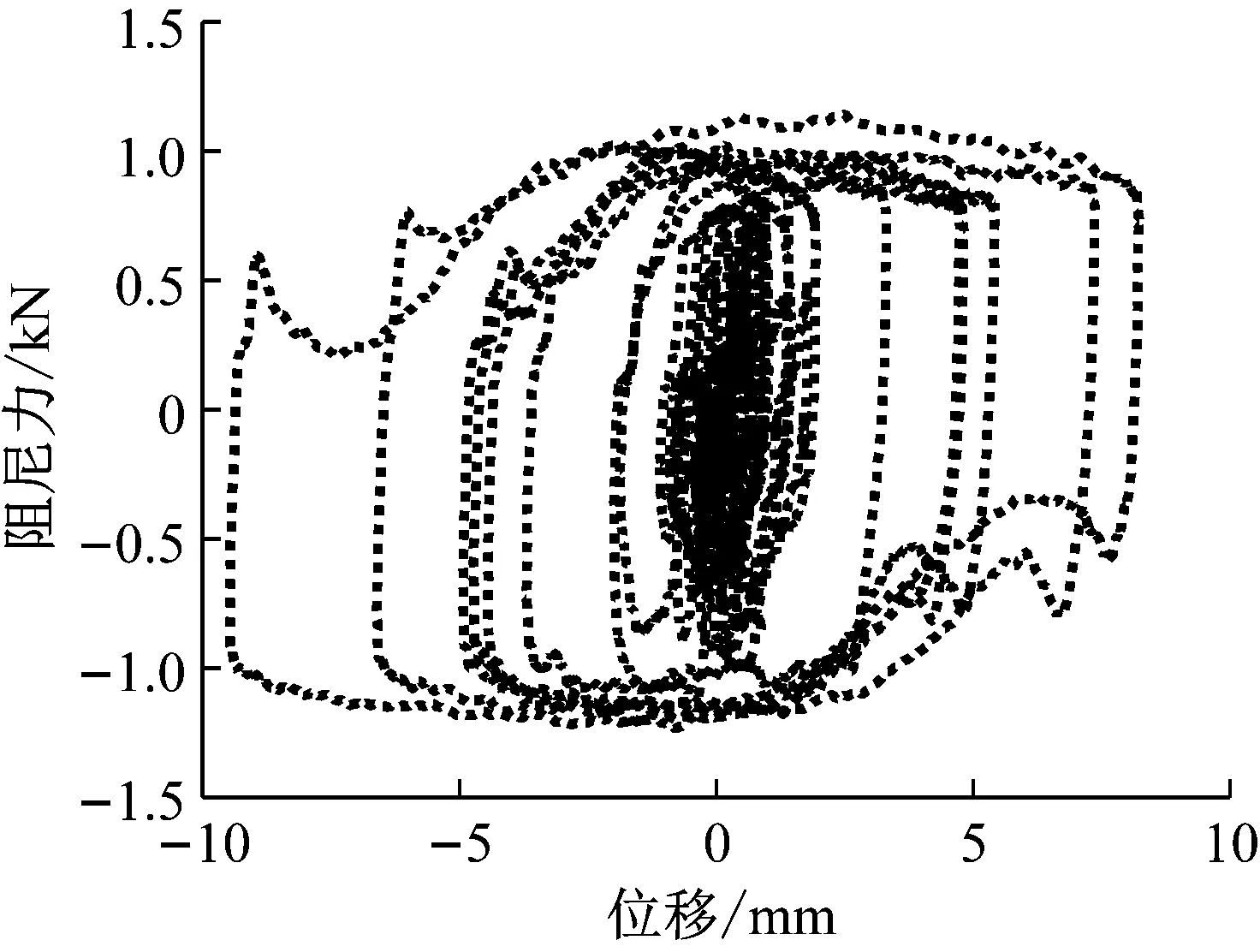
图8 工况3磁流变阻尼器滞回曲线

图8表明，磁流变阻尼器在不同的位移幅值下阻尼力与位移关系呈现较强的非线性。在位移峰值处，作动器缸体腔内油压换向，作动器活塞杆反向运动，此时加载系统的动力特性变化较大；图9表明，自适应参数θ在整个试验中变化较为明显，说明新方法能根据控制目标完成参数的自适应调整，并很好地捕捉系统特性变化，达到自适应时滞补偿的目的。

图9 工况3参数估计值

(a) 全局图

(b) 局部放大图

图10表明，在本文磁流变阻尼器混合试验系统中，系统时滞约为16 ms，作动器指令位移与实测位移关系如图11所示，其“滞回环”的大小反映了时滞的大小。时滞补偿后，实测位移与期望位移相位差对应时间约为1.8 ms，可见新方法具有良好的补偿效果；在图10(b)中位移峰值处，即作动器活塞杆反向运动时，实测位移略小于期望位移，没有出现常规位移预测方法的响应超调现象，试验过程偏于安全。

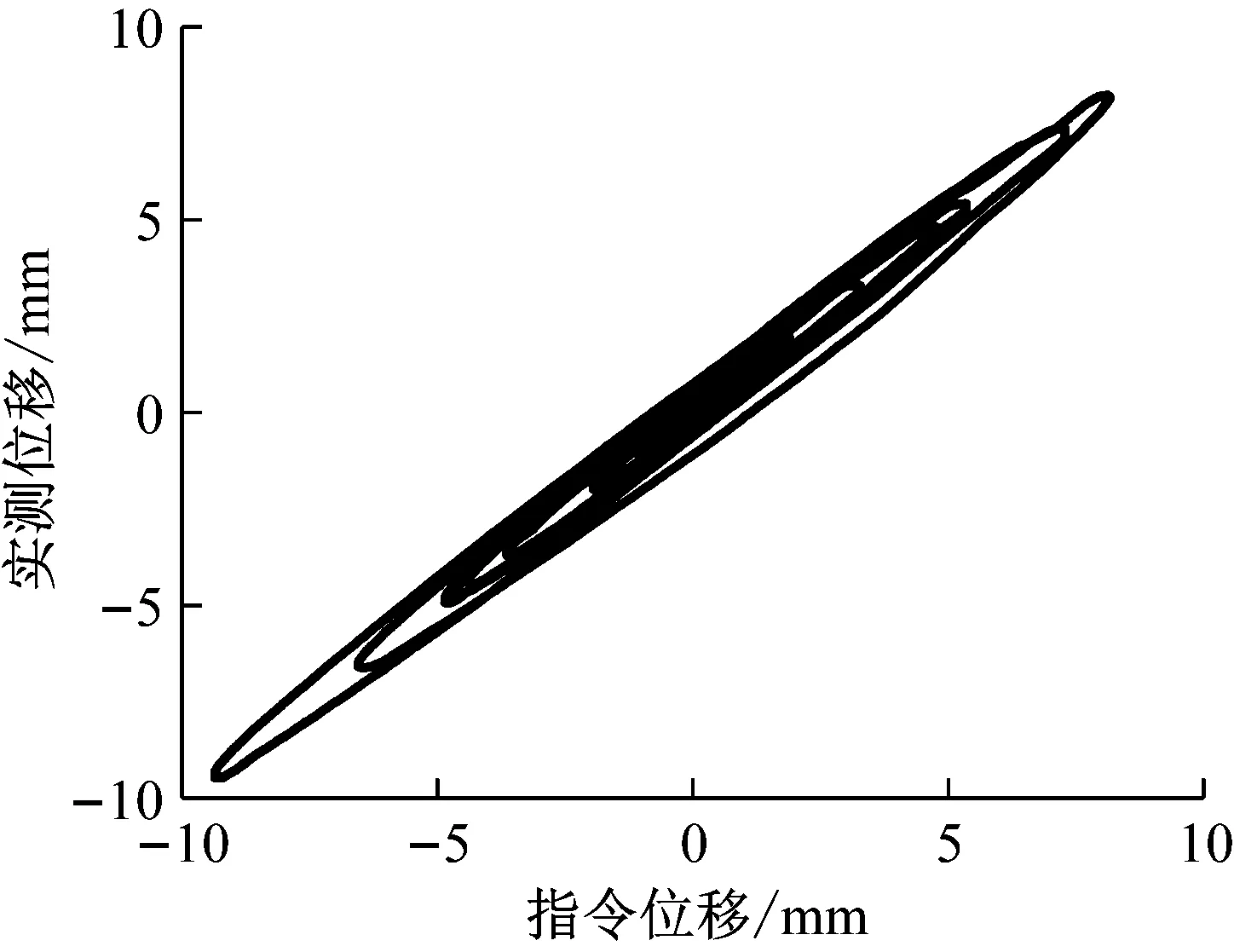
图11 作动器指令位移与实测位移关系

为了评估两种方法性能，定义方均根误差RMSE、误差方差VAR、最大幅值误差MTE三个性能指标，计算公式如下：

(16a)

(16b)

(16c)

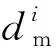
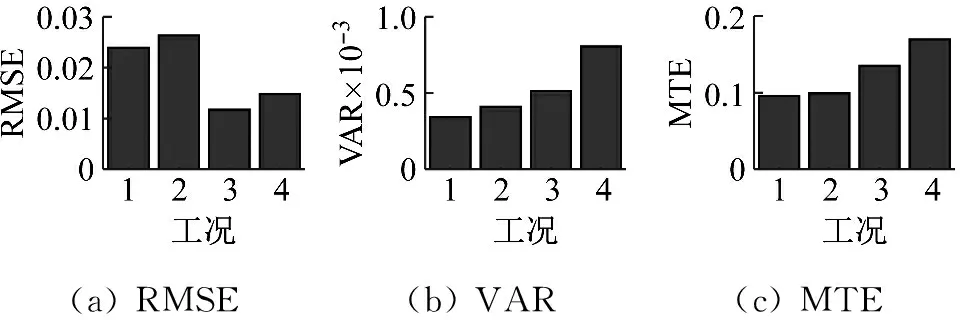
(a) RMSE(b) VAR(c) MTE

图12 性能指标结果图

Fig.12 Results of the performance indicators

由图12可知，在相同PGA条件下，对于指标RMSE与VAR，新方法在时滞补偿、抗噪性能方面优于常规方法，即新方法的实测位移与期望位移更接近。对于较小的地震激励工况，常规方法与新方法的MTE指标接近；对于较大的地震激励，新方法的MTE指标优于常规方法。

对于最大位移幅值较小的工况，作动器负载较小，系统时滞变化不明显，时滞接近于固定值，新方法与常规方法均能很好地补偿系统时滞。对于最大位移幅值较大的工况，系统动力特性变化明显，此时常规时滞补偿方法难以适用，新方法可以很好地追踪系统动力特性变化，可较好地补偿系统时滞，提高试验精度。对于最大位移幅值较大的工况的某些位移相对较小的时间段，参数估计精度容易受到噪声等因素的影响，从而影响时滞补偿效果；此时不进行参数更新能得到较好的补偿效果。

3 结 论

本文采用基于模型参数识别的自适应时滞补偿方法，分别开展了磁流变阻尼器实时混合试验的数值模拟和真实试验，主要结论如下：

(1)基于模型参数识别的自适应时滞补偿方法适用于时变系统，可以实现自适应时滞补偿的目的。

(2)不同试验工况的试验结果表明，试验系统时滞波动不明显时，自适应时滞补偿方法的时滞补偿效果与基于位移预测的补偿方法相近；试验系统时滞波动明显时，自适应时滞补偿方法的时滞补偿效果优于常规补偿方法。