多源时变激励下两级直齿轮传动系统有限元建模方法研究

乔自珍， 周建星,2， 章翔峰

(1. 新疆大学 机械工程学院，乌鲁木齐 830047； 2． 重庆大学 机械传动国家重点实验室，重庆 400044)

齿轮传动系统具有效率高、结构紧凑、传动比稳定等特点，成为机械传动中最重要的形式之一。齿轮传动系统正朝着高速、重载、轻型的方向发展，在实际工作中系统受到内外激励的作用，不可避免的会产生振动与噪声[1]。齿轮系统结构的复杂性，以及各种非线性因素的存在，都给齿轮系统的动力学建模带来困难。

在模型建立方面，齿轮系统动力学模型最初仅有一对简单齿轮副组成，后来逐渐包含齿轮、轴承、传动轴和箱体等[2]。Neriya等[3]较早地将有限单元法引入齿轮转子系统动力学的研究中，建立了包含定值啮合刚度的线性模型；Lee等[4]应用广义有限元建模方法对由电磁振动器施加的一系列半正弦冲击波的转子-轴承系统模型进行实验，研究了转子系统的瞬态响应问题。随着研究的深入，国内外学者考虑传动系统和结构系统的相互作用，建立齿轮系统耦合模型。Özgüven等[5]建立了轴-齿轮-轴承系统的动力学模型来研究齿轮和轴承位置处的响应；Kubur等[6]建立具有N根轴N-1个啮合副的齿轮系统动力学模型，研究了轴承动载荷和轴段长度之间的关系；钱露露等[7]采用有限元建模方法，建立考虑轴、齿轮、转子陀螺效应的单级齿轮传动系统动力学模型，计算得到系统固有特性；常乐浩等[8]借鉴有限单元法，考虑啮合刚度、齿轮误差和箱体柔性等因素的影响，提出了一种适用于齿轮-轴-轴承-箱体系统的耦合动力学建模方法。上述建模方法在一定程度上建立了齿轮-转子系统的耦合动力学模型，研究了其动态特性，但对于多源时变激励下齿轮传动系统的全柔性动力学建模方法研究较少。

本文考虑齿轮、轴承的时变刚度激励以及误差激励，同时计入传动轴的柔性，把轴-轴承-齿轮进行单元划分，将系统等效为离散单元，建立了系统动力学方程， 分析系统的动力学特性，通过实验验证了该建模方法的有效性。

1 模型构建

1.1 传动系统模型构建

一般的齿轮系统包括输入输出系统，齿轮轴系组成的传动系统，轴承底座组成的结构系统。本文以二级定轴直齿轮传动系统为研究对象，来阐述传动系统有限元建模方法。如图1所示，系统中含有第一级主动轮、从动轮，第二级主动轮、从动轮，输入轴、中间轴、输出轴以及轴上起支撑作用的六个深沟球轴承。

图1 二级齿轮传动系统结构模型

系统的详细几何参数，表1、2所示。

表1 二级齿轮传动系统轴参数

1.2 有限元模型构建

齿轮传动系统是一个具有无穷多个自由度的连续弹性体，采用有限单元法将系统简化为离散单元，把非线性问题转化为线性方程组问题。

采用有限元法对二级齿轮传动系统中的轴、轴承、齿轮，分别进行单独建模，如图2所示。其中第一根轴划分成12个单元、第二根轴划分成8个单元、第三根轴划分成9个单元，分别对每个单元节点进行编号形成有限个轴段单元。每根轴上含有两个滚动球轴承，形成轴-轴承耦合单元；第一根轴第7节点和第二根轴第16节点上分别含有第一级主动轮和从动轮，相互啮合形成第一级齿轮啮合单元；第二根轴第20单元和第三根轴第29单元分别含有第二级主动轮和从动轮，相互啮合形成第二级齿轮啮合单元。节点通过耦合作用实现了轴-轴承、轴-齿轮、齿轮-齿轮的物理连接和受力耦合。

表2 二级齿轮传动系统齿轮参数

实际处理时可根据轴的装配要求、几何形状以及实际精度需求，适当增加轴段节点数目，划分更为详细的轴段单元。

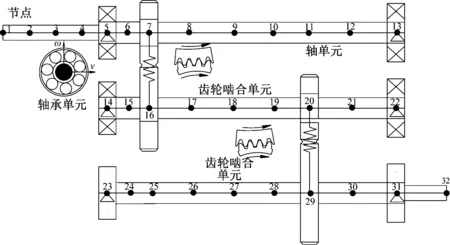
图2 二级齿轮传动系统的有限元模型

2 各单元动力学模型

2.1 轴段单元

轴主要起到支撑回转零件及传递动力的作用，是齿轮传动系统中重要的零件之一。为有效的考虑轴的柔性，建立弹性轴单元模型，如图3所示，可利用空间梁单元理论进行其受力分析。根据表1可知，该齿轮系统模型的轴段宽径比较小，需要考虑剪切变形，因此分析轴段单元采用Timoshenko(铁木辛柯)梁理论。

图3 轴段单元坐标系定义

分析一个梁结构中取出的典型梁单元e，其中梁单元长度为l，弹性模量为E，截面惯性矩为J。单元有2个节点，节点局部编号为i，j。每个节点有2个横向移动自由度和1个扭转自由度，建立如图3所示的轴段单元坐标系，则单元节点位移分量为

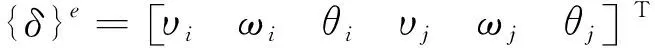
(1)

求得轴单元6×6的刚度矩阵和质量矩阵，由于文章篇幅限制各矩阵的具体形式可参考文献[8]。

结构阻尼在工程中常采用Raleigh(瑞利)阻尼，因此轴单元阻尼为

CS=αMS+βKs

(2)

式中：MS、Ks为轴单元质量矩阵、刚度矩阵。α、β为Raleigh阻尼比例系数，由于传动轴是选用结构钢材料，取α=3，β=0.000 000 8，具体的计算方法可以参考文献[9]。

2.2 啮合单元

建立齿轮系统的动力学模型时，如需考虑齿轮副支撑弹簧的影响，则分析中除了考虑扭转振动外，还必须考虑其他的振动形式。对二级齿轮传动系统进行建模时，首先进行如下假设：考虑齿轮轮齿的弹性和粘性。将其视为黏弹性体，存在扭转振动和垂直轴线方向的平移振动，不存在轴向振动。如图4所示，建立齿轮啮合单元动力学模型。图中p，g分别表示主动轮、从动轮，km(t)表示时变刚度，νp,ωp,θp,νg,ωg,θg分别表示主动轮和从动轮的平移振动位移8及扭转角度，α表示压力角。

图4 齿轮啮合单元动力学模型及时变刚度曲线

各齿轮的广义位移向量可表示为：

{X}={νp,ωp,θp,νg,ωg,θg}T

(3)

齿轮啮合刚度会随着啮合位置的变化而改变，利用有限单元法依次计算出一个啮合周期内若干个啮合位置的啮合刚度，详细计算过程见参考文献[10]。通过线性插值得到其他位置的啮合刚度值，图4为两个啮合周期内齿轮啮合刚度变化曲线。各齿轮沿扭转自由度与平移自由度的振动均会使齿轮副啮合状态发生改变，故齿轮各自由度位移在啮合线方向上的投影矢量为

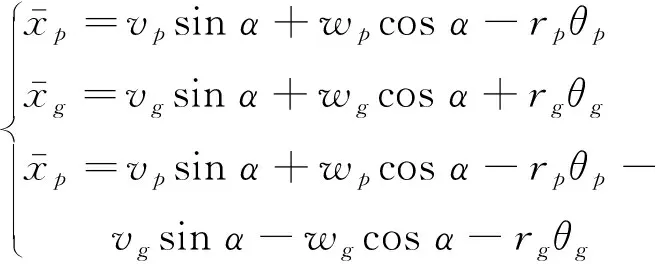
(4)

式中：rp，rg分别为主、从动齿轮的基圆半径。

则齿轮副的弹性啮合力可表示为

Fk=km(t)(υpsinα+ωpcosα-rpθp-

υgsinα-ωpcosα-rgθg+e(t))

(5)

式中：e(t)表示综合误差，其中，e(t)=e1sin(2πfm1t)，e1为误差幅值，fm1为第一级啮合频率。

2.3 轴承单元

轴承主要承担对轴系的支撑作用，连接轴系与箱体组成减速器结构系统。如图5所示：深沟球轴承模型及两种承载形式。

(a) 深沟球轴承动力学模型(b) 奇压(c) 偶压

图5 深沟球轴承动力学模型及两种承载形式

Fig.5 Dynamic model of deep groove ball bearing and two bearing forms

通常，轴承的运动形态分为两种情况：一种是径向载荷落在最下方滚子上(奇压)图中(b)所示；另一种是径向载荷落在最下方两个滚子中间(偶压)图中(c)所示。由文献[11]查阅得到深沟球轴承的基本参数，求出轴承的曲率和与曲率差，表3为轴承基本参数以及计算数值。

轴承的径向位移：

(6)

式中：Qmax为最大法向载荷，D为轴承滚道直径，α为深沟球轴承接触角。

表3 轴承基本参数

奇压时轴承刚度为：

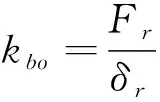
(7)

式中：Fr表示轴承所受径向载荷。

偶压情况下，径向载荷的正下方没有滚子承受载荷，以滚子方位角ψ=±22.5°时的载荷作为滚动体所承受的最大载荷，求出偶压时轴承刚度为kbe。

计算得到，偶压刚度：kbe=8.95×108N/m；

奇压刚度：kb=8.21×108N/m。

则时变刚度：

kb(t)=kbs+kasin (2πfbt+βb)

(8)

式中：kbs为轴承静态刚度，ka为时变刚度波动幅值、fb为轴承通过频率，βb为轴承初始相位角，其中，kbs=(kb0+kbe)/2。

3 系统整体动力学模型分析

3.1 两级相位关系

为建立二级齿轮副模型，确立两级相位关系。首先建立如图7所示的坐标系，假设：vp1所在方向为第一级传动系统主动轮和从动轮的理论中心线方向，ωP1所在方向垂直于两齿轮中心线。

首先做出以下假设：二级定轴齿轮传动系统中，三根轴为空间平行轴系，两对啮合齿轮副始终绕自身轴线扭转振动和在垂直与轴线的平面内平移振动，沿轴线方向不存在振动。如图6所示vp1，ωP1，θp1，vg1，ωg1，θg1为第一级主动轮和从动轮的平移振动位移和扭转角度，vp2，ωP2，θp2，vg2，ωg2，θg2为第二级主动轮和从动轮的平移振动位移和扭转角度。

根据建立的坐标系，齿轮压力角为α，二级齿轮传动系统中三根轴的轴间夹角为β，根据几何关系可知，第二级齿轮啮合线的方向与vp1所在方向的夹角为

α2=β-(π/2-α)

(9)

故在第二级齿轮传动系统中，齿轮各自由度位移在啮合线方向上投影的矢量为

(10)

所以齿轮副的弹性啮合力为

Fk=km(t)·(υp2sinα2+ωp2cosα2-rp2θp2-

υgsinα2-ωpcosα2-rg2θg2+e2(t))

(11)

式中：rp，rg2分别表示第二级传动系统中主动轮和从动轮的基圆半径，km2(t)表示第二级齿轮副时变啮合刚度，e2(t)表示综合误差，其中，e2(t)=e2sin(2πfm2t)，e2为误差幅值，fm2为第二级啮合频率。

图6 二级齿轮传动系统两级相位关系

3.2 单元组装

对全部单元完成分析后，进行单元组装。把各单元的刚度阵，质量阵，载荷向量等物理量，按照有限元的方法进行组装；即按各单元节点编号的顺序，将每个单元刚度矩阵送入总刚度矩阵[K]中对应的行列位置，含有同一编号的不同耦合单元对应该节点的刚度矩阵子块要互相叠加，以建立节点外载荷与位移之间的关系。系统整体自由度的广义位移向量{x}={x1x,x1y,x1θ,x2x,x2y,x2θ,…,xnx,xny,xnθ}，(其中n表示节点数目，n=1，2,…,95)。对于含有三根轴，六个轴承，两对啮合齿轮副的二级齿轮传动系统，考虑边界条件(第一个节点和输入端连接约束了扭转自由度，最后一个节点和输出端连接，承受负载扭矩)采用有限元法，将其划分为29个单元，95个自由度。该二级齿轮传动系统的整体刚度矩阵装配示意图，如图7所示。系统整体的动力学方程可写成：

[k(t)]{x(t)}={F(t)}

(12)

式中：{x(t)}表示节点位移向量；[m]、[c]、[k(t)]分别表示系统整体质量、Raleigh阻尼、刚度矩阵；{F(t)}表示系统所受外部激励。

最后进行动力学计算，由于刚度阵[k(t)]、位移向量{x(t)}都是时间的周期函数，需要借助数值积分进行求解。由于Newmark积分法具备无条件稳定性，计算效率优越于传统的数值方法，故本文在求解动力学模型时采用时域Newmark积分法。

图7 整体系统刚度示意图

4 仿真分析

4.1 传动轴静变形分析

齿轮传动系统在承载作用下，各传动轴均要承受齿轮圆周力和径向力产生的弯矩和扭矩，因而不可避免的会产生各种变形。在不考虑轴单元所受惯性力和阻尼力的影响下，齿轮轴的受力情况可按静力学问题进行分析。通过承载大小与传动轴整体刚度矩阵定义轴变形量。设其变形量为[δS]则

(13)

式中：[ks]表示系统整体刚度矩阵，F表示轴所受载荷。

仿真计算负载扭矩为10 N·m、输入转速500 r/min时，齿轮轴的变形量，如图8所示，(和实际结果相比，图中放大了105倍)。轴上含有轴承支撑以及啮合齿轮副，轴承起约束作用，齿轮副传递载荷。因此，第一根轴在齿轮耦合节点7位置(啮合单元位置)承载最大，具有最大变形量为0.55 μm；第二级齿轮转速小、受载大，因此相比第一级传动轴，第二级传动轴在齿轮耦合处具有更大的变形。第二根传动轴在节点20位置具有最大变形量为1.98 μm；第三根传动轴在节点29位置具有最大变形量为1.70 μm。

图8 轴变形前后示意图

4.2 固有特性分析

当系统外部激励 {F(t)}=0 时，由式(12)可得自由振动方程为

(14)

在模态分析中，阻尼对齿轮系统固有频率和振型的影响不大，故忽略阻尼的作用。

则无阻尼情况下，系统的振动方程为

(15)

将系统固有特性转化为求解系统特征值问题,即

(16)

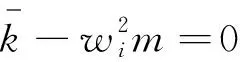
(17)

将计算得到的啮合刚度均值输入两级定轴直齿轮系统动力学模型中，求解得到考虑柔性轴情况下系统的固有频率和振型，系统共计95阶固有频率，前10阶固有频率，如表4所示。

表4 系统前10阶固有频率

本文将连续系统离散为轴-轴、轴-齿轮等基础单元，考虑传动轴几何尺寸、柔性的影响，建立两级齿轮传动系统模型。仿真得到二级齿轮传动系统的振动模式主要包括齿轮副的扭转振动以及传动轴的弯曲、偏摆振动，与文献[2]齿轮系统的固有特性分析结论一致，低阶典型的振动形式如图9所示。第1阶的主要振型是第一级齿轮副的扭转振动，第一级主动轮和第二级从动轮沿顺时针方向扭转振动，第一级从动轮和第二级主动轮沿逆时针方向扭转振动，如图9(a)所示；第3阶的主要振型是第二级齿轮副的扭转振动，和第一阶扭转振动具有不同的振动方向，如图9(c)所示；第6、9阶的主要振型是二级平行传动轴弯曲、偏摆振动，如图9(b)、(d)所示，其中第6阶振型中，轴一和轴三呈现下凹形振动模式，轴二呈现上凸形振动模式；第9阶的三根轴都呈现上凸的振动模式。由于篇幅限制，本文只给出了低阶典型的振动模式，该系统中还具有高阶扭转、弯曲、偏摆振动形式。

传统的集中质量模型，将传动轴简化为扭转变形和弯曲变形的弹性元件，在分析系统的振动形式时，只能分析齿轮副的扭转振动及横向振动，却无法体现传动轴复杂的模态变化。

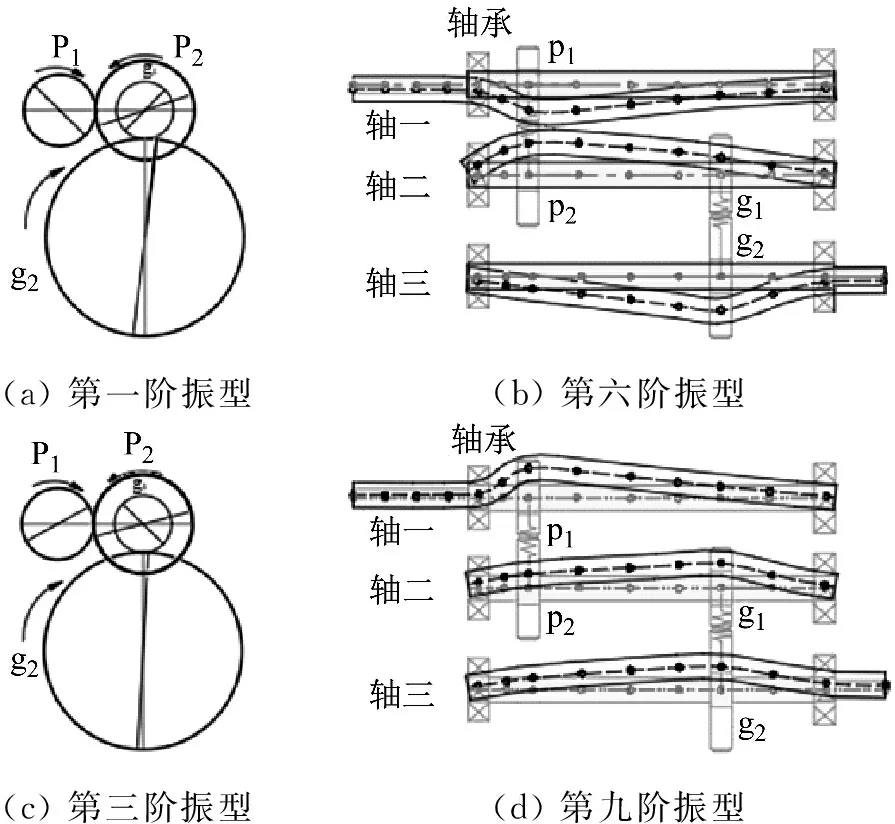
(a) 第一阶振型(b) 第六阶振型(c) 第三阶振型(d) 第九阶振型

图9 齿轮传动系统振型图

Fig.9 Model shape of gear transmission system

4.3 动态特性分析

利用Newmark时域积分方法求解模型，分别仿真得到刚性轴和柔性轴情况下第一级齿轮动态啮合力，如图10所示。

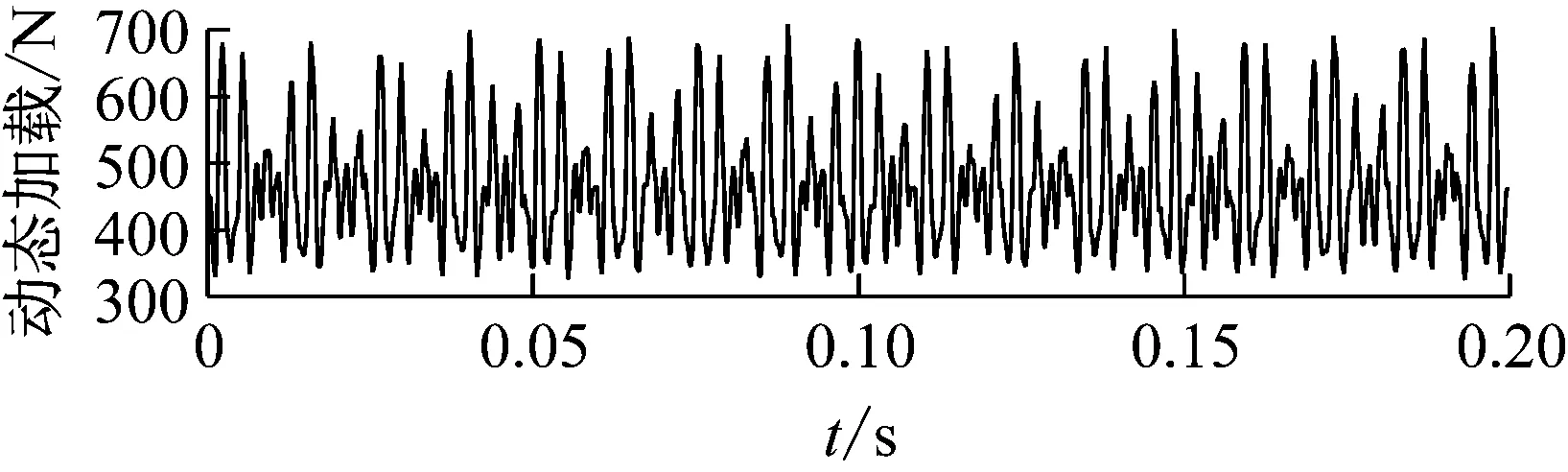
(a) 刚性轴情况下第一级齿轮传动系统载动荷时域历程

(b) 刚性轴情况下第一级齿轮传动系统动载荷频谱图

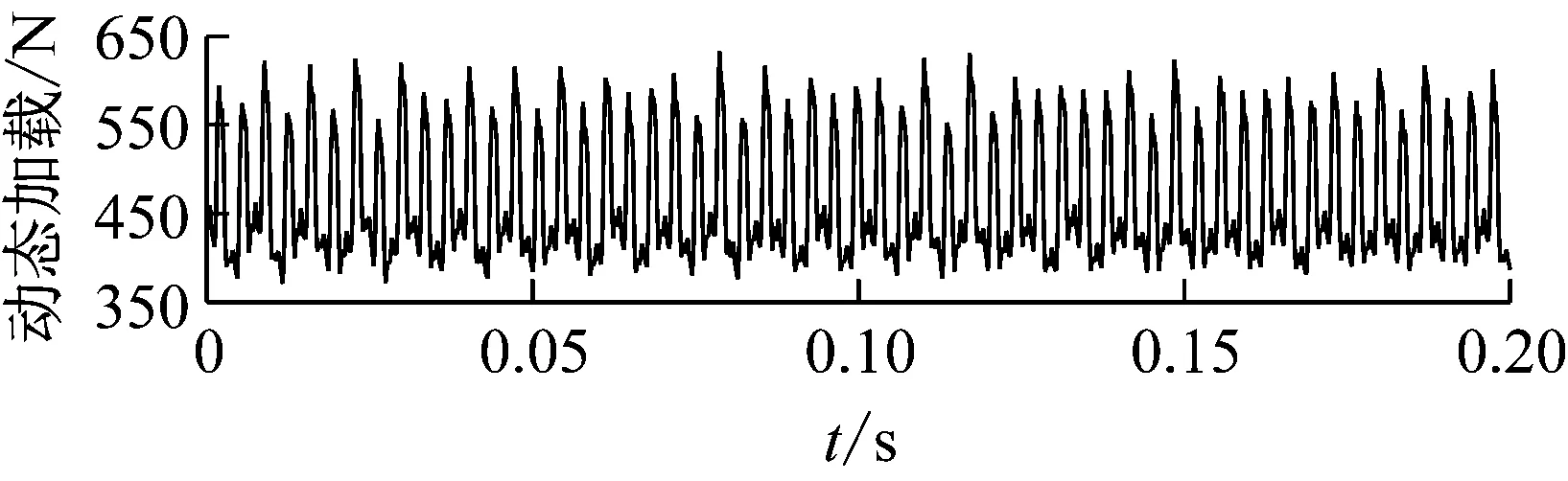
(c) 柔性轴情况下第一级齿轮传动系统载动荷时域历程

(d) 柔性轴情况下第一级齿轮传动系统动载荷频谱图

对比时域历程可以看出，当考虑轴的柔性时，最大动载荷减小，两级齿轮动载荷拍振现象明显减弱，振动信号更加平稳[12]。从频谱分析中可以得到，当把传动轴假设为刚体进行分析时，产生第一阶固有频率(fn1)成分、第一级啮合频率(fm1)及第一级啮合频率的二至四倍频成分、第二级啮合频率(fm2)的二倍频、四倍频、五倍频、七倍频成分，其中第一级啮合频率位置振动幅值最大；当考虑轴的柔性时，动载荷幅值减小，振动响应频率成分减少，这是由于轴的柔性起到隔振作用，减弱了齿轮系统振动的传递。

5 实验验证

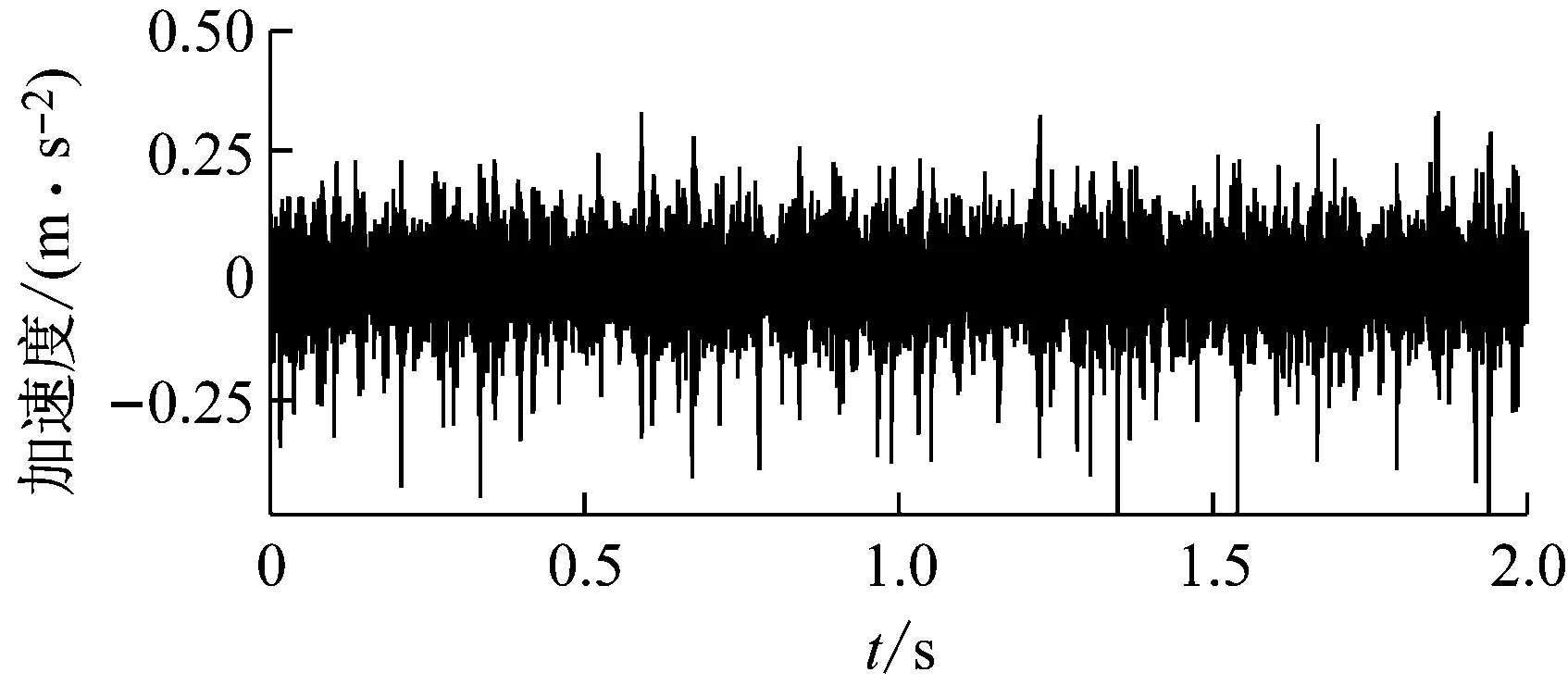
本实验采用的是由SQI公司生产的齿轮传动系统试验台，分析齿轮箱传动系统的动力学特性，采集轴承端盖位置径向加速度的时域信号，如图11(a)所示，其中二级齿轮传动系统与所建模型参数一致。通过将加速度传感器608A11在箱体处进行布点，测点位置如图11(b)所示，使用采集卡DT9837将测得的振动信号进行导出分析。

(a) 传动试验台(b) 测点位置

图11 齿轮传动实验台

Fig.11 Transmission test bench

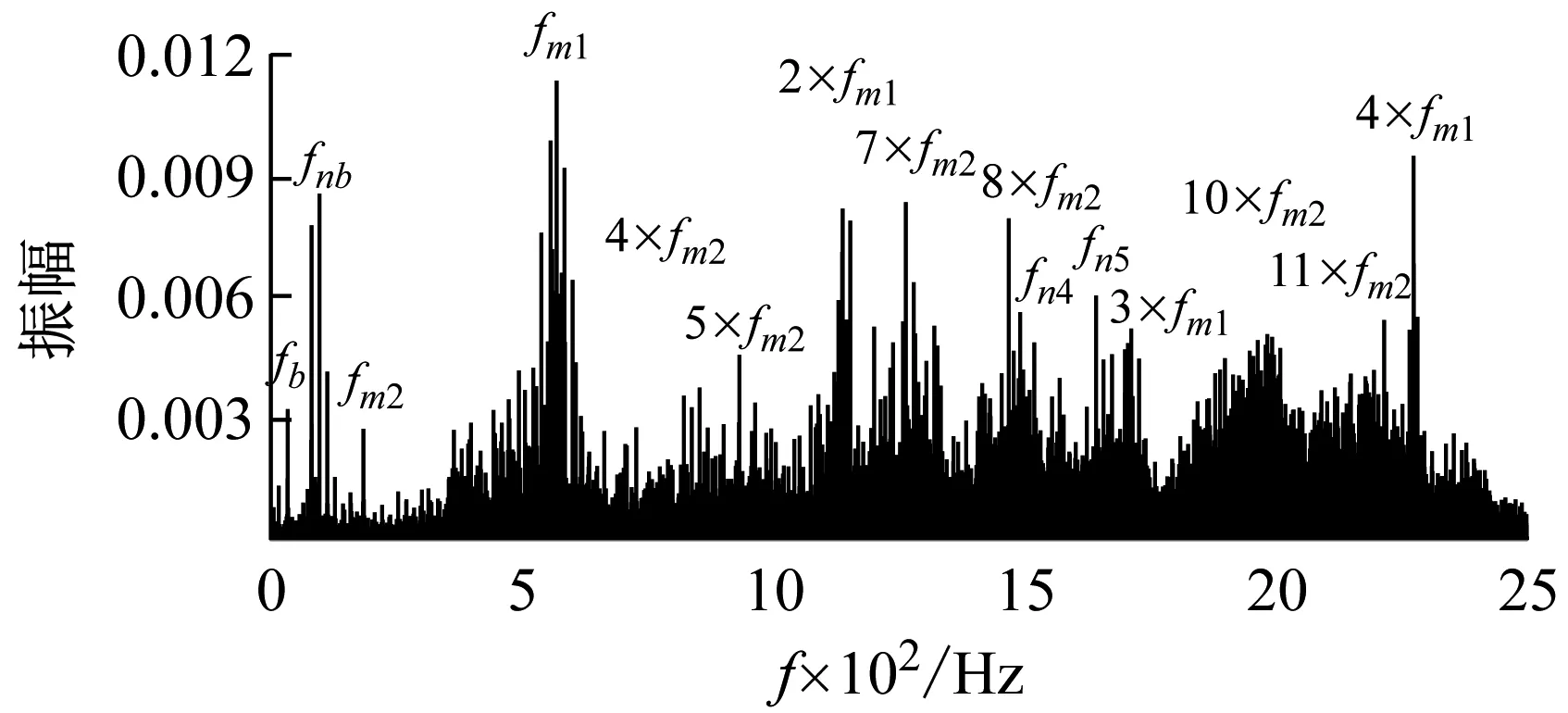
在输入转速960 r/min，负载扭矩10 N·m，采样频率10 kHz的工况下进行实验操作，采集轴承端盖位置径向加速度的时域信号。计算时取若干连续周期，以消除瞬态激励的影响，进行傅里叶(FFT)转换得到频谱图[13]，如图12所示。

从图中可以看出：振动响应中，主要的频率成分为第一级齿轮副和第二级齿轮副的啮合频率(fm1、fm2)及其倍频成分，低频处存在轴承通过频率(fb)成分。

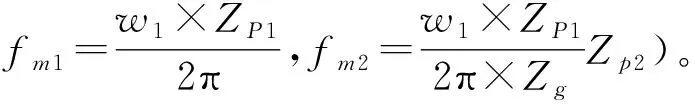
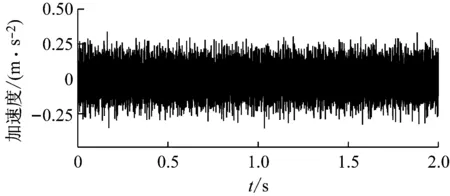
仿真分析二级齿轮传动系统时域信号和频域信号。

如图13所示，除在极少时刻存在少量的振动冲击，振动响应信号相对平稳，节点位移加速度呈现周期性变化。振动响应中，主要频率成分包括：由于模型中计入了轴承刚度的时变性，在低频处产生了轴承通过频率(fb)成分；第一级啮合频率(fm1)及第一级啮合频率的二至四倍频，其中二倍频(1 152 Hz)位置振动幅值较大，这是由于第一级啮合频率的二倍频与系统第5阶固有频率基本一致，使系统振动能量增大；第二级啮合频率(fm2)及其倍频位置也出现振动峰值，其中七倍啮合频率(1 299 Hz)与系统第6阶固有频率基本一致，故在此位置振动最为强烈，系统低阶固有频率如表4所示。第一级啮合频率及二倍频附近，存在明显的由轴承通过频率及其倍频所构成的边频调制成分，仿真与实验结果基本一致。

(a) 加速度时域历程

(b) 加速度频谱图

(a) 加速度时域历程

(b) 加速度频谱图

实验中fnb位置也出现振动峰值，如图13所示，在仿真结果中却没有出现，这是由于仿真计算模型未有效计入实验台基础的动态特性。在实验中，齿轮系统是放置在基础平台上，通过锤击实验测试该基础平台的固有频率即为fnb。

仿真计算与实验测试加速度随转速的变化历程对比，如图14所示。从图中可以看出，当转速从500 r/min变化到3 000 r/min时，仿真计算的加速度随转速变化趋势与实验结果一致。两条曲线均含A、B、二个峰值点，其中A点峰值对应转速为1 700 r/min，传动系统第一级2倍啮合频率与第3阶固有频率(1 055 Hz)较为接近，系统振动加剧；B点峰值对应转速为2 200 r/min，第一级传动系统的啮合频率及二倍频与系统第6、8阶固有频率(1 230/2 875 Hz)相近，第二级传动系统的三倍频(1 270 Hz)与系统第6阶固有频率(1 230 Hz)基本一致，系统发生共振，加速度幅值急剧增加；通过共振区后，加速度随转速变化相对平稳，仿真计算的加速度值与实验测试加速度值相差不大，两条曲线基本吻合。

本模型中采用的是Raleigh(瑞利)阻尼，而当转速不同时系统的振动形式是不一样的，存在不同模态形式，为了克服这一影响，在后续研究中可采取模态阻尼；同时，空气和润滑油产生的耦合作用对系统加速度也会产生影响，造成仿真与实验测试的误差[14]。

图14 不同转速下的加速度仿真与实验对比

6 结 论

本文采用有限元法建立了二级定轴齿轮传动系统动力学模型，考虑轴的柔性，引入两级齿轮相位关系分析了多源时变刚度下系统整体的动力学特性，得到如下结论：

(1)当考虑传动轴的柔性时，动载荷幅值有所减小，振动响应频率成分也随之减少。

(2)有效计入传动轴的柔性，以及轴承刚度与齿轮啮合刚度的时变性，仿真与实验测频率成分分布基本一致。

(3)通过实验测试与仿真计算的对比分析，验证了有限元建立齿轮传动模型的有效性。