GMA的温度特性分析及热形变被动补偿方法研究

刘慧芳， 马 凯， 梁 全， 谷艳玲， 王汉玉

(1. 沈阳工业大学 机械工程学院，沈阳 110870； 2. 香港城市大学 建筑学及土木工程系，香港)

超磁致伸缩材料(Giant Magnetostrictive Material，GMM)是一种在磁场作用下可产生磁致伸缩变形的功能材料，利用该特性可制成输出位移精度达亚微米级的智能构件，即超磁致伸缩致动器(Giant Magnetostrictive Actuator，GMA)[1-2]。GMA的出现为精密与超精密加工提供了新的精密驱动解决方案，可应用于超精密机床、精密仪器、精确定位和主动振动控制等领域[3-6]。

例如，利用GMM产生的微位移可实现高分辨率微进给、小尺寸非圆车削、深孔与异型孔加工等。Guo等[7]研制一种微型镀镍非球面模具的磁致伸缩抛光系统。Wu等[8]提出一种活塞异型销孔加工方法；Liu等[9]研究一种激光烧结振镜的磁致伸缩双级精密驱动系统；徐彭有等[10]研制了利用GMA实现天文望远镜子镜面驱动的精密系统。另外，因其具有机电双向换能特性，GMM亦可用于多功能器件的开发。贾振元等[11]利用磁致伸缩正逆耦合效应开发出集驱动、力测量、输出力感知和输出力可控等功能于一体的力传感执行器。

然而，GMA工作时，存在着线圈焦耳热损耗、GMM磁滞损耗[12]和涡流损耗[13]等生热现象，产生的热量将导致GMA工作温度升高。温升不仅使GMM产生热变形，且引起磁致伸缩系数不稳定[14]，从而严重影响GMA的输出性能。因此，必须采取适当的热形变补偿与抑制方法，以降低在精密与超精密驱动过程中温升对GMA工作精度的影响。

目前，多数利用冷却系统控制温度抑制热变形，或者通过软件算法对热形变数学补偿。这需要在GMA中放置温度控制系统，增加了结构复杂性。而且，智能构件本体对象的时间常数和容量滞后较大，难以实现闭环温度的主动控制。针对此问题，本文首先对GMA的温度变化特性进行深入分析，建立考虑温度影响的GMM多场耦合应变模型，提出一种热形变被动补偿机构，在此基础上对具有热形变自补偿功能的GMA展开设计。最后通过试验分析热形变自补偿过程工作特性。

1 考虑温度影响的GMM多场耦合应变模型

作为驱动元件工作时，GMM的形变主要由磁场和预应力产生，但温度场对应变也有影响，且三个物理场之间存在耦合。为了准确描述GMM的形变、实现对热形变精确补偿控制，建立了考虑温度影响的应变模型。

在GMA系统中，将GMM视为底端具有固定约束、顶端自由无约束且无任何能量损失的圆柱棒体，其长度为l，相对于固定端的纵坐标定义为x，时间用t表示。GMM的总形变由磁场、应力和温度分别单独对材料作用所产生的应变，以及由磁场与热场和应力场的耦合作用产生的应变组成。

仅在应力σ(x,t)单独作用下，GMM应变与磁场和温度无关，用εσ(x,t)表示[15]。当σ(x,t)/σs≥0时，

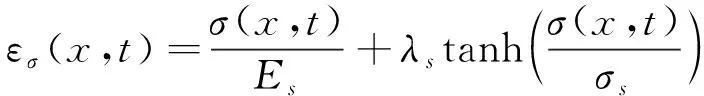
(1)

当σ(x,t)/σs<0时，

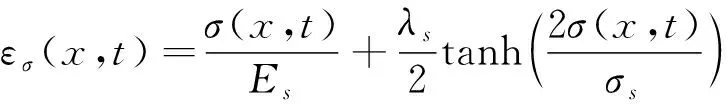
(2)

由式(1),(2)可知，应力产生的弹性应变是非线性的，其可分解为线性和非线性两部分。其中，与磁畴运动无关的部分被视为线性弹性应变，依赖于磁畴运动的部分被视为非线性弹性应变。λs为σ(x,t)=0及T(x,t)=Tr时的饱磁致伸缩系数，Tr表示为初始温度，σs为饱和应力：

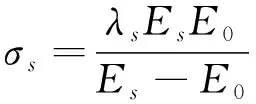
(3)

式中：E0是材料初始杨氏模量，Es是饱和杨氏模量。

GMM在磁场单独作用下产生的应变是源于材料所发生的磁致伸缩过程，该类应变可以用磁化强度表示：

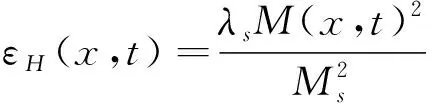
(4)

式中：MS表示GMM的饱和磁化强度。应力和磁场耦合作用使GMM产生的应变用εHσ(x,t)表示，当σ(x,t)/σs≥0时，

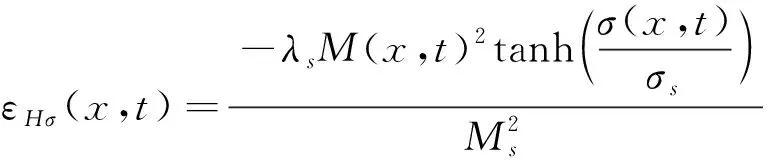
(5)

当σ(x,t)/σs<0时，

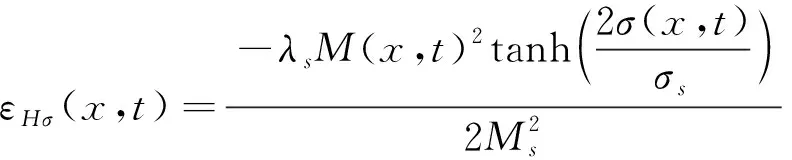
(6)

由式(5)，(6)可以看出，磁场与应力场的耦合效应使材料产生了非线性应变。在GMM被磁化以前，该类应变为零；当磁化强度接近饱和时，应变达到最大值。在无机械约束状态下，与饱和磁化强度对应的应变最大。

当GMM工作在温度为T(x,t)、无应力、无磁场状态，应变完全是热膨胀引起的线性形变。根据热力学定律可知温度升高产生的热膨胀应变为

εE(x,t)=α[T(x,t)-Tr]

(7)

式中：α为热膨胀常数。

热场与磁场耦合作用产生的热磁耦合应变为：

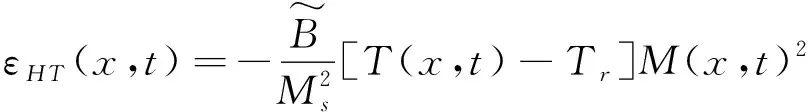
(8)

将上述四部分应变叠加，得到在应力、磁场和温度共同作用下GMM的纵向总应变，当σ(x,t)/σs≥0时，

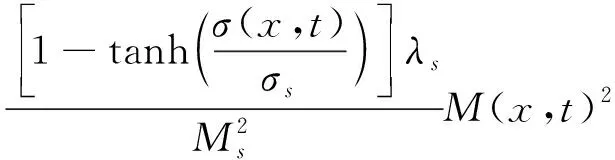
(9)

当σ(x,t)/σs<0时，

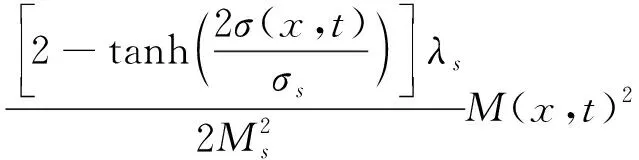
(10)

式(9)～(10)即为考虑温度影响的GMM多场耦合应变模型，其可描述轴向任意点处的应变。该模型不仅考虑了磁化强度和应力对磁致伸缩效应的主导作用，而且包括了温度导致的热膨胀作用，以及温度、应力和磁化强度的耦合效应对磁致伸缩效应的影响。GMM的纵向应变包含线性和非线性应变两部分，其中非线性应变主要由应力、温度与磁场间的耦合作用产生。

温度变化使GMM产生的热变形包括两部分：热膨胀线性应变和热磁场耦合非线性应变。

εT=εE(x,t)+εHT(x,t)=

(11)

从GMM多场耦合应变模型可知，除应力和磁场外，温度也是影响GMM形变的关键。在应用过程中，温度对材料的输出特性有很大影响。本文基于所建立的应变模型，对GMA的温度特性进行分析，以及设计一种具有热形变补偿功能的GMA来抵消温度对GMA输出位移的影响，通过对模型验证来说明模型的有效性。关于温度及热形变问题的具体分析，下文会针对这一问题展开分析和实验。

2 GMA的温度特性分析

输入到GMA中的能量，除部分转化为机械能输出外，很大一部分能量以热量形式耗散，由于内部空间封闭、散热能力差，因此积聚的热量导致系统产生较大温升。温升不仅使GMM产生热变形，而且引起磁致伸缩系数不稳定，进而严重影响GMA的输出性能。因此，本节对GMA内部温度分布规律及变化特性进行分析，研究发热源、温度变化与频率等变量间的关系，进而为GMA的温度控制及热形变抑制补偿提供理论基础。

GMM的磁化过程具有较强的非线性，且温度场与电磁场间存在复杂的耦合关系，所以选择采用COMSOL多物理场耦合有限元法对温度特性分析。其中，通电线圈的电磁效应、GMM的磁化过程由磁场模块分析计算，磁致伸缩过程是通过将磁场模块与机械结构模块耦合进行分析，两模块间由磁化状态变量衔接。采用二维轴对称法建立GMA几何模型，并采用自定义与自适应相结合的方法对模型进行有限元网格划分。利用映射网格方式对GMM、线圈、磁回路等关键部件划分，并根据构件尺寸分别定义网格密度；其它构件利用自适应三角法划分。

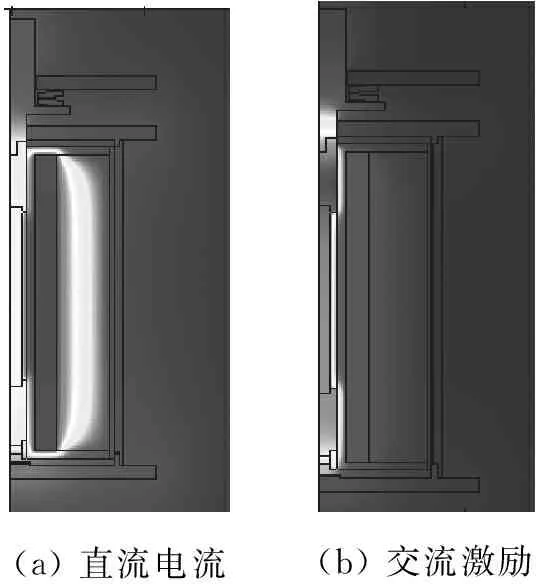
(a) 直流电流(b) 交流激励

图1 GMA温度分布

Fig.1 The temperature distribution of GMA

对线圈区域分别施加直流、交流电流，得到的GMA温度分布结果如图1所示。结果表明，当GMA工作在直流电流状态下，线圈区域的温度比GMM棒高，距离中心轴线越近的位置温度越高，温度从轴心沿径向向外逐渐降低，通电线圈焦耳热是GMA的主要发热源。当工作电流为交流时，GMM棒和上下导磁块的温度高于线圈区域，且GMM和导磁块区域的温度在径向与轴向上分布较均匀，此时材料磁滞与涡流损耗是GMA的主要发热源。

导磁块是具有高磁导率的软铁材料，工作过程中也产生一定的涡流并具有热传导作用，为明确该部件对GMA发热的影响，进行了如下分析。设置激励电流为3 A、500 Hz的正弦电流，初始温度是20 ℃、工作时间为60 s。当忽略导磁块的涡流与热传导作用时，GMA的温度变化过程，如图2所示。

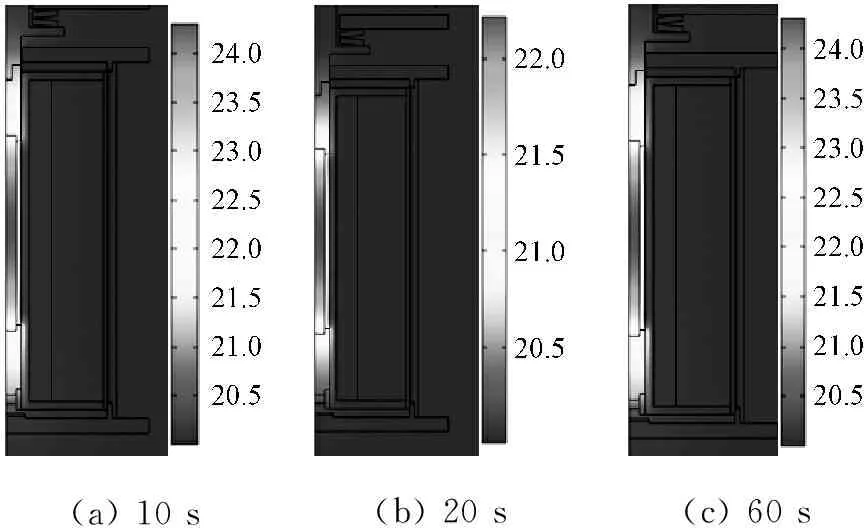
(a) 10 s(b) 20 s(c) 60 s

图2 不考虑导磁块作用的温度分布(℃)

Fig.2 Temperature distribution without consideration of the effect of a magnetic block(℃)

结果表明，GMM区域的温度最高，且具有中心高边缘低的分布特点，主要发热原因是GMM涡流热。这是由于通电线圈产生的磁场强度在中间位置最高，因而GMM中心处的涡流最大。

考虑导磁块热传导作用的温度分布结果如图3所示，导磁块的温度明显高于GMM，主要发热源是导磁块和GMM的涡流损耗作用。因此，在研究GMA的温度特性及热形变的过程中，需要考虑与GMM接触的导磁结构的涡流及热传导影响。

(a) 10 s(b) 20 s(c) 60 s

图3 考虑导磁块作用的温度分布(℃)

Fig.3 Temperature distribution considering the effect of a magnetic block(℃)

3 热形变的被动补偿方法

目前，对GMA热形变控制的方法主要有主动温控法和被动补偿法两种[16-17]。主动温控法是通过外部干预措施限制GMA的温度变化范围，进而间接实现对GMM热形变的抑制。这种方式具有较好的热形变抑制效果，但要在系统中设置温度控制装置和控制系统，因此增加了结构复杂性。被动补偿法是在智能构件温升发生后，通过在系统内部增加机械补偿装置或改变元件结构，抵消GMM的热致形变。被动补偿法的关键是在GMA设计过程中选择合适的补偿装置和内部元件。

本文设计的具有热形变自补偿功能的GMA如图4所示，其主要由GMM棒、导磁块、预压机构、输出机构、热形变补偿机构组成。核心驱动单元是圆柱形GMM，其下端固定、上端自由；通电线圈是GMM的工作磁场源，上下纯铁片、上下导磁块、导磁套筒、GMM棒组成闭合磁路，GMM工作在封闭的磁回路内。当线圈通入电流时，GMM棒在闭合激励磁场作用下发生磁致伸缩效应而伸长，其形变经过上导磁块和传递轴向外部传递。

热形变补偿机构主要由补偿套筒、下导磁块、上下纯铁片、线圈骨架、上盖构成。上纯铁片、线圈骨架、补偿套筒的上端通过螺钉与上盖固定连接，补偿套筒下端、下纯铁片、下导磁块间通过螺钉连接。其中，热形变补偿机构的上端为固定端，下端为自由移动端，自由端与底座间存在一定间隙。当线圈中通入激励电流时，GMM在激励磁场作用下会向下作用在下导磁块使补偿套筒受力，但由于GMM下端固定且补偿套筒通过螺钉和上盖固定连接，因此补偿套筒受力变形对GMA的输出位移的影响可忽略。随着GMA输出位移，GMM的温度将升高并向自由端方向产生热形变，热量将通过下导磁块传递给补偿套筒，补偿套筒因温度变化产生热膨胀而向下移动，同时会带动下导磁块和GMM向下移动。补偿套筒与GMM的热膨胀系数近似相等，二者热形变量亦相同，因此实现了对GMM热形变的自动补偿。为了保证热膨胀系数相同，同时减小对磁场分布的影响，补偿套筒的材料选择GH4169镍铬合金。

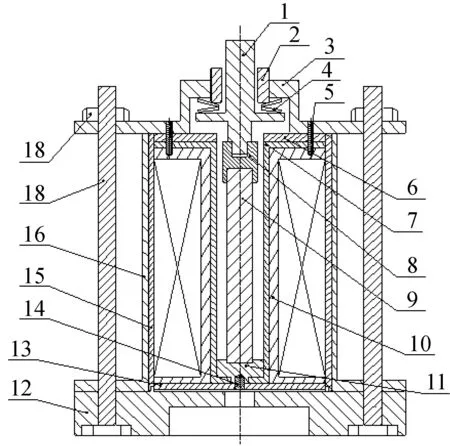
1. 传递轴；2. 预紧螺母；3. 上盖；4. 碟形弹簧；5. 螺钉；6. 上纯铁片；7. 补偿套筒；8. 上导磁块；9. GMM棒；10. 线圈骨架；11. 下导磁块；12. 底座；13. 下纯铁片；14. 螺钉；15. 导磁套筒；16. 外壳；17. 螺栓；18. 紧固螺母

(a) 二维结构图

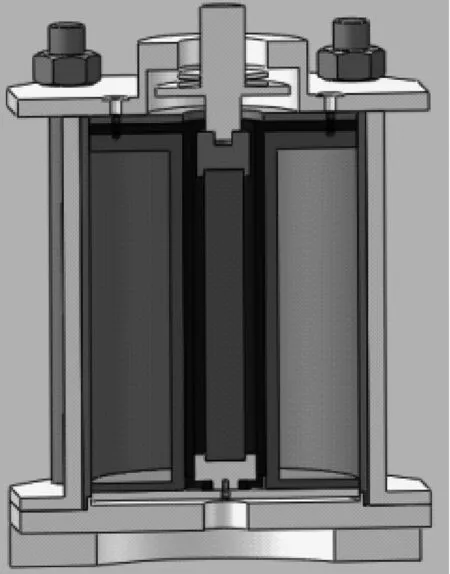
(b) 三维剖面图

(c) 实物图

研究表明，当GMM棒受到一定预压力时，磁机耦合系数能够达到最佳，GMA具有更大的输出位移[18]。传递轴、预紧螺母、上盖、碟形弹簧构成了预压机构，通过调节预紧螺母与上盖间的螺纹配合长度，便可调整碟形弹簧对GMM所施加的预压力大小。

4 实验与讨论

本文研制的GMA中所涉及的GMM是正磁致伸缩材料TbDyFe，实验系统如图5所示。NF双极性可编程电源为GMA提供工作电流，能够输出交流、直流叠加形式的电流，可利用这种激励形式消除倍频对输出特性的影响；输出位移通过MTI高精度激光位移传感器测量，精度为0.01 μm；通过粘贴在GMM棒和线圈内壁上的温度传感芯片，监测GMA温度变化；利用粘贴在GMM上端的电阻应变片测量预压力，并通过YE3817C型应变放大器实时读取应变值。

图5 GMA综合性能测试系统

4.1 模型验证

为了验证模型对GMM应变的描述能力，分别在有、无预紧力作用下对GMA位移进行分析。首先选取插值基函数对GMM棒的输出位移进行多项式插值，并用插值函数uh(x,t)近似表示输出位移u(x,t)。再通过将插值函数融入到致动器动力学波动方程中，得到位移、速度、加速度间的二阶微分方程。然后，采用Newmark方法解非线性动态微分方程，得到代数计算迭代格式，再根据已知的加速度，进而求得速度和位移及应变(计算过程中的磁化强度及GMM棒应力计算方程参照文献[10]中的式(13)及(24))。模型求解的流程图如图6所示，计算模型中的部分主要参数，如表1所示。

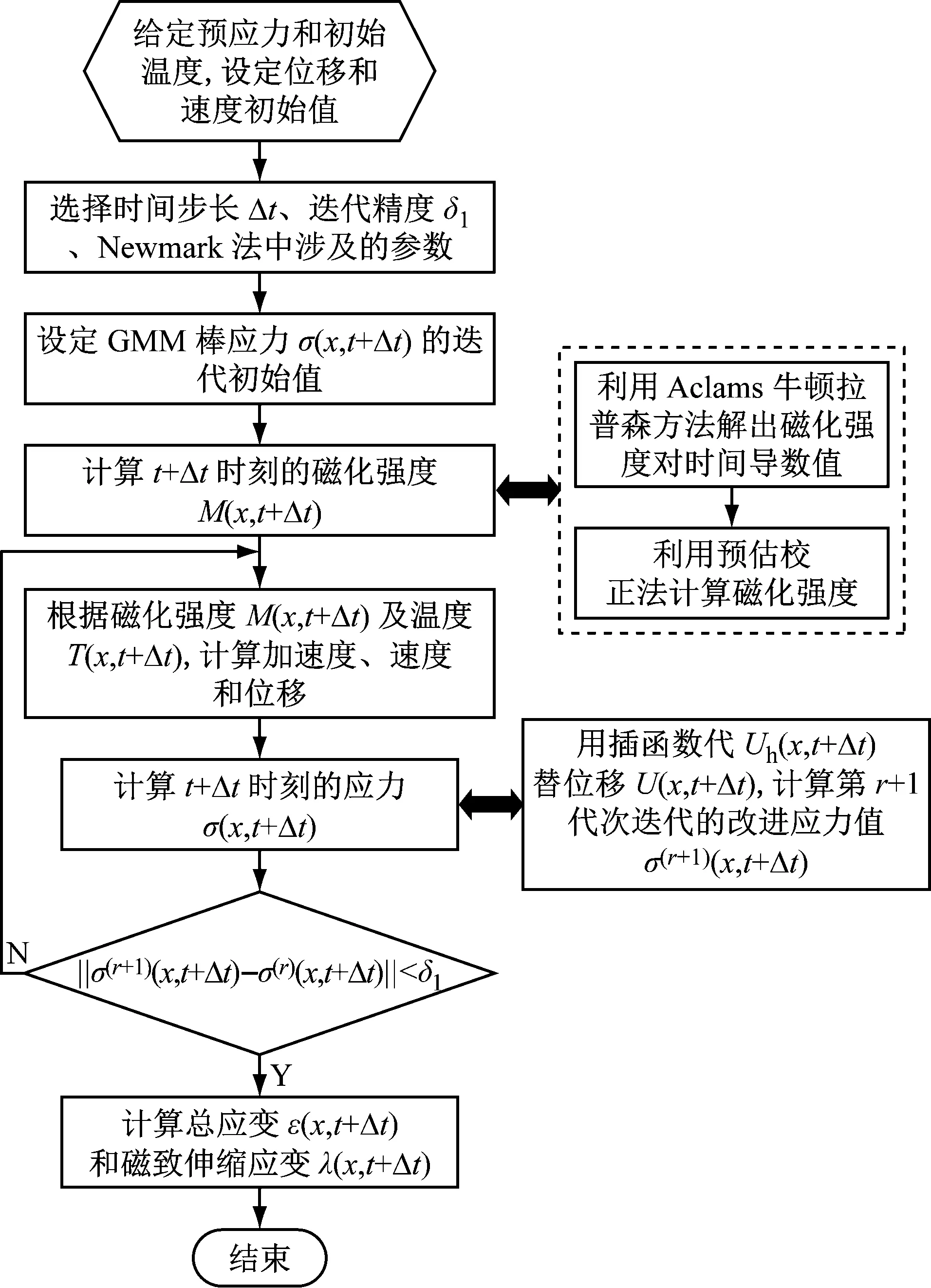
图6 模型求解流程图

表1 模型中的部分主要参数

在无预紧力和18 MPa预紧力条件下，对GMA施加2 A、500 Hz的简谐电流，同时测量输出位移，位移测量值和预测结果如图7所示。结果表明，GMA以相同频率输出简谐规律变化的位移；无预紧应力时，位移幅值约为45 μm；预应力18 MPa时，位移幅值约为69 μm。这表明，适当的预紧力可改善GMA的输出特性。位移的预测值与实测值吻合度较高，位移预测的平均相对误差分别约为6.2%和8.9%，相位有微量超前。

向GMA分别施加准静态及1 000 Hz、-20～20 kA/m的磁场，通过计算GMM的应变分析磁滞特性，结果如图8所示。在升程与回程过程中应变存在磁滞，且随频率增加磁滞增大。在GMM的不可逆磁化过程中，磁畴发生能量损失并引起磁滞，磁滞能量损耗是温升的重要原因之一。

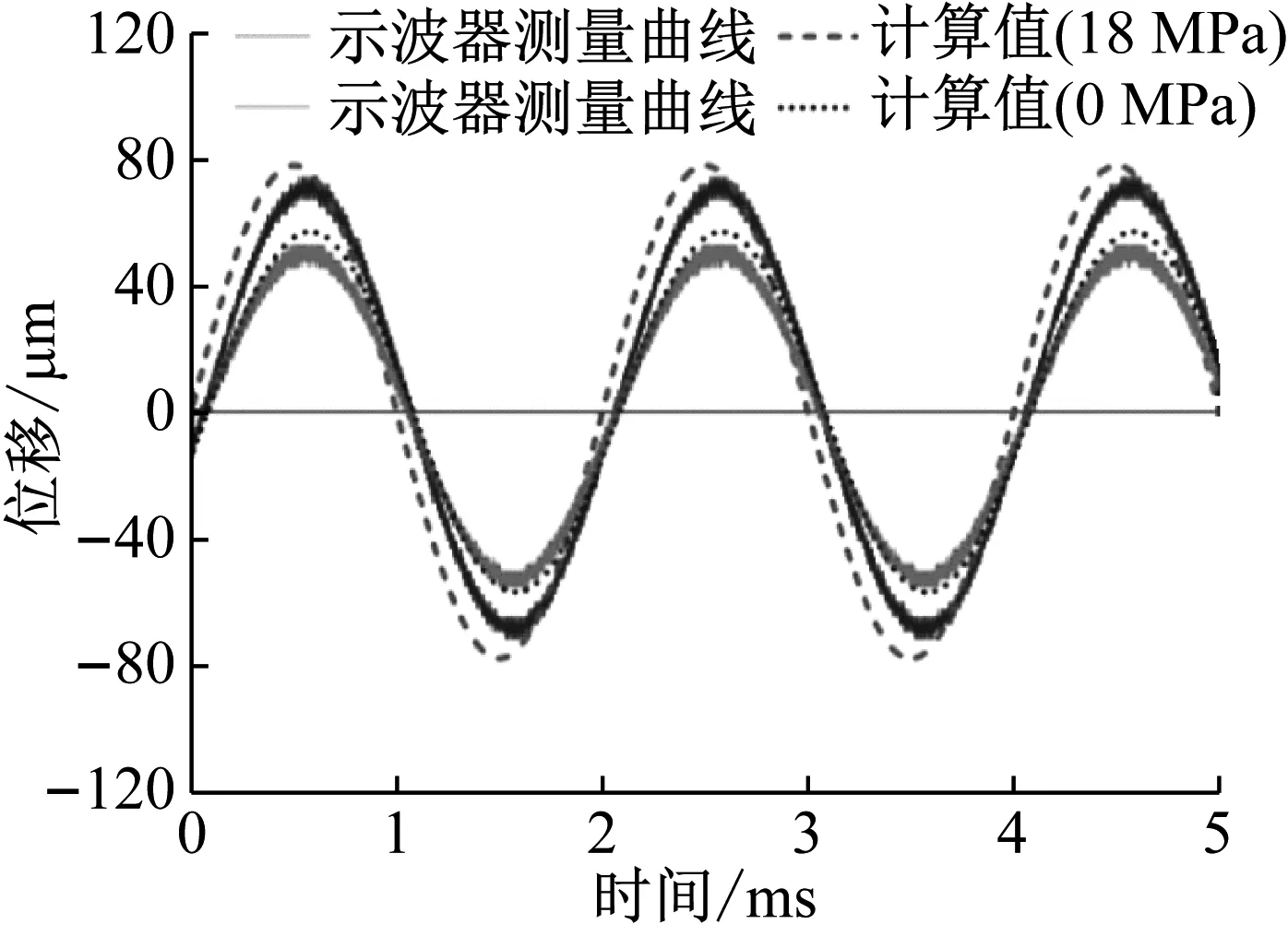
图7 GMA输出位移的理论值与实测曲线

图8 GMM的形变回线

为了分析力磁耦合对GMM应变的影响，研究了在不同预压力(0 MPa、18 MPa)和直流激励(0～2 A)下GMA的位移输出特性，实验结果如图9所示。结果表明，在相同预压力作用下，随着激励电流的增加，GMA的输出位移迅速增大，但与激励电流间并不是完全的线性关系。对GMA施加18 MPa的预压力，相比于0 MPa的预压力来说，GMA的输出位移有了很大提高，但当电流继续增大时，GMM材料都达到饱和状态，GMA的输出位移增幅变小。

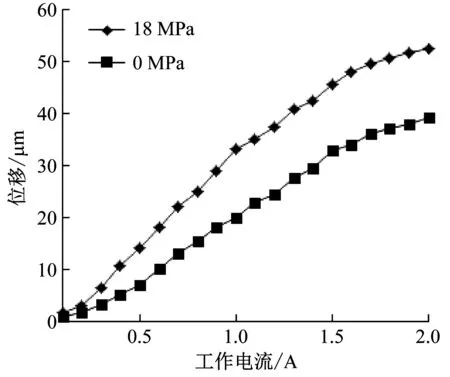
图9 不同预压力和电流作用下GMA的位移变化

4.2 静态与动态激励下的温度特性

根据有限元分析结果，当工作在直流状态时，线圈为GMA的主要热源，因此在线圈骨架内壁的中间位置处贴置温度传感芯片。工作电流分别为0.5 A、1 A、1.5 A、2 A、3 A，工作时间为25 min，起始温度为20℃，在此条件下测量了GMA在不同驱动电流作用下的温升，得到了静态驱动电流对温升的影响结果，如图10所示。施加25 min的3 A电流后，GMM的最高温度达到了约28 ℃。继续对3 A电流通电到150 min，在实验过程中对同组实验进行多次测量并取平均值，结果如图11所示。随工作时间的增长，GMA的温度呈现逐渐增高的趋势，当连续通电120 min后，平均温度达到87.4 ℃；在120～150 min内，GMA温度变化微小，基本不再继续升高，此时达到了热平衡状态。

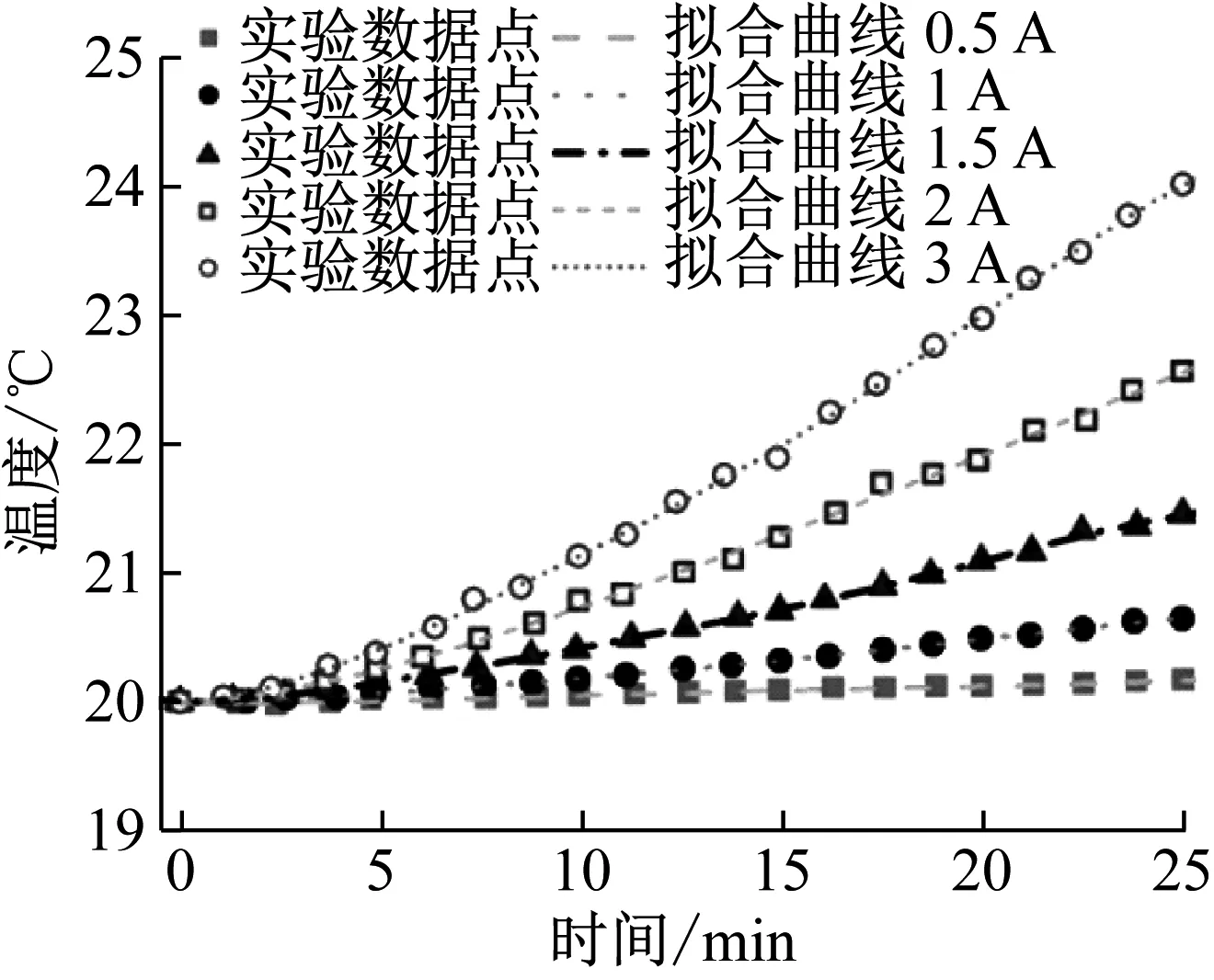
图10 不同电流下GMM的温度变化

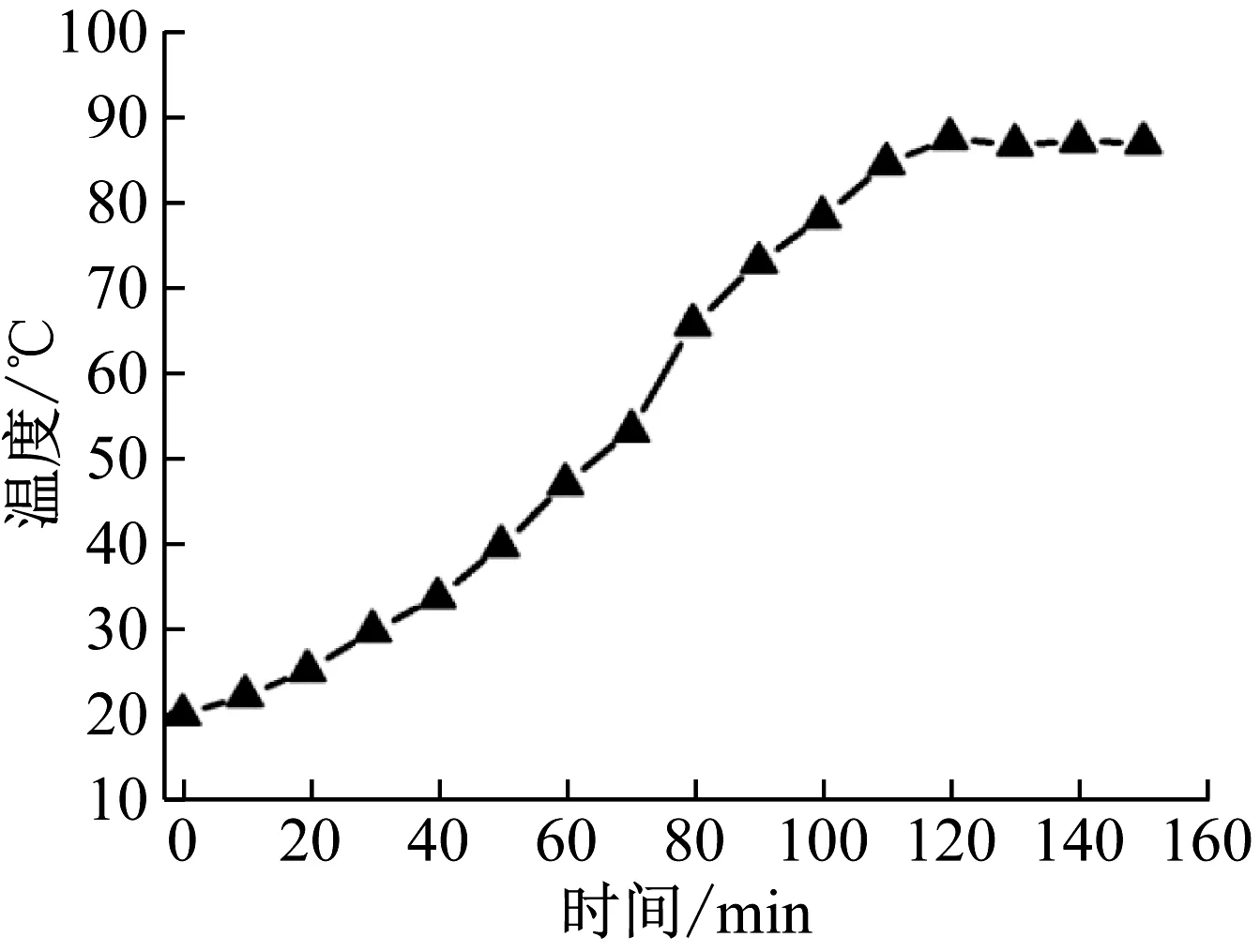
图11 GMA的温度变化(恒定直流激励)

分别在GMM棒和线圈内壁的中间位置处贴置温度传感芯片，实时测量动态激励磁场作用下的GMA温度变化。首先，向GMA施加不同频率的交流激励，电流幅值2 A、频率分别为0 Hz、200 Hz、500 Hz，工作时间为60 s，GMM的温度变化曲线如图12所示。当频率为500 Hz时，温度达到了38.7 ℃，与初始温度相比升高了18.7 ℃。而在0 Hz时温度为20.5 ℃，仅升高0.5 ℃。结果表明，GMM在不同频率下表现出的涡流损耗特性不同，因而导致其温升特性也不同。工作频率越高，GMM产生的涡流效应越强，温升速度越快，温度变化越大。

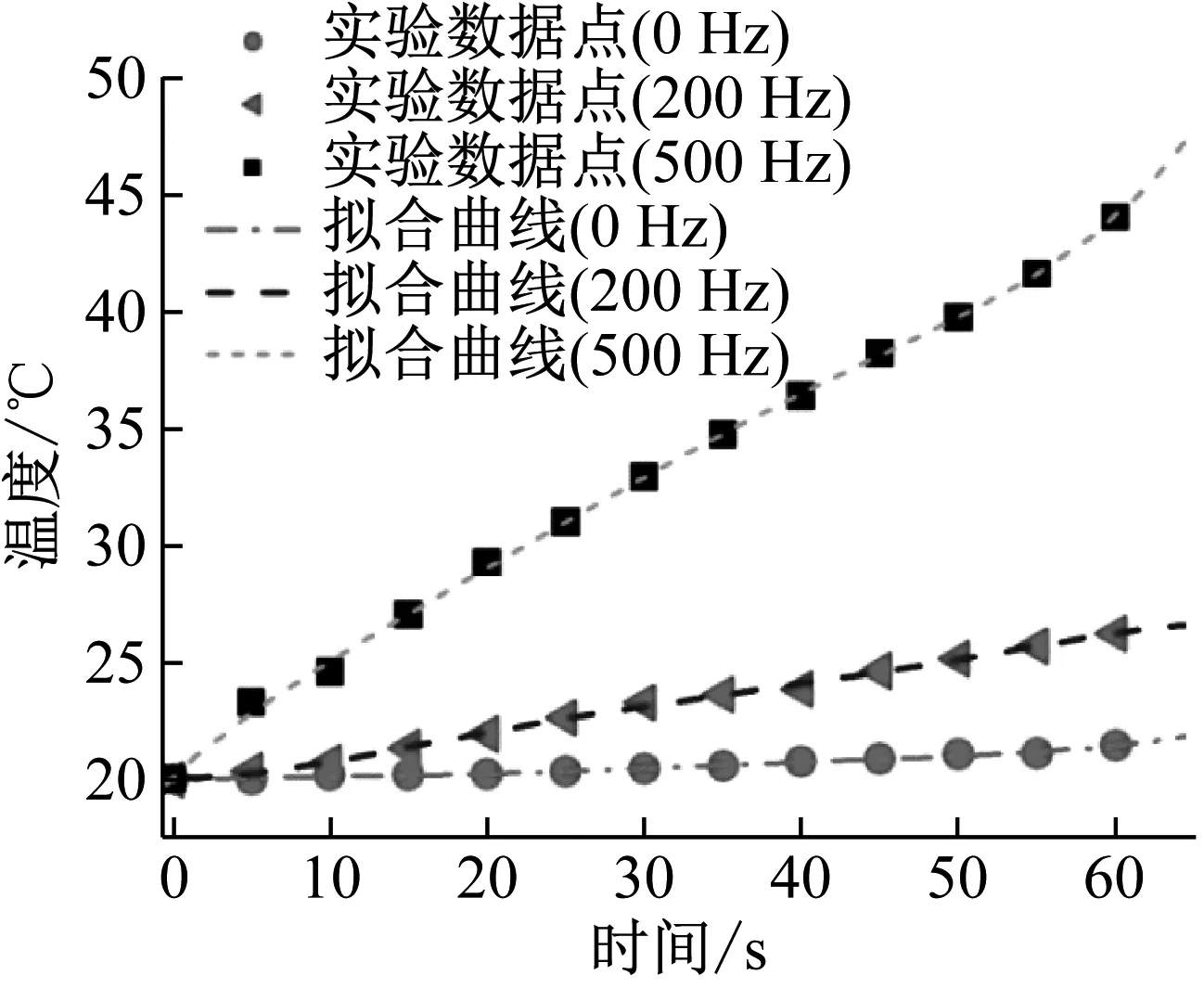
图12 GMM的温度变化(动态交流激励)

在相同条件下对线圈区域施加激励，线圈和GMM初始温度分别为20 °C和24 °C，测得GMM棒和线圈的平均温度随频率变化的曲线如图13所示。结果表明，随着频率的增加，线圈和GMM区域内的温度都逐渐升高，且GMM的温升速度比线圈快；当频率低于150 Hz时，线圈温度高于GMM棒，此时线圈为GMA的主要发热源；当频率大于150 Hz时，GMM棒的温度高于线圈区域的平均温度，GMA温升主要由GMM棒自身涡流特性及磁滞损耗而产生。因此，当工作在高频状态时，不可忽略GMA的温升，需要采取相应的热形变补偿与控制方法。

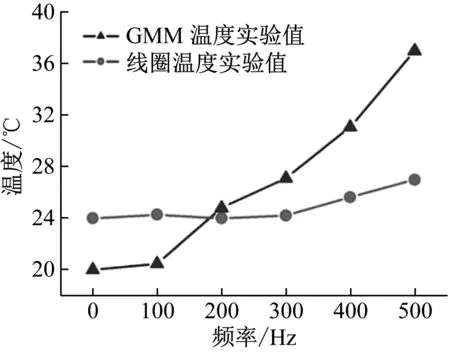
图13 GMA温度随工作频率的变化

4.3 热形变补偿实验

在保证激励电流和工作时间等工作条件相同的前提下，对本文设计的带有热形变自补偿功能的GMA(1号GMA)与无补偿结构的GMA(2号GMA)进行了实验。通过实时检测输出位移，并与初始位移比较，分析热形变的补偿结果。位移变化如图14所示，2号GMA中的GMM产生了较大的热形变，且热形变很大程度影响了GMA输出位移，致使输出位移随着温度的升高一直增大。1号GMA的输出位移基本恒定不变，仅当温度高于某个值后，位移出现微量减小。这是因为温度变化影响了GMM的磁致伸缩系数，当温度较低时，对磁致伸缩系数影响较小；当温度较高时，磁致伸缩系数明显减小，降低了GMM的磁机转换效率，因此磁致伸缩形变减小，导致了GMA总输出位移减小。综合上述分析，具有热形变补偿机构的GMA能够在较低频率时，完成对温升产生的热形变自动补偿。但是，所研制的GMA工作频率范围较窄，需要进一步优化其结构，并对其进行高频热形变自补偿功能的实验测试。

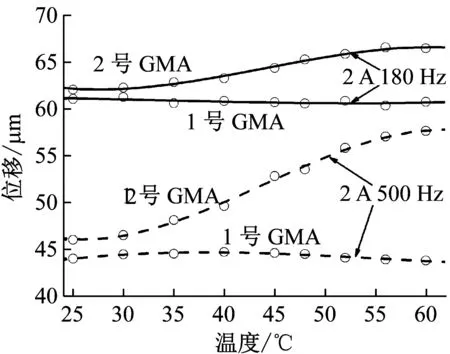
图14 GMA位移热补偿对比图

对2 A、500 Hz交流激励下的GMA进行补偿误差分析，所得到的结果如图15所示。结果表明，随着温度的不断升高(温度增大于45 ℃)实验补偿值曲线与理论热膨胀曲线距离明显增大。温度25 ℃时实验补偿值为2.3 μm，理论热膨胀值为2.5，补偿误差率为8%；温度45 ℃时实验补偿值为11.4 μm，理论热膨胀值为12.5，补偿率误差为8.8%；而在温度50 ℃和60 ℃时补偿率误差分别为9.4%和 12%。以上数据说明该种补偿方式中低温(45 ℃以下)补偿效果要好于高温补偿效果。

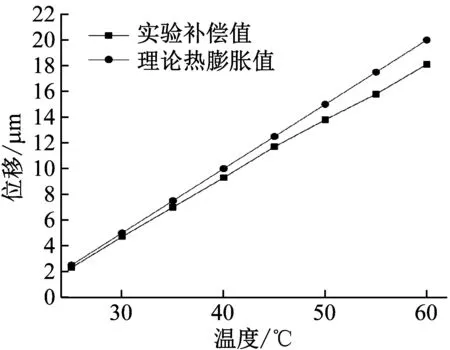
图15 补偿位移与理论热膨胀值对比图

5 结 论

(1) 通过将GMM的纵向应变分解为应力、磁场、温度单独作用的应变以及三场耦合作用的应变，推导出了考虑温度影响的GMM多场耦合应变模型，并完成了对GMM热形变的数学描述，其包括热膨胀线性应变和热磁耦合非线性应变两部分。

(2) 通过对GMA内部温度分布特性的分析，明确了发热源、温度变化与频率间的关系。当工作在直流状态时，GMA的温度随工作时间逐渐增高，最后达到热平衡；当工作在交流状态下，低频时线圈为GMA的主要发热源，高频时的温升主要由GMM的涡流特性及磁滞损耗产生。

(3) 根据长度和热膨胀系数相同，热形变亦相近的原理，设计了GMM热形变被动补偿机构，研制了具有热形变自补偿功能的GMA。实验结果表明，具有热形变补偿机构的GMA能够对温升产生的热形变自动进行补偿。