多跨连续梁桥多子结构协同混合试验方法研究

杨剑峰， 田石柱

(苏州科技大学 土木工程学院， 江苏 苏州 215011)

结构抗震混合试验方法是将数值模拟与试验加载两种分析方法相结合，从而更加经济合理地还原结构在地震下的真实响应的一种新型试验方法。近几年，几十公里长的海湾、海峡特大桥等宏伟工程的完成，桥梁结构规模越来越大，结构体系越来越复杂，故现代大跨桥梁建设对桥梁的抗震性能提出了越来越高的要求，这同时给结构抗震试验研究带来了巨大挑战[1]。由于这些结构在强震作用下容易出现分布式破坏特征，故抗震混合试验中传统的数值积分算法不能很好的适应混合试验系统分布式复杂化的发展，进而很难进行大型复杂结构的抗震混合试验[2]。

随着计算机与网络技术的飞速发展，土木工程结构试验出现了网络化的发展趋势，如Peer-to-Peer等混合试验系统[3-4]，即利用不同实验室设备对多个子结构进行同步试验加载，借助网络进行数据交互，降低了试验成本，进而形成近十年来受到越来越多国内外研究者重视的多子结构混合试验[6-8]。其中，杜雨峰等[9]利用多个有限元程序的各自优势，采用混合试验方法对一SRC框架剪力墙混合结构进行了地震响应模拟，并取得了较为满意的试验结果。

为了进一步地解决强震作用下大型结构数值子结构地震响应精度对整体试验精度的影响，许国山等[10]将有限元软件Open SEES引入混合试验中以提高数值子结构的模拟精度。为避免数值子结构采用简单线性模型给试验结果带来影响，王涛等[11]提出了模型更新的方法以实时更新数值子结构模型参数；而混合试验中采用预测-修正思想的数值积分算法一般可以较好地避免试验子结构对加载路径敏感的问题，故王涛等[12]为了进一步提高算法的精度，通过对传统神经网络算法的改造，提高了在线预测数值子结构恢复力的精度与计算效率。

为了提高混合试验的适应性，提高试验协同处理多个子结构的计算精度与分析效率，本文首先介绍基于Newmark-β法的预测-几何修正(Predicting and Geometry-Correcting)算法的基本思路；其次，依托P-GC算法，根据桥梁结构特性建立多子结构协同混合试验系统；最后对某实际多跨连续梁桥进行数值模拟试验，并与全桥有限元计算结果进行对比分析。

1 P-GC积分算法基本思路

P-GC算法针对混合试验中子结构多的特点，将算法分析模块分为两个阶段：预测阶段与修正阶段。在预测阶段，为了逼近下一步实际运动量，采用考虑结构实时信息的动力平衡方程进行运动量的预测。建立整体结构的动力增量平衡方程与2个Newmark-β积分算式：

(1)

(2)

(3)

这里与M-PC算法[13]预测方法的不同在于预测刚度Kn采用前一步的过程刚度，而不是初始刚度；且无论是有限元分析还是物理试验加载，当结构分析步正处于结构响应往返交接点处时(速度变向)，会造成此时得出的刚度出现跳跃即偏离实际曲线或称之为力-位移曲线滞后[14]，常规方法是在tn与tn+1之间采用更小的时间步积分。为了避免迭代积分，本文提出的P-GC算法根据刚度退化特征利用初始刚度对过程刚度进行修正。即当结构处于滞后点处时，所得的过程刚度显然偏小，由于结构出现强非线性后会存在位移差值幅度大于力差值幅度特征，故此刻的过程刚度不可作为下一步的预测刚度，而是利用初始刚度作为下一步的预测刚度，实现大刚度小位移调整，以减小误差；越过往返点之后，继续采用前步过程刚度作为下一步的预测刚度进行位移预测。

在修正阶段，为了提高计算效率，不再考虑整体结构的动力平衡方程，可避免因采用不准确的刚度所带来的分析误差。子结构动力平衡方程如下式：

[m]{a}+[c]{v}+f=P

(4)

式中f为子结构系统的恢复力。将式(4)按内部节点与边界节点分块表示得：

(5)

由式(5)可得子结构边界力{R}与边界位移{dex}、速度{vex}、加速度{aex}之间的关系。多子结构拆分示意图，如图1所示。

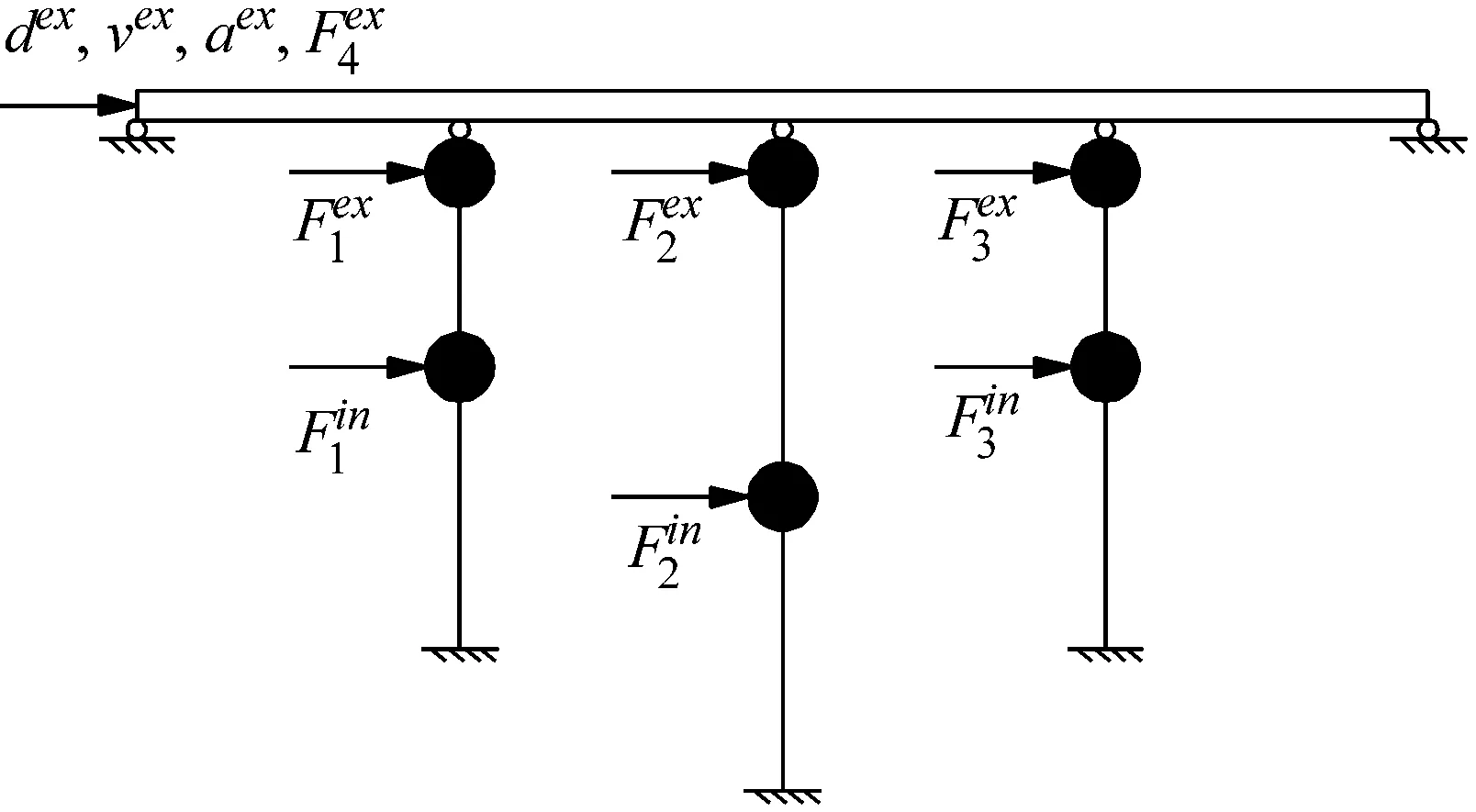
(1) 整体结构

(2) 整体结构拆分

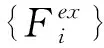
多子结构边界的协调与平衡应满足下式：

(6)

(7)

(8)

定义几何修正：

(9)

(10)

(11)

式中:α可以采取初始值，也可以动态选取，其值代表修正幅度，取决于精度需求。由于质量矩阵、阻尼矩阵、刚度矩阵线性段是已知的，又由于加速度、速度、位移存在一个量纲比值，根据式(10)，α一般在某一量纲值附近跳跃。其主要思路就是利用本步预测位移加载获得的结构刚度信息更新α，在本步修正阶段假设α保持不变，从而进行丢失位移的几何修正。P-GC算法示意图及算法系统框架，如图2、3所示。

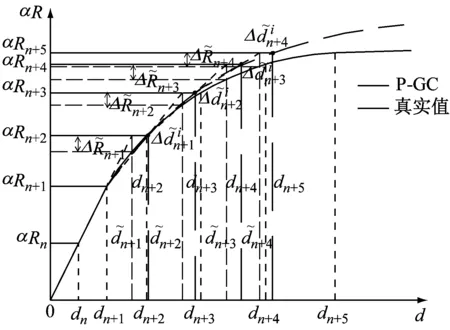
图2 P-GC算法

这里，P-GC算法采用几何修正方法修正位移增量，即根据力的平衡原则将预测阶段所得的不平衡力值几何等效转化为所丢失的预测位移增量值；倘若结构易出现强非线性，即可利用强非线性的位移差值幅度远大于力差值幅度特征，将修正位移分多步加载，进一步逼近准确值，直至力平衡。这一方法实现了根据精度需要来寻找丢失的预测位移增量值，且不会出现往返加载，成功避免了试验子结构对加载路径敏感的这一问题。

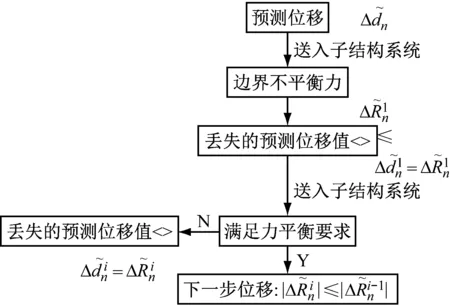
图3 P-GC算法系统架构

2 基于P-GC算法建立桥梁多子结构协同混合试验系统

本文依托P-GC算法思想，将整体结构中拆分出来的计算子结构与试验子结构平等地视为独立的子系统，每个子结构在自己的子系统中接受同等的处理方式，故不需要建立整体结构的运动方程，只需建立对应子结构的运动方程，独立地进行数值计算或试验加载。

而桥梁结构的分析难点在于支座处的模拟。针对大跨桥梁多使用盆式橡胶支座，根据其使用性能定义[15]：以图4所示桥梁为例，主梁悬臂端支座定义为无摩擦滑动支座；中墩顶部固定支座定义为固定铰支座，两个边墩顶部滑动支座定义为带有初始刚度的弹性连接(盆式橡胶支座的有限元模拟，本模型采用TRANSLATOR模型模拟。示意图如图5所示。TRANSLATOR模型可进一步定义阻尼等连接属性，能够真实地模拟盆式橡胶支座的力学性能，比之通常所用的弹簧单元模拟更加合理)。

图4 整体结构拆分后的计算简图

则子结构边界力平衡与位移协调应满足：

(12)

(13)

定义边墩支座顶部位移d0，支座滑动值di0，边墩顶的位移di。边墩的振动形式有以下六种(如图6所示)。根据对称性原则，边墩位移主要满足以下三种情况：

(14)

而三种位移在所属边墩子结构内满足动力平衡方程：

m(an+ag)+cvn+kndin=kzn(d0n-din)

(15)

其中kn为子结构抗侧刚度，kzn为对应支座水平滑动刚度。根据式(12)，定义：

(16)

进而得出位移协调下的力平衡判断公式：

R0+R1+R2+R3=-(m0+m1+m2+m3)ag

(17)

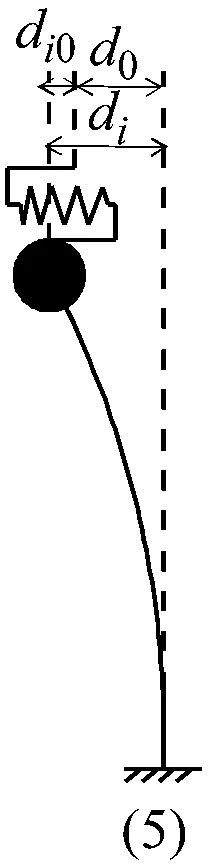
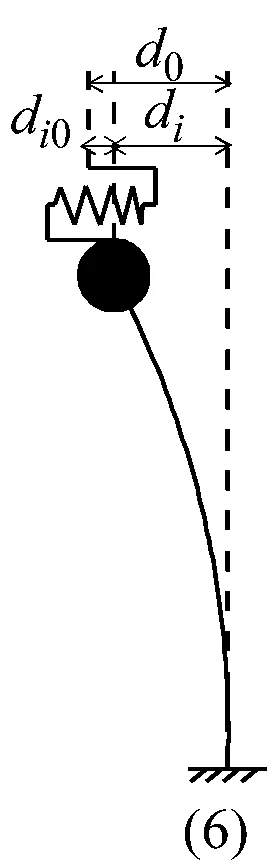
图6 边墩的六种振动形式

Fig.6 Six forms of the side pier vibration

由于中墩与边墩同主梁的连接方式不同，桥梁振动的主振型由中墩和主梁的固结来控制，故称之为主自由度；而边墩由于和主梁滑动连接，在桥梁主振型控制下，存在子结构自我模态振动，故称之为次自由度。多跨连续梁桥多子结构协同混合试验系统，如图7所示。

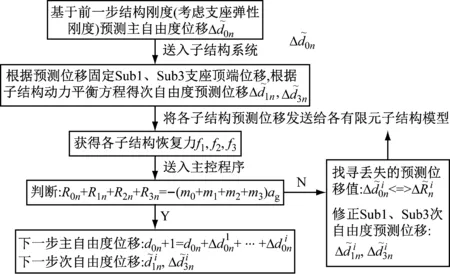
图7 多跨连续梁桥多子结构协同混合试验系统

子结构次自由度预测方程如下：

第n步

m(an+agn)+cvn+kndin=kzn(d0n-din)

(18)

第n+1步

m(an+1+agn+1)+cvn+1+kn+1din+1=

kzn+1(d0n+1-din+1)

(19)

则n步的动力增量方程为：

m(Δan+1+Δagn+1)+cΔvn+1+kn+1din+1-kndin=

(kzn+1d0n+1-kznd0n)-(kzn+1din+1-kzndin)

(20)

假设kn+1和kzn+1基于前一步不变，同时建立Newmark-β积分算式，则上式转化为：

mΔan+1+cΔvn+1+Δdin+1(kn+1+kzn+1)=

-mΔagn+1+kzn+1Δd0n+1

(21)

Δdin+1=Δtvn+0.5Δt2an+βΔt2Δan+1

(22)

Δvn+1=Δtan+ΔtγΔan+1

(23)

即得次自由度预测运动量的值。

系统中边界协调计算模块作为主程序，主要包含了三个子模块：边界协调与平衡算法模块、传递有限元接口数据模块、获取子结构恢复力模块。主程序用MATLAB编写。协调主程序结构，如图8所示。

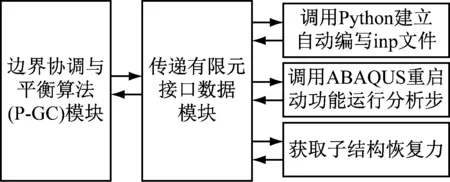
图8 协调主程序结构图

有限元接口模块，即ABAQUS前后处理的二次开发都由Python语言编辑。为提高分析效率，每一个子结构对应一个有限元接口模块。这里通过局域网技术将所有的分析计算机连接到主控计算机，形成星型网络拓补结构，如图9所示。

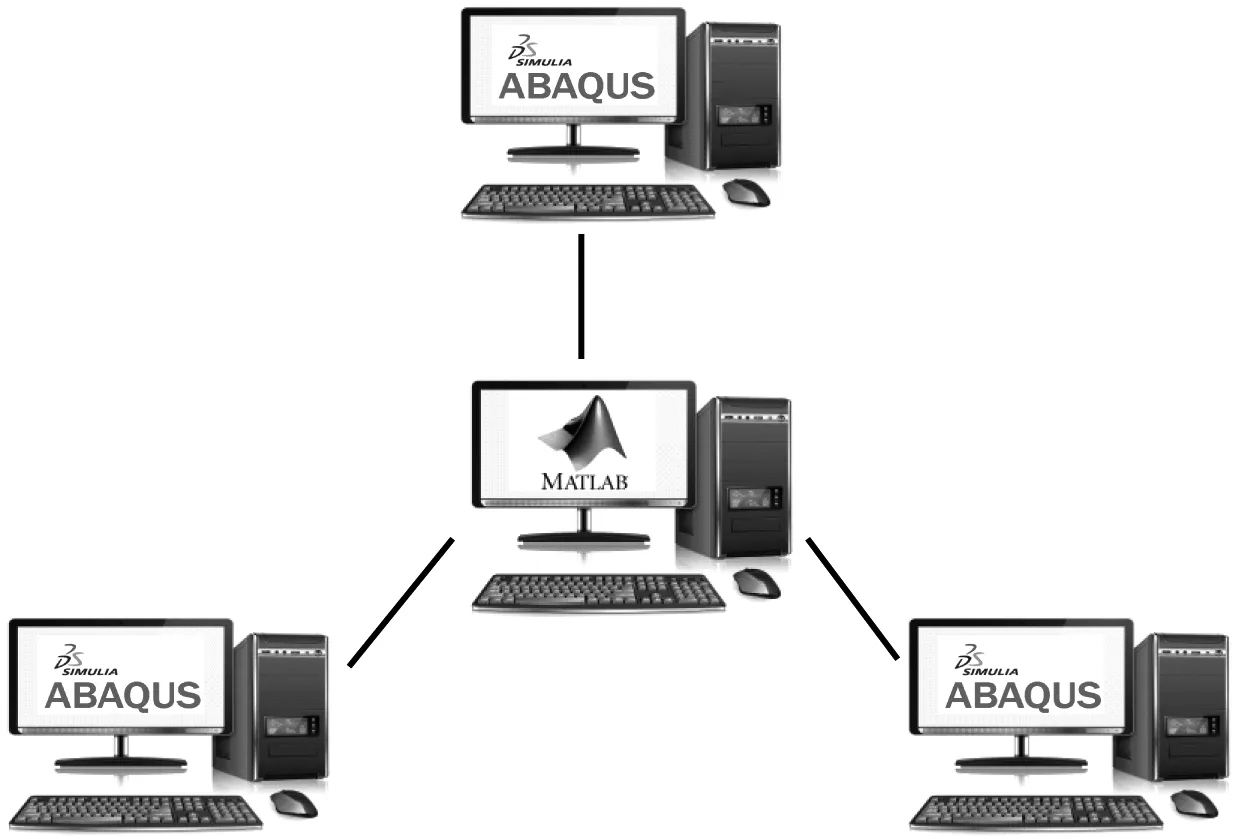
图9 多子结构联机协同混合试验架构

3 多跨连续梁桥数值模拟试验

3.1 工程概况

某多跨连续梁桥全长285 m，第一联桥型布置为 (30+2×50+30)m预应力混凝土连续梁，抗震设防烈度为7度。本桥作为城市主干路，根据《城市桥梁抗震设计规范》属于丙类桥；场地基本地震加速度为0.1 g，故定义E1作用为0.046 g，E2作用为0.22 g。

本试验选取了6个工况进行分析，见表1。桥梁总体布置图见图10。

表1 计算工况

图10 桥梁总体布置图

表2列出了全桥模型前10阶振型及自振频率。

3.2 模拟试验结果分析及与全桥有限元分析结果对比

(1) 7度E1作用

表2 全桥模型前10阶振型及自振频率

试验结果同样证明了TRANSLATOR模型很好的模拟了支座运动特性，且P-GC算法较好的解决了主次自由度的边界协调问题。

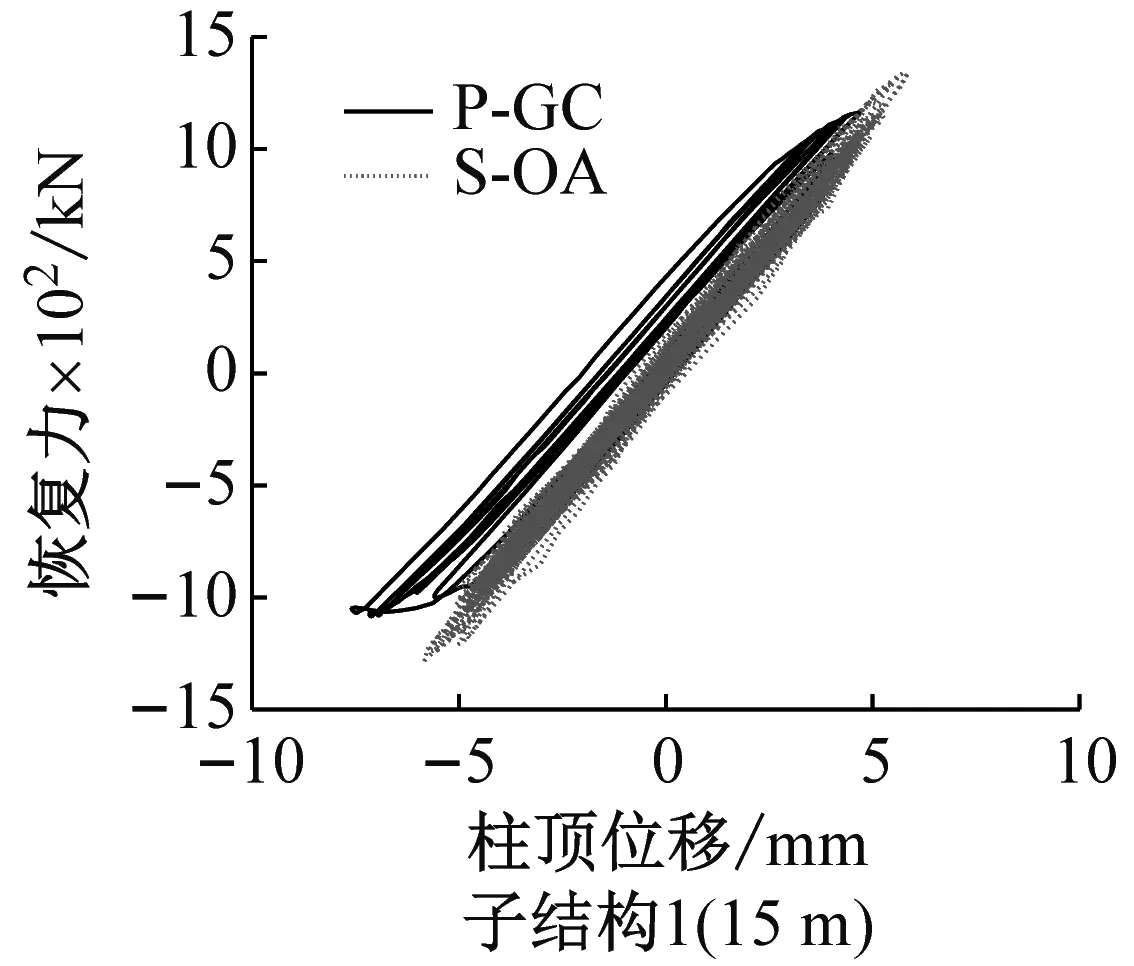
(1) 子结构1(15 m)

(2) 子结构3(15 m)

图12 3～9 s墩顶位移时程极值对比图

Fig.12 Contrast diagram of extreme values of displacement time curve for piers

由图11～13可知，在7度E1作用下本桥不管是有限元分析还是协同混合试验分析，都是处于线弹性阶段，故本桥设计满足7度E1设防要求。其中，由于在整桥分析时主梁的联结作用被完全保留，故边墩刚度较混合试验分析结果略大；而中墩与主梁的连接作用被精确保留，故两种方法的分析结果几乎一致，这也证明了多子结构协同混合试验方法具有较好的精确性和稳定性。

(2) 7度E2作用

由于Taft波作用下两种分析方法均表明结构破坏，故只取El-Centro波和人工波分析。由图14可见，在7度大震作用下，中墩不再一直是整体结构的主要抗力构件，两个边墩的地震响应也随之增大，并有超过中墩的趋势。这是由于边墩的抗侧刚度较中墩大，在大震作用下，中墩屈服后，边墩随即变为主要抗侧力构件，并随着中墩也开始屈服，结构已然呈现出分布式破坏。由于本文方法只考虑了水平自由度的平衡与协调，对中墩进行强非线性分析时，由于两种方法采用的动力质量模型不一致，故两种方法结果存在一定差异。

4 结 论

本文提出了基于Newmark-β法的预测-几何修正算法，并根据此算法开发了适用于桥梁结构的多子结构协同混合试验系统，并通过某实际多跨连续梁桥数值模拟试验对系统进行了验证。主要结论如下：

(1) 本文提出的P-GC算法推进了抗震混合试验方法更好的模拟结构在地震下的真实响应；通过混合试验结果与有限元结果对比，在结构线性阶段，证明了多子结构协同混合试验方法具有较好的准确性和稳定性；在结构非线性阶段，多子结构协同混合试验方法可以较好的避免有限元动力分析方法带来的响应结果波动性，并考虑了结构刚度退化后的影响。

(2) 本文提出的P-GC算法利用结构强非线性的位移差值幅度远大于力差值幅度特征，将修正位移分多步加载，可进一步逼近准确值，直至力平衡。这一方法实现了根据精度需要来寻找丢失的预测位移增量值，且不会出现往返加载。

(3) 本桥在7度E1作用下，抗震性能良好，结构保持弹性；而在7度E2作用下，本桥中墩首先进入屈服，进而边墩也随之屈服，呈现出分布式的破坏特征。由于支座尚未完全破坏，故连续梁桥在考虑大震作用时，不能只关注固定墩的抗震设计，活动墩的抗震设计与加固同样重要。

(4) 本文提出的P-GC算法需要建立结构初始状态矩阵，所以结构的质量模型与初始刚度将影响到算法的精确性。故需要根据结构的质量分布特性，结合模态分析，对多子结构协同混合试验系统的初始信息进行调整，从而可以进一步提高系统分析的准确性与适应性。

(5) 本桥的多子结构协同混合模拟试验的成功为未来的物理试验的设计与研究提供了很好的理论支撑与计算平台，实现了结构抗震混合试验的信息化与网络化的发展目标，进一步提高了抗震混合试验方法在研究结构抗震性能方面的适用性。