浅谈如何培养初中生的数学思维能力
毛行永
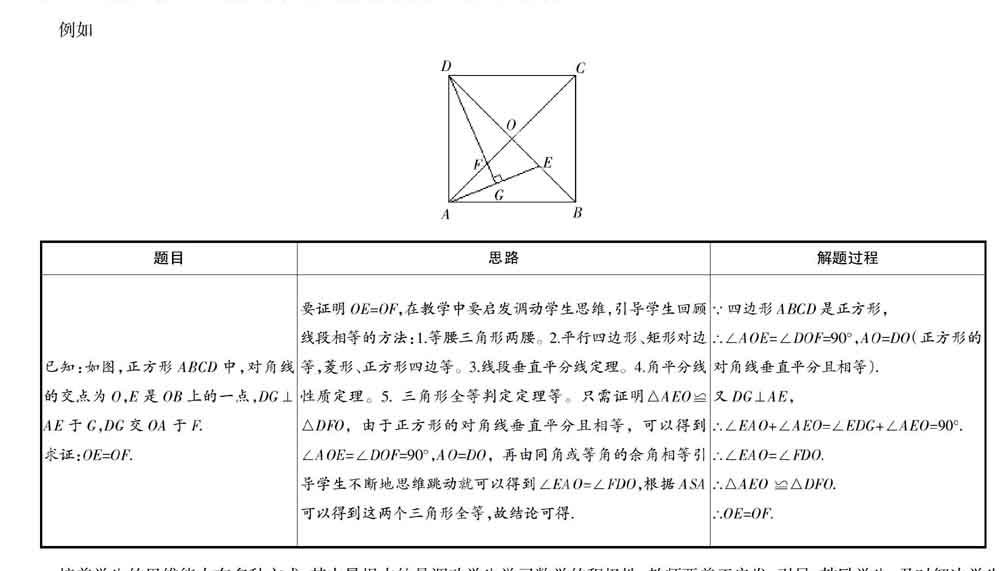
“数学是锻炼思维的体操。”所谓数学思维,就是根据一般的思维规律来认识数学对象的本质属性及其内在规律(例如空间形态、结构关系、数量关系)的理性活动。新课程标准指出数学课程的基本出发点,即义务教育阶段是促进学生全面发展的阶段,它要考虑数学本身的特点,遵循数学的本质,引导学生理解数学的本质属性和内在规律,逐步掌握并学会应用。然而,长期以来,学习方法的缺乏,目标的判定不当,以及在思维惯性问题上遇到的困难严重制约了学生的有效思维并阻碍了学生在数学中思考。
为了解决这些问题,我提出了以下看法。
一、调动数学思维能力
1.合理设置学习目标,激发学生积极性
要建立符合新课程标准的学习目标,根据学生的学习条件,建立良好的师生关系,使学生放松积极地参与课堂教学。在教学中创设问题情境时,教师应注意引导学生的思维方向。提出的问题应该是简单且具有层次性和针对性的,善于启发学生的思维,但又不超过学生的认知水平。教师在教学中要主动指出学习的中心目标,引导学生多角度思考问题。例如我在教学“数轴”时,设计了如下程序:
例:数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上任意画一条长为2009厘米的线段AB,则线段AB盖住的整数点的个数是多少?
分析:本题中计数方法是易错点。这道题应从分类讨论的数学思想方法中体会。
点拨:考虑线段AB的端点是否与整数点重合?
解:(1)若线段AB的端点与整数点重合,且数轴的单位长度是1厘米,则线段AB盖住2010个整点;(2)若线段AB的端点不与整数点重合,且数轴的单位长度是1厘米,则线段AB盖住2009个整点;综上,应是2009或2010.
通过这个问题的定向解决,大多数学生能够掌握数轴的特点,接受良好的思维训练。又如:a取什么值时,关于x的方程a(a-2)x=4(a-2),1.有唯一的解?2.无解?3.有无数多解?4.是正数解?
分析:考虑未知的系数a是否为0.
思想方法:从一元一次方程ax=b的解的情况出发考虑:
解:1.当a不等于0且a不等于2时,方程有唯一的解,x=4/a
2.当a=0时,原方程0x=-8,无解
3.当a=2时,原方程0x=0,有无数多解
4.由1可知当a不等于0且a不等于2时,方程有唯一的解,x=4/a,所以只要a与4同号,即当a>0且a不等于2时,方程的解是正数。
含参数方程必须对参数进行讨论。
除了定向思维训练外,我更注重加强学生逆向思维、横向思维、垂直思维、多向思维训练。应用教学大纲是培养学生思维能力的有效途径,培养学生从不同角度思考,根据实际情况提出可以解决的问题。渐进式学生综合解决方案,从一种方法到多种解决方案,体现了思维训练的渐进性。在老师的指导下,学生会逐渐学会思考,这种思维训练无疑可以帮助学生培养良好的数学思维习惯。
2.开展丰富课堂活动,发展学生思维能力
开展内容丰富、开放的课堂活动,可以使学生发挥个性,积极专注地思考,带动课堂氛围,从而有效地激发学生的思维潜能,长此以往,学生在逐渐爱上这种开放热烈的课堂的同时,也会形成良好的思考习惯。老师在教学中应逐步向学生传授观察、比较、分析、综合、抽象、概括等思维方法。例如,我在教授平面直角坐标系时设计了一个这样的活动:
例:若点p在第四象限,且点p到x轴、y轴的距离分别为4,3.则点p的坐标为( )。分析:(1)想象出第四象限为(+、-)。(2)距离都为正。(3)点p到x轴距离为4,即纵坐标为-4,点p到y轴距离为3,即横坐标为+3.所以p(3、-4)。
这样的教学活动不仅让学生认识平面直角坐标系中的计算方法,更深刻地理解了点在平面直角坐标系中的关系。当然,在课堂教学活动中,没有固定的培养学生数学思维能力的模式。应该综合分析学生的年龄特征、知识水平和学习内容等现实情况再做选择和调控,而不是按照设计的教学计划进行机械操作。教师应始终关注学生的思维状态,根据师生互动中的反馈信息,自如地掌握学习过程,并调整学习方法。通过老师和学生的配合,学生既可以获得知识,也可以获得数学思维能力的发展。
3.设计灵活作业练习,巩固学生数学思维
作业练习的目的是进一步增强学生的思维能力,但学生通过有组织、分层、集约化的课堂学习感到疲倦,所以在设计作业时,我们是这样做的:注意缓解学生思维的紧张。用合作练习代替学生冥想,实现多样化的、灵活的、适用的、有趣的解决问题环境。这不仅可以帮助学生巩固知识,提高解决问题的能力,而且可以训练学生的数学思维,培养学生的智力。作业设计应具有针对性、层次性、综合性和创造性,将教学内容与学生结合起来。在实践中,对不同水平的学生要分层安排作业,实现“相同起点,不同终点,分层次达标”的目标。
二、启发学生数学思维,引导学生寻找规律
“学而不思则罔,思而不学则殆”,学与思是学习过程中缺一不可的法宝,要让学生学习基础数学知识、基本数学技能,也要让学生总结必要的基本分析方法,使学生的思维活跃在数学学习中,培养学生正确的数学思维方式,教师应该坚持启发式教学,培养学生的思维能力。
數学教育是对学生思考的启发。在授课过程中,教师应当指导学生遵守、发现、总结和掌握规律。这是一种有效的学习方法,它克服了干扰,提高了学生的认知能力,使思考水平的发展成为一个新的高度。概念和规则的形成过程是教育的重要环节,学生在这个过程中不仅要知道做什么,还要知道为什么这么做。该形成过程既可以由教师指导学生进行,也可以教师自己完成整个形成过程。
在数学的解决过程中,我们要多加注意。解决问题的重点是学习发掘隐藏环境的能力和如何解决问题的能力。分析可从条件到结论或从结论到条件。关于数学上的问题,首先必须确定问题的范围,必须确定哪个概念、规则或者计算式参与其中。在解决问题的过程中,学习运用数学符号。这样思维才会得到训练,思维能力才会得到提高。
培养学生的思维能力有多种方式,其中最根本的是调动学生学习数学的积极性,教师要善于启发、引导、鼓励学生,及时解决学生的疑问,答疑解惑。学而不思、思而不学都不能达到学习目的,教师要让学生把学习转变为思考。当然,良好的数学思维品质不是一朝一夕形成的,但通过老师和学生的共同努力,在科学的教学方案下,持之以恒,一定会达到预期的目标。
编辑 郭小琴

