基于Herschel-Bulkley模型的磁流变阻尼器转矩模型参数辨识*

欧阳青,胡红生,宋玉来,郑佳佳,王 炅

(1.嘉兴学院机电工程学院,浙江 嘉兴 314033;2.浙江师范大学工学院,浙江 金华 321004; 3.南京理工大学机械工程学院,南京 210094)

旋转式磁流变阻尼器可弥补直线式磁流变阻尼器[1-2]无法直接应用于旋转工况的不足,并具有结构紧凑、降低扭转振动、传递转矩的能力等,目前已开发出相应的试验样机,如磁流变离合器[3-4]、联轴器[5]、扭振器[6]等,具有广泛应用前景。

针对旋转式磁流变阻尼器的动力学模型大多是基于Bingham模型建立的,虽因结构简单且能较好反映阻尼力-位移的关系而在器件初期设计阶段及性能考察时广泛应用[7-9],但模型未考虑液体在高剪切速率下的剪切稀化现象,会高估输出扭矩值。而Herschel-Bulkley模型能反映磁流变液的剪切稀化现象,尤其适用于描述高旋转速度工况下的磁流变器件力学特性[10-12]。由于Herschel-Bulkley模型具有两个与磁场强度相关的液体流动行为指数k和n,使得模型在不同磁场情况下没有统一表达式[13],大多通过数值计算方法进行Herschel-Bulkley模型分析,而难以将该模型嵌入至有限元仿真中进行力学特性分析工作。

论文针对多级线圈的旋转式磁流变阻尼器,旨在通过全局优化方法对基于Herschel-Bulkley的力学模型进行参数辨识,获得了该模型在各磁场条件下的最佳模型参数k和n,解决模型参数磁场相关性所引起的模型表达式不统一的问题,为后续建立基于Herschel-Bulkley模型的有限元仿真模型的建立提供理论依据。

1 多级旋转式磁流变阻尼器结构

图1 多级旋转式磁流变阻尼器结构图及实物图

多级圆筒式磁流变阻尼器结构如图1所示,主要包括主动输入轴、从动输出套筒以及填充于两相对旋转部件之间的磁流变液等。四级并联线圈分别绕在环形线圈骨架上并沿轴向逐一嵌于套筒内,各级线圈可根据具体应用需求进行加载电流,实现不同工作线圈模式下输出转矩范围的可调。磁力线经环形导磁部件、主动输入轴,沿径向均匀通过液体通道形成回路。

主动输入轴与从动套筒之间通过磁流变液来传递转动力矩,其中主动输入轴与驱动设备相连接,而从动套筒则与负载相连。为保证输入轴在旋转工作时的稳定性,轴两端通过定位轴承与从动套筒实现定位。同时,在轴承端面覆有密封盖板,并在端面与密封盖板之间注入锂基润滑脂以避免磁流变液中的铁磁颗粒进入轴承内部,影响轴承的工作流畅性。

2 圆筒式磁流变联轴器力学模型

2.1 Herschel-Bulkley本构模型

采用Herschel-Bulkley 本构模型来描述液体屈服后的剪切稀化现象,其本构关系可表达为[14]:

图2 Herschel-Bulkley本构模型

2.2 转矩传递力学模型

图3 旋转式磁流变阻尼器流体剪切区示意图

2.2.1 库伦扭转剪切区力学模型

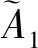
(3)

式中,Lp为流体区域的轴向长度。

环形通道中液体的剪切应力可简化为通道内外表面应力的算术平均值[17]:

(4)

则液体的本构力学模型可表示为:

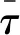
(5)

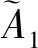
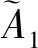
(7)

2.2.2 粘性扭转剪切区力学模型

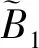
式中,R0和R2分别为该区域流体内外壁的半径。

则该区域流体的剪切应变率为:

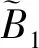
(10)

由式(7)和式(12)可以得到圆筒旋转式磁流变阻尼器的总扭矩为:

(13)

式(13)等号右侧第一项为流体因磁流变效应而产生的库仑扭矩项,第二项为流体通道的粘性扭矩项。

2.3 库伦剪切区屈服应力

所设计的阻尼器采用美国Lord公司提供的MRF-132DG型磁流变液,其力学性能与磁化特性可用以下方程拟合,建立磁流变液剪切屈服应力与磁感应强度的关系:

τy=4.141×10-7H3-7.842×10-4H2+0.351H-0.704

(14)

B=1.321×10-8H3-1.555×10-5H2+7.27×10-3H+

1.188×10-1

(15)

式中,H和B分别为磁场强度和磁感应强度。

通过COMSOL Multiphysics有限元分析软件获得不同输入电流与磁感应强度的对应关系,结合上面式(14)、式(15)得到各库伦扭转剪切区域中液体的剪切屈服应力与输入电流的对应关系,如图4所示。

图4 库伦扭转剪切区屈服应力和电流关系

3 力学性能试验

式(13)所建立的理论转矩模型需通过实验数据拟合,确定磁流变液的流动行为参数k和n。其中总扭矩T可由扭矩传感器测得;主动输入轴转速Ω为试验条件参数,由伺服电机输入转速决定;τyAj则根据图4获得;R0、R1、R2、Lp以及Le等为已知的几何参量。

3.1 测试系统

搭建的旋转式磁流变阻尼器扭转力学特性测试平台如图5所示,由交流伺服电机(MS0040A)作为扭转动力源,并经联轴器将扭转动力传递到旋转式磁流变阻尼器中,带动阻尼器输入轴转动。而磁流变阻尼器的从动套筒则与扭矩传感器(RTS-1K型)相连,一并固连于台架基座之上。传感器所采集到的数据通过双通道数据记录仪(INSTRUSTAR ISDS205A型)进行采集及分析。

图5 阻尼器力学性能测试系统

3.2 试验结果

测试了不同电流下,转速从零线性增至1 000 r/min时磁流变阻尼器的输出扭矩的变化值,由图6可知,磁流变阻尼器的输出扭矩与线圈输入电流呈正相关,电流越大则磁流变阻尼器所提供的库伦扭转剪切力也越大,从而使输出总扭矩增大。在相同电流情况下,输出扭矩随转轴转速的变化波动较大,尤其是在测试初始阶段的低转速情况下,直至转速增至200 r/min左右时,扭矩逐渐呈平稳状态。

磁流变阻尼器的输出扭矩值随通电线圈电流(即液体屈服应力)和转速的增大而大致呈上升趋势,这三者关系如图7所示。通过图7的三维散点图可知,当输入电流较小、转速较低时,所测得的扭矩值变化较大,扭矩结果的分布也较为分散,这在一定程度上说明测试初期阶段的扭矩结果的不稳定性。当电流、转速逐渐增加时,磁流变装置运行趋于稳定,扭矩值的波动性相对较小,结果散布也较为集中。扭矩的整体变化趋势与电流、转速呈正相关变化规律。

运用1stOpt优化分析软件的Levenberg-Marquardt算法和通用全局优化算法,对实验所涉及的流体屈服应力、转轴转速以及输出扭矩值这三者参量进行多参数非线性回归分析,得到最佳的流体参数值:k=49.88;n=0.576。即通过对式(13)的参数辨识,获得精确的磁流变阻尼器的扭转力学模型。在不同试验条件下,磁流变阻尼器扭矩的整体拟合效果如图8所示,拟合后得到的扭矩曲线的整体变化趋势与实测扭矩值的分布趋势基本一致,拟合均方差为0.102,不同电流(或屈服应力)情况下的扭矩曲线分段变化。

由以上分析可知,通过多参数非线性回归分析可以在全局范围内建立形式统一的基于Herschel-Bulkley的扭转力学模型,确定形式的力学模型为磁流变阻尼器的动力性能预测提供理论基础。

图6 不同加载电流时的实测扭矩随转速的变化规律

图7 流体屈服应力、转速以及实测扭矩的三维散点图

图8 拟合扭矩的整体趋势与实际扭矩点的对比图

4 结论

①针对多级线圈形式的旋转式磁流变阻尼器,分别建立库伦扭转剪切区和粘性扭转剪切区的转矩力学模型,并通过各子区域转矩之和获得阻尼器的总输出扭矩。

②基于Herschel-Bulkley模型建立了旋转型磁流变阻尼器的转矩力学模型,通过Levenberg-Marquardt算法和通用全局优化算法对力学模型进行参数辨识,获得了该模型在各试验条件下的最佳模型参数k和n。所建立的统一形式的Herschel-Bulkley动力学模型可为后续的器件性能有限元仿真及动力学分析提供理论支撑。

③试验过程中存在输出扭矩波动较大的现象,尤其是在测试初期阶段扭矩值相对偏大,这可能与阻尼器转子在启动阶段的静摩擦力较大有关,论文所设计的器件虽然在轴承端面覆有密封盖板以避免磁流变液体进入轴承内部,但是密封结构仍然存在缺陷。在之后设计中应尽可能保证器件顺畅性,减少部件之间的摩擦力。