基于七元传声器阵列的声源定位算法及性能分析*
杨 旭,行鸿彦*,张 军,冯茂岩
(1.南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044; 2.南京信息工程大学江苏省气象探测与信息处理重点实验室,南京 210044; 3.江苏海事职业技术学院,南京 211170)
随着社会现代化的日益发展,声源定位已然成为新的研究热点。利用外界的声源信号,人类可以收集环境中的重要信息。声源定位实际上就是先通过某一设备接收声源信号,然后对接收到的信号进行处理,从而确定目标声源具体位置[1]。声源定位技术主要分为主动声和被动声定位[2]。相比于主动声定位,被动声定位具有较强的隐蔽性和抗干扰性。现有声源定位手段难以快速而准确地对声源进行定位,因此,为了更好地获取目标声源的位置信息,应首先对传声器阵列[3-4]和声源定位算法[5-7]进行改进。
在国外,声源定位技术主要应用于语音信号处理[8]和军事领域[9]。比如,英国的Ferranti公司装备的Picker直升机报警系统和美国的ERAM远程反装甲智能地雷[10]等,均具备多目标探测和识别能力,具有较高的系统性能。基于匹配或不匹配的分析窗口,文献[11]进行了AMS处理期间的幅度和相位谱估计,采用最小均方误差(MMSE)短时频谱幅度(STSA)估计来代替噪声幅度谱,通过准确的相位谱估计改进了语音质量。文献[12]提出了一种多面离散的球形麦克风阵列,与几何形状稍有不同的球形麦克风阵列进行了比较,获得了高精度的声源定位数据。文献[13]利用300个传声器搭建了传声器阵列,通过深入研究,在对于多声源定位问题上有很大突破。
虽然我国在声源定位技术领域的研究落后于一些先进国家,但在国家高技术研究发展计划(863计划)资助下,我国一些机构相继展开了对目标声源探测的研究。文献[14]提出了一种强气流背景噪声下的声源定位方法,解决气动测试中声源定位的强背景噪声干扰问题。通过集合经验模态分解将气流背景噪声信号和待分析源信号自适应地分解到不同分量中,再利用波束形成算法,获得声源定位云图。文献[15]结合远场窄带信号的子阵算法和麦克风阵列信号处理的特点,把阵列分成两个位置不同的子阵,利用两个子阵的互相关矩阵,实现声源定位。文献[16]将声源所处的三维空间位置划分为四种情况进行研究,提出一种声源方位定位算法,有效解决声源定位产生计算盲区问题。然而,现有算法仍存在计算量大、精度低等问题。
本文结合方位估计算法,研究基于七元传声器阵列的声源定位算法。建立七元传声器阵列模型,得出声源方位计算公式。利用传声器阵列参数与定位性能的关系,对测距测向精度进行分析。在正演数据基础上,对声源方位进行反演,说明算法具有较高的精度和稳定性。
1 七元传声器阵列模型
建立如图1所示的七元传声器阵列模型。
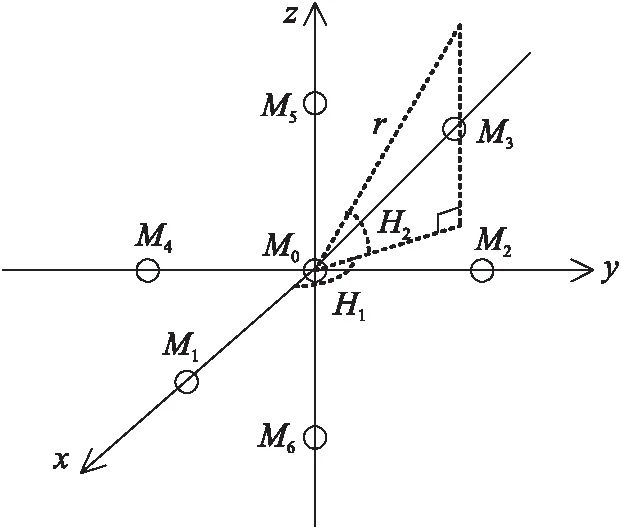
图1 七元传声器阵列模型
图1中,声源S的空间位置为(x,y,z),r为声源到阵列中心M0的距离。传声器阵列阵元间距为a,声源传播到传声器M0(0,0,0)、M1(a,0,0)、M2(0,a,0)、M3(-a,0,0)、M4(0,-a,0)、M5(0,0,a)、M6(0,0,-a)的时间分别为t0、t1、t2、t3、t4、t5、t6,并根据模型设定5组相对时延值:T1=t1-t0,T2=t2-t0,T3=t3-t0,T4=t4-t0,T5=t6-t5。H1、H2分别为声源的水平偏角和仰角,另设声音传播速度为c。
2 七元传声器阵列声源定位算法
基于图1,表示出声源S到传声器M0、M1、M2、M3、M4的距离:
根据式(1),得出:
根据式(2),得出:
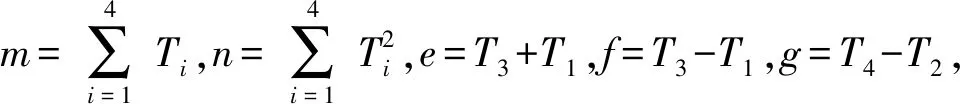
式中,x′,y′分别为声源坐标参数正演值x,y的反演值。
再次利用式(1),得到:
式中,r′为声源到坐标原点距离r的反演值。
根据图1所示阵元间矢量关系,得出:
式中,z′为声源坐标参数正演值z的反演值,H′1、H′2分别为声源水平偏角H1和仰角H2的反演值。
利用式(6),得到:
利用式(7),可得到声源仰角H′2的值。再次利用式(6),可求出z′,实现声源定位。
3 基于七元传声器阵列的声源定位算法性能分析
根据间接测量误差理论[2],研究声源定位算法性能,对其测距测向误差进行分析。假设各时延估计误差的标准差均为στ,且相互独立。
3.1 声源定位水平偏角估计误差分析
由时延估计误差στ引起的声源水平偏角H1的估计误差σH1τ为:
取时延估计误差στ为1 μs,对式(8)进行仿真,结果如图2所示。
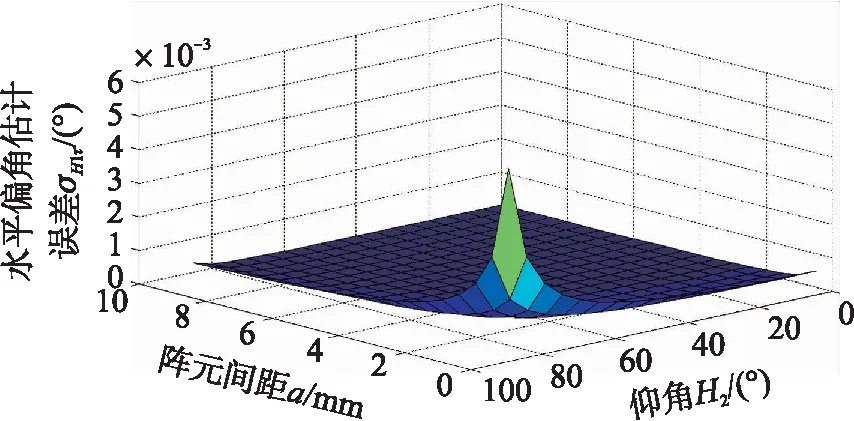
图2 水平偏角估计误差与仰角、阵元间距的关系曲线
图2中,水平偏角估计误差σH1τ与水平偏角H1无关,但受时延估计误差στ、阵元间距a及仰角H2的影响。阵元间距a增加,估计误差σH1τ随之减小;误差σH1τ随着仰角H2的减小而减小。因此,相对于高空声源定位,这种情况对低空和地面声源的定位更加准确。
当阵元间距a为2 m,仰角H2分别为15°、30°、45°、60°时,水平偏角H1的估计误差σH1τ与时延估计误差στ的关系曲线如图3所示。
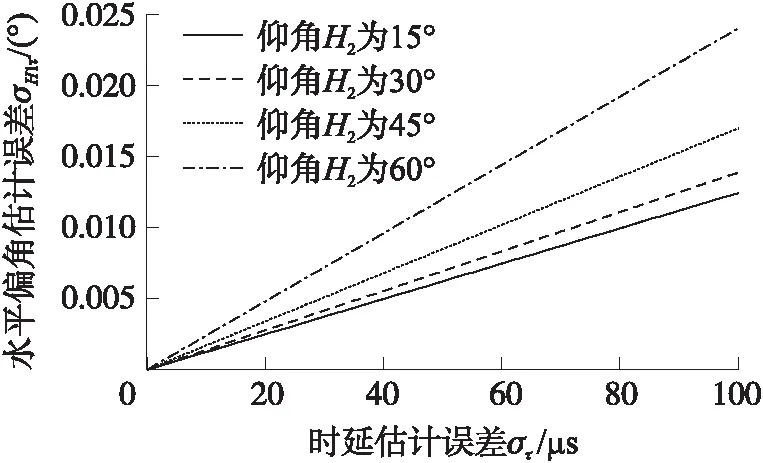
图3 水平偏角估计误差与时延估计误差的关系曲线
由图3可知,当声源仰角H2的值一定时,水平偏角H1的估计误差σH1τ随着时延估计误差στ的增加而线性增大;随着仰角H2的增大,水平偏角估计误差σH1τ与时延估计误差στ的线性变化愈加剧烈,这表明,时延估计误差στ对水平偏角估计误差σH1τ有较大影响,误差στ的增加会导致水平偏角估计精度骤降,误差σH1τ最大达到0.024°。
3.2 声源定位仰角估计误差分析
由时延估计误差στ引起的声源仰角H2的估计误差σH2τ为:
取时延估计误差στ为1 μs,对式(9)进行仿真,结果如图4所示。
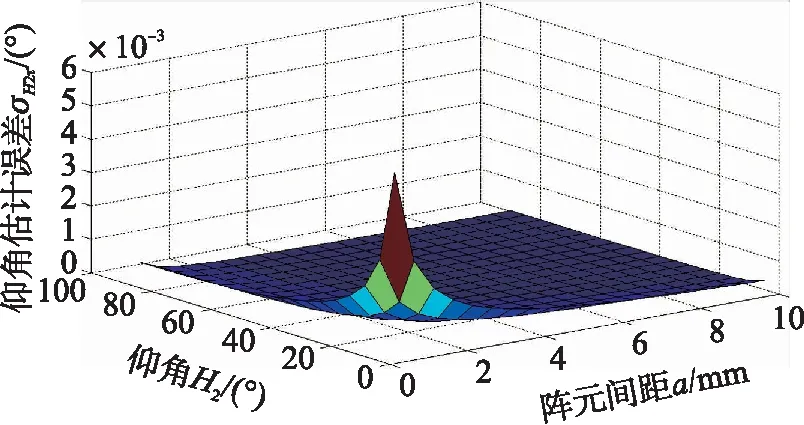
图4 仰角估计误差与仰角、阵元间距的关系曲线
由图4可知,仰角估计误差σH2τ与水平偏角H1的值无关,但同样会受时延估计误差στ、阵元间距a及仰角H2的影响。仰角H2的估计误差σH2τ随着阵元间距a的增加而减小;仰角H2自身值的变化会引起其估计误差σH2τ的变化,且随着仰角H2的增大,误差σH2τ会随之减小,即仰角测量精度会增加。
当阵元间距a为2 m,仰角H2分别为15°、30°、45°、60°时,仰角H2的估计误差σH2τ与时延估计误差στ的关系曲线如图5所示。
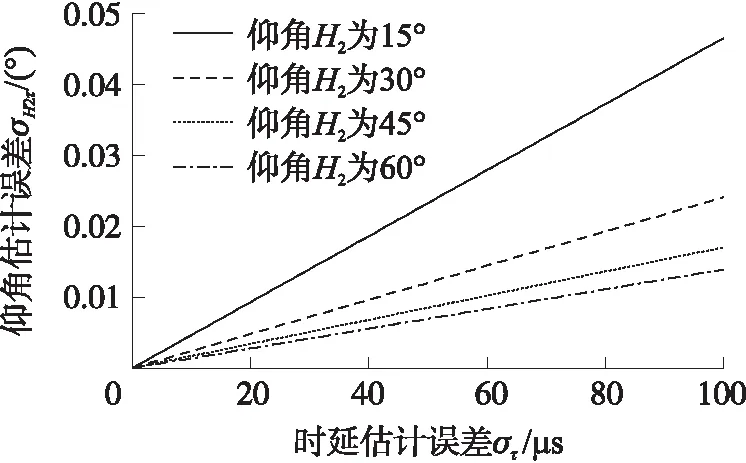
图5 仰角估计误差与时延估计误差的关系曲线
图5中,当声源仰角H2的值一定时,其自身估计误差σH2τ随时延估计误差στ的增加而线性增加;随着仰角H2的减小,仰角估计误差σH2τ与时延估计误差στ的线性变化愈发剧烈,这表明,时延估计误差στ对仰角估计误差σH2τ有较大影响,误差στ的增加会导致仰角估计精度骤降,误差σH2τ最大达到0.046°。
3.3 声源到阵列中心距离估计误差分析
声源S到阵列中心M0的距离r的估计误差σrτ为:
(10)
取声源仰角H2为45°,时延估计误差στ为1 μs,对式(10)进行仿真,结果如图6所示。
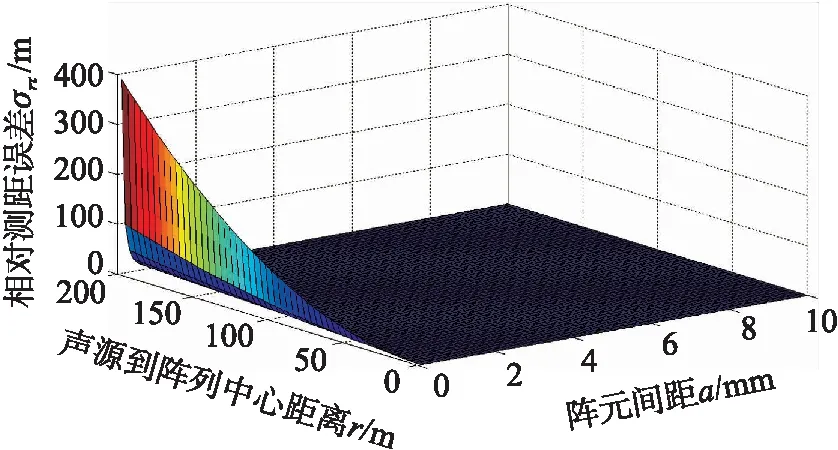
图6 相对测距误差与声源到阵列中心距离、 阵元间距的关系曲线
由图6可知,当时延估计误差στ和阵元间距a一定时,声源到阵列中心距离r的增大,会使相对测距误差σrτ增大,即相对测距性能下降。相对测距误差σrτ随着间距a的增加而减小,测距精度有所提高。同时,间距a不宜小于2 m,否则,测距误差σrτ较大,会对声源定位性能产生较大影响。
当仰角H2分别为30°和60°,相对测距误差σrτ分别为0.05 m和0.10 m,声源到阵列中心距离r为100 m时,时延估计误差στ与阵元间距a的关系如图7所示。
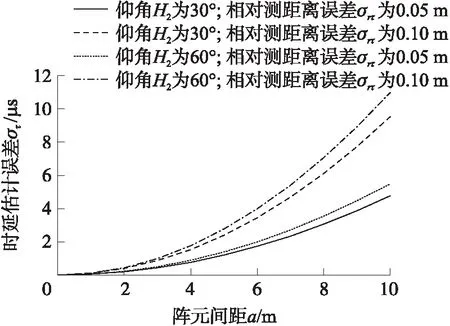
图7 时延估计误差与阵元间距的关系曲线
根据图7,当传声器阵元间距a一定时,相对测距误差σrτ比仰角H2对时延估计误差στ的影响大;当测距误差σrτ和仰角H2的值均较大时,阵元间距a的增大给时延估计误差στ带来指数性增长。特别地,当阵元间距大于8 m后,误差στ的增加更为显著,因此,建议间距a不宜设定过大。
当仰角H2分别为30°和60°,相对测距误差σrτ分别为0.05 m和0.10 m,阵列尺寸a为2 m,声源到阵列中心距离r变化时,时延估计误差στ与声源到阵列中心距离r的关系如图8所示。
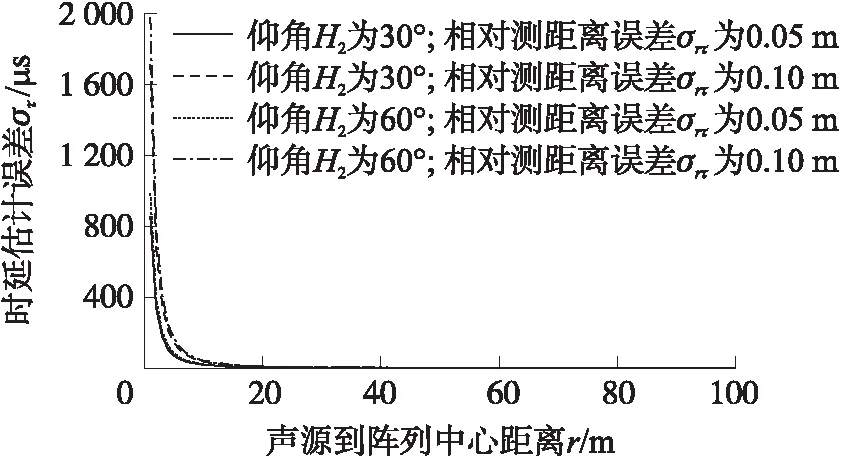
图8 时延估计误差与声源到阵列中心距离的关系曲线
从图8看出,当声源到阵列中心距离r较大时,时延估计误差στ几乎为零;而距离r与误差στ的曲线在r较小时变化剧烈,特别地,当声源距阵列中心非常近时,时延估计误差στ趋于无穷大,这表明,不宜对离阵列中心太近的声源进行定位。
4 实验结果与分析
在实际测试的过程中,利用声传感器构建七元传声器阵列声源定位数据采集系统,在Keil5软件平台编写程序,利用Flymcu接收串口的发送数据,测量出5组相对时延值,利用时延值计算出声源所在方位。室内测试地点选于南京市浦口区南京信息工程大学电子与信息工程学院实验室,利用便携式蓝牙音响作为声源。调整阵元间距a为0.5 m,搭建如图9所示的七元传声器阵列,将声源定位算法引入到阵列中,在已测得坐标的两个位置(60,-20,100),(-30,0,-90)(单位:m)处进行实验,对声源方位进行反演,得到如表1、表2所示结果。将本实验数据与文献[16]中2018年1月12日的实测数据进行对比,结果如表3所示。

图9 七元传声器阵列声源定位数据采集系统
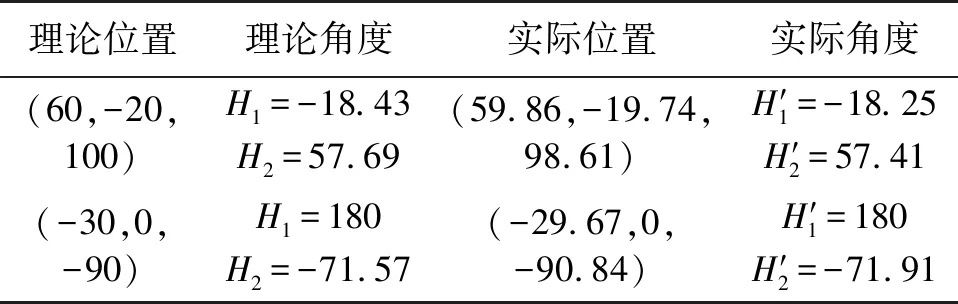
理论位置理论角度实际位置实际角度(60,-20,100)H1=-18.43H2=57.69(59.86,-19.74,98.61)H′1=-18.25H′2=57.41(-30,0,-90)H1=180H2=-71.57(-29.67,0,-90.84)H′1=180H′2=-71.91

表2 声源定位算法误差率

表3 与文献[16]对比结果
图9中,本实验使用了一种具有良好全向性的压力传声器,其接收信号的带宽为12 kHz。并且,在Keil5.map文件中,本算法的代码加数据所占单片机内部flash大小为5.88 kbyte。
表1中,声源定位算法反演数据与理论数据相接近,结合声源坐标参数的正负性可知,该算法具有较高的定位精度和稳定性,能够实现空间声源的全方位定位。
表2中,根据声源定位算法的误差率可知,声源位置误差率在1.0%左右,方位角误差率在0.5%左右,虽然有一定偏差,但是仍然在可接受范围之内,所得数据较为可靠。
表3中,文献[16]提出了一种基于四元传感器阵列的声源全方位定位算法,其位置、水平偏角和仰角的最大误差率分别为5.70%,5.70%,2.06%,而本文算法在这三个方面的误差均下降至1.10%,0.98%,0.49%,表现出了较好的声源定位精度。另外,由于文献[16]的声源方位估计公式是从方位角式(10)得到的,这增大了误差传递的可能性,虽然通过适当增大阵元间距减小了定位误差,但对实际定位性能仍造成了负面影响。而本文基于声源定位基础式(1),直接推导出方位估计式(4)和式(5),这不仅减少了运算复杂度,而且有效减小了误差传递性,能够确保声源定位算法定位性能的稳定性。
综上所述,在测量实验中,基于七元传声器阵列的声源定位算法的测量效果与理论结果接近。通过实验显示了算法精度和稳定性较好的优势,能够得到预期的定位效果。
5 结论
基于传声器阵列模型,将方位估计算法引入到阵列模型中,本文提出了基于七元传声器阵列的声源定位算法。对算法性能进行分析,在正演数据基础上进行声源方位反演,结果表明该算法有着较好的精确性,能够很好的得到声源方位数据。
七元传声器阵列在平面上使用对称四棱锥形作为七个传声器的排列结构,可调控传声器间阵元间距,以降低传声器布置区域密集程度。结合声源定位算法性能分析可知,适当增大阵元间距,还可提高声源定位精度。
基于传声器阵列声源定位算法精度有很大提升空间,在实际环境中涉及的问题还很多,假设的模型也比较理想。如何将室内实验转移到野外进行性能测试,减小实际环境中声源定位误差等方面,都需要在接下来的工作中做进一步的探索和研究。

