一种面向图像分类的流形学习降维算法

刘开南 冯新扬 邵 超

1(三亚学院信息与智能工程学院 海南 三亚 572022)2 (河南财经政法大学计算机与信息工程学院 河南 郑州 450000)

0 引 言

在人工智能与数据挖掘问题中，最常见的是高维数据的提取与分析。近年来提出的高维数据降维算法和特征提取算法，它们在模式识别、图像分类中已取得了较好的结果[1-3]，这些算法关注于寻找原始数据集特征表示中有价值的信息，在图像分类技术中得到了广泛应用。

降维算法的目的是为了揭示出在高维数据空间中样本数据的固有的组成特性[4-6]。传统的线性降维算法有主成分分析法(principal component analysis,PCA)、线性判别分析法(linear discriminant analysis,LDA)、多维尺度分析法(multi-dimensional scaling,MDS)等。基于流形学习的降维方法有核函数主成分分析法(kernel PCA[7])、局部线性嵌入分析法(locally linear embedding,LLE)[8]、黑塞局部线性嵌入方法[9]、ISOMAP分析法、拉普拉斯特征映射(Laplacian Eigenmaps,LE)，局部保持投影分析法(locality preserving projections,LPP)和局部切空间对齐分析法(local tangent space alignment,LTSA)。这些算法都可以针对样本数据在高维数据空间完成降维[10-12]。但是同时它们也会破坏原始数据固有的组成结构，而且当高维数据空间中数据点处于非均匀性状态时，会导致降维后数据的嵌入结果比较差。

为了解决这个问题，本文提出了一种面向图像分类的新型流形学习算法，它是针对局部线性嵌入算法的改进，称为Mod-LLE。Mod-LLE算法整合了识别信息来更好地改善优化效果，这样就可以保证高维原始数据固有的拓扑组成结构信息。把Mod-LLE算法应用到数据挖掘的图像分类领域，通过实验证明，Mod-LLE方法与LLE降维算法比较起来，可以获得比较好的图像分类效果和降维效果。

1 算法描述

本节主要描述高维数据降维算法Mod-LLE，它主要针对图像的分类这个数据挖掘类应用。把高维图像样本数据映射到低维图像数据的过程中，Mod-LLE算法整合了图像数据的识别信息，这样就可以保证原始数据的相互组成关系信息。整体来说，Mod-LLE算法通过寻求高维数据固有的拓扑结构来更好地发现数据之间隐藏的关系，同时寻找具有代表性的维度信息。

1.1 LLE分类算法描述及缺陷

原始LLE降维算法中，假设X={x1,x2,…,xN}是在RD空间中N个样本的数据集，这里xi∈RD(i=1,2,…,N),D是数据集的维度。

在每个数据点xi处，使用xi所选择的k个邻居来表示局部线性组成情况。优化权重是通过下面的优化方法来完成的：

通过权重矩阵W={wi=(wi1,wi2,…,wiN)}T来完成重构，LLE算法把X={x1,x2,…,xN}映射到Y={y1,y2,…,yN}，这里Y是一个低维数据空间，根据下式，Y中保持了高维数据的局部固有属性。

(2)

s.t.YYT=I

这里I是一个具有N×N的单位矩阵，LLE算法通过这些过程完成优化，它可以获得d个特征向量，这样就可以把Y构造到一个低维数据空间。当高维空间中样本数据是均匀的时候，LLE算法被认为是一个好的降维算法;但是当高维空间中样本数据是非均匀的时候，LLE算法破坏了原始数据的局部固有拓扑组成，会导致一个比较坏的低维嵌入结果。图1显示了这种情况,把3维数据空间降到2维数据空间，可以看到LLE算法完全改变了原始局部数据固有拓扑结构组成。

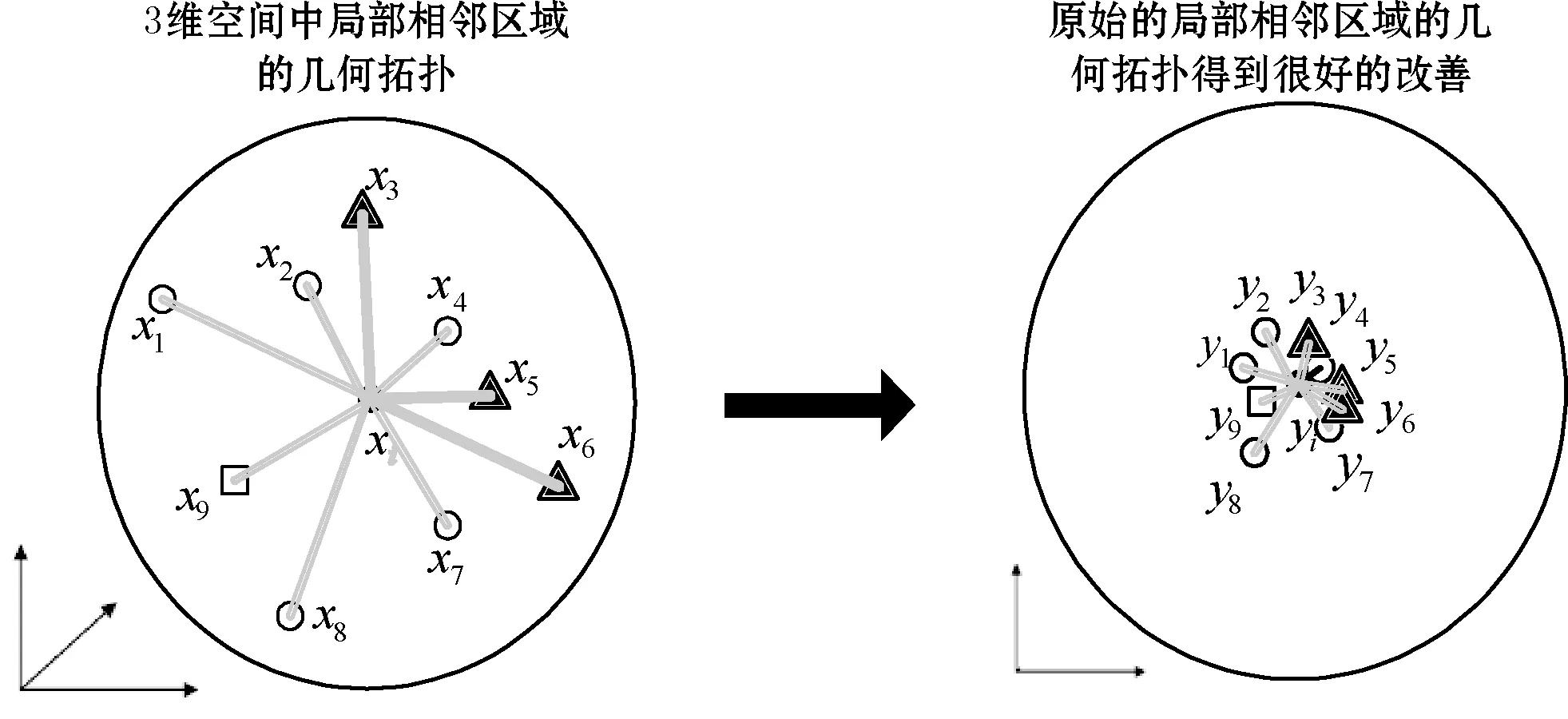
图1 利用LLE算法将3D降维到2D数据局部嵌入结果

1.2 改进分类算法描述

LLE算法使用重新构造权重{wij}来保证原始数据的固有拓扑组成，但是对于每个xi, LLE算法不能反映出与信息最相近的k个邻居密度信息。

为了克服这个缺陷， Mod-LLE算法可以保证原始数据的本身固有的拓扑组成结构。在Mod-LLE中，使用识别信息来更好地提取高维数据内部类的距离信息。这样做的目的是在映射一个非均匀分布的高维数据避免一起带入了不同类的样本点。如图2所示。

图2 Mod-LLE算法的局部相邻区域的优化结果

这里设计的目标函数使用下面的公式来描述：

s.t.YYT=I

式中：α和β是两个比例因子，用来统一与调整不同的权重所占的比例，α+β=1。

Mod-LLE针对高维图像分类降维方法可以用下面的流程来表示。

输入:D维数据空间中N个样本中的X个数据集；

步骤1：对每个xi，寻找k个最接近邻居;

步骤2：根据式 (1)计算局部重构权重{wij};

步骤3： 在Rd低维数据空间中映射数据集X→Y；

步骤4：通过优化式(3)的目标函数来对Y进行优化，得到最后的结果；

输出: 降维嵌入后的结果Y。

2 实验与性能分析

2.1 图像分类效果分析

为了测试Mod-LLE算法的性能，选择脸部图像分类为示例，这些数据来自于FFace数据集[8]。为了测试算法在面对非均匀分布数据的效果，随机选择了300幅人脸作为样本，这些都是有高维空间的观察数据。根据图像面部表情，利用Mod-LLE把这些数据集分到5个不同的类别中：正常脸部表情(neutral)；高兴脸部表情(happiness); 生气脸部表情(anger); 吐舌脸部表情(tongued); 撅嘴脸部表情(pouty)。

表1显示了LLE方法和Mod-LLE的识别精度。其中，图3(a)和(b)显示了FFace 数据集中这些图像Mod-LLE方法和LLE方法分类到2维空间后的效果，在最接近邻居个数k=6的情况下LLE和 Mod-LLE算法完成了性能比较。从表1和图3可以清楚地看出，Mod-LLE算法可以在2维数据空间中清楚地分离出高兴脸部表情、生气脸部表情和正常脸部表情，精度都达到90%以上，人脸图片分类效果明显优于LLE算法。

(a)

(b)图3 局部线性嵌入LLE算法分类效果

%

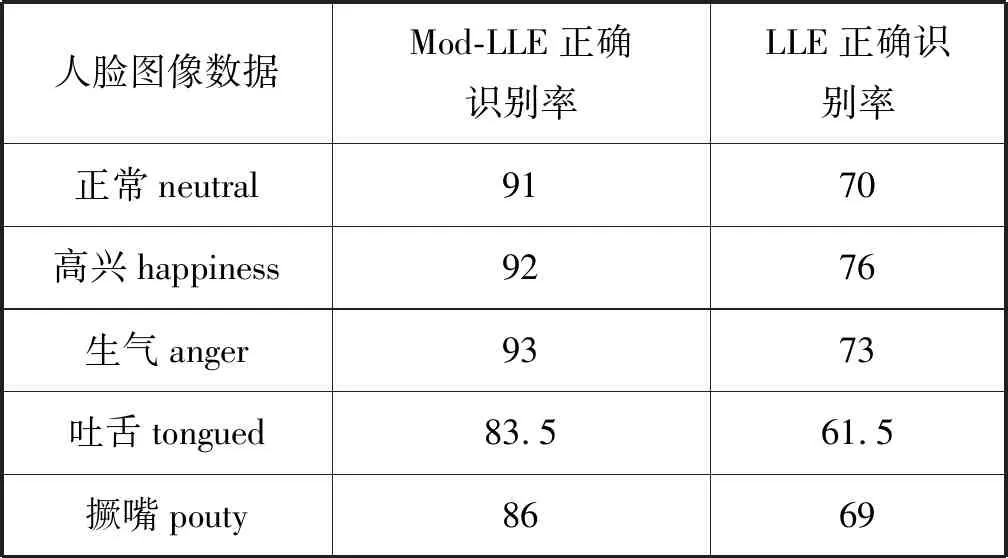
2.2 降维效果分析

这个部分主要测试Mod-LLE算法的降维性。测试的数据集来自于图4所示R3空间的人工智能S-curve数据集。图5显示的是S-curve数据集的散点图。可以看出，S-curve的数据由2 000个高维、非线性、流形随机产生的点组成。在最接近邻居个数k=16的情况下，把S-curve数据集从3维空间嵌入到2维流形空间中。Mod-LLE 和 LLE的计算结果如图6和图7所示。

值得注意的是，k是每个样本点xi被选择的最接近邻居个数，从图7中可以清楚的看到，Mod-LLE算法可以很好地保持S-curve数据集固有的拓扑组成情况。LLE算法正好相反，图6显示它对S-curve数据集的固有的拓扑组成情况进行了很大改变，没有保持多维数据的一致性。分析原因是Mod-LLE算法在重新构造权重矩阵时{wij}可以保证原始数据的固有拓扑组成。而且式(3)是线性无关，具有最优近似解，α和β是两个比例因子，它们和最接近邻居个数k都很好进行调整，使Mod-LLE有很好的降维效果。

图4 S-curve 数据集

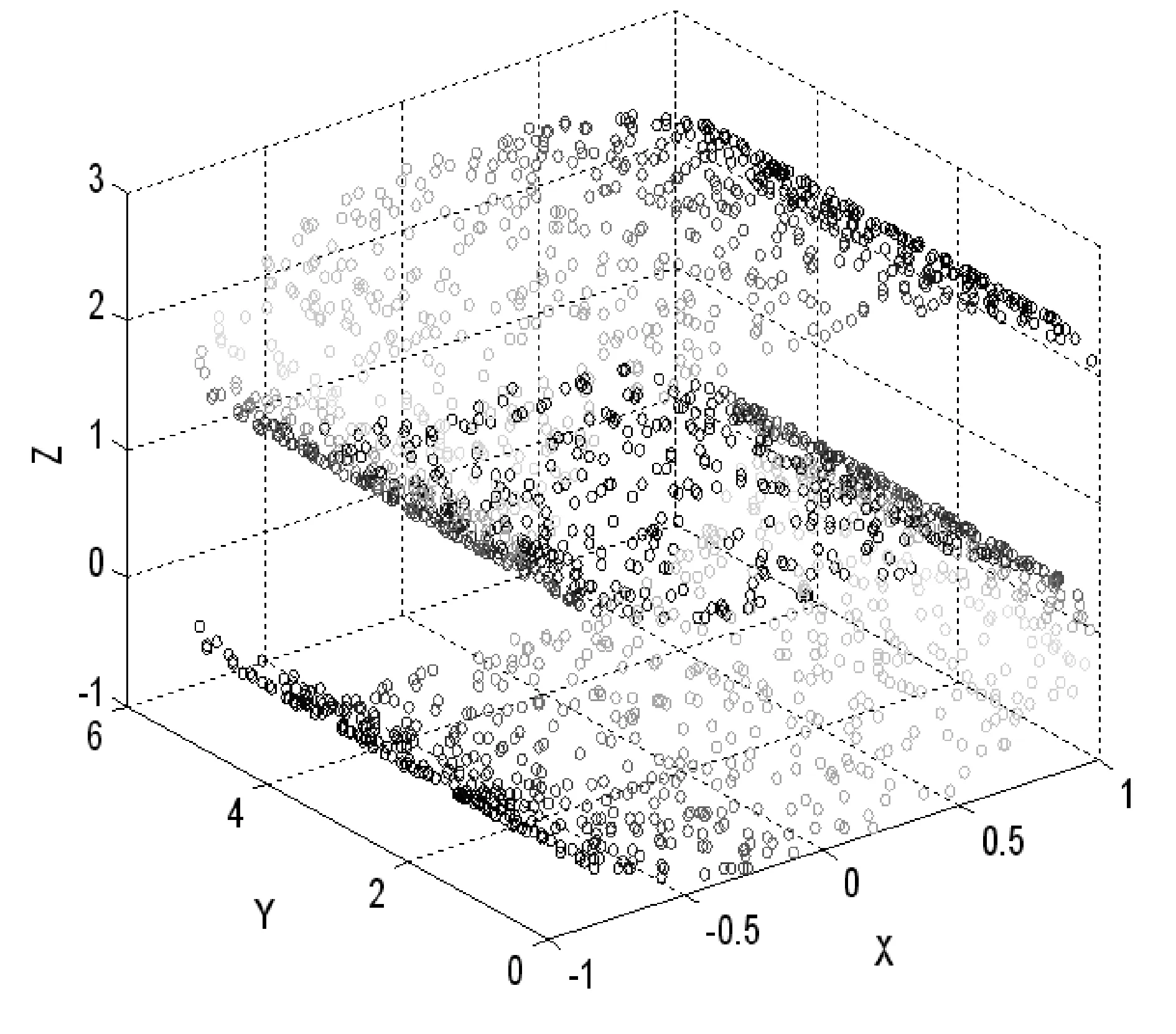
图5 S-curve 数据集在N=2 000情况下样本点散点图

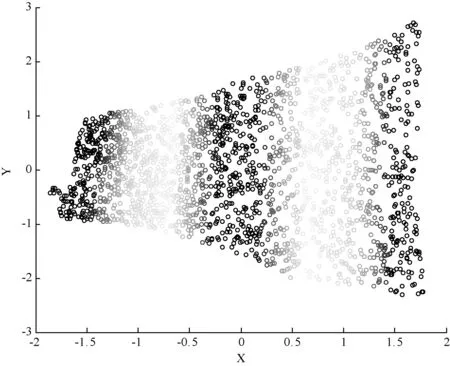
图6 LLE针对S-curve 数据集的2维嵌入效果

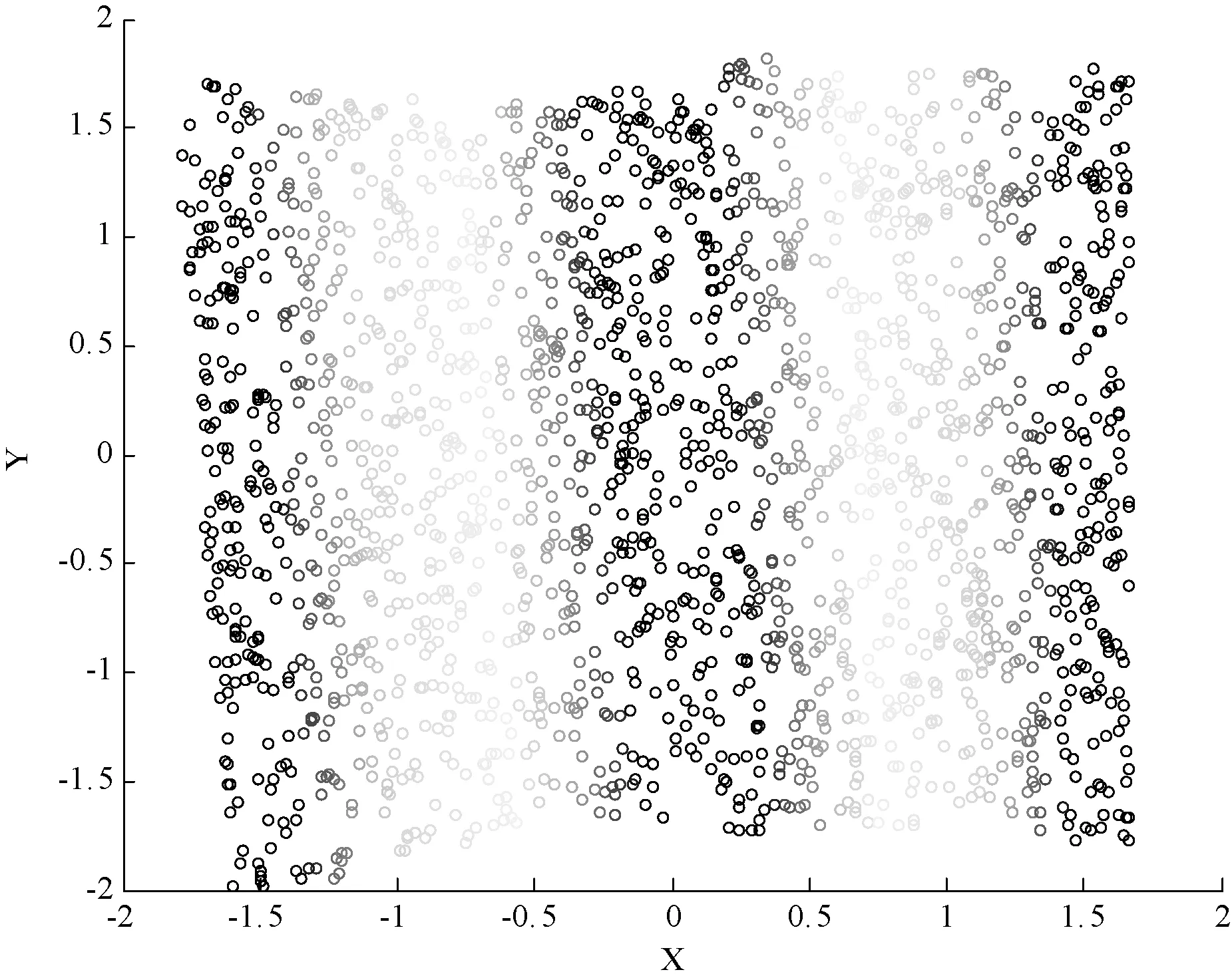
图7 Mod-LLE针对S-curve 数据集的2维嵌入效果

3 结 语

本文提出了一个面向图像分类的流形学习降维算法Mod-LLE，它基于局部邻居优化策略，整合了图像识别信息用于高维数据集降维。Mod-LLE在低维数据空间中可以获得比较好的内部类分类效果，并保持了高维原始数据固有的拓扑组成信息。实验结果表明，Mod-LLE算法在人脸图像分类算法上有很好的分类效果，在降维效果上优于之前的LLE算法。