《椭圆及其标准方程》教学设计

常洁

一、教学设计

（一）内容和内容解析

1.内容

椭圆这个图形，学生并不陌生，但是仅限于直观的感受，本节在直线与圆的方程之后，再次引导学生用坐标法研究图形，用解析法研究学生熟知的图形，把直观感受上升到可以定性、定量的分析图形.

2.内容解析

圆锥曲线是高中数学中十分重要的内容之一.它的许多几何性质在日常生活、生产和科学技术中都有着广泛的应用.本节是《圆锥曲线与方程》的第一节课，主要学习椭圆的定义和标准方程.它是本章也是整个解析几何部分的重要基础知识.

（二）目标和目标解析

1.目标

通过实验、观察、类比、证明等方法，让学生充分理解椭圆的定义和方程推导，使学生掌握分析、探究、抽象、概括的能力以及用坐标法研究几何图形的方法.

2.目标解析

椭圆及其方程是在坐标法研究几何图形中起着承上启下的作用.首先，学生已经有了圆这个几何图形和方程这个代数表达之间的一一对应关系，但是又没有深入讨论如何建立起图形和方程之间关系的一般方法.本節内容从建系开始，到得到方程结束，每一个过程都充分让学生参与、体会，从而为学生后期掌握研究其他圆锥曲线的方法和能力打下了坚实的基础.

教学重点：椭圆的定义、椭圆标准方程的推导.

教学难点：椭圆标准方程的推导.

（三）教学支持条件分析

（1）通过课前微课，让学生了解圆锥曲线名称的来历，其中动态演示平面截圆锥，直观感受圆锥曲线的样子.

（2）对椭圆定义的引入，可借助课前学生画图、视频，学生自己动手用图钉绳子，改变绳长，改变图钉间距离，多次演示，直观形象让学生体会椭圆的定义的由来、关键点、该注意的条件.

（3）注意椭圆的定义与椭圆的标准方程的联系.

（4）推导椭圆的标准方程时，可利用多媒体辅助工具，让学生类比圆的方程的求解方法，得到求椭圆标准方程的建系方法.

（5）利用多媒体辅助翻转图形，启发学生得到焦点在y轴上的椭圆的标准方程.然后，鼓励学生探索椭圆的两种标准方程的异同点，进一步加深对椭圆的认识.

二、教学过程

（一）直观感受，复习旧知

回忆圆与方程的有关知识，共同观看同学做的小实验视频.

视频片段1：根据圆的定义画圆.

用图钉确定一定点，固定绳长，画出圆.

提问全体学生，共同回忆圆的定义，强调“一定点”“一定长”，动点的轨迹为圆.

（二）新课教学

1.椭圆的定义

视频片段2：探索画出椭圆的条件

问题1：类比圆的定义，视频中的同学还尝试了将这一定点，一定长做了怎样的变化？她画出了什么图形？

学生思考后回答：她将一定点变成了两定点，定长变成了动点到两定点的距离之和为定长，然后画出了椭圆.

问题2：若保持两定点间的距离不变，加大绳长，动点的轨迹还是椭圆吗？

学生得出结论：还是椭圆.

问题3：是不是确定任意的定点和定长画出的都一定是椭圆？

若保持两定点间的距离不变，缩短绳长，使它恰好等于两定点间的距离，动点的轨迹还是椭圆吗？

老师追问，学生思考后回答：画不出椭圆，因为笔尖无法旋转了，但可以移动，因此轨迹为线段.

问题4：若保持两定点间的距离不变，缩短绳长，使它短于两定点间的距离，动点的轨迹还是椭圆吗？

学生思考后回答：画不出轨迹.

通过探索便可发现，当绳子的长度大于两个定点间的距离时，将铅笔卡在绳子上拉直，再旋转一周，所得到的图形便是椭圆形了.得出结果后，教师可就圆的绘制及椭圆的绘制过程及结果进行板书对比总结，加深学生的印象，也为后续问题做铺垫.

设计目的：让学生对所掌握的知识重新进行归纳及整理，能大胆猜想，敢于实践，培养他们的探究精神.

焦点及焦距的定义：椭圆的两个定点通常称为椭圆的两个焦点，两个焦点间的距离称之为焦距.

2.椭圆的再认识

设椭圆的两个焦点分别为F1，F2椭圆上任一点M，能否从以上绘制出的椭圆图形中，抽象出一个等量关系，并由此归纳椭圆的定义？

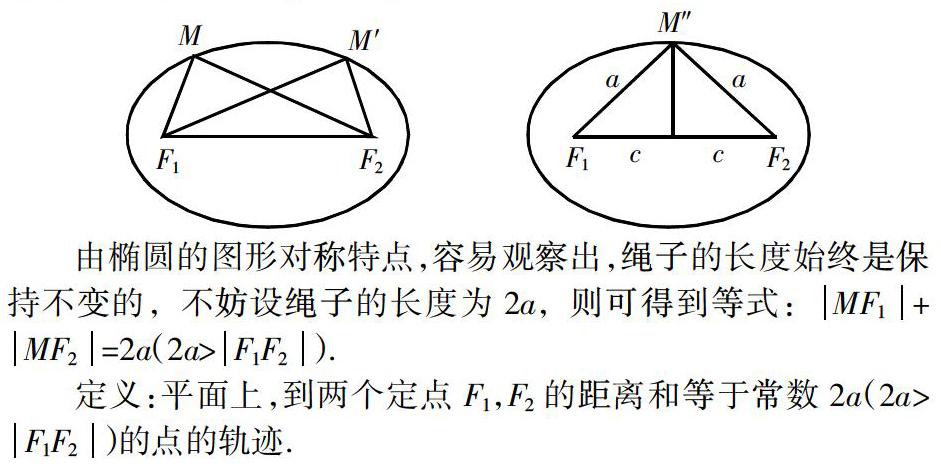
问题1：观察椭圆，根据定义，在椭圆上任取一点M，它到两定点的距离和等于定长，也可以想象成绳长，那么，当改变动点M的位置，它到两焦点的距离有变化吗？有没有这样一个特殊的点M的位置，恰好把绳长分成两等分？

由椭圆的图形对称特点，容易观察出，绳子的长度始终是保持不变的，不妨设绳子的长度为2a，则可得到等式：MF1+MF2=2a（2a>F1F2）.

定义：平面上，到两个定点F1，F2的距离和等于常数2a（2a>F1F2）的点的轨迹.

设计目的：锻炼学生的观察能力，培养学生抽象概括的能力.

3.椭圆标准方程的推导

我们知道，对于几何图形的研究如果想更加准确深入，就不能停留在只观其形的感性认识，还要用科学严谨的代数结论来加以论证.那么，你能仿造对圆的研究，找到椭圆这样一个几何图形对应的代数方程吗？

引导学生回忆求曲线方程的基本步骤：建系、设点、列式、化简、检验.

讨论建系方案：

启发学生类比求圆的方程的建系方法，建立适当的直角坐标系.学生可能会有如下几种建系方案：

方案1：以定点F1为原点，两定点的连线为x轴;

方案2：以两定点的连线为x轴，其垂直平分线为y轴;

方案3：以两定点的连线为y轴，其垂直平分线为x轴.

根据建系原则中的简洁性、对称性标准.

选择以方案2为例，推导椭圆的标准方程：

①建系：以F1，F2所在直线为x轴，以线段F1F2的垂直平分线为y轴，建立直角坐标系.

②设点：设M（x1，y）是椭圆上任意一点，为了使F1，F2的坐标简单及化简过程不那么繁杂，设F1F2=2c（c>0），则F1（-c，0），F2（c，0）

设M与两定点F1，F2的距离的和等于2a

【难点突破】学生对含有两个根式之和的等式进行化简有一定困难，可采用以下方法突破难点：首先让学生明确，含根号的等式化简的目的就是要去掉根号，变无理式为有理式;其次复习含有一个根式的等式的化简方法——将根式放在等式的一边，其他项移到等式另一边，两边平方可去掉根号;有了这一基础，可启发学生，化简含两个根式之和的等式，只要将两个根式分别放在等号两边，其中一边只含一个根式，平方一次后即可转化为只含一个根式的化简问题.

表格全面总结：椭圆定义，焦点在x轴和y轴上的椭圆的图形及方程的相同点和不同点，强调已知椭圆标准方程，如何判断焦点位置？

引导学生思考：看x2，y2的分母大小，哪个分母大就在哪一条轴上，简记为“大分母定焦轴”.

设计目的：通过对比总结，强化不同类型的方程的异同，从而深化学生对椭圆标准方程的理解;通过讨论，学生自主学习，构建新的知识体系，不但能学习到真正属于自己的、可灵活运用的知识，而且在此过程中掌握求知的方法，深化学生对椭圆标准方程的理解.

（三）典型例题研究

例1.列方程是否表示椭圆？

设计目的：使学生进一步熟悉椭圆的标准方程，在辨别中加深印象，加强对知识的理解.

【想一想】你还能用其他求它的方法吗？哪种方法更简单？你有什么体会？

设计目的：教师平板展示，强调解题的规范.并让学生熟练椭圆标准方程的运用.让学生知道用待定系数法也可以解决这道题.

（四）课堂小结

1.橢圆的定义

2.椭圆的标准方程（注意焦点的位置与方程形式的关系）

（五）作业布置

课本42页练习1、2;49页习题2.2A组1、2

板书设计目的：条理清晰，把本节课的重点、难点写在黑板最突出的地方，便于不断强化学生对本节课知识的掌握.

编辑 鲁翠红