基于数学思想渗透的核心素养提升——《最基本的图形：点和线》复习课教学设计

林奕杰

(福建省泉州市厦门外国语学校石狮分校 362799)

一、目标

1.知识与技能

(1)复习并使学生会画出、会表示直线、射线、线段，理解它们的性质意义，能说出它们的不同；

(2)复习并使学生能说出两个基本数学事实，会用两个基本事实进行生活现象的判断与简单几何推理依据；

(3)复习并会利用尺规作图作一条线段等于已知线段；

(4)会根据要求测量线段、比较线段的大小，理解线段的和差，会根据图形直观利用线段的和差求解线段的长；

(5)理解线段中点的意义，掌握数轴上中点公式，两点间的距离公式，会用它们求解.

2.数学思考

(1)通过对基本图形及线段和差的观察形成初步的几何直观；

(2)通过观察、猜想、推理计算过程的书写，发展合情推理与演绎推理；

(3)渗透分类讨论、方程、设而不求、数形结合、整体等数学思想.

3.问题解决

会判断直线、射线、线段，会根据几何描述画相应的图形，能运用线段的和差、中点公式、距离公式计算，会用两个数学事实解释.

4.情感态度

培养学生空间想象能力、抽象思维能力，培养学生对几何的兴趣，提高数学的应用意识.

二、重难点

重点：线段的和差计算；难点：运动中数量的分析.

三、过程

(学生操作1)：在平面内画任意点P(教师也在黑板上展示).

(设问1)：点是如何表示的？有无大小？数学的‘点’与生活中的‘点’一样吗？

(设问2)：过P可以画几条直线？射线？线段？

(设问3)：你可以从哪些角度来说明点和线的关系？

【设计意图】本操作‘大撒网’，从最基本的画点、表示点入手，再由点过渡到线，起点低，易于学生入手思考从而激发学生的学习兴趣.知识层面上复习了点、点的表示、点与线的关系.

(设问3)引导学生从运动和集合两个方面来思考理解点和线的关系，从一个全新的角度、更高的视角来审视原有的知识，既不会让学生觉得炒冷饭，又让学生重新构建了知识.

这三个设问渗透了运动变化、类比、集合、有限与无限等数学思想；关注了几何直观和数学抽象等核心素养.

(学生操作2)：在操作1的基础上把点P向右移动一定距离得点Q，画直线PQ.

(设问4)：画直线应注意什么？可以画几条直线？直线PQ和直线QP是同一条吗？这说明了一个什么数学事实？

(设问5)：从学过的直线、射线、线段的知识角度，根据图你能提出什么新的问题？

【设计意图】：本操作在操作1的基础上进一步复习了点的平移，直线、射线、线段的画法、表示及三者的区别联系，复习了基本事实“两点确定一条直线”，渗透了运动变化、类比、分类讨论等数学思想.设问5让学生根据所学知识结合动手操作获得的图形自由提问，一方面有利于学生在提取旧知识的同时重新构建新框架、保持思维的开放性，另一方面又化被动为主动，利用学生资源，让不同水平的学生都可以参与，使课堂不再沉闷，达成“跳一跳摘到果子”的螺旋上升效果，让学生成为课堂主人，不同的学生都有获得感，激发他们的数学学习兴趣和信心.

(学生操作3)：在操作2的基础上在直线PQ外任取点M，连接MQ、PM，并测量出线段PQ的长(精确到0.1cm).

(设问6)：比较大小PQ+PM____QM;PQ+QM____PM;PM+QM____PQ.

(设问7)：这说明了哪个数学基本事实？P、Q两点的距离是多少？能否说线段PQ就是P、Q的距离？

(给出距离的定义，特别注意语言的描述：距离是长度不是图形)

【设计意图】本操作从操作1的‘大撒网’开始收缩，从‘形’逐渐过渡到‘数’，旨在复习线段的测量、基本事实“两点之间线段最短”、两点间的距离，辨析了‘距离’是个长度数据而非图形.本操作渗透了数形结合的思想，进一步培养学生数据分析、几何直观等素养.操作1到操作3都是在复习基本概念、基本性质、基本事实，属于基础知识的重现，用一条线窜起来从不同角度去思考、比较、辨析，又重构了这些知识，从数学思想方面形成新的知识结构.

(学生操作4)：尺规作图：在操作3的基础上作线段AB，使得AB=PQ+QM+PM,并在线段AB上取点C.

(设问8)：线段AC、BC、AB满足什么样的数量关系？请表示出来.

(设问9)如果AB=10，AC是BC的3倍，求AC.(你有几种方法？)

(变式1)：如果线段AB=10，C是直线AB上一点，且AC=3BC，求BC.

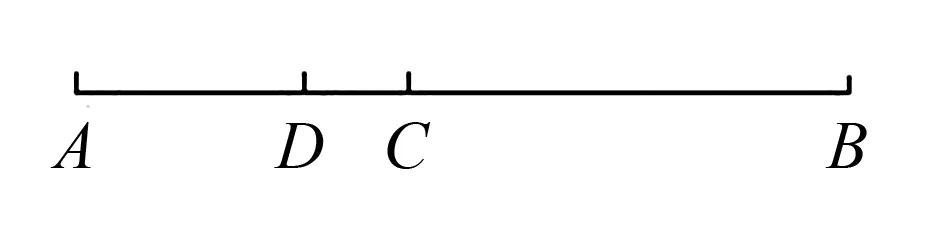
(变式2)如图，线段AB上有C、D两点，点C将AB分成5：7两部分，点D将线段AB分成5：11两部分，若CD=15cm，求AB.

(变式3)：如果线段AB=10，C为线段上一点，M、N分别是AC、BC的中点，AC=6，求MN的长.

(变式4)如果线段AB=10，C为线段上一点，M、N分别是AC、BC的中点，求MN的长.

(引导学生用两种方法求解，渗透设而不求、整体思想)

(分析小结)请注意：已知条件不但包括文字部分提供信息，也包括图形中提供的直观信息(比如本题中线段的和差)，要会看图，用图；要会用不同的代数式表示同一个量列方程，比如本题中用两个量表示线段AB的长.

(变式5)：A是数轴上表示-3的点.

①如果A向右移动10个单位得B，则B所表示的数为____，C为AB中点，则C所表示的数为____；

②如果A向右以2个单位/秒的速度运动得B，t秒后B所表示的数为____(用含t的代数式表示)，C为AB中点，C所表示的数为____(用含t的代数式表示).

B点表示的数为7，C点从原点出发，以3个单位/秒的速度向右运动，同时，B点以1个单位/秒的速度向右运动，运动时间为t秒，t为多少秒时，A、B、C三点中，一点是另外两点的中点？

【设计意图】本操作是本节知识考试的热点和难点，是本节课升华与高潮部分.在前面三个操作复习了点、线基本概念、基本事实的基础上，复习了线段的和、差、倍、分及中点的计算，涉及到了合情推理和演绎推理.本操作通过五个变式，结合点在数轴上的运动，从数字到字母、由静止到运动、从单一到多样，层层推进、螺旋上升，揭示了知识间的内在联系，通过一题多解、多解归一，探究了解决此类问题的一般方法，形成知识模块，即照顾了一般同学的水平让他们有所发展，又照顾了学有余力同学提升能力的需要，进一步培养了学生分析问题、解决问题的能力.让每个同学在最近发展区内有所获得.本操作渗透了运动变化、分类讨论、方程、设而不求、数形结合、整体等数学思想.

【设计小结】本节课是一节复习课，选自华东师大(2012)版七年级上册第四章的4.5《最基本的图形——点和线》.第四章《图形的初步认识》是以发展学生的空间观念和几何直观为核心的，“点和线”这一节，是让学生在小学的学习基础上，对几何图形最基本的元素有进一步的认识.点和线是最基本的图形，小学已学过相关的知识，这些概念来源于客观实际，是对客观物体的抽象，初中再来学习，特别是作为一节复习课，就要挖掘本课内容所隐含的运动变化、分类讨论、方程、设而不求、数形结合、整体等数学思想，利用本节丰富的数学思想进一步培养学生的几何直观、推理计算、合情推理与演绎推理等数学数学素养.

对于初一的学生而言，本节课的知识零散，涉及的数学思想繁多、数学推理抽象.华罗庚先生说：“把厚书读薄，把薄书读厚.”又说：生书熟讲，熟书生温.前者说的是理念，后者讲的是方法.复习课如何做到让‘熟书生温’，笔者思考那就要从另外的‘新途径’把‘旧知识’窜起来.所以知识层面上笔者用一条线：‘画点、表示点——点到线——画线、表示线——点和线的基本事实——线段的计算’把这部分知识技能重新组织起来，从不同的角度让学生感受到‘新’意；在数学素养方面，笔者深入挖掘本节所涉及的数学思想，通过渗透数学思想来提升知识境界，让学生有‘新视野’达成提升学生数学素养的目标；在教学方法层面上，笔者采用变式教学，层层设问，开放编题，螺旋上升，让更多的学生参与，使学生的思考是主动而非被动、多样而非有限，思维是开放而非封闭、积极而非懈怠；让学生达成自我发展.