一种基于最大公共子图的社交网络对齐方法*
冯 朔, 申德荣, 聂铁铮, 寇 月, 于 戈
(东北大学 计算机科学与工程学院,辽宁 沈阳 110819)
随着 Internet的广泛普及,各类社交网络走进人们的视野,不同社交网络为用户提供了不同的社交服务,例如,豆瓣为用户提供了图书、电影、音乐交流分享服务,知乎为用户提供了问答服务,微博为用户提供了分享动态的服务,用户为满足不同的服务需求,往往不会局限于单一社交网络中,而是在多个社交平台中注册账号,因此,社交网络对齐问题(通常也称为用户识别问题、用户匹配问题、网络反匿名化问题以及锚链接预测问题)逐渐引起了学者的关注.网络对齐将有效集成分散于各个网络中的用户资源,将大大提高用户推荐、广告投放、用户组形成等以用户为中心的服务质量.
针对网络对齐问题,在早期研究工作中,研究者们主要利用用户E-mail[1]、用户真实姓名[2]等信息进行识别,虽然依据E-mail和真实姓名能够精确匹配用户,但在真实社交网络中,E-mail和真实姓名由于隐私保护的原因,通常难以获取[3].因此,现阶段工作主要集中于利用:(1) 用户属性信息,如用户头像、用户喜好等[4,5];(2) 用户行为信息,如发帖关键字、用户行为轨迹等[6,7];(3) 用户结构信息,如用户朋友关系、用户与帖子的评论关系等[3,8,9].虽然现有方法具有良好的准确性,但真实社交网络通常面临用户数据匿名化严重、部分用户数据难以获取等问题,且现有公开数据也面临数据缺失、数据不一致、数据分布不均、数据异构等问题.
本文利用用户结构信息研究网络对齐问题,相比于用户属性信息与行为信息,用户结构信息具有易获取、易识别的特点,例如,人人网中用户的朋友关系、微博用户的关注与被关注关系以及大部分社交网络中用户之间的互动关系,均可作为标识用户的重要依据.但这并不意味着用户属性信息以及用户行为信息是无用的,在处理真实数据的过程中,本文可结合用户属性信息和用户行为信息,以取得更准确的用户识别效果.
网络对齐问题可抽象为最大公共子图问题(α-MCS)[10-12],如图 1所示,G,G′表示两个不同的社交网络,节点表示用户,实线边表示图中用户之间的朋友关系,α-MCS的目标是求取G到G′的映射函数F,使得Sco(F)=#重叠边数量-α#非重叠边数量,取值最大,其中,α表示平衡重叠边与非重叠边数量的参数.例如,当α=0时,对于F1={(1,b),(2,a),(3,f),(4,e),(5,d),(6,c)},Sco(F1)=8,不存在其他映射关系F2使得Sco(F2)>Sco(F1),因此,称由F1形成的公共子图为G,G′的最大公共子图.
传统的最大公共子图问题在解决网络对齐问题时,存在以下几点不足:首先,其参数α无法自适应于不同类型网络,传统方法主要依赖于启发式的方法确定α,然而,由于不同网络结构的不同,使得该类方法具有一定的局限性;其次,传统方法计算复杂度较高,这类算法通常只能处理数据量较小的网络,随着社交网络规模的扩大,现有算法已不再适合处理大规模数据的社交网络;此外,现有方法的目标通常追求代价函数最小的匹配结果,而非社交网络用户的真实匹配关系,并没有结合社交网络结构特征有效地解决问题.因此,本文针对现有方法的不足,提出基于最大公共子图的社交网络对齐方法,主要有以下贡献点.
1) 本文利用最大公共子图问题(α-MCS)对网络对齐问题进行求解,并针对参数α的取值进行讨论,使其自适应于不同社交网络结构.
2) 为快速地解决α-MCS,本文提出基于最大公共子图的迭代式网络对齐算法 MCS_INA,主要分为两个阶段:第1个阶段,分别在两个社交网络中选取易于识别的候选匹配用户集合,第2个阶段,针对候选匹配用户集合进行识别.相比于传统方法,该方法结合社交网络特征,通过参数估计,快速定位候选集,降低了算法复杂度,该算法复杂度为O(DD′(D+D′)(|V|+|V′|)),远小于现有方法,其中,D,D′分别表示G,G′的平均度数,V,V′表示G,G′的用户集合.
3) 为验证 MCS_INA的有效性,本文选择在真实数据集和合成数据集上进行实验,实验结果表明,MCS_INA在识别准确率与召回率上明显优于现有算法.
本文第1节简述相关工作.第2节简述相关预备知识,包括符号定义以及网络对齐模型.第3节针对α-MCS中参数α进行讨论,求取自适应的参数α.第4节提出算法MCS_INA,以有效解决α-MCS.第5节设计并展示实验结果,分析算法的有效性.第6节对本文进行总结.
1 相关工作
现阶段网络对齐方法可分为 3类:基于用户属性信息的网络对齐方法、基于用户行为信息的网络对齐方法、基于用户结构信息的网络对齐方法.
在网络对齐领域中,最传统的方法是利用用户真实姓名和 E-mail进行用户识别,该类方法通过衡量字符串之间的转换规则以及相似性进行用户识别.然而,用户名和E-mail在具有较高识别准确性的同时,大大降低了召回率.因此,部分学者利用额外的用户属性信息进行网络对齐.虽然额外属性信息的加入提高了用户识别的召回率,但真实网络数据中用户属性信息往往具有隐私性、异构性,研究者获取到的数据往往是不全面的,甚至是错误的.
基于用户行为信息的对齐方法认为用户在不同社交网络中表现出相似的用户行为特征,例如用户写作习性、用户登录时间地点特征、用户主题偏好等.传统方法主要通过提取用户行为特征相似性进行用户识别,例如文献[13]针对用户写作特征,从用户词汇特征、语义特征、文章结构特征、文章主题特征进行特征抽取;文献[6]分别从“用户-时间”“用户-空间”“用户-关键字”3个方面进行用户特征提取.通过计算用户行为特征相似性,大部分已有方法将网络对齐问题转化为二分类问题,并利用 SVM、逻辑回归、稳定婚姻匹配等分类方法进行识别.
基于用户结构信息的网络对齐问题,可抽象为最大公共子图问题.该问题最早在文献[14]中提出,作者认为重叠边数量是衡量最大公共子图问题的唯一条件,而文献[10]认为最大公共子图问题需要综合考虑重叠边数量与非重叠边数量.传统的最大公共子图问题均为 NP完全问题,后续大量文献针对最大公共子图问题进行了近似求解,但现有近似求解方法的复杂度均大于O(nlogn),并不适用于真实网络环境.
为了解决真实网络环境下的网络对齐问题,文献[15]认为,少部分已知匹配用户可显著提升网络对齐的准确性,该文献通过部分节点迭代地识别其余用户;之后,文献[16]在有权重图上提出基于随机游走的用户相似性算法;文献[17]针对大规模网络上时间代价过高的问题,以牺牲部分召回率为代价,有效降低了时间复杂度,文献[3]有效解决了无已知匹配用户情况下的网络对齐问题.这些方法均利用网络结构特征,通过求取用户相似性,选择匹配用户.
此外,部分学者提出了基于网络表示的网络对齐算法.文献[18]将用户映射到多维空间中,他们认为不同网络中相同用户在该空间中距离相近;文献[19]对有向网络中的用户进行识别,其用户映射函数与用户自身属性、父母属性、孩子属性相关.此外,文献[20]认为,映射函数同样与用户所处社群相关.
然而,以上算法均为启发式算法,文献[8]首次提出了网络对齐模型,网络对齐模型是描述现实社交网络用户关系的数学模型,文献[8]中证明了其算法的正确性,并在现实网络对齐问题中取得了较高的准确率.之后,文献[9]在此基础上,通过增加匹配迭代次数,显著提升了准确率与召回率,文献[21]证明了其方法在无标度网络对齐模型中的正确性,文献[22]针对已知匹配用户过少的情况,以降低准确率为代价,提升了部分召回率.
本文方法与已有方法不同之处有二.首先,本文利用网络对齐模型,对最大公共子图问题中参数取值进行讨论,给出严谨的理论推导过程,相比于传统启发式确定参数的方法,本文方法可自适应于不同类型的网络;其次,本文在解决网络对齐的过程中,借鉴最大公共子图思想与网络对齐模型,结合社交网络特征,通过参数估计,快速定位候选集,有效降低了算法复杂度,本文算法的计算复杂度远小于现有方法.
2 预备知识
2.1 符号和定义
定义1(网络).给定网络G(V,E),其中,V表示网络G中用户集合,E表示网络G中用户关系集合,若用户i与用户j之间存在边,则表示Vi,j=Vj,i=1,否则,Vi,j=Vj,i=0,对于网络中节点i,本文使用表示该节点i所对应的用户个体.
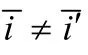
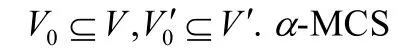
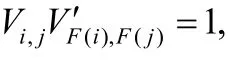
例如,如图1所示,令α=1,初始映射函数F0={(2,a),(3,f)},则G,G′的最大公共子图F为F={(1,j),(2,a),(3,f),(4,g),(6,i)},其中,重叠边为(4,1),(4,3),(3,6),(3,2),(2,1),(6,1),无非重叠边,因此,公共子图F的得分为Sco(F)=6,而对于其他任意公共子图,其Sco得分均不可能超过6.因此,公共子图F为G,G′的最大公共子图.
2.2 网络对齐模型
网络对齐模型[8]在跨社交网络分析的过程中具有重要意义,该模型认为现实中不同的社交网络均源起于相同的网络,即对于任意对齐网络G和G′,均源起于一个潜在网络G*,其中,G*描述了用户之间的全部社交关系.依据此假设,网络对齐模型可描述为两个独立的过程:(1)G*的模型化,本文假设G*(V*,E*)满足,对于任意i*,j*∈V*,i*与j*之间存在边的概率为pi*,j*,本文不针对pi*,j*附加任何约束条件,即网络G*可满足均匀分布(如 ER模型[23]),也可满足幂律分布(如 Stochastic blockmodels[24]).(2) 真实网络G,G′的产生:本文假设对齐网络G和G′均为网络G*的子图:对于G*中任意一个节点,其有SV的概率出现在网络G中,有SVʹ的概率出现在网络G′中;而对于网络G*中任意一条边Vi*,j*=1,若节点i*,j*已存在于在G中,则该边存在于G中的概率为SE.同理,若节点i*,j*已存在于在G′中,则该边在G′中存在的概率为SEʹ.
3 最大公共子图自适应参数分析
本节着重针对最大公共子图问题中参数α的取值进行分析,依据公式(1),公共子图F得分的期望值为
其中,Pr(Vi,j,V′F(i),F(j))表示边Vi,j与边V′F(i),F(j)均存在的联合概率,Pr(Vi,j,¬V′F(i),F(j))表示边Vi,j存在且边V′F(i),F(j)不存在的联合概率.
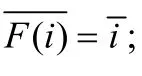
证明:依据定理1的描述,仅需证明存在α,使得以下两个条件成立:
4 基于最大公共子图的迭代式网络对齐算法
在第3节中,本文讨论了最大公共子图问题中参数α的取值,本节将提出基于最大公共子图的迭代式网络对齐算法MCS_INA(α-MCS based iterative network alignment algorithm),如算法1所示.
算法 1.MCS_INA(G,G′,F0).
输入:G,G′,F0;
输出:F.
给定对齐网络G和G′以及初始匹配用户关系F0,MCS_INA的输出是包含F0的用户对应关系F.首先,算法利用初始匹配用户集合F0初始化输出集合F(第1行),之后,迭代地利用已匹配用户识别其他用户.在每次迭代过程中,主要分为两步:第1步,分别从G和G′中选取识别度较高的候选匹配用户集合C,C′(第3行~第4行),为降低计算复杂度,该步骤分别针对两个网络G,G′单独进行处理,选取与已匹配用户关系较近的用户集合;第2步,分别针对候选匹配用户集合C,C′进行用户匹配,借鉴最大公共子图思想,构建匹配用户映射关系M:V→C′和M′:V′→C(第5行~第6行),并将M与M′重叠的部分作为匹配结果(第7行),加入到输出集合F中,并执行下一次循环,若连续两次迭代匹配结果F未发生改变,则停止迭代,将F作为算法的输出.
本文在第4.1节中将深入讨论候选用户集合选取问题;在第4.2节中将深入讨论候选用户集合匹配问题.
4.1 候选匹配用户选取策略
为便于描述,本节仅针对G中候选匹配用户选取问题进行讨论.给定网络G(V,E)以及已匹配用户映射关系F,候选匹配用户选取算法Candidate(G,F)的目标是,在G中选取与匹配用户集合VF关系紧密的用户群体C.结合最大公共子图思想,对于用户k,构建其代价函数如下:
公式(5)中,SE(本文仅对SE进行分析,SEʹ同理)、Pr(Vi,k)、α均为未知参数,下面将对这些参数进行分析估计.
首先,SE表示网络对齐模型中网络G*中的边保留到G的概率,可通过以下公式进行估计:
其次,Pr(Vi,k)表示G中用户i与k之间存在边的可能性,可通过i,k之间的间接关系进行预测,本文认为Pr(Vi,k)与用户i与k的共同邻居数量相关.
其中,N(i)表示用户i的邻居集合,δ(p,q,|N(i)∩N(k)|)表示用户对p,q的共同邻居数量是否等于|N(i)∩N(k)|的判断.若相等,则δ(p,q,|N(i)∩N(k)|)取值为 1;否则,δ(p,q,|N(i)∩N(k)|)取值为 0.公式(7)的分子部分表示网络中公共邻居数量为|N(i)∩N(k)|且存在边的节点对数量,分母为网络中公共邻居数量为|N(i)∩N(k)|的节点对数量.显然,若网络中大部分公共邻居数量为|N(i)∩N(k)|的节点对之间存在边,则Pr(Vi,k)取值应该较高,否则,Pr(Vi,k)取值较低.
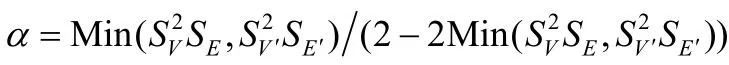
算法 2.Candidate(G,G′,F).
输入:G,G′,F;
输出:C.
在算法2中,首先,利用公式(6)对参数SE,SEʹ进行估计,并赋值β=1(第1行).之后,利用已识别用户集合VF,获取待分析的候选匹配用户集合Tmp(第2行~第5行),从第6行开始,迭代地分析Tmp中用户是否适合作为候选匹配用户.若对于用户i∈Tmp-VF,其ΔScoE(i)>0,则认为用户i适合作为候选匹配用户,并将其放入候选匹配用户集合C中(第9行~第12行),并输出结果集C.若结果集C为空集,则有可能参数β取值过高,降低参数β,并重新计算候选匹配用户集合(第 15行).在算法 2中,通过迭代降低参数β,可有效提高算法识别精度,初始情况下,β取值为 1,相对应的α取值较高,候选匹配用户集合选取相对严格.而随着迭代的进行,β取值逐渐降低,进而α取值随之降低,候选匹配用户集合选取逐渐宽松,最终,当β取最低值时,若候选匹配用户集合依然为空,则无适合匹配的用户.
通过算法 2,可获取有序的候选匹配用户集合C,集合C中用户依据与已匹配用户之间的关系强度进行排序,与已匹配用户关系紧密的用户具有较高排名,相反地,关系疏远的用户具有较低排名.另外,对于每个候选匹配用户,计算其代价函数的时间复杂度为O(D2).因此,在MCS_INA中,候选匹配选取算法Candidate(G,G′,F)的时间复杂度为O(D2|V|+D′2|V′|).
4.2 用户匹配策略
给定G中候选匹配用户集合C,用户匹配算法Match(G,G′,F,C)的目标是,构建映射函数M′:V′→C.由于最大公共子图问题为 NP完全问题,为降低计算复杂度,本节利用第 4.1节中候选匹配用户排名,结合贪婪思想,提出近似求解算法.
对于候选匹配用户集合C中任意用户k∈C,令k′为G′中未匹配用户,借鉴最大公共子图思想(见公式(1)),则k′与k的匹配度可表示为
公式(8)表示,若匹配用户k与k′,可提升匹配结果Sco得分ΔSco(k,k′).
至此,用户匹配算法Match(G,Gʹ,F,C)如算法3所示.
算法 3.Match(G,G′,F,C).
输入:G,G′,F,C;
输出:M.
算法3中采用贪婪思想有序地对用户集合C中用户进行识别,优先识别与已匹配用户关系紧密的用户,可有效降低识别错误的发生.
在算法3中,对于每个候选匹配用户k,其对应的Tmp集合中用户的个数为O(DD′),而对于Tmp中每个用户t′,计算k与t′匹配度的时间复杂度为O(D+D′),因此,识别每个候选匹配用户k的时间复杂度为O(DD′(D+D′)),且在 MCS_INA 中,用户匹配算法Match(G,G′,F,C)的时间复杂度为O(DD′(D+D′)(|V|+|V′|)).
综上,算法 MCS_INA 的时间复杂度为O(DD′(D+D′)(|V|+|V′|)).
5 实 验
5.1 实验环境
实验环境:本文采用Java编程语言实现相关算法,实验主机采用Intel i5-4590处理器,主频3.30GHz,8GB内存,操作系统为64位Windows 7.
数据集:本文所使用数据集见表1.首先,Facebook表示匿名化的真实Facebook数据集,其中,第1个网络(FL)为Facebook新奥尔良市用户关系网络,另一个网络(FW)为Facebook新奥尔良市用户信息墙交互网络,其中,重叠的用户数量为25 538,重叠的边的数量为151 580,该数据集可参考文献[25];其次,本文利用真实社交网络生成部分数据集,其中,Twitter表示真实Twitter用户数据集,T1.0表示原始的Twitter数据规模,T0.8表示T1.0中80%的边以及80%的节点被保留到数据集T0.8中,T0.7和T0.9同理.在生成T0.7、T0.8和T0.9时,均采用随机概率保留点和边.另外,本文采用不同随机图生成算法生成合成数据集ER和PA,其中,ER表示该网络分布满足ER随机图模型[23],PA表示该网络节点关系分布满足幂律分布[26],所有随机图均通过igraph生成.最后,本文随机地选取匹配用户作为已知匹配用户,该方式将有效降低识别瓶颈的发生,若已知匹配用户集中于单一社区内,将造成社区外部节点识别准确率的下降.
对比算法:由于启发式的解决方法适用性较低,与本文研究内容有差异;基于网络表示的网络对齐算法,需要大量训练数据,而本文方法仅基于预先匹配的少量用户节点数量(占比通常为 10%以下),两种方法环境不同.为此,本文仅选取与本文研究方法密切相关的两种经典算法CN和CNR进行比较:(1) CN[8]:CN算法为迭代算法,每次迭代过程中,选取共同邻居数量最多的用户对作为匹配用户;(2) CNR[9]:与CN算法类似,但CNR算法在每次迭代过程中优先匹配度数较高的用户;(3) MCS_INA:本文提出的算法.
效果评价:本文采用准确率(precision)、召回率(recall)、F-measure以及运行时间(runtime)这4个方面进行评估.
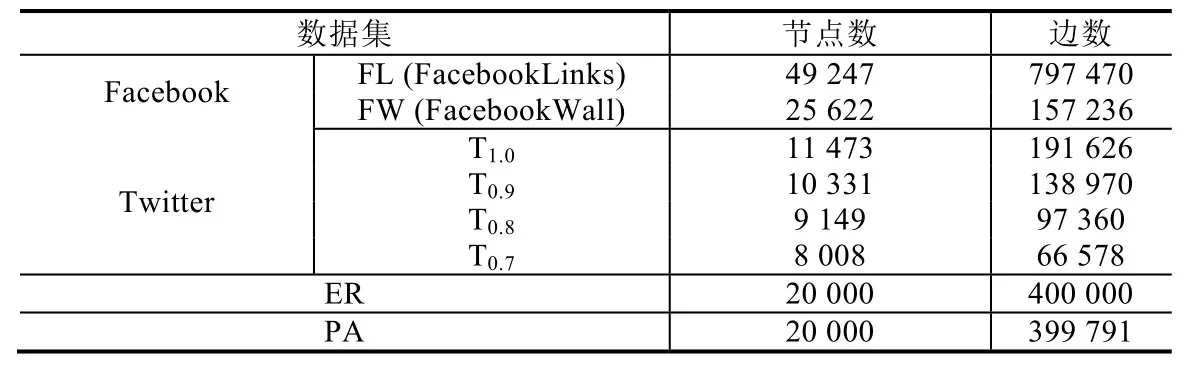
Table 1 Datasets表1 数据集
5.2 真实数据集中的实验效果
首先,为比较不同算法在不同数据集中的识别准确率,该组实验采用 FL&FW、T0.7&T0.8、T0.7&T0.9和T0.8&T0.9这4个数据集,对于每组数据集,随机地选取10%的匹配用户作为已知,实验结果如图2所示.在3种不同算法中,本文算法MCS_INA的准确率最高,而CN算法准确率最低.另外,对比Twitter的3组数据集,3种算法在数据集T0.8&T0.9上具有较高准确率,而在T0.7&T0.8数据集上具有较低准确率.原因是,T0.8&T0.9重叠用户数量以及重叠边较多,期望情况下其重叠边为T1.0边数量的37%,而T0.7&T0.8的重叠边比率仅为17%.因此,T0.8&T0.9相对更容易识别.
其次,对比不同算法在不同数据集中的召回率,如图3所示.在3种算法中,本文算法MCS_INA的召回率依然最高,其次为 CNR,算法 CN 召回率最低;对比图 2中的准确率,算法 CNR 在数据集 T0.7&T0.8、T0.7&T0.9、T0.8&T0.9中的召回率略高于准确率,这是由于 Twitter数据集中包含大量单独存在于单个网络中的用户,算法CNR错误地识别了这一部分用户.而在数据集FL&FW中,算法CNR的准确率略高于召回率,这是由于FW数据集几乎为FL数据集的子集.
最后,综合准确率与召回率,F-measure的比较结果如图4所示,MCS_INA的综合性能明显优于算法CN和CNR.
为测试不同算法在不同数据集中的运行时间,本组实验记录了不同算法的运行时间,见表2.由表2可知,算法CN的运行时间最短,其次为MCS_INA,CNR的运行时间最长.虽然算法CN具有最短的运行时间,但综合图4中F-measure的比较结果来看,MCS_INA依然具有最高的综合性能.另外,对于算法CNR,无论从算法执行时间还是算法精度,MCS_INA均优于CNR.

Table 2 Runnin time on real-world datasets (min)表2 真实数据集中运行时间比较结果 (分钟)
5.3 合成数据集中的实验效果
在第5.2节中,本文针对真实数据集进行了实验,虽然在真实数据集中算法MCS_INA具有较优性能,但并不代表在所有数据集中算法 MCS_INA均表现优异,为此,在第 5.3节中,本文利用不同类型的合成数据集,测试算法的性能.
1) MCS_INA在不同类型网络中的性能实验
为验证算法MCS_INA在不同类型数据集中的表现,本节分别在ER数据集与PA数据集中测试MCS_INA算法的性能,见表3和表4.以ER数据集为例,数据集ER0.5、ER0.6、ER0.7、ER0.8、ER0.9分别表示从数据集ER中以概率[0.5,0.6,0.7,0.8,0.9]提取点和边,对于每组数据集,本实验选取10%的用户作为已知匹配用户.由表3和表4可知,当数据集重叠部分较大时(ER0.6&ER0.7、ER0.7&ER0.8、ER0.8&ER0.9、PA0.7&PA0.8、PA0.8&PA0.9),MCS_INA 具有较高的准确率与召回率,而当数据集重叠部分较小时(ER0.5&ER0.6、PA0.5&PA0.6、PA0.6&PA0.7),MCS_INA具有较低的准确率与召回率,其原因是,当数据集重叠部分较小时,非匹配用户之间相似性相对较强,从而错误地匹配非匹配用户,降低了准确率与召回率.另外,对比表3与表4,MCS_INA在ER数据集中的表现明显强于PA数据集,其原因是,ER数据集中用户之间相似程度较低,而PA数据集中,尤其是度数较低用户之间,相似程度较高,当删除部分用户以后,MCS_INA错误地将这些相似度较高的用户进行匹配,从而降低了准确率与召回率.

Table 3 Performance of MCS_INA on synthetic ER datasets表3 MCS_INA在合成ER数据集中的运行结果

Table 4 Performance of MCS_INA on synthetic PA datasets表4 MCS_INA在合成PA数据集中的运行结果
2) MCS_INA运行时间随网络规模变化的实验
为测试MCS_INA运行时间随网络规模的变化趋势,本实验利用ER与PA数据集进行实验.首先,固定合成网络平均度数为 15,变化网络中节点数量,生成不同的原始网络.之后,采用参数SE=SEʹ=SV=SVʹ=0.8,生成对齐网络,实验结果如图 5所示.横轴表示生成网络中节点数量,纵轴表示算法运行时间,可知,随着网络中节点数量的增多,MCS_INA算法的运行时间随网络中节点数量的增加基本呈线性增长.然后,固定合成网络节点数量为 5 000,变化网络中平均节点度数,生成不同的原始网络.之后,采用参数SE=SEʹ=SV=SVʹ=0.8,生成对齐网络,实验结果如图6所示.通过实验可知,MCS_INA算法的运行时间随网络中节点度数的增加呈指数型增长,且MCS_INA处理ER数据集的能力要高于处理PA数据集的能力.
3) MCS_INA性能随已知匹配用户数量变化的实验
本实验数据集采用ER0.8&ER0.8,即依据ER数据集,采用参数SE=SEʹ=SV=SVʹ=0.8生成两组不同ER0.8并对其进行匹配,本实验随机抽取不同数量百分比的用户作为已知匹配用户对,实验结果如图7所示.由图7可知,随着已知匹配用户的减少,实验准确率与召回率逐渐降低,当已知匹配用户数量减少至0.3%时,准确率与召回率实现断崖式降低.这是由于,当已知匹配用户数量降低至 0.3%时,这些已知匹配用户之间几乎不存在直接关系,从而使得MCS_INA的准确率与召回率基本降至0.
4) 参数分析
首先,对自适应参数α进行实验分析,如图8所示,1-MCS_INA表示在每次迭代中不对参数α进行估计,并设定α为 1,同理于 0.5-MCS_INA.该实验分别在 3个不同数据集 ER0.7&ER0.7、ER0.8&ER0.8、ER0.9&ER0.9中运行MCS_INA、1-MCS_INA和0.5-MCS_INA.由图8可知,通过自适应调节参数α,在3个不同数据集中均取得最优性能.另外,0.5-MCS_INA的表现优于1-MCS_INA,其原因是,对于1-MCS_INA,其节点对相似性函数(见公式(8))中参数α过大,很多匹配用户无法达到阈值,使得召回率降低.
其次,针对每次迭代过程中参数α、SE和SEʹ的估计准确性进行分析,本实验采用数据集ER0.8&ER0.8,并记录每次迭代过程中 3个参数值的大小,如图 9所示.对于参数SE和SEʹ,其取值随迭代过程逐渐降低,并维持在 0.8左右.对于参数α,其波动范围较大,在前几次迭代过程中,参数α的取值范围较大,优先对识别度较高的用户进行识别,之后,参数α的取值随迭代过程逐渐降低,并最终稳定在0.4左右.通过理论计算参数α可知,当参数α理论取值0.52时最优(通过定理1可知),之所以会导致实际参数取值与理论取值不一致的情况,是因为在实际情况下,通常有少部分匹配用户,其结构相似性较低,需适量降低参数α的取值.
6 结束语
本文主要针对基于用户结构信息的跨社交网络用户识别问题进行研究.首先,借鉴传统最大公共子图问题,提出了求解自适应参数的方法,使得最大公共子图问题可适用于求解不同类型的网络对齐问题;其次,针对最大公共子图计算复杂度过高的问题,本文提出了基于最大公共子图的迭代式网络对齐算法MCS_INA,相比于传统算法,MCS_INA在每次迭代过程中,仅针对部分候选匹配用户进行匹配,且本文所提出的候选匹配算法有效结合了网络对齐模型,具有严格的理论支持;最后,本文在真实数据集和合成数据集上进行了实验,实验结果表明本文所提出算法具有较高的识别准确率与较低的时间代价.在未来的工作中,将着重针对初始匹配用户过于集中的问题,同时结合用户属性信息、用户行为信息以处理跨网络用户识别问题.

