采用改进Levenberg-Marquardt法的快速弹性运动估计*
宋传鸣, 闵 新, 闫小红, 王相海, 尹宝才
1(辽宁师范大学 计算机与信息技术学院,辽宁 大连 116029)
2(大连理工大学 计算机科学与技术学院,辽宁 大连 116024)
运动估计是一项高效率的去除视频时间域冗余的预测技术,为H.26x、MPEG和AVS等系列编码标准贡献了大部分的性能提升[1,2].然而,多项研究结果表明[1,3,4],仅整数像素精度的运动估计所耗费的计算资源就占编码器全部资源的 40%~80%;若将分数像素精度的运动估计也考虑在内,其运算代价无疑更高.因此,为了在计算复杂度、硬件实现难度和预测精度之间进行折中,现有视频编码标准多年来始终采用了仅能刻画水平、竖直等平移运动的块匹配算法,并陆续提出了多种快速运动估计策略,大致可分为以下7类.
(1) 基于候选向量下采样的策略[5-13]:这类策略的基本思想是只计算搜索窗口中一部分候选向量的匹配误差,从中找出误差最小的向量作为最优运动向量,如菱形搜索、非对称十字多层次六边形格点搜索UMHexagonS、测试域搜索TZSearch和抛物线搜索等.
(2) 基于像素下采样的策略[14-19]:该类策略的基本思想是只计算当前宏块中一部分像素的匹配误差,并将其作为该宏块的误差用于最优运动向量的判断,如多分辨率搜索、梅花形下采样搜索和自适应像素下采样搜索等.
(3) 基于像素预排序的策略[20-23]:此类算法的主要思路是在计算某个候选向量的匹配误差时,优先对当前宏块的较大匹配误差进行累加,当累计误差和大于已知的最小误差时就提前中止该候选向量的判断,从而达到降低计算量的目的,如部分失真搜索等.
(4) 基于低复杂度匹配函数的策略[24-28]:该类算法的主要思想是采用较低复杂度的匹配误差函数替代传统的均方误差函数,进而降低误差匹配过程的计算量,常用函数包括像素误差分类(pel difference classification,简称PDC)、相异像素数目(different pixel count,简称DPC)、改进的异或函数等.
(5) 基于低比特深度像素的策略[29-34]:这类策略的基本思路是通过某种映射方法将8bit深度的像素变换为低位深的像素,以此来减少运动估计的计算开销,如1bit搜索和2bit搜索等,常与第(4)类策略结合使用.
(6) 基于哈希映射的策略[35,36]:这类算法主要通过哈希函数将待匹配块映射为一个哈希值,从而借助哈希表来提高较大搜索窗口下的块匹配效率.
(7) 基于块分类的策略[1,37]:该种策略的核心思想是按照率失真准则将待匹配块分成不同运动幅度的类,并为不同类别的待匹配块选取恰当的运动估计算法完成预测,从而在保证预测效率的情况下尽量降低计算量.
一方面,尽管众多研究人员对基于平移模型的块匹配运动估计算法进行了上述改进,但仍未从根本上解决运动估计环节计算负载过高的问题.另一方面,块平移模型既无法有效预测由物体旋转、缩放、变形和摄像机运动产生的非刚性复合运动,又不能准确表示具有复杂形状的运动区域,导致在运动物体边缘产生大幅值的预测残差,影响后续的熵编码效率.为此,H.264/AVC(advanced video coding)和H.265/HEVC(high efficiency video coding)等新一代编码标准将早期的正方形宏块改进为对称或非对称的精细矩形块,并进一步采用复杂的分层次可变尺寸块结构、分数像素运动向量、多参考帧和广义B帧等多种优化手段来逼近复杂运动场和运动物体.然而,文献[4]通过实验统计发现,随着块尺寸的减小和运动向量精度的提高,用于编码运动向量、块划分方式的码流开销和各种软/硬件计算开销也逐渐增加,尤其是当矩形块尺寸减小至4×4像素、向量精度达到1/16像素时,软/硬件开销的增加幅度甚至超过了率失真性能的提升幅度.这个结论说明,仅仅依靠块平移模型来实现运动估计愈来愈无法很好地满足高清/超高清视频、面向视频通信的桌面视频和面向虚拟现实应用的全景视频等视频编码的需求[38,39].因此,越来越多的学者认为,研究能有效表示复杂运动场的高阶运动模型及其参数求解策略是帧间运动估计的未来发展方向之一[40-42],对于下一代视频编码效率的大幅提升有重要意义.
本文首先对比分析典型的高阶运动模型的优势和不足,进而介绍弹性运动模型的基本思想.然后,针对弹性运动估计仍然存在的计算量高、收敛不稳定的问题,引进Levenberg-Marquardt方法进行优化求解,并从黑塞矩阵(Hessian matrix)的快速计算和对角矩阵阻尼系数的自适应更新两方面做出改进,提出一种基于改进Levenberg-Marquardt法的视频弹性运动估计算法.实验结果验证了本文算法的有效性.
1 相关工作
鉴于平移模型的不足,研究人员将高阶运动模型引入到运动估计中,利用高阶函数产生 1个或多个扭曲的参考帧,实现更高质量的运动补偿.依据模型显式表现形式的不同,本文将这些运动估计/补偿算法划分为4类.
(1) 基于网格模型的运动估计[43-49]:该类算法主要利用三角形网格或四边形网格来刻画视频图像中的运动物体或内容,能够实现较为可靠的运动/静止区域划分,并可缓解运动补偿帧的块效应,取得更高的主观质量.但是,文献[50]发现,基于网格模型的运动估计对于相邻网格共有节点的控制和对编码率失真的优化较为困难,尚缺少有效的优化方法,而且需要额外传输网格划分方式的同步信息.
(2) 基于多项式模型的运动估计[38,50-56]:这类算法的基本思路是采用4-参数的一元一次缩放变换模型、6-参数的二元一次仿射变换模型、8-参数的二元二次投影变换模型、12-参数的二元二次变换模型及其混合模型产生全局扭曲的参考帧,能够比平移模型更加有效地捕获物体的平移、旋转、拉伸、仿射、透视和景深变化等丰富的运动形式.但是,随着模型参数的增多,其搜索复杂度明显提高,并且对局部运动的刻画能力不足.
(3) 基于缩放模型的运动估计[57-59]:考虑到多参数模型的运算复杂度,该类算法简化了基于多项式模型的运动估计,通过在平移模型基础上引进缩放因子来表示物体的拉伸运动和景深变化等全局运动,但却不能描述3D错切和由于摄像机的俯仰而产生的物体旋转以及物体的局部变形运动等.
(4) 基于弹性模型的运动估计[42,60-63]:该类算法采用离散余弦函数、小波基函数或样条函数刻画物体的平移、错切和扭曲运动,既能表示全局和局部运动,又可通过调整模型参数个数来控制运动估计的计算复杂度.文献[60]的实验结果表明,基于弹性模型的运动估计在相同码率下获得了比块平移运动估计高0.7dB的运动补偿峰值信噪比(peak signal-to-noise ratio,简称PSNR);文献[61]的结论显示,弹性运动模型可将H.265的输出码率降低3%~12%,而运动补偿失真仅损失1%;文献[62,63]则通过优化弹性模型的求解方法取得了更加理想的预测效率,其平均PSNR比传统弹性运动估计提高了1.42dB,并且比基于块平移模型的全搜索算法高出1.73dB.
因此,综合各个模型之间的对比和现有研究结论可知,弹性运动模型是一种表示复杂运动场的高效率模型.
目前,关于视频弹性运动估计的研究主要集中在以下两个方面.
(1) 弹性运动模型与视频编码标准的结合方式.文献[42]将弹性运动估计引进到H.264中,依据图像的几何特征,采用不同斜率的线段划分待预测块,获得其三角形或四边形网格表示,从而使弹性模型能够更准确地描述复杂形状的运动区域,更好地适应多样的局部运动.文献[39]将弹性运动估计作为 HEVC的一种可选模式,通过已解码帧计算弹性运动场,再利用该运动场重建弹性变形后的参考帧,进而根据率失真准则在平移模型和弹性模型之间进行自适应的选择.但是,文献[39,42]简单地使用传统的高斯-牛顿法求解弹性运动向量,既未能避免弹性运动估计的高计算量,又无法避免搜索陷入局部最优,这会从根本上影响弹性运动估计的有效性和实用性.
(2) 弹性运动向量的优化求解.文献[64]提出了基于1bit深度像素的高斯-牛顿迭代法,文献[65,66]又进一步将其推广到了2bit深度像素的情况下.尽管这3种算法通过避免黑塞矩阵及其逆矩阵的计算并固定迭代步长的方式实现了较快的运动估计速度,但是由于只采用了两个梯度下降方向,并且低位深像素的梯度往往不同于 8 bit深度像素,其预测质量与基于8bit深度像素的弹性运动估计尚存在较大差距.文献[62,63]则通过大量实验发现,弹性运动模型的高斯-牛顿解法对初始迭代点和迭代步长较为敏感,即固定的初始迭代点和迭代步长无法求解出全局最优解,进而采用 2bit深度像素和均匀搜索模板将初始迭代点置于全局最优解的单调区间内,再利用离散余弦变换的低频能量比率和黄金分割法调整迭代步长,使之适应目标函数的线性程度,明显提升了弹性运动估计的计算效率和补偿质量.然而,作为一类牛顿型优化求解方法,文献[62,63]的快速算法在本质上仍不能避免牛顿型方法存在的不足,也就是说,目标函数偏离线性的程度越大,初始迭代点距离全局最优点越远,高斯-牛顿法的收敛速度就越慢,甚至出现远离最优点或不收敛的现象[67].事实上,视频数据以及运动补偿误差的复杂性,匹配误差曲面往往不会呈现给我们期望的理想线性性,文献[62]也已验证了这一点.
因此,对于上述两方面的研究工作来讲,将现有弹性运动模型的高斯-牛顿求解方法做出改进乃至改变是非常必要的,进而在降低其计算量的同时,使之收敛到更优解.这一问题的解决将有助于弹性运动估计走向实用.而从我们所掌握的文献来看,目前尚鲜见相关研究.
2 弹性运动模型以及传统弹性运动估计算法
为了便于下文工作的论述,本节首先介绍弹性运动模型,然后介绍运动向量的典型求解方法.
2.1 弹性运动估计模型简介
视频运动估计的目标是在参考帧的某个搜索窗口内,为当前待预测块I(尺寸为B×B像素)搜索到一个运动向量(矢量),使得I与其最佳匹配块R之间的误差平方和(sum of squared difference)最小,即:
其中,xij和yij分别表示当前块中i行j列像素的x坐标和y坐标;m表示弹性运动向量;w(·)表示弹性运动函数,其定义为
其中,p表示运动矢量的分量数目;φk表示弹性运动模型的基函数.虽然样条函数、仿射函数、小波函数都可作为基函数,但是文献[60]经过对比发现,选取离散余弦函数作为基函数对连续运动场具有较高的表示效率,即:
2.2 弹性运动估计的高斯-牛顿求解方法
为了获得弹性运动向量 m,文献[39,42,60-63]均采用了高斯-牛顿法进行求解,其主要思想是对匹配误差函数(公式(1))进行线性逼近,再通过反复迭代求出极小值.具体地,假设当前迭代点是 m,并令像素(xij,yij)处的预测误差为eij(m)=R(w(xij,m),w(yij,m))-I(xij,yij),则函数eij(m)可用其在m处的1阶泰勒展开式近似表示.
为取得上式的最小值,将其对Δm取导并令导数为0,整理后,则有:
其中,上标T表示向量转置.令
显然,H是一个p×p阶的黑塞矩阵,并且根据求导的链式法则和eij(m)、公式(2)、公式(3)的定义,有:
其中,∂R∂xi′j和∂R∂yi′j分别表示匹配块沿着水平和竖直方向的梯度分量;∂w∂m是一个雅克比矩阵,并且∂w∂mk=∂w∂mp/2+k=φk(i,j),k∈[1,p/2].于是有Δm=H-1b,进而得到更新后的弹性运动向量m:m←m+Δm.
3 基于Levenberg-Marquardt法的弹性运动估计
对于弹性运动估计这类非线性无约束最小二乘问题,主要有两类典型的优化解法:牛顿型方法(如牛顿法和高斯-牛顿法)和负梯度方法(如最速下降法和对角线近似法)[67].理论表明,当初始迭代点距离局部极小点较近时,牛顿法和高斯-牛顿法的收敛速度更快;反之,牛顿法和高斯-牛顿法则收敛较慢,甚至会由于黑塞矩阵奇异或病态导致无法收敛的情形发生[68],而此时最速下降法和对角线近似法的收敛效率更高.故而,弹性运动估计的高斯-牛顿解法对初始搜索点存在一定的敏感性,文献[62,63]的研究也验证了这一结论.在这种情况下,文献[69,70]将对角线近似法与高斯-牛顿法相结合,修正了高斯-牛顿黑塞矩阵,提出了一种 Levenberg-Marquardt(下文简称L-M)黑塞矩阵:
从其定义可见,当δ<<1时,HLM近似为高斯-牛顿黑塞矩阵H;而当δ>>1时,HLM则近似为对角矩阵(仅差1个步长因子1/δ).
在HLM的基础上,本文提出了基于L-M算法的弹性运动估计,其计算步骤如下所示.
Step 1. 输入当前待预测块I和迭代次数T,并将弹性运动向量m初始化为0,令δ←1,迭代次数t←1.
Step 2. 根据弹性运动向量m和弹性运动函数(公式(2)、公式(3))计算I的匹配块R(w(xij,m),w(yij,m)).
Step 3. 计算初始运动补偿误差eij(m)及其平方和D0.
Step 4. 计算匹配块的梯度∇R.
Step 5. 计算雅克比矩阵∂w∂m.
Step 9. 根据公式(11)计算L-M黑塞矩阵HLM.
Step 11. 更新当前块I的匹配块R(w(xij,m),w(yij,m)),并计算它与当前块I的匹配误差平方和Dt.
Step 12. 若Dt>Dt-1,则令δ←δ×λ(λ为对角矩阵阻尼系数的更新因子,传统 L-M 算法一般将其设置为10),转入 Step 9;否则,转入 Step 13.
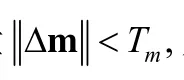
与高斯-牛顿优化算法相比,L-M 算法对于光滑目标函数体现出收敛速度快、稳定性能好等优点.但是,一方面它在每次迭代时均需计算黑塞矩阵及逆矩阵,其渐近时间复杂度达到了max{O(p3),O(p2B2)};另一方面,现有文献往往将对角矩阵阻尼系数的更新因子λ设置成正数,这对于阶数较低的、形式简单的显式目标函数较为有效.但是,视频运动补偿的误差曲面非常复杂,甚至无法用任何一个显式函数表示出来.实验结果表明,λ为正数在某些情况下反而会增大运动补偿误差,而将其设置为负数却更有效.基于上述考虑,下文从黑塞矩阵的快速计算和对角矩阵系数的自适应更新两方面改进L-M算法,进一步提高弹性运动估计/补偿的效率.
4 黑塞矩阵的快速计算方法
由第 2节和第 3节可知,黑塞矩阵的计算与参考块梯度、弹性基函数有关,并且黑塞矩阵本身也具有明显的对称性.为此,本文从两个角度加快黑塞矩阵的计算:(a) 根据2D离散余弦函数矩阵的特点减少基函数的计算量;(b) 利用黑塞矩阵的对称性避免重复计算.
4.1 弹性运动基函数的快速计算
根据公式(4),弹性运动模型共有4种基函数.以B=8为例,图1给出了4种基函数对应的8×8矩阵的数值分布.其中,符号A~H分别代表 cos(π/16)、cos(3π/16)、cos(5π/16)、cos(7π/16)、cos(9π/16)、cos(11π/16)、cos(13π/16)和 cos(15π/16).
从图1可见:① 第1个基函数矩阵只包含元素1;② 第2个基函数矩阵的元素只与纵坐标有关;③ 第3个基函数矩阵的元素只与横坐标有关;④ 第4个基函数矩阵的元素为第2个和第3个基函数矩阵的对应元素之积.故此,基函数矩阵可通过少量计算和大量赋值得到,即:首先,φ1对应的矩阵只需全部赋值为 1;其次,φ2对应的矩阵只需计算一行,其余各行通过赋值得到,转置后再赋值给φ3的各列;最后,将φ2和φ3矩阵的上三角元素对应相乘得到φ4矩阵的上三角元素,而下三角元素可通过转置赋值获得.这样,需要计算的元素个数仅占全部基函数矩阵元素数量的17%.
4.2 高斯-牛顿黑塞矩阵的快速计算
由黑塞矩阵的定义可知,其上三角元素和下三角元素关于主对角线对称,即Ha,b=Hb,a(1≤a≤b≤B).
此外,根据黑塞矩阵的计算过程和第 4.1节的基函数矩阵数值分布特点还可进一步发现高斯-牛顿黑塞矩阵中各元素之间的相等关系,从而降低黑塞矩阵的计算量,下面以H1,4和H2,3为例来分析.由两个元素的定义,有:
同理可得,
而由图1所示的基函数矩阵数值分布可知,φ1和φ4对应元素的乘积与φ2和φ3对应元素的乘积相同,即对于∀i,j∈[1,8],有φ1(i,j)φ4(i,j)=φ2(i,j)φ3(i,j).因此有 H1,4=H2,3.
采用与上述相同的推导过程以及公式(14)的等价关系,就可得到图 2所示的高斯-牛顿黑塞矩阵的数值分布.可见,我们只需计算64个元素中的27个:A~H、a~s,其余的37个元素只需简单赋值即可得到.同时,L-M黑塞矩阵(见公式(11))第2项的对角元素与高斯-牛顿黑塞矩阵的对角元素A~H相同,无需计算.
综上,L-M黑塞矩阵HLM中需要计算的元素个数仅占全部元素数量的37.5%.
5 对角矩阵阻尼系数的自适应更新方法
5.1 λ的取值对弹性运动估计效率的影响
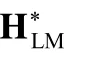
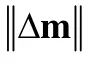
为此,文献[71,72]分别将每次迭代后的目标函数值及其0.01倍作为阻尼系数δ.但当初始迭代点距离全局最优点较远时,文献[71,72]的方法将由于目标函数值过大导致迭代步长很小而无法快速收敛;反之,该方法又会产生过小的δ,使得对角矩阵丧失梯度下降作用.尽管文献[73]进一步采用目标函数值的s-范数(s∈[1,2])来更新δ,能够在一定程度上克服上述不足,但是如何根据迭代点与全局最优点的距离选择合适的s也并不容易,并且不能有效避免目标函数值在迭代后期出现反复振荡.于是,文献[74]提出一种基于对数线性函数的对角矩阵系数更新方法,增强了传统L-M算法的收敛稳定性,而其初始迭代速度却较慢.针对这一不足,文献[75]提出通过迭代向量m之间的内积来计算更新因子λ,加快了初始迭代效率,同时引进对角优势矩阵(diagonally dominant matrix),减少了为使矩阵 HLM正定而反复更新δ所需的尝试次数;文献[76]根据目标函数值的实际下降量与预测下降量之比确定更新因子λ;文献[77]则利用测地线距离来修正迭代步长.然而,这 3种方法需要的计算量均较大,分别需多次判断HLM的正定性、根据泰勒展开式计算匹配误差的预测下降量、计算目标函数的测地线距离,不能满足弹性运动对低运算量的要求.故此,下文提出一种用来自适应更新δ的快速策略.
5.2 基于步长平方商的对角矩阵阻尼系数交替更新
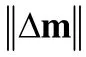
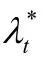
但是,公式(15)给出的自适应因子依然是正数,其目的是通过保证 HLM正定性使迭代求解沿着运动补偿误差曲面的下降方向进行.尽管这是一种稳妥的做法,但文献[77]的研究结论却表明,当迭代点陷入由多个运动补偿误差曲面峰所围的狭长谷底时,保持自适应因子为正数会形成一条锯齿状搜索路径,若适当允许朝着函数值增长的方向迭代则可更快地收敛到更小点.基于这一思路,本文在搜索中借助梯度方向提出一种δ的正、负交替更新策略.直观起见,图 5给出了这一过程的示意图,其中,灰度越浅的区域表示补偿误差越大.可见,当前迭代点处于两峰之间的谷底,其负梯度指向远离全局极小点的方向,且由于距离全局最优解较远,沿高斯-牛顿方向搜索会出现收敛速度慢甚至无法收敛的情况,而此时利用梯度方向与高斯-牛顿方向的矢量和控制迭代却有望将搜索引导向全局最优点.具体地,δ的正、负交替更新方法是
其中,Dt和Dt-1分别表示第t次迭代和第(t-1)次迭代的匹配误差平方和,从而以高斯-牛顿方向HGN为中心,沿着当前搜索方向的对称方向进行搜索(如图 3所示的H*LM和H′*LM),使搜索方向可达整个运动向量空间,提高了算法收敛到全局最优解的概率.
6 采用改进L-M法的弹性运动估计步骤
在第3节算法的基础上,结合第4节和第5节的改进思路,下面给出基于改进L-M法的弹性运动估计步骤.对于每个待预测块I,其运动估计/补偿的详细步骤如下.
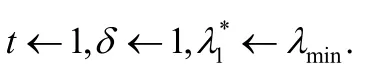
Step 2. 利用整数像素精度的菱形搜索估计平移分量m1和mp/2+1,将其余分量置0,并计算I的初始运动补偿误差eij(m)及其平方和D0.
Step 3. 根据第4.1节计算弹性运动基函数φ1~φp.
Step 4. 计算匹配块的梯度∇R以及雅克比矩阵∂w∂m.
Step 5. 根据第4.2节计算高斯-牛顿黑塞矩阵H.
Step 6. 将H及其主对角线元素、eij(m)、δ代入公式(8)、公式(11),计算向量b和L-M黑塞矩阵HLM.
Step 8. 将运动向量m代入公式(2)和公式(3),建立I的每个像素与其匹配像素的坐标映射,并利用双线性插值计算匹配像素的值,从而得到运动补偿误差eij(m)及其平方和Dt.
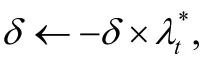
7 实验结果与分析
为了验证本文算法的有效性,以CIF(common intermediate format)、4CIF和高清格式的37个标准视频序列(见表1)的1~90帧为例进行大量实验,并将基于块平移模型的全搜索(full search,简称FS)、基于改进高斯-牛顿法的弹性运动估计[62]、基于菱形搜索(diamond search,简称DS)+传统L-M法的弹性运动估计、基于菱形搜索+对角优势矩阵的L-M法的弹性运动估计[75]和基于改进L-M法的弹性运动估计的预测结果进行比较.

Table 1 Test video sequences’ names and their formats表1 测试视频序列名称及其格式
实验参数设置如下:搜索窗口为33×33像素,块尺寸为16×16像素,λmin=2,λmax=10,Tm=0.0001,T=15(这与文献[60,62]的设置相同);文献[75]的参数与原文相同.运动补偿帧的质量采用PSNR进行评价.
7.1 运动估计/补偿质量的比较
表2给出了各个测试序列的亮度分量采用不同运动估计算法所得到的平均PSNR.
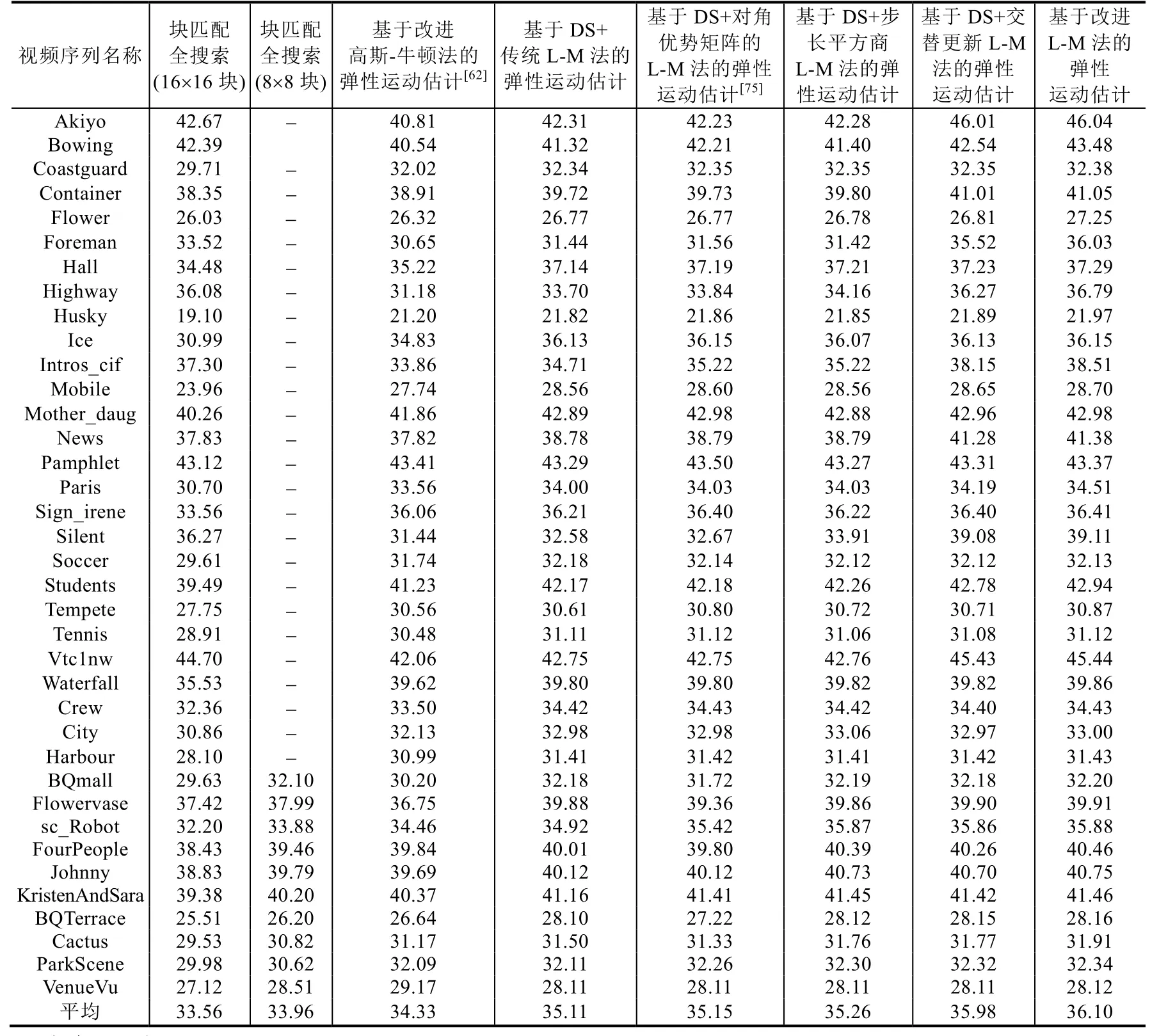
Table 2 Motion-compensated PSNR comparison表2 运动补偿的PSNR比较
由表2可知:
● 尽管 FS是目前编码标准中预测精度最高的运动估计/补偿算法,但是由于运动模型本身的局限,其平均PSNR比本文算法低2.54dB.
● 基于改进高斯-牛顿法的弹性运动估计利用初始迭代点预测和一维线搜索取得了优于 FS的性能(比后者高出0.77dB),但其PSNR却比本文提出的基于菱形搜索+传统L-M法的弹性运动估计低0.79dB,这表明,L-M法比高斯-牛顿法更适用于弹性运动模型的求解.
● 基于菱形搜索+对角优势矩阵的 L-M 法的弹性运动估计利用迭代向量内积更新对角矩阵阻尼系数,其PSNR比基于菱形搜索+传统L-M法的弹性运动估计提高了0.04dB,表明自适应选取阻尼系数有利于获得更高的运动补偿质量.然而,由于文献[75]修改 L-M 黑塞矩阵的方式无法保证其是严格对角占优的,且被修改的对角元素难免不会使迭代过程偏离真实的梯度下降方向,其PSNR较之基于改进L-M法的弹性运动估计低0.95dB,这说明本文的系数自适应交替更新策略可更有效地提高弹性运动估计预测精度.
● 表2第7列和第8列进一步对比了基于步长平方商和基于交替策略(λ=10)的对角矩阵阻尼系数更新方法的性能增益,两者的平均PSNR比基于菱形搜索+传统L-M法的弹性运动估计分别提高了0.15dB和0.87dB.可见,正、负交替更新策略为本文算法贡献了大部分的性能提升.
另外,对于高清视频的运动估计,H.264和HEVC通过缩小块尺寸的方式提高了预测准确率;而且,在相同的块尺寸条件下,块平移模型的运动向量数量仅为弹性模型的 1/4.为此,本文统计了当块尺寸为 8×8像素时,块匹配FS对10个高清视频序列的运动补偿PSNR(结果见表2第3列),虽然它在这10个序列上的平均PSNR比16×16像素的块匹配 FS提高了 1.15dB,但是仍较基于改进 L-M法的弹性运动估计(16×16块)低 1.16dB.可见,即使采用了更精细的块结构,在同等的运动向量开销下,基于块平移模型的全搜索性能仍与本文算法存在一定差距.
需要指出,本文算法在高清VenueVu序列上的PSNR与8×8像素的块匹配FS、基于改进高斯-牛顿法的弹性运动估计存在一定差距.其原因在于:该视频是由计算机生成的动画序列,纹理细腻且存在快速的全局形变,而本文算法在初始搜索时选用的菱形运动估计精度低于后两种算法的全搜索.如果采用与基于改进高斯-牛顿法的弹性运动估计相同的初始搜索,本文算法对VenueVu序列的运动补偿PSNR将达到29.51dB.这表明,本文的对角矩阵自适应更新方法在个别情况下也不能完全克服传统L-M算法对于初始迭代点的敏感性.
图6(a)~图6(d)进一步给出了Akiyo、Foreman、Mobile和Husky序列的PSNR逐帧比较情况.
如图 6所示,这 4个序列的纹理细节和运动复杂度依次增高,且包含摄像机的拉摄、摇摄运动和物体的局部形变.从图中可见,对于具有不同纹理、运动特点的视频序列,基于改进L-M法的弹性运动估计均取得了最高的运动补偿质量.并且,对于快速摇摄、纹理细节复杂的序列(如Mobile、Husky),本文提出的两种算法均明显优于块匹配 FS和基于改进高斯-牛顿法的弹性运动估计;而对于慢速运动或存在局部形变的序列(如 Akiyo、Foreman),基于改进L-M法的弹性运动估计较之块匹配FS亦有稳定提高.
7.2 收敛性和收敛速度比较
收敛性和收敛速度是衡量弹性运动估计效率的重要指标之一.图7所示分别为Husky和Akiyo序列采用基于改进高斯-牛顿法的弹性运动估计、基于改进L-M法的弹性运动估计的前14次迭代结果.可见,首先,前者在纹理和运动较为复杂的序列(如 Husky)上收敛效率较高,反之,却不够理想(如 Akiyo).其次,本文算法最多经过 4次迭代就可达到与最优解相差不到2%的PSNR,而经过1~2次迭代即可取得明显高出块匹配FS的补偿质量.这表明,本文算法的阻尼步长和更新因子符合匹配误差函数的分布特点,能够高效地逼近其最优解.
图8给出了Husky序列第2帧以(48,304)像素为左上角的宏块和Foreman序列第2帧以(0,336)像素为左上角的宏块在第2~15次迭代的误差曲线(第1次迭代的误差较大,为了清晰地展现曲线变化的细节,这里未予绘制),以及在此过程中本文算法的δ值与λ值的变化情况.不难发现,尽管传统 L-M 算法和基于对角优势矩阵的L-M 算法[75]的运动补偿误差均出现了振荡,但是本文算法却能保持稳定的下降趋势.并且,随着算法的收敛,δ与λ也逐渐趋于定值,从而保证了本文的改进 L-M 算法在靠近全局最优解时表现出高斯-牛顿法的快速收敛特性.
7.3 计算复杂度分析
下面对比分析基于块平移模型的全搜索、基于改进高斯-牛顿法的弹性运动估计和基于改进 L-M 法的弹性运动估计处理1个宏块的计算量.设块尺寸为B×B像素,搜索窗口为W×W像素,弹性基函数为p个.
首先,基于块平移模型的全搜索的计算复杂度为O(B2W2).
其次,根据文献[62],基于改进高斯-牛顿法的弹性运动估计的计算复杂度为O(Tp2B2+73B2).
最后,基于改进 L-M 法的弹性运动估计需进行 1次菱形搜索,其复杂度约为块匹配 FS的 6%[6],即O(0.06B2W2);每次迭代需计算对角矩阵阻尼系数、黑塞矩阵、逆矩阵、矩阵乘法、双线性插值和运动补偿误差,结合第4节的快速实现,其计算复杂度分别为O(1)、O(0.375p2B2)、O(p3)、O(pB2)、O(8B2)和O(B2),T次迭代的渐近时间复杂度为O(0.375Tp2B2).
具体地,当B=16,W=33,T=15,p=8时,本文算法的总计算量约为基于块平移模型的全搜索的65%,为基于改进高斯-牛顿法的弹性运动估计的51%.此外,由第7.2节可知,本文算法一般仅需1~2次迭代就能取得高于两者的PSNR,从这个意义上讲,基于改进L-M法的弹性运动估计的计算量约是块匹配FS的9.9%~13.9%,是基于改进高斯-牛顿法的弹性运动估计的7.8%~10.8%.
8 结 论
弹性运动模型是一种表示非刚性复合运动的有效方法,现有工作均采用高斯-牛顿法进行求解,但仍存在迭代计算量高、收敛不稳定的不足.为避免高斯-牛顿黑塞矩阵出现奇异或病态,本文引进L-M优化算法求解弹性运动模型,并进行了两方面的改进:第一,根据黑塞矩阵的数值分布,给出一种快速计算黑塞矩阵的方法,降低了多次迭代所需的计算量;第二,通过理论和实验探讨了L-M对角矩阵阻尼系数的更新因子对弹性运动估计的影响,设计了一种自适应交替更新策略.在此基础上,提出一种基于改进 L-M 法的视频弹性运动估计算法.实验结果验证了算法的有效性.同时,本文算法对于视频处理中相关的无约束最优化问题求解具有一定的参考价值.
另外,本文方法仍存在若干问题可臻完善,如减少逆矩阵的反复计算、快速预测初始迭代点等,我们将在今后的工作中进一步深入研究这些问题的解决思路.

