变量变换回归分析(II)拟合近似呈均匀分布资料的方法——

胡良平

(1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

1 概 述

1.1 如何直观分析散布图的表现

在单个自变量的回归分析中，为了选择到合适的回归分析模型，最简单且最有效的方法是先绘制(X，Y)的散布图。通常可依据散布图中所有散点的分布情况，结合初等函数的表达式及其图象[1]，尝试拟合几种最可能的曲线类型(也包括直线)，并通过拟合优度比较，最终确定一种最合适的曲线回归模型。然而，如图1中散点所呈现的“形态”，确实难以作出合理的判断。所有散点几乎在一个长方形区域内“星罗密布”，说它们近似呈“均匀分布”似乎比较合理。

图1 大气压值(pressure)随年份值(year)变化而变化的散布图

1.2 变量变换的必要性

对于图1中散点的分布情况，若直接拟合直线回归模型似乎是很合理的，但在统计学上又是毫无价值的(因为R2=0.0071)。所以，应采用合理的变量变换方法，使变换后的“新因变量”与“新自变量”之间呈现出较好的相关关系，以便尽可能地反映图1中大多数散点的变化趋势(即具有较高的拟合优度)。由此可知，“变量变换”是成功实现曲线拟合的有效途径。

2 一个取自SAS帮助的数据集

2.1 数据集的名称和数据结构

在SAS帮助“数据库”或“文件夹”中，有一个名为“sashelp.enso”的SAS数据集，其数据含义与结构如表1所示[2]。

表1 澳大利亚港口城市与东部岛屿之间大气压值的变化数据

因篇幅限制，表1中仅列出了该数据集的前5行和最后5行。该数据集中含有3个变量和168个观测(即N=168)。以下SAS程序可以显示出完整的SAS数据集：

proc print data=sashelp.enso noobs;

run;

2.2 用散布图呈现完整资料的变化趋势

以下SAS程序可以呈现图1中的大气压值(pressure)随年份值(year)变化而变化的趋势：

proc transreg data=sashelp.enso;

model identity(pressure)=identity(year);

run;

以上程序输出结果为图1。由图1可知，除少数点外，绝大多数点几乎是随机地分布在一个长方形区域内，近似呈“均匀分布”。此长方形与X轴不完全平行，略呈一个微小的倾斜角。图1中的实线是基于最小二乘原理拟合出来的一条直线，按常规的统计学理念，这种表现的散布图提示分析者，对此资料拟合直线回归模型是无可非议的。然而，其R2仅为0.0071，说明用年份值去预测大气压值是非常不准确的。

2.3 统计分析的任务

针对图1中散点的分布或变化趋势，可否找到一个较为合适的统计模型，使R2>0.6，即用年份值(year)预测大气压值(pressure)的预测结果具有一定程度的准确性。

3 基于TRANSREG过程中各种样条变换后建模[2-3]

3.1 基于B-样条变换(spline)后建模

3.1.1 基本概念与做法

在SAS中，实现B-样条变换的关键词为“spline(自变量名)”。在运用SAS的TRANSREG过程时，可以对自变量year进行“B-样条变换”，变换后的结果记为Tyear。再构建因变量pressure关于新自变量Tyear的回归模型。所谓“B-样条变换”，实际上就是拟合因变量关于自变量的多项式曲线回归模型，一次就是直线回归模型、二次就是抛物线回归模型、三次就是三次多项式回归模型，以此类推。通常，拟合三次多项式回归模型。

问题在于：是在自变量的整个取值区间内拟合一个样条函数曲线模型，还是将区间划分成多个子区间，分别在各子区间上各拟合一个样条函数曲线模型，即“分段拟合”。若在“nkonts=”之后写一个“k(k≥0)”，就是将自变量的整个区间划分成“k+1”个子区间。“nkonts”代表“节点数”或“断点数”，“nkonts=k”代表节点数为“k”。显然，随着k值增加，分段数目也在增加，在各个很短的子区间上的“多项式曲线”能更好地拟合该子区间上的散点，因而拟合的效果就会提升，直到曲线回归模型完全拟合给定的实际资料。下面给出“nkonts=0”“nkonts=5”“nkonts=10”等情形下的拟合结果。

3.1.2 SAS输出结果及解释

基于B-样条变换且节点数k取不同数值时对应的拟合效果(以R2来度量)。见表2。

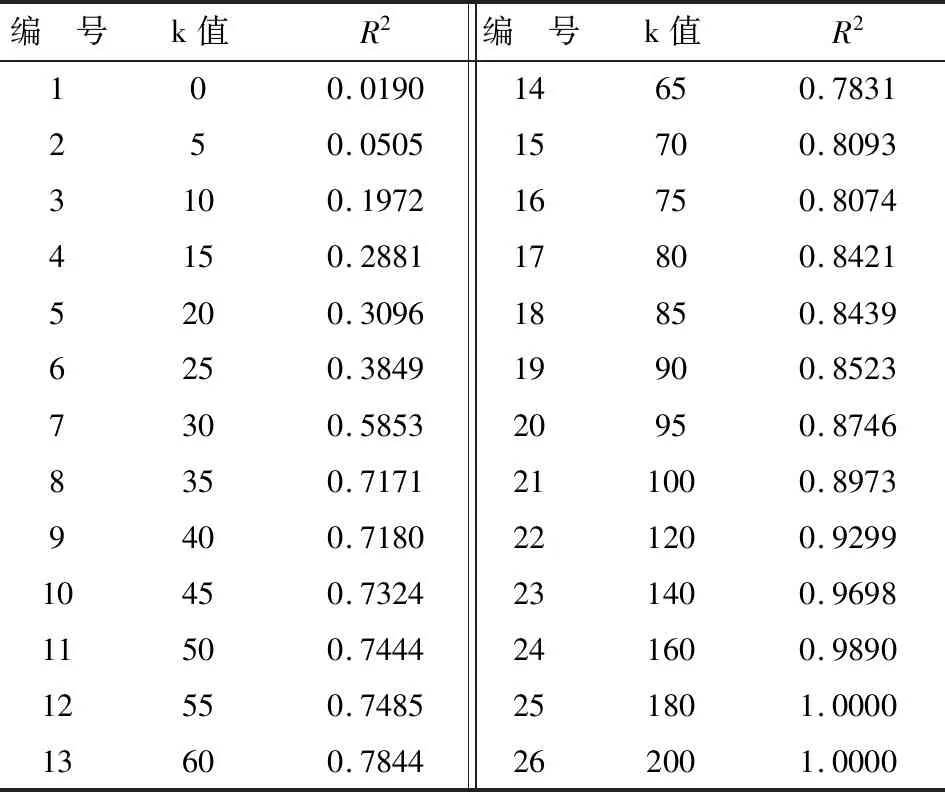
表2 基于B-样条变换且节点数k取不同数值时对应的R2值

由表2可知，除了k=65和k=75两行外，其他各行的R2都随着k值增大而增大。其根本原因在前面已述及，此处不再赘述。按R2>0.6且回归模型尽可能精简的要求，k=35即可。若进一步尝试，发现k=31时，R2=0.6751，此时拟合的图形见图2。

图2 k=31时B-样条变换对资料的拟合效果图示

3.1.3 “nkonts=k”所对应的SAS程序

注意：“k”必须取一个具体数值，下面给出k=31时对应的SAS程序。

proc transreg data=sashelp.enso outtest=aaa ss2 coefficients test;

model identity(pressure)=spline(year/nknots=31);

output out=bbb predicted residuals;

run;

3.2 基于B-样条基函数变换(bspline)后建模

3.2.1 基本概念与做法

在SAS中，实现B-样条基函数变换的关键词为“bspline(自变量名)”。与前面的“B-样条变换”一样，也可以通过给“nkonts=k”中的“k”赋一个具体值，来获得拟合效果不同的拟合结果。而且，两者的计算结果完全相同。它们之间的区别仅仅在于：使用“bspline(自变量名)”时，可以输出“B-样条基函数”的计算结果，而使用“spline(自变量名)”时，无法输出“B-样条基函数”的计算结果。

3.2.2 SAS输出结果及解释

基于B-样条基函数变换且节点数k取不同数值时对应的拟合效果(以R2来度量)，与表2完全相同，此处从略。下面分别将k=0、k=1和k=2时对应的“B-样条基函数”的计算结果呈现出来。

第一种情形：k=0时对应的“B-样条基函数”的计算结果见图3。

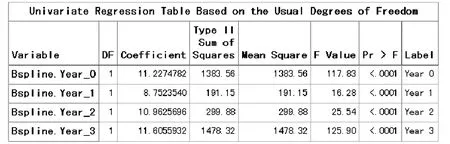
图3 k=0时对应的“B-样条基函数”的计算结果

图3中的结果表明：在自变量year的整个取值区间内，拟合了一个“三次多项式曲线回归模型”，其表达式见式(1)。

(1)

第二种情形：k=1时对应的“B-样条基函数”的计算结果见图4。

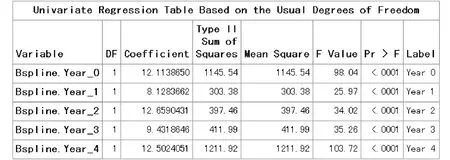
图4 k=1时对应的“B-样条基函数”的计算结果

图4中的结果表明：在前面式(1)基础上，又增加了一项“t4”及其系数估计值。但前面各项的系数估计值也作了相应的调整。

第三种情形：k=2时对应的“B-样条基函数”的计算结果见图5。

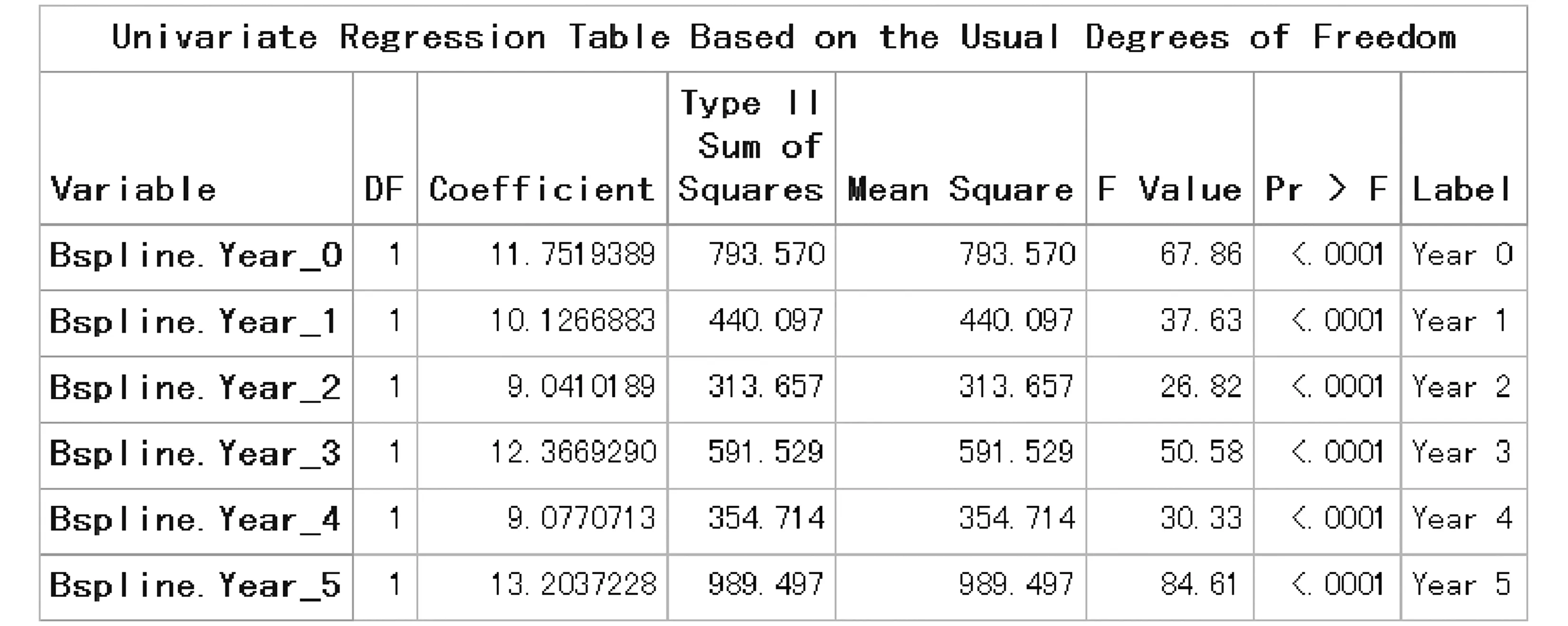
图5 k=2时对应的“B-样条基函数”的计算结果

图5中的结果表明，在前面的基础上，又增加了一项“t5”及其系数估计值。但前面各项的系数估计值也作了相应的调整。

由此可知，自变量year经过变量变换后的变量数目随着k值的增加而增加，其具体个数为(4+k)。即k=0时，有4个；k=1时，有5个；而k=2时，有6个。值得注意的是，变换后的变量的下角标从“0”开始。

3.2.3 “nkonts=k”所对应的SAS程序

注意：“k”必须取一个具体数值，下面给出k=5时对应的SAS程序。

proc transreg data=sashelp.enso outtest=aaa ss2 coefficients test;

model identity(pressure)=bspline(year/nknots=5);

output out=bbb predicted residuals;

run;

3.3 基于单调B-样条变换后建模

3.3.1 基本概念与做法

在SAS中，实现单调B-样条变换的关键词为“mspline(自变量名)”。与前面的“B-样条变换”一样，也可以通过给“nkonts=k”中的“k”赋一个具体值，来获得拟合效果不同的拟合结果。

3.3.2 SAS输出结果及解释

基于单调B-样条变换且节点数k取不同数值时对应的拟合效果(以R2来度量)。见表3。

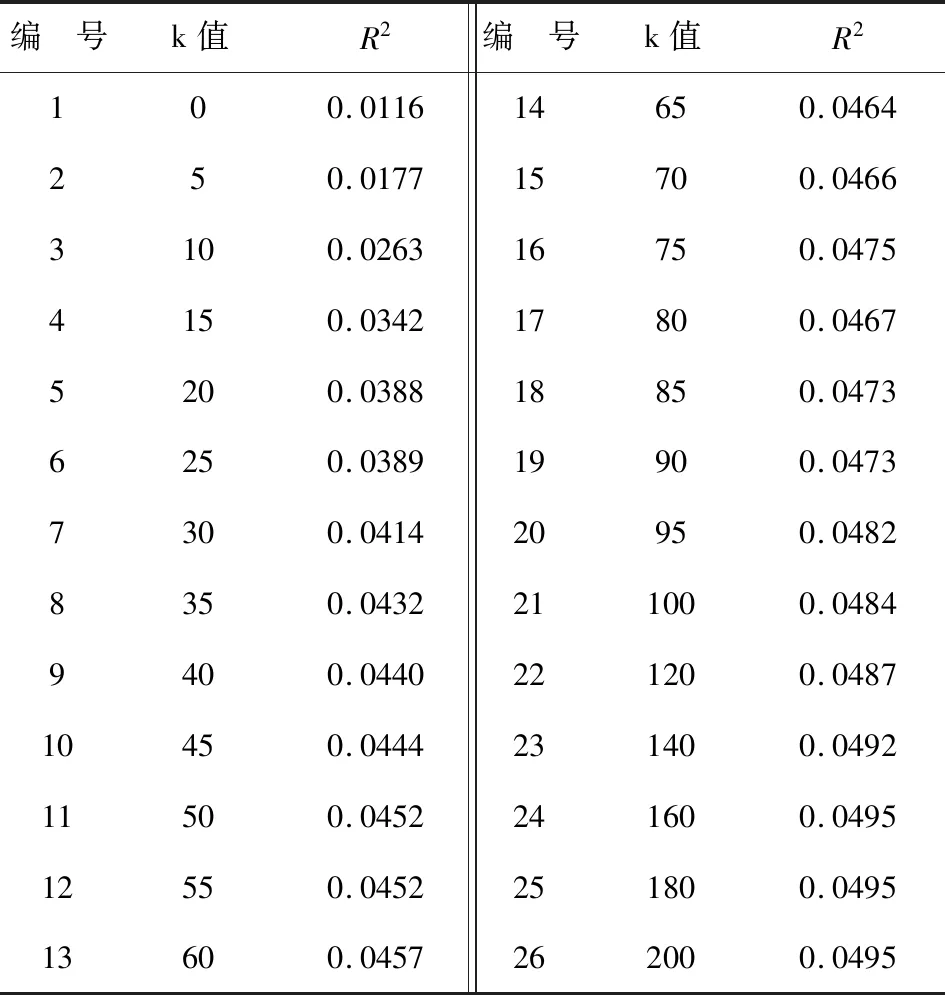
表3 基于单调B-样条变换且节点数k取不同数值时对应的R2值

表3与表2相比，随着回归模型越来越复杂，表3中的R2值增加十分缓慢，且R2最大值均未超过0.05。

3.3.3 “nkonts=k”所对应的SAS程序

注意：“k”必须取一个具体数值，下面给出k=160时对应的SAS程序。

proc transreg data=sashelp.enso outtest=aaa ss2 coefficients test;

model identity(pressure)=mspline(year/nknots=160);

output out=bbb predicted residuals;

run;

3.4 基于非迭代惩罚B-样条变换(pbspline)后建模

3.4.1 基本概念与做法

在SAS中，实现非迭代惩罚B-样条变换的关键词为“pbspline(自变量名)”。与前面的“B-样条变换”一样，也可以通过给“nkonts=k”中的“k”赋一个具体值，来获得拟合效果不同的拟合结果。

3.4.2 SAS输出结果及解释

基于非迭代惩罚B-样条变换且节点数k取不同数值时对应的拟合效果(以R2来度量)。见表4。

表4 基于非迭代惩罚B-样条变换且节点数k取不同数值时对应的R2值

观察表4，很难总结出其中规律，当k=0、k=65、k≥100时，都能获得较大的R2值。事实上，在使用pbspline变换时，涉及到一个关键的“光滑参数lambda”。当此参数取不同数值时，回归模型对资料的拟合效果是不同的。有多种评价指标用来衡量回归模型对资料的拟合优度，其中，SBC统计量是经常被选用的。SBC取值最小时，对应的“lambda值”是最合适的光滑参数。此时，对应的R2将取极大值。

3.4.3 寻找使SBC取得极小值时所对应的SAS程序

运行下面的一段SAS程序，可以找到使SBC=398.9为极小值，此时，lambda=1.14。

proc transreg data=sashelp.enso;

model identity(pressure) = pbspline(year/sbc lambda=.1 to 100.1 by 0.01);

run;

运行下面的一段SAS程序，可以找到使SBC=435.7为极小值，此时，lambda=1801.1。

proc transreg data=sashelp.enso;

model identity(pressure) = pbspline(year/sbc lambda=100.1 to 10000.1 by 0.01);

run;

由于在lambda的整个取值范围内，SBC取最小值时，回归模型对资料的拟合优度最好，故应取lambda=1.14。使用下面的SAS程序，可以快速获得最大的R2=0.6999。

proc transreg data=sashelp.enso outtest=aaa ss2 coefficients test;

model identity(pressure)=pbspline(year/sbc lambda=1.14);

output out=bbb predicted residuals;

run;

3.5 基于迭代光滑样条变换(sspline)后建模

3.5.1 基本概念与做法

在SAS中，实现迭代光滑样条变换的关键词为“sspline(自变量名)”。与前面的“B-样条变换”不一样，它不能通过给“nkonts=k”中的“k”赋一个具体值，来获得拟合效果不同的拟合结果。但它引入了一个“光滑参数smooth (简写为sm)”，通过调整sm的数值，可以获得拟合效果不同的拟合结果。sm的取值从0开始，其取值区间为[0，100]，即可取此区间内任何一个实数，也包括区间的两个端点。数值越小，表明光滑程度越差，当sm=0时，就是将所有相邻的两点用折线连起来，此时，为完全拟合(也称为“过拟合”)；当sm=100时，就是用一条直线来拟合该资料，拟合的效果最差。因此，可以依据R2的大小，尝试寻找合适的sm数值。

3.5.2 SAS输出结果及解释

经尝试，当sm=22.2时，R2=0.6039；当sm=22.3时，R2=0.6008；当sm=22.4时，R2=0.5976；当sm=22.5时，R2=0.5944。通过进一步尝试，发现当sm=22.32时，R2=0.6001，刚好满足R2>0.6的基本要求。

3.5.3寻找使R2略大于0.6时的sm数值所对应的SAS程序

proc transreg data=sashelp.enso outtest=aaa ss2 coefficients test;

model identity(pressure)=sspline(year/sm=22.32);

output out=bbb predicted residuals;

run;

3.6 基于非迭代光滑样条变换(smooth)后建模

3.6.1 基本概念与做法

在SAS中，实现非迭代光滑样条变换的关键词为“smooth(自变量名)”。与前面的“迭代光滑样条变换”一样，引入了一个“光滑参数smooth(简写成sm=)”，通过调整sm的数值，可以获得拟合效果不同的拟合结果。

3.6.2 SAS输出结果及解释

经尝试，当sm=20.8时，R2=0.6048；当sm=20.9时，R2=0.6018；当sm=21.0时，R2=0.5989；当sm=21.1时，R2=0.5959。通过进一步尝试，发现当sm=20.96时，R2=0.6001，刚好满足R2>0.6的基本要求。

3.6.3寻找使R2略大于0.6时的sm数值所对应的SAS程序

proc transreg data=sashelp.enso outtest=aaa ss2 coefficients test;

model identity(pressure)=smooth(year/sm=20.96);

output out=bbb predicted residuals;

run;

4 讨论与小结

本文图1中的全部散点几乎呈“均匀分布”状态，常规的直线回归模型没有任何使用价值。然而，在SAS/STAT模块中的“TRANSREG过程”收录了很多种类的变量变换方法。本文采用了其中的一大类方法，即“样条变换方法”。从思路和算法上又给出了六个彼此稍有区别的具体方法，它们各具优点和缺点。根据分析者的目的不同，可以考虑选用不同的方法来拟合资料。

本文介绍的六种样条变换方法主要作用是曲线拟合，在自变量的取值范围内找到合适的曲线回归模型，即尽可能高的拟合优度(如本文期望R2>0.6)且尽可能精简的回归模型(可以回归模型误差项的自由度“DF误差”来反映，其数值越大越好，它标志着回归模型中被估计的参数数目少，即回归模型较为精简)。

B-样条变换和B-样条基函数变换：节点数为31时，R2=0.6751，DF误差=133。

单调B-样条变换：拟合效果极差。

非迭代惩罚B-样条变换：Lambda=1.14时，R2=0.6999,DF误差=131.28。

迭代光滑样条变换：Sm=22.32时，R2=0.6001，DF误差=138.34。

非迭代光滑样条变换：Sm=20.96时，R2=0.6001，DF误差=137.09。

由于以上方法所依赖的“调节参数”不同，因此，结果尚缺乏可比性。但可将R2值定为0.6999，计算出除“单调B-样条变换”之外的其他几种情况下的结果：

B-样条变换和B-样条基函数变换：节点数为34时，R2=0.6974，DF误差=130；节点数为35时，R2=0.7171，DF误差=129。

非迭代惩罚B-样条变换：Lambda=1.14时，R2=0.6999,DF误差=131.28。

迭代光滑样条变换：Sm=18.4时，R2=0.6998，DF误差=131.34。

非迭代光滑样条变换：Sm=16.88时，R2=0.6999，DF误差=129.18。

综上所述，“非迭代惩罚B-样条变换”与“迭代光滑样条变换”的拟合效果基本相同，是以上六种方法中最好的曲线回归建模方法。