非线性幂变换Gammachirp滤波器的鲁棒语音特征提取*

李 聪，葛洪伟+

1.江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122

2.江南大学 物联网工程学院，江苏 无锡 214122

1 引言

语音识别相关系统在其最基本的层次上，是从各种领域和学科研究得到的不同方法的集合体，其中包括信号处理、模式识别和语音语言学等多种学科，这些学科方法中的每一种都要将语音信号波形转化为某种类型的参数表示，这也就是所谓的语音特征提取。特征提取是语音信号处理中最基本也是最重要的一个过程，一种好的特征提取算法能够准确地提取到符合人耳听觉特性的音频特征，并且能够避免由于日常噪声环境所带来的不利影响。

最为经典的语音特征提取方案是以Mel滤波器[1]作为听觉滤波器的梅尔频率倒谱系数（Mel-scale frequency cepstral coefficients，MFCC）[2-3]。Mel滤波器由一组不同频率的三角滤波器组成，模拟了人耳听觉频率的非线性特征，是使用最广泛的听觉滤波器，但是由于其对人耳听觉的研究并不完全，在提取过程中忽略了部分能量信息，因此在噪声环境下会表现出一定的缺陷。为了弥补梅尔滤波器的不足，相关学者在充分研究人耳耳蜗听觉特性后提出了Gammatone滤波器[4-5]，一定程度上减小了噪声对特征提取的影响。Irino等人在Gammatone滤波器基础之上，提出了符合耳蜗基底膜对于频率响应是非线性特性的Gammachirp滤波器[6-8]。该滤波器作为目前较为理想的听觉滤波器，继承了Gammatone滤波器的优点，并弥补了其在非对称性上的不足问题。

归一化功率倒谱系数（power-normalized cepstral coefficients，PNCC）[9]是基于Gammatone滤波器组提出的语音特征，其中融合了幂函数变换、噪声抑制等多种技术，该特征能够有效提升噪声环境下的语音识别和说话人识别性能。虽然该特征有着良好的抗噪性能，但其中的噪声抑制过程计算量过大，复杂度过高，并不适用于实时的语音信号处理系统和小容量语音识别系统。本文结合PNCC的技术基础，提出了一种低系统开销的鲁棒语音特征提取算法——非线性幂函数变换伽马啁啾频率倒谱系数（nonlinear power-function Gammachirp frequency cepstral coefficients，NPGFCC）。该语音特征采用了归一化压缩Gammachirp滤波器进行滤波操作，并在提取过程中，对特征参数进行了分段非线性幂函数变换处理，避免提取过程中出现的能量幅值波动较大的问题，在噪声环境下能够有更好的识别性能。

2 压缩归一化Gammachirp滤波器

Gammachirp滤波器是一种符合人耳听觉特性的非线性滤波器，其时域表达式为：

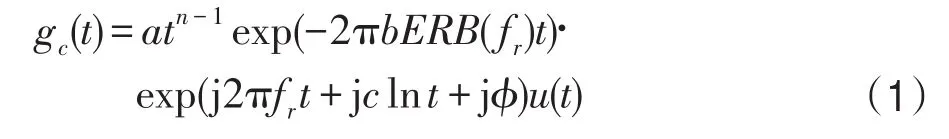
式中，a为幅值；滤波器阶数n和参数b负责调整伽马函数的分布，本文的n和b分别取值4和1.109；fr为滤波器的中心频率；ϕ为初始相位，一般取ϕ=0;c为啁啾因子，其取值范围一般为[-3,3]，c作为Gammachirp滤波器的频率调制参数，使其区别于Gamma-tone滤波器，当c=0时，Gammachirp滤波器也就退化为了Gammatone滤波器。本文中啁啾因子c取值为c=2。

ERB(fr)是频率为fr时滤波器的等价矩形带宽，其计算公式为：

原始Gammachirp滤波器对频率的响应权值分配是平均的，但信号低频部分的频域宽度较高频部分明显窄小，这就造成了响应过程中对处于不同频率信号处理的不均衡问题。针对原始Gammachirp滤波器组高低频权值平均分配的现象，本文算法通过压缩归一化处理方式对滤波器组进行了改进。这样增加了每一个滤波器的频率宽度，并且相应提升了滤波器组低频部分的权重，使得整个特征参数具有更好的抗噪性能，以达到更好的识别效率。以下是Gammachirp滤波器压缩归一化的过程[6]：

其中，GC(i,k)是滤波器组中第k个滤波器在第i个频率处的响应幅值，iFFT为傅里叶变换长度。

如图1和图2所示的分别是改进前原始的32维Gammachirp滤波器组频率响应和压缩归一化后的滤波器组频率响应。通过图像可以看出，经过压缩归一化优化过程后，滤波器的响应曲线在不同频率上分别对应不同的响应幅值，能够更好地表征语音信号所传递的信息。

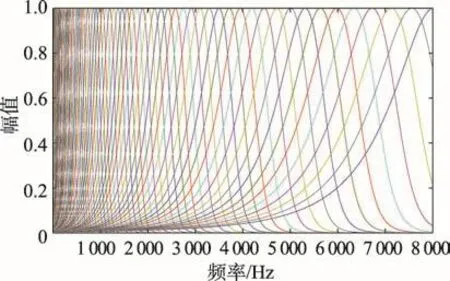
Fig.1 Frequency response of original Gammachirp filter bank图1 原始Gammachirp滤波器组频率响应

Fig.2 Frequency response of compressed and normalized Gammachirp filter bank图2 压缩归一化Gammachirp滤波器组频率响应

3 分段非线性幂函数变换

为模拟人耳听觉模型处理信号的非线性，对每个滤波器的输出做非线性幂函数变换，得到一组能量谱。

非线性幂函数变换是对得到的语音响应系数以幂函数的方式处理[10]。之所以采取这种变换方式，是由于幂函数的输出值并不严格依赖于它的输入值幅度，因此可以很好地模拟各个音强段的特性，有利于改善语音识别的抗噪性能。诸如MFCC等特征提取过程中是利用对数函数对能量幅值进行变换，这其中存在着一定的不足：当输入的能量较低时，经过对数变换后，输入能量的微小的幅值变化便会导致输出能量的较大波动，特别是在输入的能量接近零时，这种能量的输入输出之间巨大的差异就表现得更加明显。因此对数变换的最终结果可能是降低了特征提取后续的识别效率，而本文采用的非线性幂函数变换就很好地弥补了这一缺陷。因此，与其他特征提取中使用的对数函数不同，这里用非线性幂函数对滤波结果进行变换。变换公式为：

其中，Gm是语音信号经过滤波后的响应幅值，Gc是幂函数变换后的响应幅值。这里的指数α取值是大于0且小于1的数。若α的取值较大，也就是接近于1时，幂变换后的特征值不能很好地突出幅值的变化，对识别率的提升效果不明显；若α的取值过小，则会使得原始特征值变化幅度太大，使数据值都趋近于1，脱离了原始数据的分布情况，也不能充分地发挥其作用。在PNCC特征提取过程中，α的取值为固定值，但由于语音特征系数各个分量对识别率的影响有所不同，识别过程中，高阶特征分量相对于低阶特征分量来说，受到的噪声干扰影响较小，具有较强的鲁棒性。

为了使语音特征参数更符合耳蜗听觉特性，提升系统的抗噪鲁棒性，本文提出了对每个滤波器的输出进行分段式指数变换，针对不同频率部分的滤波器响应系数，令α取不同的值进行非线性幂函数变换。这样一来，在降低鲁棒性较差的低阶分量值的同时，又将数值较小的中高阶特征分量值进行了提升[11]，因此能够在抗噪能力方面提供更佳的性能。

本文采用的Gammachirp滤波器组的频率响应范围为0～8 000 Hz，针对这一频率范围，将每1 000 Hz的频率分为一段，对每一频率段分别指定相应的一组幂函数变换指数，全部频率范围共分为9段。根据频率值f的不同，幂函数取值及分段方式如式（5）所示。

4 NPGFCC特征

大多数的语音特征针对安静环境能够有较好的效果，但在复杂的噪声环境下，这类算法普遍存在抗噪性能不佳的问题。为了满足现实应用环境的需要，本文通过对人耳听觉特性的研究来寻求抗噪性能较好的语音特征参数，提出了NPGFCC特征提取算法。该特征基于抗噪性能较好的压缩归一化Gammachirp滤波器，并通过结合和利用分段式非线性幂函数变换、RASTA（relative spectral）滤波、均值方差归一化和时间序列滤波等技术方法，进一步提高了语音特征的抗噪鲁棒性。

NPGFCC特征提取过程如下：

（1）信号预处理。对输入的语音信号x(n)进行预加重处理，经过预加重后的语音信号为：

其中，μ为预加重系数，一般取0.92～0.98之间，这里取μ=0.97。

（2）RASTA滤波处理。相对谱RASTA滤波处理技术是信号处理领域中为了抑制波形中变化缓慢的部分而提出的。该处理方法是利用低频带通滤波器来补偿环境和声道的动态作用，对抑制卷积噪声有较好的效果，因此该技术广泛地应用于信号的信道噪声处理中。本文使用的低频带通滤波器频率响应H(Z)可以表示为如下的形式[2]：

式中，参数G取值为0.1，N取值为5，ρ取值为0.98，Z是输入的语音信号。

通过RASTA处理后得到滤波后的信号y′(n)。

（3）语音信号分帧、加窗。由于语音信号具有短时平稳性，可将信号分为短时的语音帧来方便进行后续操作，并且为了减少语音帧的边缘效应使之平滑过渡，需对分帧后的语音帧进行加窗处理。本文选用的窗口为汉明窗，得到加窗后的语音信号S(n)。

（4）短时傅里叶变换。对加窗后的时域语音帧片段进行快速傅里叶变换（fastFouriertransform，FFT），将其由时域变换到频域，得到每一帧语音信号的快速傅里叶变换后的幅度谱Y(t,i)。

（5）归一化压缩Gammachirp滤波器滤波。具体流程是将上一步变换得到语音幅度谱，通过k阶压缩归一化Gammachirp滤波组进行滤波处理，也就是将每一帧语音信号的功率谱Y(t,i)分别与Gammachirp滤波器组内每一通道的滤波器加权求和，得到语音信号在不同频率分量上的响应Gm(t,k)，它表示第t帧语音信号在第k个滤波器上的响应系数。

本文采用64组不同中心频率的Gammachirp滤波器构成音频滤波器组，因此k的取值为1～64。

（6）分段非线性幂函数变换，根据频率值确定幂函数变换系数α，根据公式进行变换。

（7）离散余弦变换（DCT）。为了减少特征向量的相关性，降低特征矢量的维度，将每一帧语音在Gammachirp滤波器组的响应输出进行离散余弦变换去除其参数间的相关性。本文取DCT变换后的前32维特征进行后续处理，DCT变换[5-6]的过程：

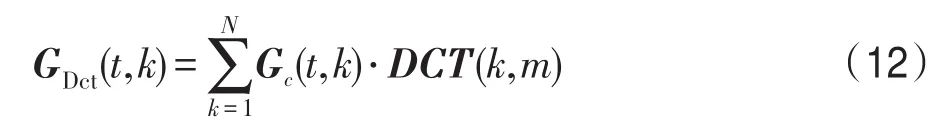
其中，Gc(t,k)代表第t帧语音在第k阶滤波器上的响应输出，GDct(t,k)表示经过离散余弦变换后第t帧语音的特征矢量。DCT(k,m)表示N维离散余弦变换矩阵中第k行m列的值，它的定义是：

（8）倒谱均值方差归一化[12]。通过对倒谱特征进行均值方差归一化过程能够一定程度上消除信道对语音特征的影响。倒谱均值归一化过程是：

倒谱方差归一化过程是：

（9）时间序列滤波[13]。为了降低基音频率对声道特性的影响，对得到的语音特征采用一种平滑滤波的方式来减小基音频率的影响。选取窗口大小为W=5的滑动滤波器对得到的语音特征进行滤波，得出消除基音频率影响后的32维NPGFCC语音特征。

如图3所示是整个NPGFCC语音特征的提取流程。

Fig.3 NPGFCC feature extraction process图3 NPGFCC特征提取流程

5 决策融合i-vector识别模型

目前较为常用的说话人识别模型有高斯混合模型-通用背景模型（Gaussian mixture model-universal background model，GMM-UBM）[14-15]和结合概率线性判别分析（probabilistic linear discriminant analysis，PLDA）的辨识向量（identity-vector，i-vector）[16-18]模型。

单纯的以某一种模型作为说话人识别系统都不免会存在一定误差，为了提升系统的识别精度，本文以i-vector+PLDA作为说话人识别模型，且对其进行了改进，提出了融合决策i-vector说话人识别模型。与i-vector+PLDA模型不同的是，融合决策i-vector说话人识别模型是在决策环节中融合了GMM-UBM似然概率和i-vector的相似度度量，通过将i-vector的相似度度量、PLDA相似度得分和GMM-UBM最大似然概率得分进行归一化加权，最终确定说话人身份。这样一定程度上减少了识别误差，在不增加系统计算复杂度的前提下提升了整体的识别准确性。

将本文所提的鲁棒性NPGFCC特征提取算法用在融合决策i-vector识别模型中，来提高识别系统的整体性能。融合决策i-vector说话人识别模型的识别流程为：

（1）为每一组说话人的训练语音提取NPGFCC特征矢量。

（2）通过对矢量进行训练得到通用背景模型UBM。

（4）根据语音特征，计算说话人对应的Baum-Welch统计量，进而训练得到全变量空间矩阵T。

（5）由T矩阵和前面得到的UBM模型，计算得出每段语句的i-vector矢量。

（6）将所得i-vector矢量进行训练得到高斯PLDA模型。

（7）对需要识别的语音进行特征提取，通过UBM自适应得到GMM，利用全变量空间矩阵T得出其超均值矢量，并提取i-vector。

（8）将训练说话人语音和测试语音间的i-vector矢量通过余弦距离计算其相似度，同时由PLDA模型对矢量间进行打分，并将测试语音特征和训练说话人的GMM模型经最大似然计算得出概率值，通过以上三者的得分值分别归一化处理后进行加权计算，得出融合分值作为最后的决策分，得分最大的说话人作为结果输出。

如图4所示为融合决策i-vector说话人识别模型的整体流程。

6 实验与分析

本实验通过利用TIMIT语音库进行文本无关说话人识别实验。选用其中共100人的音频数据，包括50名男性和50名女性，每人10段发音数据，每段数据长约为3～5 s，信号采样频率为16 kHz。选取每人语音数据中的5段用作训练样本，另5段语音作为测试数据，并对测试语音分别混合不同强度的噪声，共计500条测试样本。实验中的噪声数据来自NoiseX-92数据库，从中选择了Babble噪声、Cafe噪声、Factory噪声以及利用该数据库多种噪声混合而成的Mixed噪声。高斯混合模型的混合度设为32，语音帧长和帧移分别为20 ms和10 ms。信噪比SNR分别取-5 dB、0 dB、5 dB、10 dB、15 dB、20 dB。

Fig.4 Process of imporved i-vector speaker recognition system图4 融合决策i-vector说话人识别系统流程

为了证明算法的有效性，在相同的实验条件下，分别选取了39维的差分MFCC特征、基于Gammatone滤波器组的26维GFCC（Gammatone frequency cepstral coefficients）特征[12]和26维的PNCC特征进行对比实验。

首先验证了本文NPGFCC算法在计算复杂度方面的优势，通过对比不同特征提取算法提取相同500段语音特征所用时间，得到如表1所示的各算法在相同实验环境下的平均用时对比表。

Table 1 Time used by different algorithms表1 不同算法所用时间对比

其次利用本文提出的融合决策i-vector模型，得出不同算法在无噪和有噪环境下的平均识别准确率，如表2和表3所示。

Table 2 Recognition rate of different algorithms in noise-free state表2 算法在无噪声状态下平均识别率

Table 3 Recognition rate in different noisy cases表3 不同噪声环境下识别率

另一方面，为了对比本文提出的融合决策i-vector模型较单一决策模型的优势，使用相同的实验数据，在Babble噪声下利用PNCC和NPGFCC特征分别在GMM-UBM、i-vector、PLDA和决策融合模型下进行了实验对比，得出了如表4所示各个模型下说话人平均识别准确率数据。

通过表1的实验结果可以看出，在运算时间方面，NPGFCC和MFCC、GFCC特征同属一个数量级，都在可接受范围之内。而PNCC算法中，由于要进行噪声估计等过程，对噪声的能量进行估计并通过噪声信息对语音进行滤波处理，因此对系统开销较大，时间复杂度较高，不适用在小容量实时语音处理系统中。本文提出的NPGFCC特征未使用噪声估计这一过程，而是通过利用抗噪滤波器和分段幂函数变换等方式对噪声进行抑制，能够在保证较低时间消耗的前提下提升识别准确率。

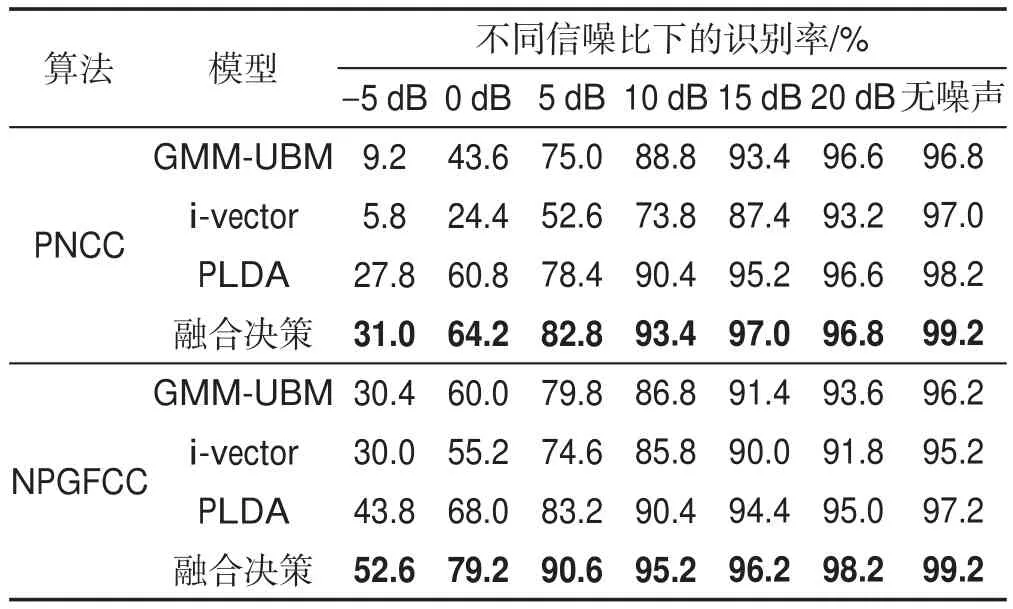
Table 4 Recognition rate in different recognition models表4 不同识别模型下识别率

表2给出的结果是四种算法在未添加噪声的纯净语音状态下的平均识别准确率。实验结果显示，除GFCC特征外，这几种特征算法都达到了较高的识别水准。其中MFCC特征给出了近乎全部识别正确的结果，说明了在无噪声的纯净环境下，MFCC特征有其良好的性能。同时PNCC和NPGFCC也都表现出较高的识别水平，两者识别准确率均达到99.2%，证明了本文算法在纯净语音状态下同样有着较优异的识别能力。

由表3的实验数据可以得出，噪声对识别率影响最大的是MFCC特征，其识别准确率随着信噪比的不断降低出现了急剧的下降，说明了该特征对噪声的异常敏感性。相比之下，GFCC特征较MFCC有一定的改善，主要体现在较低信噪比的时候其识别准确率较MFCC有大幅度的提升。PNCC和NPGFCC特征整体表现相当，且相比MFCC和GFCC，这两种特征表现出了良好的抗噪性能。整体来看，NPGFCC特征的鲁棒性是这些算法中表现最佳的，尤其是在低信噪比情况下，NPGFCC特征算法的优势就更为明显，且在噪声影响较小的时候，算法依然有着很高的识别准确率。与此同时，在不同的噪声环境以及不同信噪比下，本文算法都得出了较理想和稳定的结果，表明了NPGFCC特征在抗噪能力上的有效性和鲁棒性。

表4给出的是PNCC特征和NPGFCC特征分别在GMM-UBM模型、i-vector模型、i-vector+PLDA模型和融合决策i-vector模型下的平均识别准确率对比。从结果分析，结合PLDA的i-vector模型整体识别率要稍好于GMM-UBM和i-vector模型，表明了ivector+PLDA作为目前主流的说话人识别模型在该领域的优势。相比之下，本文提出的融合决策算法的识别准确率表现最佳，识别能力较单一的模型有较好的改善，特别是使用NPGFCC特征的融合决策ivector说话人识别系统，噪声环境下的整体识别率较其他算法有明显的提升，说明了结合NPGFCC特征的融合决策模型在说话人识别方面的有效性。

7 结束语

由于现实应用环境中噪声的存在，一定程度上制约了说话人识别技术的发展。本文通过结合人耳听觉特性，提出了一种抗噪性能良好的语音特征NPGFCC。该特征基于压缩归一化Gammachirp滤波器组，可以准确表征出语音段信号，并通过利用分段非线性幂函数变换增强其抗噪性能。实验证明，将本文算法应用在说话人身份识别方面，能够有效提升日常噪声环境中的识别准确率，且相对其他特征算法，NPGFCC有着最优的性能表现。另外，在识别模型方面，通过对i-vector+PLDA模型进行优化改进，在不增加算法复杂度的前提下有效降低了识别误差，改善了说话人识别系统在噪声环境下的抗噪鲁棒性问题。