圆弧青霉发酵右旋糖酐酶过程动力学模型的建立
黄瑞杰,蓝平,钟磊,覃琴,蓝丽红,韦佳蔓,廖安平,李媚
(广西民族大学 化学化工学院,广西多糖材料及改性重点实验室(广西民族大学),广西 南宁,530006)
右旋糖酐酶(dextranase)是由微生物产生用来降解右旋糖酐中的α-1,6糖苷键,使右旋糖酐链缩短、分子质量降低的酶类[1]。内切型的右旋糖酐酶随机水解右旋糖酐的α-1,6糖苷键,水解产物主要是异麦芽糖、异麦芽三糖和低聚异麦芽糖以及系列中低分子质量的多糖[2]。内切型的右旋糖酐酶在食品、医药、化工领域有着广泛的应用[3-5]。右旋糖酐酶法可取代传统的酸解法降解右旋糖酐,降低能耗、减轻污染,得到均一性好、杂质少的特定分子质量的右旋糖酐产品[6]。在诸多右旋糖酐酶产生菌中,青霉菌来源的右旋糖酐酶酶活力高、温度耐受性好、pH适用范围宽[7-8],青霉菌类右旋糖酐酶具有极高的应用价值。国内外对于菌体发酵右旋糖酐酶的研究主要集中在菌种筛选[9]、发酵培养基[10]和培养条件[11-12]的优化、右旋糖酐酶的纯化[13-14]和酶学性质[15-17]等方面,对菌体发酵过程动力学的研究和报道较少[18]。本实验在前期对圆弧青霉发酵产右旋糖酐酶发酵条件优化的基础上,对发酵过程动力学进行研究。考察发酵过程中菌体质量浓度、右旋糖酐酶酶活以及总糖(底物)质量浓度随时间的变化,选择适当的动力学模型对发酵过程进行拟合,获得圆弧青霉发酵过程动力学模型,并对此模型进行误差分析,为圆弧青霉发酵产右旋糖酐酶发酵过程优化以及大型反应器设计提供理论依据。
1 材料与方法
1.1 材料与试剂
右旋糖酐T70(Mw≈70 kDa)(分析纯),damas-beta试剂公司;98%浓硫酸(分析纯),成都市科隆化学有限公司;蒽酮(分析纯),aladdin试剂公司;圆弧青霉(P.cyclopium,CICC-4022),中国工业微生物菌种保藏管理中心。
种子培养基(g/L):蔗糖30、NaNO33、KCl 0.5、 MgSO4·7H2O 0.5、FeSO4·7H2O 0.01、K2HPO41.0,pH 6.0~6.2;
产酶培养基(g/L):右旋糖酐30、酵母膏4、ρ(KCl)∶ρ(FeSO4·7H2O)=10∶1、K2HPO41.0, pH 6.0。
1.2 材料与仪器
LDZX-30FBS立式压力蒸汽灭菌器,上海申安医疗器械厂; LT-XT摇床,瑞士Kuhner AG;ACB-4A1垂直流超净工作台,新加坡艺思高科技有限公司;SZ-97自动三重二次蒸馏水蒸馏器,上海亚荣生化仪器厂;THS-15数控超级恒温槽,宁波天恒仪器厂;UV-4802H双光束紫外可见分光光度计,上海尤尼柯仪器有限公司;H1850R冷冻离心机,湖南湘仪实验室仪器开发有限公司。
1.3 实验方法
1.3.1 粗酶液制备
装液量60 mL、接种量3%、培养温度30 ℃、初始pH 6.0、摇床转速160 r/min的条件下恒温培养72 h。取发酵液于10 000 r/min,4 ℃离心20 min后,取上清液即得粗酶液,稀释数倍供酶活和总糖质量浓度测定使用。
1.3.2 菌体质量浓度的测定
用干重法测定菌体干重,将发酵液离心后抽滤得到菌体,用蒸馏水洗3次,于80 ℃的烘箱中烘干至恒重,用分析天平测定滤纸前后的质量差即为菌体干重m(g)。根据菌体质量与发酵液体积(60 mL)计算菌体质量浓度ρ(g/L),如公式(1):
(1)
1.3.3 右旋糖酐酶酶活测定
取1 mL质量浓度为30 g/L的右旋糖酐T70(0.02 mol/L, pH 5.0的醋酸盐缓冲液配制)预热后与1 mL稀释过的粗酶液混匀,置于50 ℃恒温水浴保温10 min,反应结束取1 mL反应液于25 mL的具塞试管中,加入1 mL DNS试剂后,沸水浴后冷却定容,在540 nm处测定吸光度值,以同等条件下沸水浴10 min 灭活的酶液作为对照,计算酶活,如公式(2)所示。右旋糖酐酶的酶活用水解底物产生的还原糖的量来表示。右旋糖酐酶酶活力定义为:在pH 5.0、50 ℃,每小时水解右旋糖酐T70释放出1 mg还原糖(葡萄糖当量)为1个酶活单位(U)[19]。
右旋糖酐酶活/(U·mL-1)=
(2)
1.3.4 总糖质量浓度的测定
采用蒽酮硫酸法测总糖质量浓度[20]。
1.3.5 发酵过程曲线的绘制
进行圆弧青霉的发酵培养,从接种时起,每隔8 h取样,采用1.3.2、1.3.3、1.3.4的方法进行圆弧青霉菌体质量浓度、右旋糖酐酶酶活和右旋糖酐的质量浓度的测定,分别得到圆弧青霉菌体生长、右旋糖酐酶生成和总糖消耗的试验数据。采用Origin 8.0软件制作圆弧青霉发酵右旋糖酐酶的过程曲线。
1.3.6 发酵动力学模型的建立
1.3.6.1 菌体生长动力学模型的建立
微生物发酵动力学模型有Monod方程,Tessier方程,Contois方程,Moser方程和Logistic方程[21]。采用Logistic方程建立菌体生长动力学模型表示圆弧青霉菌体质量浓度与时间的关系。Logistic方程如公式(3):
(3)
式中:X表示菌体质量浓度,g/L;μmax表示最大比生长速率,h-1; Xmax表示最大菌体质量浓度,g/L;t为发酵时间,h。
当t=0时,X=X0,X0(g/L)为初始菌体质量浓度,对公式(3)积分得公式(4):
(4)
1.3.6.2 右旋糖酐酶生成动力学模型的建立
选用Leudeking-Piret方程来拟合菌体产酶的过程。
Leudeking-Piret方程为公式(5):
(5)
式中:P为右旋糖酐酶酶活,U/mL;α为与菌体生长率相关的产物合成参数;β是非伴随菌体生长相关的产物合成参数。
产物合成与菌体生长有偶联型、部分偶联型、非偶联型。α≠0,β=0,产物与菌体生长属于生长偶联型;α=0,β≠0,为非生长偶联型;α≠0,β≠0,为部分生长偶联型[22]。当产菌体生长于产物生成是偶联型时,α≠0,β=0。
将公式(3)带入公式(5)得公式(6):
(6)
将公式(6)积分得公式(7)。
(7)
1.3.6.3 右旋糖酐消耗动力学模型的建立
选用类Leudeking-Piret方程用来描述发酵过程中底物消耗的过程。
类Leudeking-Piret方程如公式(8):
(8)
式中:S为发酵液中总糖质量浓度,g/L;m为维持菌体新陈代谢因数,s-1;YX/S为相对于底物消耗的菌体得率系数;YP/S为相对于底物消耗的产物得率系数。
碳源消耗主要用于菌体生长和右旋糖酐酶的诱导合成时,用来维持细胞生理活动所需消耗的底物较小,可以忽略[23],即m=0。右旋糖酐消耗动力学模型可表示为公式(9):
(9)
式中:k1代表用于菌体生长的底物消耗常数,k2代表用于产物形成的底物消耗常数。
将公式(9)积分得公式(10):
(10)
式中,S0为发酵液中总糖初始质量浓度,g/L。
2 结果与分析
2.1 圆弧青霉发酵过程研究
按照1.3.5方法得到发酵过程中圆弧青霉生长、右旋糖酐酶生成以及右旋糖酐消耗的曲线,如图1所示。
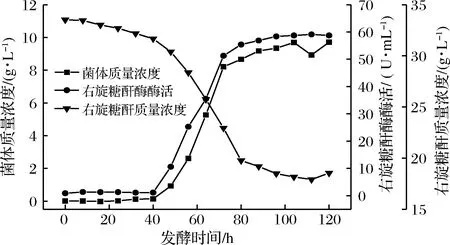
图1 菌体质量浓度、右旋糖酐酶酶活、右旋糖酐质量浓度随时间的变化Fig.1 Changes of cell mass concentration, dextranase activity and dextran mass concentration with time
由图1可知,接种初期圆弧青霉菌(CICC-4022)生长缓慢,随后生长速率逐渐增大,最后趋于稳定。0~40 h处于生长延滞期,圆弧青霉菌在这一时期生长速度较慢,几乎不产右旋糖酐酶,底物消耗的较少;40~72 h处于对数生长期,圆弧青霉菌体繁殖速度加快,菌体质量浓度增加,右旋糖酐酶大量产生,底物被大量消耗;发酵72~120 h,圆弧青霉菌的生长进入稳定期,菌体繁殖缓慢并逐渐呈现死亡状态,右旋糖酐酶合成速度减慢,圆弧青霉质量浓度和右旋糖酐酶都处于相对平衡状态,变化较小。由图1可知产酶和菌体生长密切相关,基本同步,说明圆弧青霉(CICC-4022)发酵右旋糖酐酶的过程属于生长偶联型。
2.2 圆弧青霉生长动力学模型
由图1可知,圆弧青霉的生长曲线接近于S型曲线,Logistic方程是一个典型的S型方程[24-25], Logistic方程适用于拟合圆弧青霉的生长过程。
Logistic方程的积分式为公式(4)。式中X0=0.003 3 g/L。 根据实验数据,用Origin 8.0拟合得出参数值;μmax=0.128 3 h-1,Xmax=9.551 7 g/L。
圆弧青霉生长动力学模型为公式(11):
(11)
2.3 右旋糖酐酶生成动力学模型
选用Leudeking-Piret方程来拟合菌体产酶的过程。由图1可知,圆弧青霉发酵过程中,右旋糖酐酶的生成与菌体生长基本同步,因此圆弧青霉发酵产右旋糖酐酶的过程属于生长偶联型,α≠0,β=0。
Leudeking-Piret方程的积分式为公式(7)。式中X0=0.003 3 g/L,μmax=0.128 3 h-1,Xmax=9.551 7 g/L。根据实验数据,用Origin 8.0拟合得出参数值,α=6.325 1。
圆弧青霉发酵产右旋糖酐酶的动力学模型为公式(12):
(12)
2.4 右旋糖酐消耗动力学模型
右旋糖酐是圆弧青霉发酵过程中的唯一碳源,主要用于维持细胞生长、菌体新陈代谢和诱导产物的合成[24]。通过菌体发酵过程中的底物消耗曲线可知,类Leudeking-Piret方程可以用来描述发酵过程中底物消耗的过程。发酵动力学参数如表1所示。
类Leudeking-Piret方程的积分式为公式(10)。式中S0=33.269 6 g/L,X0=0.003 3 g/L,μmax=0.128 3 h-1,Xmax=9.551 7 g/L,α=6.325 1,根据实验数据,用Origin 8.0拟合的出参数:k1=1.186 8,k2=0.056 8。
发酵过程中底物消耗动力学模型为公式(13):
(13)
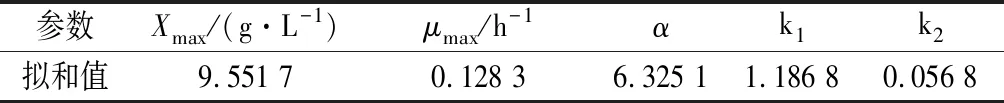
表1 发酵动力学模型参数Table 1 Parameter values in kinetic models of fermentation
2.5 拟合曲线分析
根据发酵过程中菌体生长、右旋糖酐酶生成和底物消耗的动力学模型,应用Origin 8.0得到圆弧青霉发酵过程中的动力学模型拟合曲线,结果如图2~图4所示。

图2 菌体生长动力学模型拟合曲线Fig.2 Cell growth kinetics model fitting curve
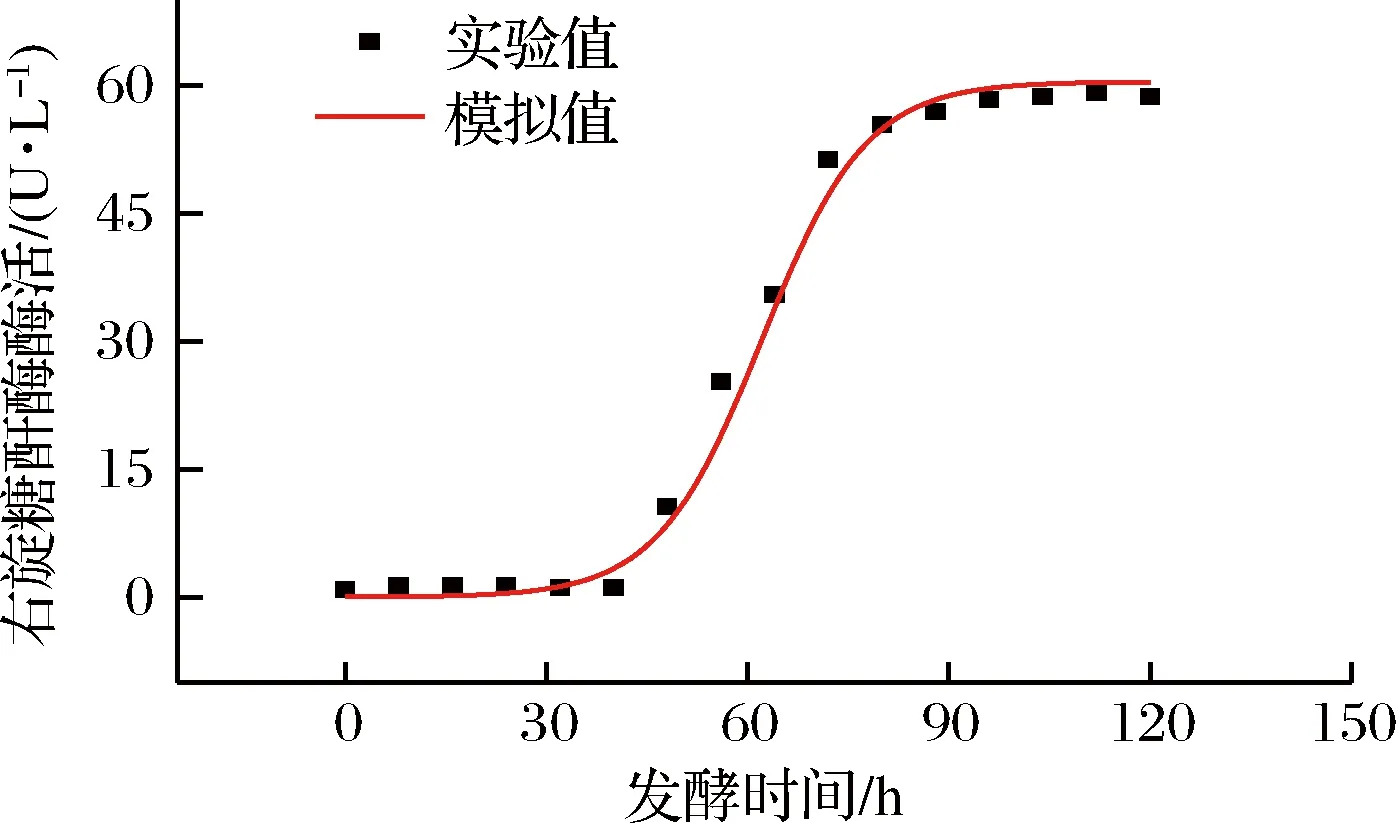
图3 右旋糖酐酶生成动力学模型拟合曲线Fig.3 Dxtranase production kinetics model fitting curve
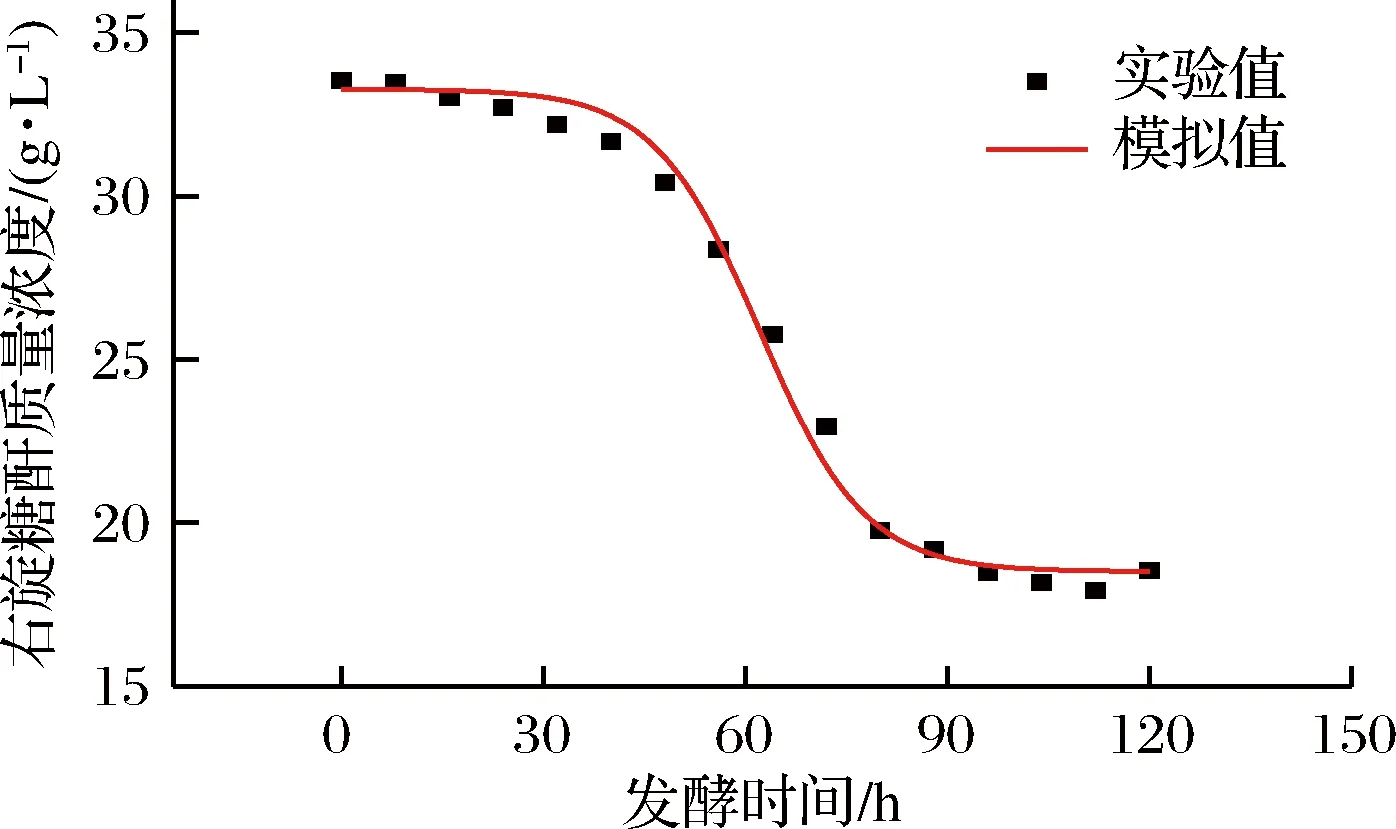
图4 底物消耗动力学模型拟合曲线Fig.4 Dextran consumption kinetic mobel fitting curve
菌体质量浓度、右旋糖酐酶酶活和总糖质量浓度的实测值、计算值相对误差如表2所示。
图2~图4分别为圆弧青霉生长、右旋糖酐酶生成和底物消耗的动力学模型的拟合曲线,菌体生长动力学、右旋糖酐酶生成动力学和底物消耗动力学模型拟合度相关系数R2分别为0.994、0.992、0.991,说明这3个动力学模型可很好地反映菌体生长、右旋糖酐酶生成和底物消耗的过程。
由表2可知,40 h之前菌体质量浓度和右旋糖酐酶酶活相对误差较大,基本>20%,可能是因为菌体处于生长停滞期,菌体质量浓度和右旋糖酐酶酶活数值上较小,造成较大的实验测量误差[23-24];40 h之后,菌体生长进入对数期,菌体质量浓度与右旋糖酐酶活逐渐增大,测量误差较小,相对误差随之减小,实验数据拟合较好。发酵过程中总糖消耗相对误差全部<7%,拟合良好,主要是因为总糖在研究的发酵过程中消耗较少,测量误差较小。总的来说,发酵过程中的3条曲线可以较好地反映圆弧青霉的生长、右旋糖酐酶的产生和总糖消耗的规律。
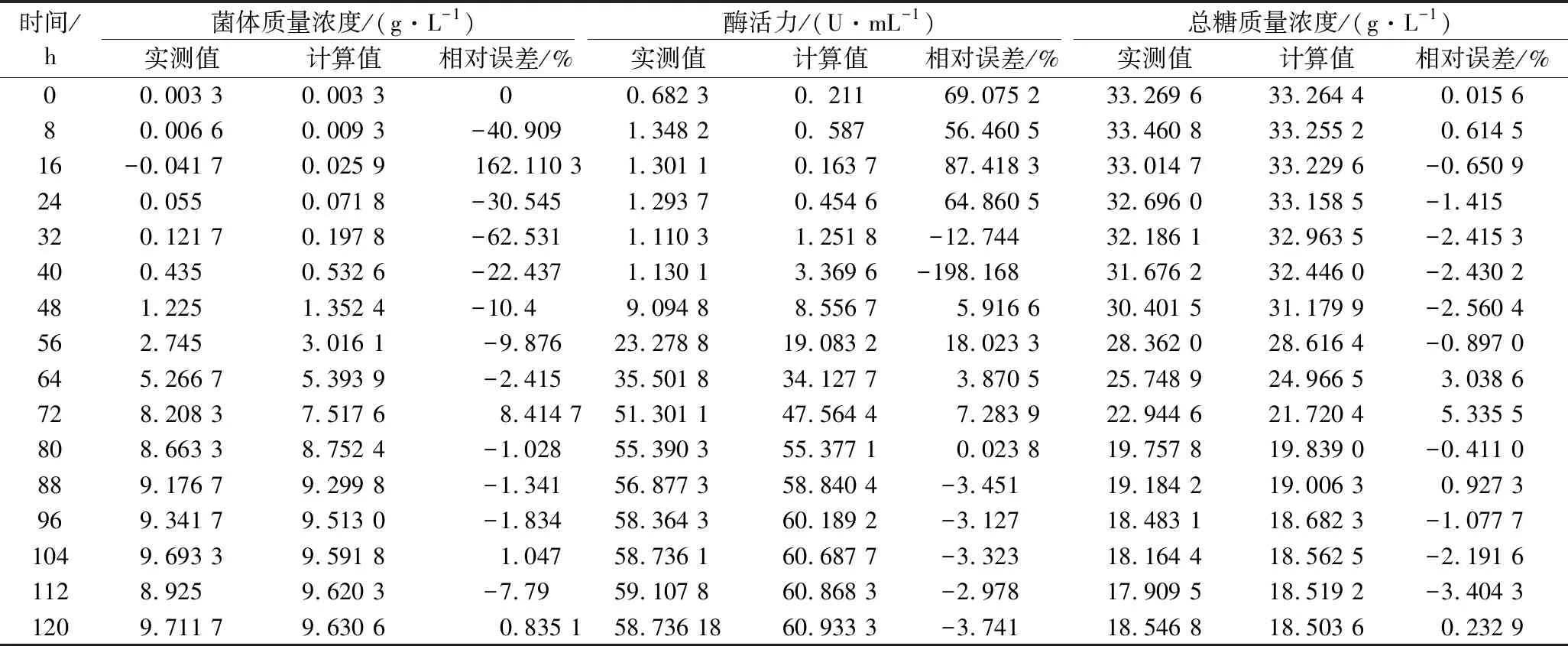
表2 菌体质量浓度、酶活、总糖质量浓度实测值与计算值的比较Table 2 Comparison between experimental and predicted values of cell mass concentration,dextranase activity,total sugar mass concentration
3 结论
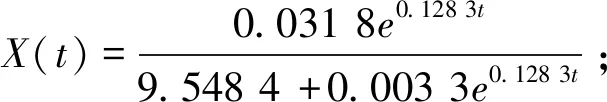
通过以上动力学研究可以看出,圆弧青霉菌的比生长速率、右旋糖酐酶的比生成速率在整个发酵反应过程是随时间变化的,圆弧青霉的比生长速率的最大值和右旋糖酐酶比生成速率的最大值均出现在菌体由延滞期向对数生长期的过渡期。在实际生产中,可以结合该试验得出的动力学模型对生产进行监控,并可以考虑在菌体生长对数期添加营养物质,提高右旋糖酐酶的产量,提高生产效率。

