正项函数项级数一致收敛的Gauss 指标判别法
王 瑜, 钟粤敏
(闽南师范大学数学与统计学院,福建漳州363000)
函数项级数是表示函数的一种重要方法,它的一致收敛性是研究函数项级数所确定的函数的分析性质(连续性、可微性、可积性等)的核心,熟知判别函数项级数的一致收敛性的判别法有魏尔斯特拉斯(Weierstrass)判别法(M-判别法)、阿贝尔(Abel)判别法、狄利克雷(Dirichlet)判别法等,它们是判别函数项级数的一致收敛性的有效方法.针对函数项级数所具有的特别情况,如一般项的正项的函数项级数,文献[1]按照正项级数收敛性判别法给出了正项的函数项级数一致收敛性的比值型判别法、 根式型判别法和Raabe 型判别法等.文献[2]给正项级数收敛性Gauss 指标判别法,它是比值判别型法、根式型判别法和Raabe 型判别法的推广,本文把它应用于正项的函数项级数的一致收敛性的判别,给出了正项的函数项级数一致收敛的Gauss 型判别法,它是已有的比值型判别法和Raabe 型判别法等一般化.
1 相关概念
函数项级数及其一致收敛的定义,可参见文献[1].这里我们仅给出与函数项级数一致收敛性判别的相关概念.为了叙述方便,已有的结论用引理给出.
函数项级数一致收敛的充要条件(柯西准则).
引理1[1]设函数项级数∑un(x)在数集E 上一致收敛的充要条件是

引理1 有如下等价的叙述
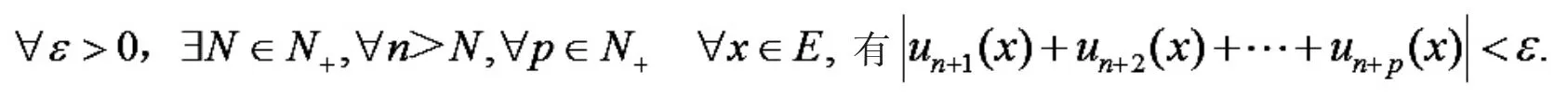
函数项级数一致收敛的充分条件(优级数判别法).
引理2[1]设有函数项级数∑un(x),若且正项级数∑Mn收敛,则函数项级数∑un(x)在数集E 上一致收敛.
正项级数的Gauss 判别法与Gauss 指标判别法.
引理3[2]如果正项级数∑an满足条件:,其中与 μ 是常数,而 θn是有界量,即,使得 θnL,则当>1 或=1, μ >1 时,正项级数∑an收敛;当<1 或=1, μ1时,正项级数∑an发散.
引理4[3]设有正项级数∑an,为正数列{an}的 Gauss 指标.则当 G >1 或G=+∞ 时,∑an收敛;当 G <1 或 G=-∞ 时,∑an发散.
2 主要结果及其证明
我们把正项级数的Gauss 指标判别法,应用于判别正项函数级数的一致收敛性,给出如下的定理.
定理 1 设∑an是在数集 E 上的正项函数项级数(an(x)>0,x∈E,n∈N+),
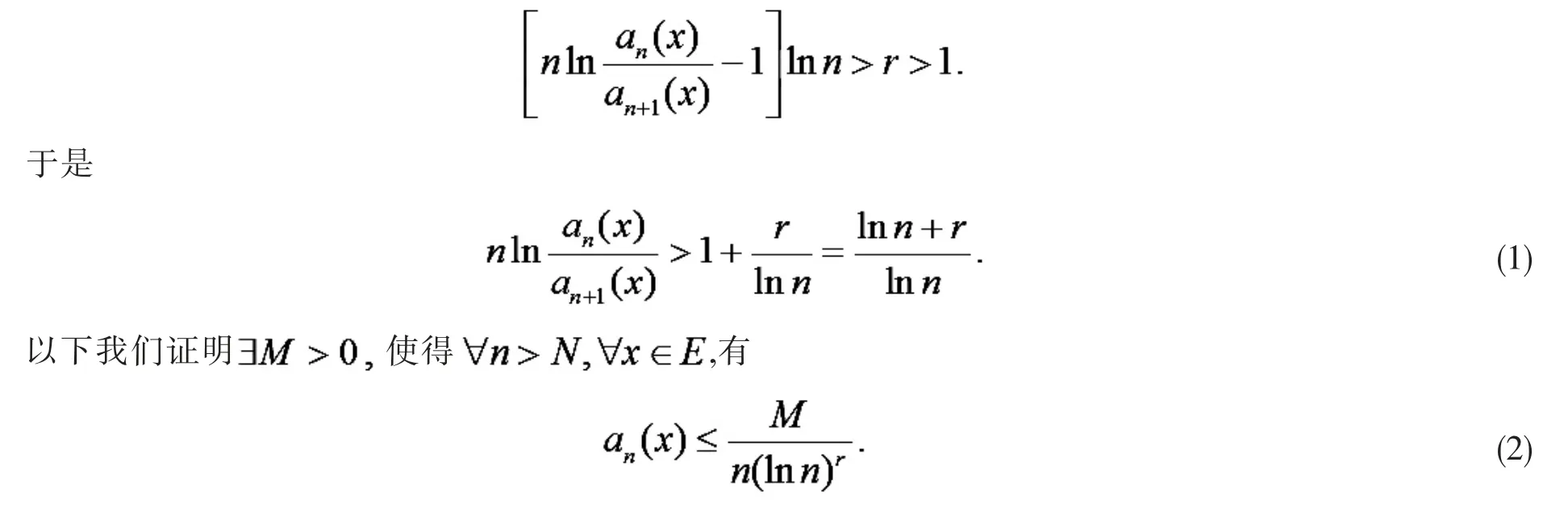


推论 1 设∑an(x)是在数集 E 上的任意函数项级数(an(x)≠0,x∈E),如果

且 an(x)在 E 上是一致有界,则∑ an(x) 在 E 上一致收敛.
根据定理1,我们可以得到[4]中正项函数项级数一致收敛的比值型判别法.
推论 2[4]设∑un(x)是在数集D 上的正项函数项级数,令,如果=q<1,并且 un(x)在 D 上是一致有界的,那么∑un(x)在 D 上是一致收敛的.

因而
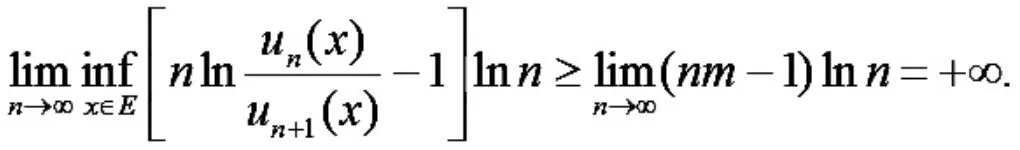
根据定理1,∑un(x)在 D 上是一致收敛的.
于是

所以
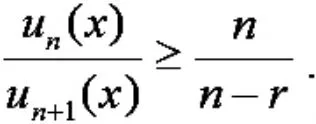
于是根据定理1,∑un(x)在D 上是一致收敛的.
我们给出[5]中的正项函数项级数一致收敛的Raabe 判别法.
推论 3[5]设∑un(x)为定义在区间 I 上的正函数项级数(an(x)≠0,x∈I),且{an(x)}在 I 上是一致有界的,存在正整数N0及常数r.
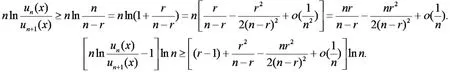
由于 r >1,有
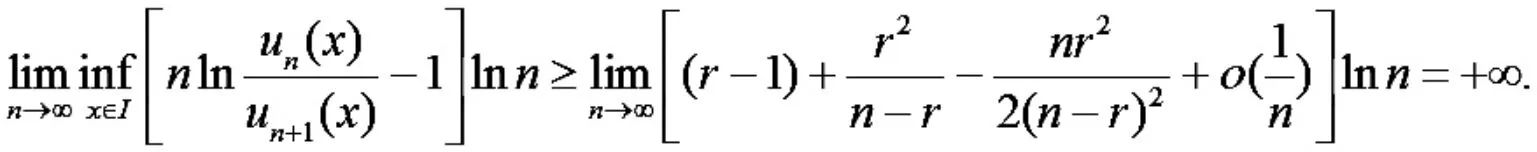
根据定理1,∑un(x)在区间I 上是一致收敛的.
3 应用举例
例1 设 f(x)为[a,b]上的正值连续函数,证明函数项级数
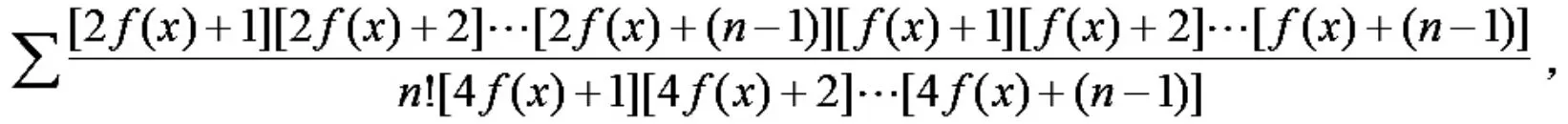
在[a,b]上是一致收敛.
解令
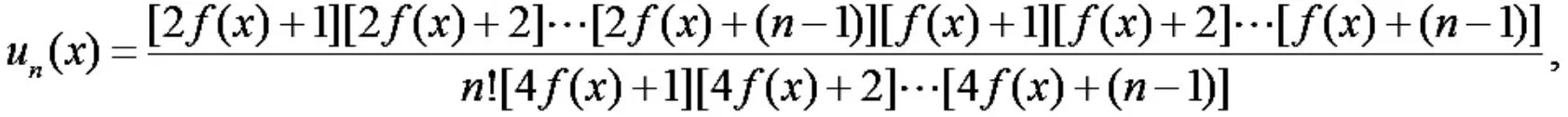
则有
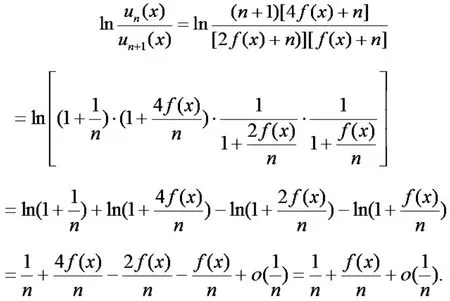
因为 f(x)为[a,b]上的正值连续函数,根据闭区间上连续函数的性质,函数 f(x)在[a,b]上有最小值,记其为 m 且 m>0.所以

于是

根据定理1,函数项级数
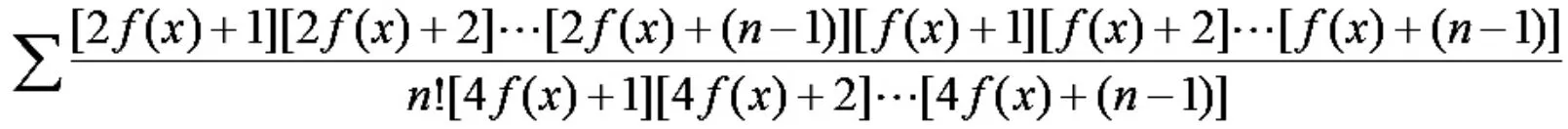
在[a,b]上是一致收敛.
说明 文献[4]中判别法(本文推论2)不能判定该正项函数项级数在[a,b]上的一致收敛性.事实上,对于n∈N+及x∈[a,b],有
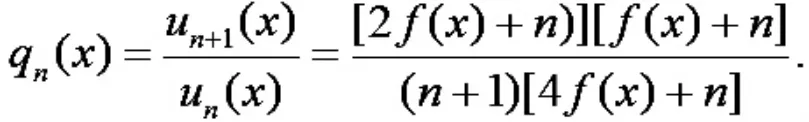
于是