二元土质深基坑支护体系设计研究

■ 广东华南建筑设计施工图审查中心有限公司 曾金祥

随着城市的快速发展，土地供应日趋紧张。为了充分利用有限的土地资源，城市建筑物不断向上下发展，地面上的建筑物越建越高，地面以下也是越挖越深。地下工程建设需要进行基坑支护，由于地质条件复杂、多变，地基、土质往往变化较大。以往基坑深度不大，深度范围基本处于土层中，个别进入岩层，也不太深，基坑支护设计均按一元土层考虑，存在以下三种可能破坏的形态。

1.半月弧滑移破坏

如图1所示。

图1

其验算公式为：

Mp—被动土压力及支点力对桩底的倾覆弯矩

Ma—主动土压力对桩底的倾覆力矩

Kov—安全系数 1.25

2.抗倾覆（踢脚破坏）稳定验算

如图2所示。

图2

其验算公式为：

Mep—被动区抗倾覆作用力矩总和

Mea—主动区倾覆作用力矩总和

Kt—抗倾覆稳定安全系数1.25

3.抗隆起破坏验算

如图3所示。

图3

其验算公式为：

抗隆起稳定安全系数Ks＞Kb=1.80。

以上是对支护三种可能存在的主要失稳状态进行的复核验算，作为一元土质，其失稳状态主要包括以上几种。一元土层基坑支护设计有多种方法，都比较成熟。

随着地下深度的增加，在较深的基坑中，出现“上层为黏土层、下层为岩层”的现象，其压缩性、稳定性、结构性均完全不同，称为二元土层结构，如图4所示。在二元土质结构中，基坑支护采用桩锚支护，其支护方案如图5所示，桩底嵌入下层基岩内一定深度。基坑以基岩为稳定支挡继续深挖几米甚至十几米，从坑底往上看，支护桩与吊脚相似，所以称为吊脚桩。

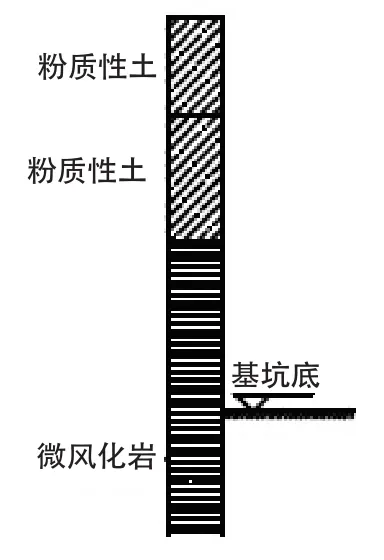
图4

图5

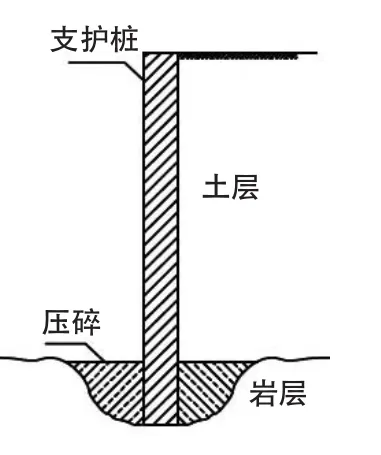
图6

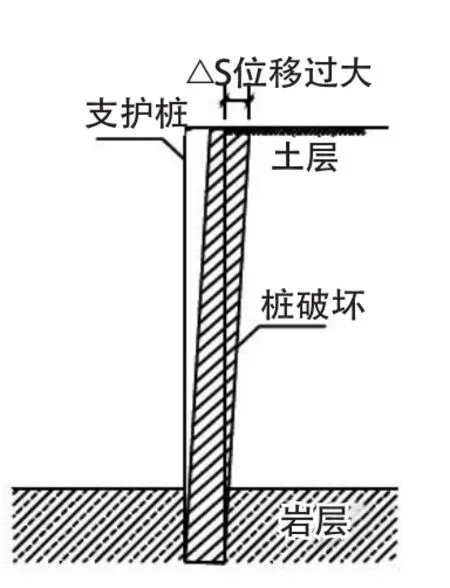
图7

图8

通常情况下，吊脚桩可能出现以下四种失稳状态：第一种是桩入岩深度不足，如图5所示，因此，设计要求入完整岩深度不少于500mm；第二种状态是桩身强度不足或刚度不足、顶点位移过大，如图6所示，在设计时往往增加锚杆；第三种状态是基岩局部风化严重、强度不足或空隙发育、迎土面发生隆起，如图7所示，顶点位移过大，需要增加锚杆；第四种状态是保留肩宽太小或肩宽岩受到破坏，如图8所示、肩宽坍塌、吊脚桩失稳，需要增加锚杆。

在二元土质结构吊脚桩支护体系中，有两个因素起关键作用：第一个因素是吊脚桩如岩深度，统计表明，总体趋向是桩入岩越深，支护顶部位移越小。但当桩入岩深度达到一定程度后，位移会趋于一个定值，理论上，支护桩入岩越深，基坑支护越安全。但由于设备能力所限，加上造价和施工工期的制约，并不是越深越好。根据多项工程统计，入岩深度0.5～1.5倍桩径最能反映支护顶点的位移变化。由于嵌固要求，桩进入岩层不少于0.5倍桩径，此时顶点位移最大，随着入岩越深，位移逐渐减少，当到达1.5倍桩径的深度时，位移开始趋于稳定，由于岩质自然离散性，个别岩可能达到2倍桩径后才会趋于稳定；另一个因素是支护桩与基坑边之间的岩厚，或称岩肩，一般吊脚桩的桩底嵌固力是由预留的桩肩来承受。理论上，肩宽越大越有利（图9），但由于在实际工程中地下室边线到用地红线间空间不会太多，因此，肩宽都不会太宽。统计表明，支护顶点位移与肩宽有关，肩宽越厚、位移越少。对于硬质微风化岩，当肩宽大于2倍桩径时，顶点位移影响甚微。在实际工程中，除了施工面需要外，往往留给肩宽剩下500mm ～1000mm左右，为了保证支护体系的稳定，往往需要在桩底部岩肩顶部加设一道锚杆，以抵抗桩脚力。

图9

由于在二元土层吊脚桩基坑支护设计时，常用方法主要是传统的“m”法和边坡设计法，但两种方法都较为粗糙，“m”法中岩层的m值在不同的工况下会发生变化，目前条件下，要准确得出各工况下的m值是不现实。边坡设计法是把上部土层和支护桩作为外加荷载，计算岩层边坡的稳定和位移，忽略了支护桩在不同工况下对下部岩层的影响。在目前设备条件和经济、工期要求下，吊脚桩基坑支护设计确实是较为理想的解决方案。

研究发现，对二元土质采用吊脚桩基坑支护设计，可以得出如下几个结论：

（1）支护桩不必深入基坑底部，利用基岩高强、致密和稳定性，减少支护桩长度和入岩深度，降低造价。

（2）可以大大缩短施工周期。

（3）受力相对较明确，施工过程基坑安全可控。

（4）计算分析，上下层合算和上下分开的计算方法，均可满足目前的工程需要。

（5）岩层的强度和完整性对支护稳定至关重要。

（6）吊脚桩入岩深度与位移成反比关系，但进入一定深度后趋于稳定。

（7）开挖过程中预留肩宽及肩宽的完整性很重要。

4.结语

随着城市的发展及土地资源的紧缺，再加上对停车位的需求越来越大，多层地下室的需求变得越来越大。因此，建筑物的地下基坑也会变得越来越深。如何保障施工期间基坑的安全、缩短工期、节省投资，是摆在设计者面前的重要问题。根据现场条件和地质条件，选择合适、合理的支护方案，无论是对工期、还是对投资，都变得越来越关键。